Track Processing Approach for Bearing-Only Target Tracking

Published Online October 2009 in MECS

The bearing-only target tracking using passive sensor means to obtain target motion element through angle-only measurement. Even if the target motion is constant velocity, namely CV, the target motion is very difficult to express by using linear equation in the θ - φ (azimuth and pitching) plane. This problem is high nonlinear in substance and target motion takes on higher maneuverability in polar plane. As yet, resolving method of this issue has been difficult in maneuvering target tracking domain [1-5]. Traditional multi-station joint passive tracking watching system estimates 3D information based on 2D measurement. Namely, this system indirectly gets the target position information by

Manuscript received January 16, 2009; revised June 21, 2009; accepted July 12, 2009.

using multi-angle crossing approach [6,7]. But this approach brings more “ghosting” so that great computation cost is produced in target association tracking because of sensor measuring error itself. At the same time, this approach is limited by distance demand between the station and the other station. Thus, the target tracking error is enlarged and application value of this approach is little. In view of the demands of the concealment and flexibility for passive tracking system, the suited target tracking algorithm based on single passive sensor is urgent very much. In correlative references[8,9], some scholar make linear assumption for bearing-only target motion if sampling time of passive sensor is shorter and target confirming accuracy is high enough. Based on this assumption, azimuth angle and pitching angle of target is regarded as decoupling. From its inspiration, Aiming at the bearing-only tracking characteristics, a resolving approach completely based on angle-only measurements is studied by the deeply analysis of data association, association gate technology and multi-model filtering approach in this paper.

• II.    Track initiation based on bearing-only

MEASUREMENTS

• A. Existing problem and solution

Multi-target track initiation is primary problem of maneuvering target tracking. It is a decision-making link of new target file establishment. For multi-target tracking processing, the right track initiation is key to reduce the burden of track processing and improve maneuvering target tracking effect. Traditional track initiation approach is difficult to find real target quickly and effectively. Taking into account the relevant characteristics of single passive tracking system and high real-time demand in the battlefield, mostly maneuvering target tracking need feedback target track information timely for tracking with scanning system. So taking sequential processing approach, which including heuristic algorithm and logic-based algorithm [10-13], is primary choice for track initiation in the bearing-only tracking system due to good real-time performance. It is worth noting that heuristic algorithm has high false track probability for simple heuristic rule. For high confirming efficiency and excellent performance, logic-based algorithm is widely adopted in real engineering application. This paper presents bearing-only track initiation approach based on traditional logic-based algorithm. It is depicted as

• 1)    Isolated bearing-only measurement is used to establish new candidate track. By angular velocity rule that will be depicted as association gate design in part ^ , measurements in next cycle are put into association decision.

• 2)    Candidate track from step 1 is linearly extrapolated. Regard extrapolative point as associated center and make association decision for bearing-only measurements from next cycle. If some candidate track isn’t associated with every measurement, those candidate tracks are terminated.

• 3)    For every candidate track including three or more measurements, it is extrapolated by using second-order polynomial. Then make relevant associated decision according to the extrapolative point. The rest can be deduced up to the N-th step by analogy. Confirm target track by comparing the relation between innovation and threshold at last. For time k(k=N) , bearing-only measurement sequence corresponding to candidate track m is

^{ z\, p (1, m ) , z 2, p (2, m ) ,"^., z N , p ( N , m ) ^}

where p (k, m) is depicted as measurement number corresponding to temporary track m .

Define cumulative innovation as

N

J ^{( m} ) = ^ ' [ ^zk , p ( k , m ) ^zk , m ] ⁽ R k ) [ z k , p ( k , m ) ^zk , m ] ^k = 1                                                   (2)

where zˆk,m is position estimation of candidate track through polynomial fitting, namely nx z k,m = £ am( kAT )j/ j!                            (3)

j = 0

where a ˆ ^m _j is polynomial fitting coefficient.

Proved in reference [14], statistical value J* (m) is chi-square ( %2 ) distribution with Nnz - nx degree of freedom ( nx is polynomial fitting order) . If statistical value J * (m) satisfy test of threshold у, which is gotten based on % distribution with Nnz freedom, namely

J * ( m ) <  у

- n_x degree of

Then, this candidate track is target track. It turn into tracking phase. For quick track initiation, this paper set continuous decision cycle as 4.

• A.    Nearest Neighbor Data Association (NNDA )

NNDA [15,16] is a early simple association algorithm. It helps to ensure the real-time demand of passive sensor target tracking. This approach associates the nearest neighbor measurement away from the tracking target in statistical view. This statistical distance is defined as weighed norm of innovation vector’s , that is dk = zTr iSк zkkIk-1                                 (5)

k k I k-1 k where zk|k-1 is filter innovation, Sk is innovation covariance matrix, dk2 is norm of error vector.

The radical meaning of NNDA is uniquely choosing the nearest measurement away from target as associated object to estimate target state. For easy realization and little computing cost, it is applied to the tracking systems which have the high SNR and the little target density. But when the measurement density is tremendous or multitarget association gate intercrossing each other, the nearest measurement not always come from the tracking target. Therefore, NNDA’s anti-jamming capability is not so good and this approach easily brings false association.

• B.    Joint Probabilistic Data Association(JPDA)

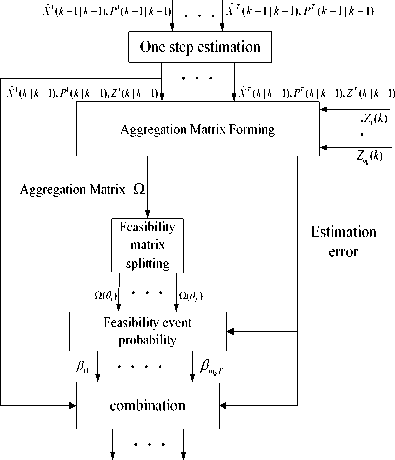
JPDA [17-19] is advancing extending algorithm from PDA [20] (Probabilistic Data Association). It resolves the bug of false tracking in the application of PDA algorithm in the high maneuvering target density environment. This algorithm always is considered as one of the most perfect association approach. But comparatively, its computing cost is high because the association hypothesis event number between target and measurement is exponential expanded. Moreover, the distance between the two targets is very near. It is possible to bring bias and aggregation of track. Flow chart of this algorithm is shown in figure 1. The key technology of this algorithm lists the following

• 1)    Association gate

  -----------—----------< g 2 [ z - ) ^t ( k I k - 1)] S' ( k ) ^{- 1} [ z - z ^t ( k I k - 1)]'     ‘

Where, t=1,2,^,N, Zt ( kIk - 1) is the position estimation

A t ( k ) -

of target t at k; St (k) is error covariance matrix of the measurement t at k.

• III. Feasibility study of bearing-only data

ASSOCIATION ALGORITHM

X ^ˆ1( k | k ), P ¹( k | k )           X ^{ˆ T} ( k | k ), P^T ( k | k )

Figure 1． JPDA algorithm flow chart

0 jt = { valid measurement Zj ( k ) comes from the target t }

where j=1, …, m _k , t=1,2,…,N.

When t =0, 0 j 0 denotes measurement Zj ( k ) coming from clutter or noise. Note association event posterior probability

P jt = P { 0 jt\Z^k }                         (11)

Β jt is association probability. It is probability of association event appearance.

Define joint association event

mk

⁰ = I ⁰ jtj j = 1    ^j

Joint association event θ may represent matrix:

0( 0 ) =[< & jt ( 0 ) ]                             (13)

where

О .,(0) = jt

⁰ jt ⁰

or else

S ( k ) = E { [ z - z t ( k | k - 1)][ z - z t ( k | k - 1)]' }

(7) where g_t ² denotes gate value.

If and only if the target measurement involves in the target association gate, it is regarded as valid measurement, or rejected. Assume that there are m_k valid measurements involving in N target-gates. Those measurements in the association gate are regarded as following association standby.

2) Clustering matrix

If consider that clustering matrix (or confirmed matrix) have m_k rows and N ＋ 1 lines, clustering is defined as the most aggregate of conjoint tracking gate. All of targets are divided into different groups according to different clustering. There is a binary element matrix of clustering matrix which associates each of these groups all the time. Clustering matrix is defined as follows:

ⁿ= ( ® jt ), j = 1,2,..., mk ; t = 0,1,..., N                      (8)

where C jt denotes that measurement j whether or not is contained by association gate.

If satisfying two conditions as follows, joint association is defined as feasibility event θ :

• Every measurement only comes from a headspring, target or clutter, namely:

T тj (0)=I cojt (0)=1     j =1,2,...,mk              (15)

t = 0

• Every target only has a measurement, that is

mk

For feasibility event 0 , corresponding matrix П ( 0 ) is referred to as feasibility matrix. It is gotten by splitting clustering matrix , that is scanning Q and only choosing a “1” in every row as feasibility matrix element. Except for the first line, every line of feasibility matrix only has a “1”. S t ( 0 ) is defined as target detecting indicator and т j ( 0 ) is defined as measurement indicator. Then clutter

number is:

mk

Ф ( 0 ) = I [1 - т j ( 0 )] j = 1

If Z_j ( k ) is in the association gate or else

where j = 1,2,..., m, , t = 1,2,..., N , and t=0 means that k no target exist and correspondingly all line elements of Q are 1. In this time, any measurement originates from clutter or falsehood.

3) Feasibility Event

Feasibility event is produced by clustering matrix. Assume association event

• 4)    Feasibility Event Probability and Association

Probability Calculation

The sum of joint association event is L at k . Condition Probability, that is

• • If clutter model is Poisson distribution, then

^{ф ф m}k          T

P( 0 i\Z^k )=— П [ Nt , ( Zj ( k ))] ^т j П ( pD ) ^S t (1 - pD )1 ^{S t (18)} c j = 1    ^j             t = 1

• Else if clutter model is uniformity distribution,

then

mkT

P(θi|Zk)=1Φ!∏[Nt(Zj(k))]τj ∏(PDt)δt(1-PDt)1-δt c vΦ j=1jt

Where, c and c’ are unitary element.

Ntj (Zj(k))=N(Zj(k);Ztj(k|k-1),Stj(k))

Where, N denotes normal distribution.

Finally, association probability is:

L βjt=∑P{θi|Zk}ωˆjt(θi)

i = 1

Where, j = 1,..., m_k ; t = 1,..., T

The probability of invalid measurement originating from target t is:

mk

β _{0 t} = 1 - ∑ β _jt , j = 1,..., m_k ; t = 1,..., T (22)

j = 1

5) State Estimation m_k

X ^{ˆ t} ( k | k ) = ∑ β jt X ^{ˆ t} j ( k | k )

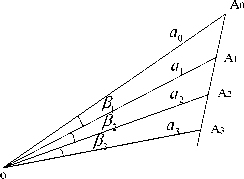
Fig ure 2． Angle change of target motion

Combining with the angle change analysis of bearing-only target motion, the gate of extrapolating by using linearly and second-order polynomial will be presented. As shown in figure 2, suppose that observation point is O and target moves along A0A3 as straight line. The sample points of the moving target at every sample time are A0,A1,A2,A3... and the distances of the different sample points away from observation point are a0, a1, a2, a3  The angles between observation point and the sample points areβ1,β2,β3  With a view to the

IV. Association gate Design for bearing-only

TARGET TRACKING

Gate technology is a key for data association. It affects the computing complexity of data association. Moreover, it decides the efficiency and performance of data association. The traditional gate technology is inefficient in θ - φ plane. They not only can not limit false track overextension with the dense clutter but also hardly confirm those real target tracks.

Firstly, initial gate will be design to confirm isolated measurement. There are two ordinary initial gate technologies. One is χ2 test method, the other is based on utmost velocity as v ∈ [v,v]. For the reason of k min max complicated 2D bearing-only target motion as high nonlinear, the traditional gate technology is inefficiency. So gate technology in θ-φ plane must be based on the characteristic of bearing-only target motion. Obviously, target motion is nearer, angle measurement change is larger. Thus, the area of confirming measurement must have good adaptability. In view of these factors, rational gate design is core for track processing in bearing-only tracking. Under normal circumstances, tracking system require that target will be reliably tracked at Dmin kilometers away from observation point. Design initial gate as the rule

assumption that sampling time of passive sensor is shorter and target confirming accuracy is high enough, so the average velocity of adjacent sampling circle is approximately equal and target motion is an approximately straight line form. Simultaneity, angle change in θ - ϕ plane is small. If supposing that A ₂

corresponds to the sampling time k, equations are established based on triangular relationship according to figure 2 . Simplify those equations and get result as

Δ t_k ^k _- ^{- 1} ₂ ⋅ a _{2 =} sin β _{1 ≈} β ₁

Δ t_k ^k _{- 2} ⋅ a ₁sin( β 1 + β 2 )   β 1 + β 2

where Δ t_i ^j denotes time interval between sample

time i and sample time j . Then

( β 2

β 1 k -

^Δ t k^k -2

k -1

_k      Δ t_k ^k _{- 2}

⋅Δ t k -1 ) ≈ [ _{Δ tk} k _--1 ₂

⋅

a ₁

a ₂

-

Δ t k^k -1

_Δ t_k k _--1 ₂

- 1] ⋅ β 1

D min          ^Δ t k^k - 1

_k - _{k - 1} - 1) ⋅ β 1

D min ^- v max ^⋅Δ t k -1 ^Δ t k -2

Formula 26 denotes the upper limit of angle deviation when candidate track is linearly extrapolated in θ - ϕ plane. Use the upper limit as linearly extrapolating

association gate in the course of track initiation. Make the assumption that measurement z _i ( k ) and the j-th component of vector z ˆ _m ^L ( k ) which is gotten by extrapolating candidate track m . If satisfying the following formula, measurement z _i ( k ) will be confirmed.

zi(k+1)-zj(k) ≤    vmax tk+1 -tk        Dmin *103

z i , j ( k )

-

ˆ ^L m , j

k

where t_k is k-th sample time.

( k ) ≤ ( ^{Δ t k k}k ^-- 1² ⋅ ^Δ t k - 2

( z k -1, i ^- z k -2, i )

k - 2

D - min

D min ^- v max ^⋅Δ t k^k - 1

Δ t k^k

-

^Δ t k^k - ¹2

- 1) 0

When extrapolating candidate track using second-order polynomial, suppose that A ₃ corresponds to the sampling time k . Then, equations are established based on triangular relationship. Simplify those equations and get result as

^A t k -2 ^a3 =    sin ^P 2 ^P 2

A t kk -2 a 2 "sin( P 2 + P 3 )~ P 2 + P 3

Then

P 2      P 1

о U ^P 2 ₊ Л _tk -1 ^A tk -2 ^A tk -3 x kA

^P 3 ^{- [(}TTT ^{+ A} t k -2 Th---- ) ' ^A t k -1 ⁺

^A 4-2            ^A 4 -3

P 2      P l

^A t k -2 ^A t k -3 / k.k \2 _ / ^a 2 ' ^A t k -2 _ ^A t k -1 _ ^A t k -1

k -1        ' ^{( A} tk ^- 1 ) ] ⁽       .,k -1     _A,k -1     _A,k -1

^A t k -3                       ^a 3 ' ^A t k -2 ^A t k -2 ^A t k -3

(Atkk-1)2 - 1)- R + Atkk-1 -Atk- + (Atkk-1)2 - R a tk-1 -a tk -1       2        a tk- -a tk :2        1

k 2 k 3                         k 3 k 3

A t k - 2	D mm	A t k - 1	A t k - 1	( A t k - 1 )2      1)
" A tk - 1 A t k - 2	D min - V max . A t k - 1	k - 1 A t k - 2	A tkk - 3	Д k - 1 Д k - 1     ) A t k - 2 - A t k - 3

, A t kk - 1 -a t k - + ( A t kk - 1 )² A t k - ^- 3 -A t—

- P 1

Formula 28 denotes the upper limit of angle deviation when candidate track is extrapolated in 0 - ф plane using second-order polynomial. Use the upper limit as second-order extrapolating association gate in the course of track initiation. If satisfying the following formula, measurement will be confirmed.

1, j ( k ) ^- z m , j ( k )| ^

A t

A t k -l

( A t k -1 )² a t k - ^- 2 -a t k - ^- 3

^- 1) ^{- (} z k -1,

^- z k -2, i ) ⁺

A t k -1 -A t k - ^- 2 + ( A t k -1 )²

^{- (} z k -2, i    z k -3, i )

A tV- 1

-a t kk - ₃ ²

where z ˆ _m ^R _{, j} ( k ) is the j-th component of vector z ˆ _m ^R ( k ) which is gotten by extrapolating candidate track m using second-order polynomial. These gate technologies make full advantage of the characteristic of bearing-only target motion and association gate adaptively adjust according to the measurements of the different candidate track.

• V.  Bearing-only tracking algorithm based on

interactive multi-model(IMM)

A ． Multi-model algorithm introduction

In the course of study and engineering application of bearing-only maneuvering target tracking, the tracking performance of single model based adaptive filter isn’t so good. Its limitation mainly is the competition between tracking accuracy and rapid response to target tracking. Especially to bearing-only tracking, for its higher target maneuverability and the variety of structure and parameter existing in target motion model, single-model adaptive filter is difficult to accurately recognize these varieties in time so that inaccurate model and false tracking appear.

Multi-model filter use several suited model to approximate the real target motion. Among them each model has a potential maneuvering mode. Random maneuvering of target is depicted as random hopping among models. By designing filter composed of several model, accordingly carry them into effectively execution for maneuvering target tracking. Thus, improving tracking performance is naturally shown. If making assumption that random hopping of target motion model state is discrete and target motion state is continuous, maneuvering target tracking is typical mixed estimation issue. Traditional solution of mixed estimation issue is combining estimation with decision-making. If making hard decision for the uncertain parameter and structure, the estimation result is usually bipolar optimization rather than global optimization. Under the circumstances, multi-model approach becomes mainly solution to mixed estimation nowadays.

The basic idea of multi-model maneuvering target tracking approach is mapping potential motion model into model set. Each model in set represents different maneuvering mode and varieties of models based filter works in parallel. State estimation output is Bayesian illation based data fusion of all filtering state estimations. Suppose that i e {1,2,....,(M_s ) ^k } is model state sequence index up to time k and M_s is model number in model set. Simultaneity, ^{x ˆ} i ( k | k ) and Pi ( k | k ) respectively is state estimation and error covariance under assumption of model state sequence _m ^k matching model sequence m_i^k of i index. P { m^k = mk | zk } is posterior probability of this assumption. S^k is a set of all potential model sequence. _Z ^k is measurement sequence. Then, optimal multi-model estimation under LMSE need to considered all potential model state sequence assumption, namely

<

"x(k I k) = ^ xl (k I k)P{mk = mi I Zk } mk eSk

P( k | k ) = ^ { P i ( k | k + ( x ( k | k ) - .x i ( k | k ))( x ( k | k ) - .x i ( k | k )) ' } P { 5 k = m k | z k } m k e S k

Apparently, the number of potential model sequence assumption presents an index growth with time flowing. It produces an unacceptable computation cost. Especially to the disadvantage that target threatening degree can’t be estimated for distance information lack in passive tracking system, so real-time is very important to this system. Thus, the computation cost of selective approach must satisfy the demand of tracking operation. IMM algorithm [21-23] proposed by H.A.P.Bolm is an inferior optimized multi-model algorithm which has high cost-effective. This algorithm makes assumption that transformation of different model obeys finite Markov chain of known transition probability. It has the same performance as GBP2 and advantage of computation cost as GBP1. IMM is regarded as the first multi-model algorithm up to application value[24].

B. IMM algorithm based on bearing-only measurement

In polar coordinate, redefine state variable as х = [ е ф е ф ]‘                         (31)

Assume that target motion can be depicted as a model from r assumption model in some time, note model set Mr : = { 1,...,r } . The effective event of model j is noted as Mj ( k ) in sampling period ( tk - 1, tk ] . For the assumption model j , whose target state equation is

X ( k ) = FJ ( k - 1) X ( k - 1) + GJ ( k - 1) Wj ( k - 1)

<

. z ( k ) = H ( k ) x ( k ) + v^j ( k )

Assume that probability of model j ц j (0)=Pr{ Mj (0)}

Transition probability

Pij =Pr{ Mj (k )\Mi (k-1)}

It is known and decided by Markov chain from Mj ( k - 1) to Mj ( k ) in this time.

• 1)    Mixed probability calculating

If M ^j ( k ) and measurement set

Zk - 1 ( Zk - 1: = ^{ Z ⁽¹⁾, Z ⁽²⁾,..., Z ^{( k - 1)}} ) is known in sampling time k , appearance probability of _M ⁱ can be expressed as

^ ( k - 1| k - 1) = P { M ( k - 1) = Mi\M ( k ) = Mj , Z_k - 1 } =— pjui ( k - 1) cj

Where, i,j =1,2,…,n, c _j is normalization constant.

Where, function distribution is Gauss.

• 3)    Renewing model probability

Each renewing model probability lists as follows

1n uj(k)=-Aj(k) S PijU1 (k-1)                      (38)

^c        i = 1

• 4)    State and covariance estimation.

Formula of State and covariance estimation is

n

J T ( k\k ) = S2 X j ( k\k ) u-( k )

,                      i = i

P ( k \ k ) = jb u j ' ( k ) { P j ' ( k \ k ) + [ XZ ¹ ( k\k ) - X( k I k )][ jX^J ( k \ k ) - X( k I k )]'} 1 = 1

By analysis of algorithm framework, measurement information utilization of IMM exists in not only filtering estimation but also model probability. And IMM can adaptively adjust model by model probability change. Simultaneity, this algorithm has modularization characteristic. Through different application, filtering module can adopt all kinds of linear and nonlinear filtering algorithm. Finally, efficiency is improved in virtue of each filtering module working side by side in this algorithm.

C ． Model selection for bearing-only tracking

In this paper, model selection only limits to CV and CA because there isn’t so good performance for CT in polar coordinate and value of ω is difficult to grasp. The research indicates that common motion can be approximated by certain combination of CV and CA.

• VI.    Simulation

For getting more clear result, track initiation will be simulated firstly in order to test its distinguishing ability and fast ability in clutter environment. At last, set environment to test the final effect of track processing system as a whole.

A . T r a c k initiation simualtion

Introduce guide line for simulation judgment [25].

• 1)    False probability of track initiation (FP)

NN

FP = S f i / S n i                 (40)

i = 1         i = 1

where N is simulation number based on MonteCarlo. N =30 in this paper. f _i is false track number and n _i is initiated track number as a simulation.

• 2)    Correct initiation probability ( C )

N

S l ij

Cj =

N

where l _ij represents if target j is initiated correctly in the i-th Monte-Carlo simulation. Correct is 1, or 0.

TABLE I.      I nitial states of the targets in C artesian

COORDINATE

Target	Process noise coefficient	Model	Velocity	X	Y	Z
1	0.70	CV	980	15000	5100	5000
2	0.90	CA	520	10000	1200	1000
3	0.60	CV	500	12000	100	-800
4	1.25	CA	430	9500	6000	200
5	1.00	CV	480	10000	800	-600
6	0.70	CV	550	9000	-2500	1000
7	0.50	CV	530	15000	8000	-600

-100

-200

-300

-600       -400       -200         0        200       400        600

Azimuth /mrad

Figure 4 ． Effect of track initiations

There are seven targets in simulation environment. Their movements are CA and CV respectively. Process noise is white Gaussian noise. Initial states of the targets list as table 1 (position and velocity unit are m and m/s respectively.). There, acceleration of target 2 and target 4 are 75m/s² and 87m/s² respectively. Figure out bearing-only measurement in polar( θ - φ ) coordinate based on these target tracks in Cartesian coordinate. Assume clutter density 2 = 6.25*10 - 5 /mrad² (Clutter number is Poisson distribution. Clutter is scattered as uniform distribution. ) and measurement noise coefficient is 1.5mrad. Note that angle unit is one thousandth of radian, namely mrad. There, D min =10km, T =1.5s, v _max =1km/s, a _max =100m/s² and threshold test significance level a = 0.01. In order to test speed of track initiation, this simulation is based on 6 sample cycle. Typical clutter environment is shown in figure 3. Effect of track initiation is shown in figure 4. Based on 30 times MonteCarlo simulation, false track probability with different clutter density is shown in figure 5 . Correct track initiation probabilities of the targets as follow

C 1 =86.7%, C 2 =83.3%, C 3 =93.3%, C 4 =80.0%, C 5 =80.0%, C 6 =90.0%, C 7 =93.3%.

1     1.5     2     2.5     3     3.5     4     4.5     5     5.5     6

clutter density ^{(10 -5 / mrad2)}

Figure 5 ． False track probabilities based on the clutter density

E

-100

-200

-300

^ ++

A

-400

-600       -400

-200

A

200       400       600

+ Clutter target

Azimuth (mrad)

□ Real measurement of

B. The tracking effect based on JPDA-IMM for maneuvering target

Here, a selective maneuvering target is shown in figure 6 and figure 7. The performance comparison of IMM and single model approach based on JPDA algorithm is shown in figure 8 and figure 9 based on Monte Carlo simulation. Where, make assumption that T =1.5s, sampling number N =350.

Assume that measurement noise is Gauss white noise whose coefficient is 1 mrad. In this tracking filtering algorithm, the approach of direct angle modeling is chosen. In the single model algorithm, tracking model is CV whose state noise coefficient is 0.7 mrad. Simultaneity, there is an IMM filter composed of 4 model used to track. These models are depicted as: There are different Q matrix for model 1-model 3, which is CV whose state noise coefficient respectively are 1, 0.1, 0.01 and model 4 is chosen as CA whose state noise coefficient respectively is 0.1. Initial model probability matrix и = [1/4 1/4 1/4 1/4]

Model transition probability matrix

Figure 3 ． Bearings-only measurements in clutter environment

0.97	0.01	0.01	0.01
0.01	0.97	0.01	0.01
0.01	0.01	0.97	0.01
0.01	0.01	0.01	0.97

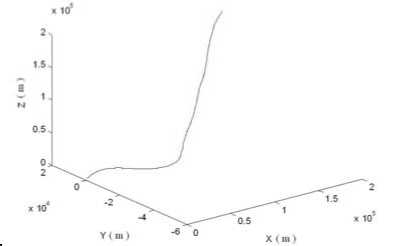
Figure 6. Target track in Cartesian coordinate

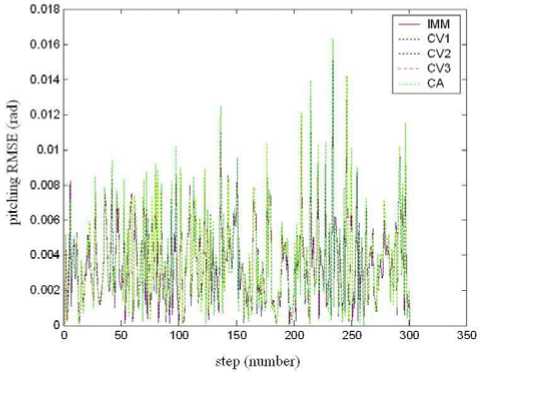
Figure 9. Pitching RMSE comparison of IMM and single model

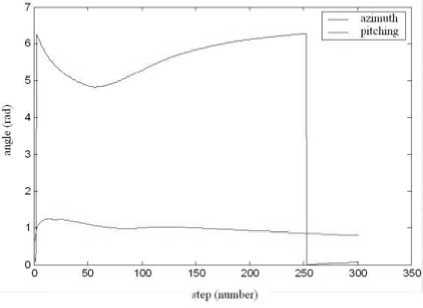
Figure 7. Target track in bearing-only coordinate

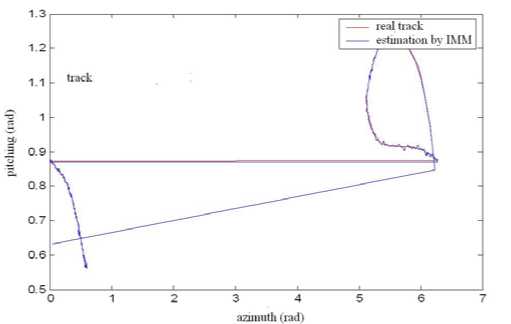
Figure 10. Tracking effect in bearing-only coordinate

In these simulation figures, tracking comparison of IMM and every model of composing IMM are given in polar coordinate. Paying more attention to the dimension, horizontal and vertical axis, respectively, are radian and RMSE. Simulation time cost is shown in Table 2.

azimuth RMSE (rad)

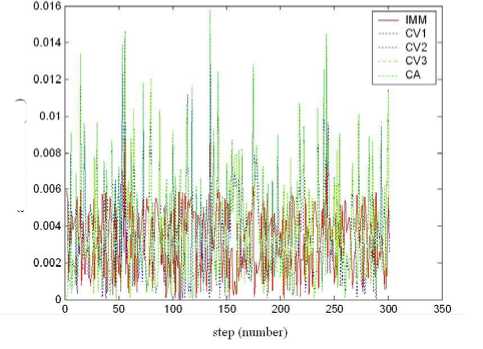
Figure 8. Azimuth RMSE comparison of IMM and single model

TABLE II.    Computation cost comparison of IMM and single model for target 1

Model	IMM	CV1	CV2	CV3	CA
Time(s)	1.0940	0.2350	0.2030	0.2180	0.2500

• VII.    conclusion

Simulation of track initiation approach in this paper shows that its confirming efficiency is effectively improved based on the presented gate technology. This approach effectively affirms the correct probability of track initiation for maneuvering target. According to simulation result of whole track processing system and application of actual ship-borne infrared system, adopting JPDA as data association is suitable for bearing-only tracking system using passive sensor. Whereas, its performance takes on not so good comparing with performance in Cartesian coordinate. Moreover, JPDA is very high need for target detecting probability, sampling time and clutter density etc. Unsuitable value might lead to missing tracking. There is also clear conclusion that tracking accuracy is improved by using IMM. On the other hand, algorithm complexity is enhanced in deed, and that computation cost is in direct proportion to model number. Under the accuracy condition satisfied, model number choice is less as possible. By simulation, draw a conclusion: if the model number of CV exceeds 3 or number of CA exceeds 2, minimal performance improvement is displayed in the bearing-only tracking with computation cost greatly increase. It is the reason that too much unnecessary model competition in the multi-model data fusion. Excessive use of the model, not only increase computation cost but also reduce the accuracy of estimation. Based on simulation and outdoor actual debug of ship-based defense system, balancing the two factors that accuracy and computation cost, that choose the two CV and one CA to compose of multimodel tracking filter can get the more satisfied results.