Траектории лучей в радиально-градиентной среде

Автор: Курушина С.Е., Максимов В.В., Ратис Ю.Л.

Журнал: Компьютерная оптика @computer-optics

Рубрика: Численные методы компьютерной оптики

Статья в выпуске: 22, 2001 года.

Бесплатный доступ

Аналитические решения лучевого уравнения получены для радиально - градиентной среды с профилем показателя преломления, ограниченным членами четвертой и шестой степени расстояния от оптической оси в разложении показателя преломления в ряд.

Короткий адрес: https://sciup.org/14058497

IDR: 14058497

Текст научной статьи Траектории лучей в радиально-градиентной среде

Для анализа оптических систем, содержащих элементы с радиально-градиентным профилем показателя преломления, необходимо знать представленное в аналитическом виде уравнение траектории луча, распространяющегося в такой среде.

Один из возможных способов аналитического решения лучевого уравнения состоит в представлении траектории луча в виде разложения по степеням расстояния z , измеренного вдоль оси симметрии профиля показателя преломления. Полученные на этой основе формулы представлены в работе [1]. Недостаток этого способа заключается в том, что при практических расчетах бесконечные ряды заменяются конечными суммами, в результате чего ход луча рассчитывается приближенно.

Другой способ основан на методе последовательных приближений. Этот способ был применен в работах [2, 3, 4] к радиально-градиентным средам с положительной оптической силой, и обобщен в работе [5] на среды как с положительной, так и отрицательной оптическими силами.

В данной работе предложен метод определения траектории луча в цилиндрической системе координат, позволяющий для среды заданной оптической силы найти координаты произвольной точки луча р (расстояние от оптической оси) и ф (полярный угол) в зависимости от расстояния z , измеренного вдоль оси симметрии профиля показателя преломления.

n = n ₀ (1 - sign ( - n 1 ) T 1 р + T_XT ₂ р -

- sign ( - n ₁) т ₁ ⁶ т ₃ р ⁶ + ...), где

₂ 2 n 1

^T 1 =-----

^т 2 =

^т 3 =

n ₀

- ^f1 +

ⁿ 2 ⁿ 0

2 2

n 2 J

n ₀4 n ₁ ²

ⁿ 2

₊ n ₃ n ₀ n ₁

Ход луча будем описывать в цилиндрической полярной системе координат, ось Oz которой совпа-

дает с осью симметрии распределения показателя преломления.

Учитывая, что показатель преломления зависит только от координаты р , в выбранной системе координат лучевое уравнения принимает вид [6]

d ds

f do dф n -Л— e + р—~ e

V ds ^р ds ^ф

+— e z ds

=~r^e р , (5) а р

где e _р , е _ф , e z - единичные орты цилиндрической полярной системы координат. После преобразований [6] это уравнение можно представить в виде системы двух уравнений для компонент р и ф

Постановка задачи

Для среды с радиально-градиентным распределением показателя преломления его профиль определяется выражением:

а р dz

аф ар

eA n ² ( ^р ) - ^в

2 А ¹/²

z ²

р ² J

n = Z n k р 2 k , к = 0

где р - расстояние от оптической оси системы. Тогда с учетом р ⁶ :

n = n о - sign ( - n 1 ) n 1 р ² + n ₂ р ⁴ + n 3 р ⁶ + ... (2)

Здесь

sign ⁽-

' 1, ( n ! < 0 )

n 1 ) = 1 0,( n i = 0)

- 1, ( n 1 > 0 )

Если первый коэффициент радиального градиента n₁< 0 , то среда обладает положительной оптической силой.

Квадрат показателя преломления может быть представлен в виде:

Р -Чр) - в

2 V1/2

z ²

р ² J

где величины

P z = n ⁽ р ^)cos Y = n ⁽ P о ^)cos / 0 ₍₇₎

Р ф = n ⁽ р ) ^ sin у ^cos ^ф = n ⁽ р 0^ р 0 sin / 0 cos ^ф 0 ⁽ являются инвариантами в радиально-градиентной среде. Углы у и ф показаны на рис. 1. Величина P z представляет собой оптический направляющий косинус луча относительно оси Oz.

Точка входа луча в неоднородную среду характеризуется величинами р ₀ и ф ₀ .

Таким образом, задача определения траектории луча, распространяющегося в радиально-градиентной среде с профилем показателя преломления, ограниченным членами четвертой и шестой степени расстояния от оптической оси в разложении показателя преломления в ряд, сводится к решению системы дифференциальных уравнений (6) с учетом выражения (4) при заданных начальных условиях.

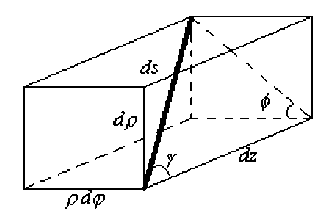
Рис. 1. Разложение элемента длины луча на компоненты

Решение дифференциального уравнения (12) зависит от вида корней уравнения n ³ + Р П + 1 = о . Дискриминант этого уравнения D определяется выражением [9]:

D = f p 1 + ¹ 1 =

I 3 J 1 2 J

= ( n о² - P z ²)² [ 4 т 2 ( n о²

4*27 n _о ⁶ т 1² т 4

P z ²) - n о² I

. (14)

Анализ траекторий лучей

1. Квадрат показателя преломления ограничен р Запишем первое из уравнений системы (6) для случая, когда n2 = n0(1 - sign-и1)т2 р2 + рт2р4): (8)

^d ^p ¹ . 2 „ 2 2 2 2,

= ~(nо - Pz - sign(-ni)nот1Р + dz Pz

24 4

+ n о т тг Р

22 2 22 2 2 2

₊ ⁿ о ^т 1 Р ф [ ²⁷ ^т 1 ^т 2 Р ф + ⁴ ⁿ о ± ¹⁸ ^т 2 ⁽ ⁿ о ^- 4*27 n 6 т 1² т 4

а) Кубическое уравнение имеет действительные корни , если D < о и p < 0 [9]. Положим

^в Ф ) 1/2 Р Р

R = ⁽ signq ) 4p\

3 . (15)

cos Y = —q—

2 R ³

Тогда действительные корни определяются выражениями [9]:

При n 1 >0 , когда среда обладает отрицательной оптической силой, - sign ( - n ₁) n 2 т 2 = n 2 т 2 , что далее в формулах соответствует верхнему знаку.

В случае n₁ < 0 среда обладает положительной оптической силой, - sign ( - n ₁) n 2 т 2 = - n 2 т 2 , что далее в формулах соответствует нижнему знаку.

После замены р ² = 5 получим

П ₁ = - 2 R cos—

/Г 2n)

n = -2R cosl

² L 3 3 J

' Y 4 n 1

n = -2 R cosl

3 ( 33

Для многочлена

d⁵- — 2 4 .3 ₊ 2 2.2

, = „ ( n 0 т1 т 2 5 ± n 0 т1 5 + dz Pz

+ ( n о² - P z *5 - Р ф ²) ^1/2

3 ± ¹ 5 2 + ⁽ ⁿ о P z ) 5 _ Рф

± 2 ⁵ 2 4 ⁵ 2 4

^т 1 ^т 2 ⁿ о ^т 1 ^т 2 ⁿ о ^т 1 ^т 2

действительные корни определяются следующим образом

Приведем кубический многочлен к каноническому виду

d5 = 2nот1 (53 ± 1

dz Pz

(n о - Р z 2 ) . _ РфХ1/2

2 _ 4 „ 52г n о т1 т 2 n о т1 т 2

и сделаем замену переменных [9]

П = 5 ± 1/3 т ² т ₂ ; d n = d 5 •

Для кубического многочлена получим приведенное выражение. Тогда

d n ² ⁿ о ^т \ 44 з 1/2

— =----„----- VI ⁺ Р П ⁺ q ) , (12)

dz Pz где

⁵ 1 = П 1 ⁺т^ = ^- ² ^R ^cosv⁺т^

3 т ₁ т ₂ 3 3 т ₁ т ₂

1 (Y1

52 = П2 + = -2 R Чт + 2П\ + Т^.

3 т ₁ т ₂ L 3 3 J 3 т ₁ т ₂

. _ _ 1 _ fY 4 п \_ 1

⁵ 3 = ⁿ 3 ⁺ = ^- ² ^R ^cos l ■ I ⁺ —2—

3 т ₁ т ₂ L 3 3 J 3 т ₁ т ₂

Обозначим наименьший из корней 5 через а , средний по величине - через р , а наибольший по величине - у . Тогда уравнение (11) можно переписать следующим образом:

d ⁵ = 2^442- (( 5 - « )( 5 - Ф ). 5 - Y F. (19)

dz P z

После разделения переменных получим:

³⁽ ⁿ о² ^- P z 2 ⁾ ^т 2 ^- ⁿ о²

³ ⁿ о ^т 1 ^т 2

2 2 2 22 2

± ² ⁿ о + ⁹ ^т 2 ⁽ ⁿ о ^- P z ) ^- ²⁷ ^т 1 ^т 2 Р ф

27 n о² т 6 т 22

________ d5 ________

4 ( 5 - а Х 5 - Р )( 5 - Y )

² ⁿ о ^т 12

P z

^т - 2

dz .

В левой части этого уравнения под знаком корня должна стоять положительная величина, т. е. выражение (17) должно быть > о. Это условие выполняется для интервалов:

1. а < 5 < в и

2. у < § .

Рассмотрим решения системы (6) для каждого из этих интервалов.

1. a < § < в .

Для решения уравнения (20) введем новую переменную ф по правилу [7]

При такой замене уравнение (20) приводится к виду (22) с модулем интеграла k , определенным в (23). Однако величины u и u 0 здесь определяются так

u ₀

= arcsin

P о² ^- Y

P о² - в

§ = a + ( в - a ) sin ² ф . (21)

г = arcsin

После несложных преобразований из уравнения (20) можно получить:

2 г dф 2 noт 4тх f / 0V 2 (z -z0),(22)

4 y - a г oV1 - k 2sin2 Ф

P ²

- Y

^- ^в

Решение уравнения (20) имеет теперь более сложный вид, чем (25):

Y - Р $п

ⁿ о ^т 1

4т 2 ⁽ Y ^- a )

где

P ²

P z

( z

^z о ⁺ ^z' )

k ² = ^{p a}

Y - a 0 < k ² < 1

cn ²

ⁿ о Г ² -J Т 2 ⁽ ^Y ^- ^a ) ,

------------------( ^z ^- ^z о ⁺ ^z )

Р z

u ₀ u

= arcsin

^p o - ^a в - a

arcsin

- a

В результате, после интегрирования выражения (22), получим:

Здесь z' имеет такой же вид, как в (24), но и₀ нужно брать из (28), cn в - эллиптическая функция Якоби, называемая косинусом амплитуды [8].

Зависимость полярного угла от расстояния от оптической оси определяется из второго уравнения системы (6) при помощи замены (27) и представляет собой комбинацию эллиптических интегралов первого и третьего рода:

ⁿ o^T\ 4^T 2⁽ Y ^- ^a ⁾ ₍

F ( ^г , ^k ) = ------------- ( ^z ^- ^z 0 ⁺ ^z )

z ,= P z F ( г o , k )

ⁿ 0 ^T 2 4^T 2⁽ Y ^- ^a ⁾

вф (n + 1) А ф = фо +-----2 / / П(г,n,k)- nnот1 -Т2 (Y - a)Y

РФ

. (30)

ⁿⁿ о ^т \ 4 ^т 2 ⁽ Y ^- ^a ) Y

F ( г , k ) + ф

В выражении (30) параметр интеграла n = - Py , величины и и и₀ определены в (28),

Здесь F ( u , k )- неполный нормальный эллиптический интеграл первого рода [8]. После обращения интеграла (24) окончательно получим:

p ² = a + ( P - a ) sn ²

ⁿ о ^т 1 4^T 2⁽ Y ^- ^a ⁾₍ „

--------------⁽ z - z o + z )

, (25)

sn в - эллиптическая функция Якоби, называемая синусом амплитуды [8].

Определим теперь зависимость полярного угла ф от расстояния p из второго уравнения системы (6). Проведя преобразования, аналогичные указанным выше, несложно получить следующее выражение:

ф = ф о +---- ₂ , ф [ П ( г , n , k ) -П ( г о , n , k ) ] ^,(26)

nот1 4Т2 (Y - aР где параметр интеграла n = Р—— , п(м, n, k) - не-a полный нормальный эллиптический интеграл в форме Лежандра третьего рода [8], остальные величины определены в (23).

2. Рассмотрим второй интервал у < § • В этом случае для решения уравнения (20) необходимо сделать замену переменных [7]

§ = y - в sin ² ф 1 - sin ² ф

вф (n + 1) A ф =--2 , , п(го , n, k) + nn о Tif 2 (Y - a )Y (31)

+------2 ^в ^ф, x F ( " о , k )

ⁿⁿ о ^Т 1 2 ⁽ Y ^- ^a ) Y

Таким образом, если многочлен (17) имеет дей- ствительные корни, то решениями системы уравнений (6) являются выражения (25,26) и (29,30).

б) Кубическое уравнение имеет два комплексных корня и один действительный , если D > о и p < 0 или p > 0 [9]. Корни приведенного многочлена третьей степени представлены в таблице 1.

Обозначим действительный корень многочлена (17)

§ 1 = П 1 +----- у = ^a .

3 т 2 т {

Тогда

, 3₊ 1 у 2 , ( n о ² -в z ²) , Р_Ф² ₌

S — 2 ^ ⁺ 2 4 ^ 2 4

Т 1 Т 2 n о Т 1 Т 2 n о Т 1 Т 2

= (^-а)(^2 + х^ + ст), где (^2 + %^ + ст) - трехчлен с вещественными коэффициентами всегда остается положительным при вещественных §. Коэффициенты с и % можно найти из таб. 1. Интервал a < § соответствует положи - тельным значениям выражения (17).

Таблица 1

p<0 и D>0

p>0

( signq ) p

R =--------

ch ^ =

2 R ³

( signq ) p

R =--------

sh T = -9—

2 R ³

Действительные корни

П 1 = —2 Rch —

, T П 1 = ^—2 ^Rsh у

Мнимые корни

T T

П ₂ = Rch — + i \3 Rsh —

T T

n = Rsh + i V3 Rch — ²3 3

n = Rch — — i V3 Rsh —

3_{3 3}

_ , T , T

П ₃ = Rsh у — i 73 Rch у

Чтобы проинтегрировать уравнения (6) введем новую переменную [7] по правилу:

S = а + Vа2 + %а + оtg2 ф. (32)

В результате после преобразований из уравнения (20) получим:

1 г d ф =

( а ² +ха+ст)¹⁴ u ₀ V 1 - к ² sin ² ф

в z

⁽ z ^— z 0 )

где

ф = ф0 + е(1—b) I1(и) + еР (и, к) — ф;

в ф

е =;

14 12

2n0т1^т2 (а + ха + о) (а — (а + ха + о) )

а + (а + ха + о)

b= ;

а — (а + ха+о)
I,(и) =——П(и,^,к | +
^1V ’ ь ² — 1 V ь ² — 1 J

1 , V1—b2A + к^к'2 + b2к2 sin и
+ln

2 ^(1—b2)(к '2 + b2 к2) [ V1—b2A — к^к '2 + b2 к2 sin и ф = е(1—b) I1 (и 0) + еР (и 0, к),

k ²

0 < к

(

1 ^—

< 1

а ■ х 2

A = 4 1 — к ² sin² и , к ' ² = 1 — к ².

и ₀ = 2 arcsin

________Р 2 —а

Р 0 - а + 4 (а2 + ха + ст )

Величины k, u, u₀ определены в (34).

Таким образом, если многочлен (17) имеет два комплексных корня и один действительный, то решением системы уравнений (6) являются выражения (35,36) с учетом (34).

и = 2 arcsin

Р ²

— а +

V (а2 + ха + ст)

2. Квадрат показателя преломления ограничен р⁶ Рассмотрим решения системы уравнений (6),

Далее, проинтегрировав уравнение (33), окончательно определим зависимость

если квадрат показателя преломления задан выражением (4).

Сделав замену переменных р ² = ^ , уравнения

(6) можно переписать так:

z — z 0 + z')]) + а,

d z = ² ⁿ0 4 ^T 4

dz P z

J^_ ^3

Ч ^T з

± 4- s2 +

^T 1 ^T 3

2 n от2 J^ (а2 +ха

о =----—----- в z z ,= в zF (и 0, к)

2 n 0т2 4^2 (а2 +хс

⁽ n 0 ^— ^p z ²⁾ г _ ^Р Ф \ 12

2 6 ^S 2 6 )

ⁿ 0 ^T 1 ^T 3 ⁿ 0 ^T 1 ^T 3

Ввиду громоздкости преобразований при определении зависимости полярного угла ф от р , здесь приведен окончательный результат:

|ф = P:_ (±^4+^3 ± ^2 + dS 2 n 0т1Цт 3 ^ т1т 3 T1T3

⁽ ⁿ 0 ^— P z ²⁾ К _ ^РФ A — 12

2 6 ^S 2 6 )

ⁿ 0 ^T 1 ^T 3 ⁿ 0 ^T 1 ^T 3

Решение системы уравнений (37) зависит от вида корней многочлена четвертой степени. Определим корни 5 -

Преобразуем многочлен четвертой степени к приведенному виду. Для этого введем переменную П = 5 ± т 2/ 4 Тх т 3 [9]. В результате получим

± 5 * + 2 53 ±

^Т 1 ^т 3

( n 2 - P z ) в ²

+ 2 6 5 - 2 6

n 0 ^Т 1 ^Т 3 n 0 ^Т 1 ^Т 3

= ±п * + рп2 + qn + r где р=

+ 3 т 2 ± 8 т ₃ 8 т * т 2

23 2 2 22

n 0 i.2 4-I 2 n о 1 3 TOl 3 ⁽ n о

8 n 0 т 1 т ₃

42 22 2 2 2232

т ^т 2 ^n о — IVL 2 n о I 3 tu^и+и 2 ^т 3 ( n о р z ) _)ит ^т 3 Р ф

256 n 2 т 8 т *

Вид решения уравнения

± п * + рп2 + qn + r = о зависит от вида решения его кубической резольвенты:

z ³ ± 2 pz ² + ( р ² + * r ) z - q ² - о. (*о)

Запишем для (40) приведенное уравнение:

у ³ + р'у + q' = о;

, + 12 r - р ²

^р = —3—^;

, = + 2 р ³ + 72 рг - 27 q²

q = ₂₇

При этом знаки перед радикалами z_i выбирают так, чтобы р/р/ = - q .

Если корни уравнения (40) действительны и положительны, то уравнение

± п ⁴ + р п ²+ q n + r = о (**)

имеет 4 действительных корня. Если (40) имеет положительный действительный и два отрицательных действительных корня, то (44) имеет две пары комплексно сопряженных корней. Если (40) имеет один действительный и два комплексно сопряженных корня, то (44) имеет два действительных и два комплексно сопряженных корня.

Для уравнения

± 5* + Т-5 ³ ±4- 5 ² + ⁽ n ^о2₂ ^- в ²⁾ 5 - 4^67- = о (45) ^Т 1 ^Т 3 ^Т 1 ^Т 3 n о ^Т 1 ^Т 3 n о ^Т 1 ^Т 3

2 корни определяются так: 5 i = Л г + т 2 / * Т 1 т 3 ( i =1,2,3,4 ).

В зависимости от коэффициента при старшем члене, вида корней 5 i и интервалов, на которых (38) > о, в таблице 2 приведены необходимые для решения системы (6) замены переменных [7] и полученные зависимости p (z) и ф ( р ) .

В таб. 2 используются следующие обозначения. Для случая, когда все корни многочлена (38) вещественны, эти корни обозначены: а , в , у , 5 , причем предполагается, что а < в < Y < 5 В случае, когда (38) имеет два вещественных и пару комплексных корней, у < 5 являются вещественными корнями, а комплексные корни заданы выражением b₀ ± i c o ( с₀ > 0 ). В случае, когда (38) имеет две пары комплексно сопряженных корней, эти корни имеют вид b i ± i C i ( C i > 0 ), b 2 ± i C 2 ( C 2 > 0 ), b i > b 2 .

Кроме того, в таб. 2 использованы вспомогательные величины:

Дискриминант приведенного уравнения для кубической резольвенты D = ( р' / 3 ) 3 + ( q' / 2 ) 2 . Если D <0 ир <0 , корни действительные и имеют вид:

_⁵ ^- ^b о Y ^- b о .

tg 0 1 = --------- , tg У 2 = -------- ^;

c ₀ c ₀

⁽ signq' ) Лр

R =---------- cos Т = -q-T-2R3

V у, = -2 R cos у,

'Т 2 л)

у 2 =^- 2 ^R cos l у + у I ,

V = tg

^- ⁰ 1

0 2 + 0 1

tg 0 3 = cT+CT , tg 0 * b ₁ - b ₂

^c 1 ^- ^c 2 _; b ₁ - b ₂

'Т *л) у 3 =- 2 R cos l у + у I ,

Если р' <0 и D '>0 или р' >0 корни могут быть определены из таб. 1 , в которой величины p и q нужно заменить на р' и q'.

z_{ = y i + 2 р / 3 - корни кубической резольвенты (40).

Приведенный многочлен четвертой степени в (38) имеет следующие корни [9]:

₉ 0 cos 0

tg ^{2 5} = ³

2 cos 0 *

Вид интеграла I₁(u) определен в (36).

Таблица 2 составлена с учетом работ [7, 8].

п 1 =⁽V z T ⁺ V z / ⁺ V z /) / 2;

п 2 =⁽V z T ^- V z / ^- V z /^)/2;

п 3 = (- V z T + V z / - V z /)/ 2;

п * = ( - V z / - V z / + V z /) / 2.

Заключение

В выражениях (25, 26), (29, 30), (35, 36) и таб. 2 представлены в аналитическом виде уравнения траекторий лучей, распространяющих в радиальноградиентной среде с профилем показателя преломления (4). Эти выражения имеют достаточно простой вид и могут быть легко разложены в ряд по заданному параметру.

С учетом формулы (7) полученные выражения дают возможность при любых начальных параметрах определить высоту и наклон луча в произвольной точке траектории.

Зависимости р (z) и ф (р) для профиля показателя преломления, заданного выражением (4)
Нули (38)	Коэфф. при старшем члене	Интервал	Замена переменных	Выражения для u , u₀, к², z ' , n; b ,с - вспомогательные величины	P (z), ф ( Р )
Четыре вещественных.	+1	^ < а или 8 <^	^ _ 8 ( у-а ) -у ( 8-а )&1П ф ( у-а ) - ( 8 - а ^П ф	■ /⁽ ^ро ^- ⁸ ⁾⁽у ^- а ) u_n _ arcsin —0---------- V ( Р о - Y )( 8 - а ) . /⁽ Р ² ^- ⁸ ⁾⁽ у ^- ^а ) u _ arcsin —z---------- У ( р ² - у )( 8 - а ) z' _----- з / ^P ^z F' ( u о , k ) n 0 Ч 4^T 3⁽ Y ^- ^а ⁾⁽ ⁸ ^- ^в ) k 2 _ ( 8 - а )( у - в ) ( Y - а )( 8 - в ) у ( а - 8 ) n _ 8 ( Y - а )	8 ( у - а ) - y ( 8 - а ) sn²о ² -	n ⁰ ^т 3, Н^у - ^а >( ⁸ - ^в > ₍_ , .) _ в ₂ ⁰ _
					^р - ( Y - а ) - ( 8 - а ) sn ² в ф Ф ^_ Ф 0 ⁺ ;. Г” ⁿ 0 ^т 1 ⁸Н^т 3 в ф ⁺₃ /---------------- ⁿ 0 ^Т 1 /4^Т 3⁽ Y ^- ^а ^)(с ^в ф ⁽ Y ^- ^ф ⁿ0^Т1 ⁸у4^т 3⁽ Y ^- в ф ⁺ ₃ 1----------------- ⁿ 0ЧУ4^Т 3⁽ Y - а ⁾⁽<	ⁿ 0 ^Т 1 4^Т 3⁽ У ^- ^а ⁾⁽ ⁸ ^- ^в ⁾/ ’ ( z z _fi + z ) в ₂ ° J ( Y - 8 ) и -------------------Hl u , n , к ) + ( у - а )( 8 - в ) F ( u , к ) - ф' У - в ) ⁸ ) ------------П( u ₀, n , к ) + а )( 8 - в ) ------- F ( u ₀, к ) У - в )
		в < £ < Y	^ в-а ) -Ру - в ^пП ф ( у-а ) - ( у - 3 )sin Ф	■ /⁽ ^р 0 ^- ^в ⁾⁽ ^y ^- ^а ) u₀ _ arcsin „ —0------------ ( р ² - а )( Y - в )	в ( Y - а ) - а ( y - в ) sn	2 n 0 ^Т 1 4^Т3 ( У ^- ^а ⁾⁽ ⁸ ^- ^в ⁾/ п " ( z z _fi + z ) _ в z 0
				. /⁽ Р ² ^- ^в ⁾⁽ Y ^- ^а ) u _ arcsin —z---------- \ ( р ² - а )( y - в ) z' _--- ₃ , ^в =F ( u о , k ) ⁿ o ^T i ³ 4^T 3⁽ Y ^- ^а ⁾⁽ ⁸ ^- ^в ) k 2 _ ( 8 - а )( y - в ) ( Y - а )( 8 - в ) n _ а ( в - Y ) ^П в ( у - а )	^р ⁽ Y ^- ^а ) ^- ⁽ Y ^- ^в ⁾ ^sn ² 1 в ф ф ^_ ф 0 ⁺ 3 „ г ⁿ 0 ^т 1 ^ав4^т 3 в ф ⁺₃ /---------------- ⁿ 0 ^Т 1°Р3⁽ у ^- ^а ⁾⁽< , ^вф ⁽ ^а ^- ф ⁼ ₃ /------- ⁿ 0 ^т 1 ав4^т 3 ⁽ У - в ф ⁺₃ /---------------- ⁿ 0 ^Т 1 °Р ⁽ ^У ^- ^а ⁾⁽<	ⁿ 0 ^Т4^Т 3⁽ У ^- ^а ⁾⁽ ⁸ ^- ^в ⁾/ ( z - z _n + z ) в z ⁰ J ( а - в ) _n П ( u , n , к ) + ( у - а )( 8 - в ) F ( u , к ) - ф' ? - в ) в ) ------------n( u ₀, n , к ) + а )( 8 - в ) ------- F ( u ₀, к ) ? - в )

-1

a < £ < p

^ a ( 3 - p ) +3Р-а ^ ^х П ф ( 3 - в ) + ( e — a )sii² ф

. ( p ² - a )( 3 - в )

u_n = arcsin —⁰—

V ( 3 - p^(в - a )

a ( 3 - в ) + 3 ( в - a ) sn

2 ⁿ 0 ^T 1 J ^T 3 ⁽ Y ^- ^a ⁾⁽ ³ ^- ^в ⁾ , _n

[ p ._ ⁽z - z ⁰ ⁺ ^z ⁾

. ( p ² - a )( 3 - в )

( 3 - в ) - ( в - a ) sn ²

в ф

Ф = Ф o ⁺ ;

n o T i ao ^ c з в ф

⁺ 3.

ⁿ 0 ^T\³P^T з ⁽ Y ^- ^a X °

, вф ( 3 -

^ф = . —

ⁿ 0 ^T i ^a3pT ⁽ ^Y ^-

в ф

⁺ 3. ,-------

ⁿ 0 ^T 1 ^{3 T} 3 ⁽ Y ^- ^a ⁾⁽ ³

n 0 ^T 3, V ³ ^ - ^a >( ° - ^в > ₍_ _ - в ₂ J

3 - a ) , .

П ( u , n , k ) +

( Y - a )( 3 - в )

F ( u , k ) - ф'

- в )

------------П( u ₀, n , k ) +

a )( 3 - в )

---^F ⁽ ^u 0 , ^k )

^- ^в )

u arcsin

\ ( 3 - p ²)( в - a )

z = ₃ ------ z-----------F ( u o , k )

n 0 T Цт 3⁽ Y ^- ^a ⁾⁽ ³ ^- ^в ⁾

k 2 = ( в - a )( 3 - y )

( Y - a )( 3 - в )

3 ( в - a )

n =

a ( 3 - в )

Y < ^ < 5

. Y ( 3 - в ) - в ( 3 - Y )siI⁰ Ф ( 3 - в ) - ( 3 - y )sit² ф

■ ( P ² - Y )( 3 - в )

u_n = arcsin —0-

V ( P o ² - в )( 3 - Y )

Y ( 3 - в ) - в ( ³ - Y ) sn

ⁿ 0 ^T i -My ^- ^a ⁾⁽ ³ ^- ^в ⁾. .

„ ⁽ z z 0 ⁺ z )

L ^в z

. ( p ² - y )( 3 - в )

u = arcsin —z----------

( p ² - в )( 3 - Y )

z = ₃ ,------ z------------F ( u o , k )

n 0 T -^ 3⁽ Y ^- ^a ⁾⁽ ³ ^- ^в ⁾

k 2 = ( в - a )( 3 - Y )

( Y - a )( 3 - в )

n =

Y ( 3 - в )

P -

( 3 - в ) - ( 3 - Y ) sn ²

в ф

^ф = ^ф 0 ⁺ 3 _R r-

ⁿ 0 ^Т 1 У^вР^Т 3

в ф

⁺ 3 /---------------

ⁿ 0 T 1 Л л/ Т 3 ( Y - a )(<

, в ф ( в -

^ф = 3 „

ⁿ 0 ^T 1 Y(iP^T 3 ⁽ Y ^-

в ф

⁺ 3 „ w

ⁿ 0 ^T i Л^т 3 ⁽ Y ^- ^a ^)(<

ⁿ 0 ^T 1 ³V ^T 3 ⁽ Y ^- ^a ⁾⁽ ³ ^- ^в ⁾, -----¹------------------( z - z _n + z )

в ₂ J

в - Y ) ,3

П ( u , n , k ) +

( Y - a )( 3 - в )

F ( u , k ) - ф'

3 - в )

Y ) / x

a )( 3 - в ) ⁿ⁽ ^u °" n ' k ^{) +}

3 - в ) ^F ⁽ ^u ^0, ^k )

Два вещест-венных и два комплек сных

3 < £ или

5 < Y

t 2 ф _— cos 9 1 ( 5-^ ) , g 2 cos 9 ₂( ^-Y ) ^,

3 + у 3 - у v - cos ф

% — ,

2 2 1 - v cos ф

⁹ 1 -

⁹ 2 -

острый , тупой ,

cos 0

3 - Y ----’ tg

cos 0

2 ¹

2 am

² ^c 0 ⁿ 0 ^Т 1 ³ 3^3 ,

, ( z z 0 + z )

^ P z ( - cos 0 ₁cos 0 2 ) 1 ₄

u 0 — 2 arctg

u — 2 arctg

z, _— P z ( ~ ^cos ⁹ 1

² c 0 n 0 ^T

2 ⁹1 - ⁹

k — sin —---

b — 3± ( 3 -

cos 9 1 ( 5-p 2 )

^cos 9 2⁽ p 0 -Y )’

^Р

_ cos 0 ₂ 2

¹ ⁺ л ^tg

cos 0 1

1 f

² ^c 0 n 0 ^T\ y„3 ₍ J

( z z ₀ + z )

P _z ( - cos 0 1 cos 0 ₂) ¹² ^J

cos 9 1 ( 5-p ²)

cos 9 ₂ ( p ² -y)’

cos 9 ₂ )¹²

₃ ² F ( u ₀, k ),

1 V^T 3

2 ^,

Y ) - ( 3 - У ) v
Y ) - ( 3 + Y ) v '

Р ф ⁽ - cos 0 1 cos 0 2⁾ ^V2 ⁽ 1 + b v )

Ф — ф 0 + з , I¹ 1⁽ u )

^c 0 ⁿ 0 ^Т 1 J ^Т 3 ^[ ⁽ ³ ^- Y ) ^- ^v ⁽ ³ ⁺ Y ) J

P„ ( - cos 0 1 cos 0 ₂ )¹² v ф _r ¹ ---------------3 F ( u , k )

^c 0 ⁿ 0 T 1 ЦТ 3 ^[ ⁽ 3 - Y ) - v ⁽ 3 + Y ⁾ ^J

, Р ф ⁽ ^- cos ⁰ 1 co ^s ⁰ 2⁾ ^V 2⁽ 1 ⁺ ^b ^v )

ф — + __ 1 1 ( u 0 )

C 0 n 0 Т 1 4^T 3 [ ⁽ ³ ^- Y ) ^- ^v ⁽ ³ ⁺ Y ) J

P„ ( - cos 0 , cos 0 ) ¹² v

^ф 3 , ¹ ------------------3 F ( u 0, k )
^c 0 ⁿ 0 ^Т 1 4^Т 3 К ³ ^- Y ) ^- ^v ⁽ ³ ⁺ Y ⁾ ^J

-1

У < ^ < 3

0 1 , 0 2 - острые .

Вид решения такой же, как в случае 3 < ^ или _е , ( - cos 0 cos 0 2 ) 1²

^ < y , с учетом замены множителя ----- 1----24—

c ₀

на множитель - ( ^cos ⁰ 1^cos ⁰ 2^)/ .

c ₀

Четыре комплек сных,

b 1 > b 2

- ^ < £ <

f 0 + 0 )

^ — b 1 + c 1 tg ф + 2 1

0 3 , 0 4

u ₀ — arctg

u — arctg

0 5 /2 - fp 0 - b '

острые.

9 3 +9 ₄

Р — b 1 + C 1 tg

[ 2 n „3, R ^f 4 c 2 I¹’ ₊ 1

0 3 + 0 4

⁺ 2

( z zn 1 z )

P z l cos 0 ₅ J ⁰

l c 1 4 fp ² - b 1

2 ’

9 3 +9 4

2 ’

в ф f cos 9 з ] f^J9 3 +9 4 i

-1 ‘Ч u ) -

, в (cos 0 ) ¹²

z ^— 3 1/2 F ⁽ ^u 0^, ^k )

² n 0 ^Т 1 4 3 3 ⁽ ^c 1 ^c 2 )

k ² — sin ² 0 5

, 0₃ + 0 4

^b 1 ⁺ ^c 1 tg 2

c ^— , 0 3 + 0 4 .

^c 1 ^b 1 tg ₂

2 n ₀ ф ^—Ф 0 +

^вф

т 3 тг ; i c 1 c 2 4 ci 2 л

9 +9

^c 1 ^b 1 tg ₂

f cos 9 5 Y2 f 9 3 +9 ₄ i

² ⁿ 0 ^T1V^T 3

c ₁

cc ^g 2

^l 1’ F ( u , k ) ф' -

- b . tg ⁹- 3^

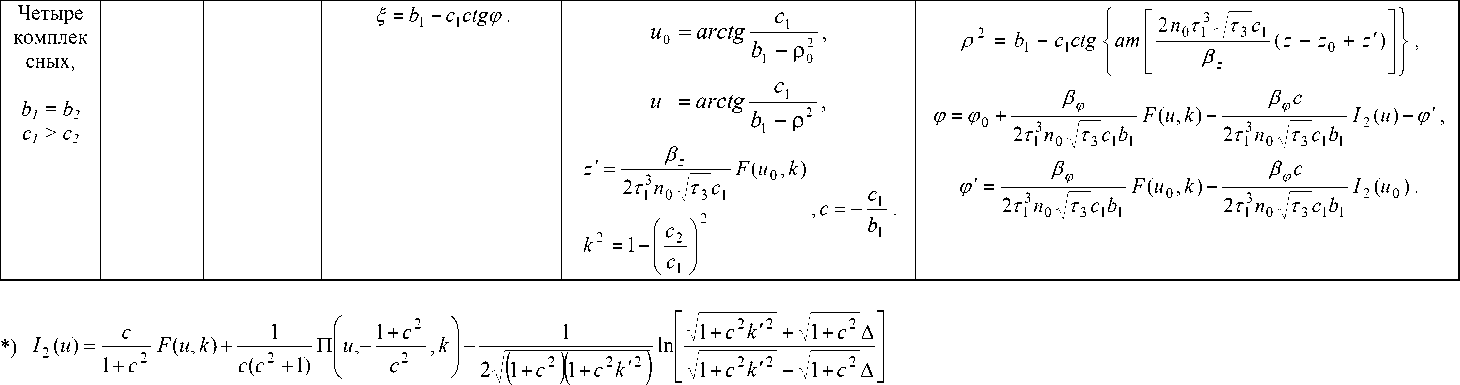
k ' , \ - определены в (36).

Статья научная