Транспортные автомобильные потоки - введение в вероятностный подход

Транспортные автомобильные потоки - введение в вероятностный подход

Автор: Замятин А.А., Малышев В.А.

Журнал: Труды Московского физико-технического института @trudy-mipt

Статья в выпуске: 4 (8) т.2, 2010 года.

Бесплатный доступ

Вероятностные модели транспортных потоков, отражающие качественные явления на ав- томагистрали, весьма разнообразны: от массового обслуживания середины прошлого века до статистической физики и процессов с локальным взаимодействием. В статье перечисле- ны возможные постановки задач и подробно разобраны некоторые примеры.

Короткий адрес: https://sciup.org/142185704

IDR: 142185704

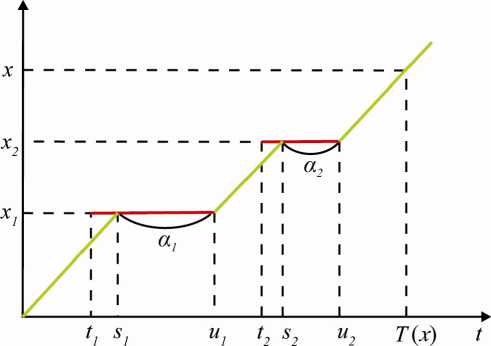
Список литературы Транспортные автомобильные потоки - введение в вероятностный подход

  • Blank M. Ergodic properties of a simple deterministic traffic flow model//J. Stat. Phys -2003. -V. 111. -P. 903-930.
  • Blythe R.A., Evans M.R. Nonequilibrium steady states of matrix-product//Journal of Physics A: Mathematical and Theoretical. -2007. -V. 40, N. 46.
  • Botvich D.D., Zamyatin A.A. On fluid approximations for conservative networks. Markov Processes and Related Fields. -1995. -V. 1, N. 1. -P. 113-141.
  • Buslaev A.P., Prikhodko V.M., Tatashev A.G., Yashina M.V. The deterministic -stochastic flow model. -e-print arXiv: physics/0504139 v1, 2005.
  • Caceres F., Ferrari P., Pechersky E. A slow-tostart traffic model related to a M/M/1 queue//Journal of Statistical Mechanics: Theory and Experiment. -2007. -V. 2007.
  • Cox D.R., Isham V. Point processes. -Chapman and Hall, 1980.
  • Daley D., Vere-Jones D. An Introduction to the Theory of Point Processes. -Springer, 2003. -V. 1.
  • Derrida B. Non-equilibrium steady states: fluctuations and large deviations//Journal of Statistical Mechanics: Theory and Experiment. -2007.
  • Fayolle G., Malyshev V., Menshikov M. Topics in the constructive theory of countable Markov chains. -Cambridge University Press, 2008. -2nd edition
  • Fayolle G., Lasgouttes J.-M. Asymptotics and Scalings for Large Product-Form Networks via the Central Limit Theorem. -Markov Processes and Related Fields, 1996. -V. 2, N. 2. -P. 317-349.
  • Helbing D. Verkehrsdynamik. -Berlin: Springer, 1997.
  • Helbing D. Traffic and related self-driven many particle systems//Rev. Mod. Phys. 73. -2001. -P. 1067-1141.
  • Jost D., Nagel K. Probabilistic Traffic flow breakdown in stochastic car following models//Traffic and Granular Flow -2005. -Part 2. -P. 87-103.
  • Kelly F. Reversibility and stochastic networks. -N.-Y.: Wiley, 1979.
  • Kerner B.S. Introduction to modern traffic flow theory and control. -Springer, 2009.
  • Lighthill M.J., Whitham G.B. On kinematic waves: II. Theory of traffic flow on long crowded roads//Proc. R. Soc. -London, 1955. -V. 229. -P. 281-345.
  • Lotito P., Mancinelli E., Quadrat J.-P. A min-plus derivation of the fundamental car-traffic law//Automatic Control IEEE Transactions. -2005. -V. 50. -P. 699-705.
  • Malyshev V., Yakovlev A. Condensation in large closed Jackson networks//Ann. Appl. Probab. -1996. -V. 6, N. 1. -P. 92-115.
  • Prigogine I., Herman R. Kinetic theory of vehicular traffic. -N.-Y.: Elsevier, 1971.
  • Renyi A. On two mathematical models of the traffic on a divided highway//Journal of Applied Probability. -1964. -V. 1. -P. 311-320.
  • Gartner N.H., Messer C.J., Rathi A.K. Revised Traffic Flow Theory. A state-of-art report. -Washington DC: Transportation Research Board, 2001.
  • Serfozo R. Introduction to stochastic networks. -Springer, 1999.
  • Solomon H. Geometric Probability. -SIAM, Philadelphia, 1978.
  • Solomon H., Wang P. Nonhomogeneous Poisson fields of random lines with applications to traffic flow//Proc. Sixth Berkeley Symp. On Math. Statist. and Prob. -Univ. of Calif. Press, 1972. -V. 3. -P. 383-400.
  • Gartner N.H., Messer C.J., Rathi A.K. Traffic flow theory: A state-of-the-art report. -Washington DC: Transportation Research Board, 2001.
  • Афанасьева Л.Г. Очерк исследования операций. -М.: Изд-во МГУ, 2007.
  • Буслаев А.П. Вероятностные и имитационные подходы к оптимизации автодорожного движения. -М.: Мир, 2003.
  • Замятин А.А., Малышев В.А. Накопление на границе для одномерной стохастической системы частиц//Проблемы передачи информации. -2007. -T. 43, вып. 4. -С. 68-82.
  • Иносэ Х., Хамада Т. Управление дорожным движением. -М.: Транспорт, 1983.
  • Кингман Д. Пуассоновские процессы. -М.: МЦНМО, 2007.
  • Кокс Д., Смит В. Теория восстановления. -М., 1967.
  • Малышев В.А., Минлос Р.А. Гиббсовские случайные поля. -М.: Наука, 1985.
  • Малышев В.А. Случайные грамматики. -Успехи Мат. Наук, 1998. -Т. 53, вып. 2. -С. 107-134.
  • Рюэль Д. Статистическая механика. Строгие результаты. -М.: Мир, 1971.
  • Федорюк М.В. Метод перевала. -М.: Наука, 1977.
  • Хейт Ф. Математическая теория транспортных потоков. -М., 1966.
  • Четверушкин Б.Н., Трапезникова М.А., Фурманов И.Р., Чубарова Н.Г. Макро-и микро-скопические модели для описания движения автотранспорта на многополосных магистралях//Труды МФТИ (специальный выпуск, посвященный математическому моделированию транспортных потоков, под ред. акад. В.В. Козлова). -2010. -Т. 2, № 4(8).
Еще
Статья научная
QR-код для установки приложения SciUp Наведите камеру и скачайте бесплатное приложение SciUp