Трехфазная гидродинамическая модель фазового поля со стабилизацией уравнения Кана-Хилларда

химического потенциала:

∂C ∂t

-div j = -div(-M V e ) = M V ² ^.

Здесь C — концентрация; j — поток диффузии; M — коэффициент мобильности; µ — химический потенциал определяется через функцию свободной энергии E :

E = -C E = J f (C,VC) dV, Ω где f — плотность функции свободной энергии. При этом делается важное допущение, что, в отличие от классической термодинамики [6], свободная энергия зависит не только от состава вещества (концентрации), но также и от градиентов концентрации. Безградиентная часть представляется в виде двухъямного потенциала, минимумы которого соответствуют равновесию двух разных фаз; градиентное же слагаемое отвечает за межфазные эффекты. Чистые фазы вещества задаются величиной концентрации C = 0 и 1 (либо другими ее значениями, в зависимости от нормировки модели), а граница раздела определяется резким (тонким, но имеющим конечную толщину) переходным слоем. Другое встречающееся в литературе название моделей фазового поля — модели с диффузной границей раздела, что подразумевает некоторое противопоставление моделям сквозного счета, которые преимущественно используются для моделирования строго несмешивающихся сред с границей раздела, стремящейся к нулю (sharp interface models). Напротив, фазово-полевые модели обладают гибкостью и позволяют моделировать динамику как несмешивающихся, так и смешивающихся систем (в том числе частично смешивающихся). Это достигается путем выбора функции свободной энергии и значений ее параметров.

Классические модели фазового поля учитывают только процесс диффузии, что, в частности, дает возможность теоретически описывать такие процессы при фазовом расслоении, как спинодальный распад (spinodal decomposition [7] ) и зародышеобразование (nucleation [8] ). Встраивание в гидродинамические модели (в систему уравнений Навье–Стокса) происходит за счет добавления в уравнение движения напряжения Кортевега [9] , определяемого через дивергенцию векторного произведения градиентов концентрации. В рамках гидродинамических фазово-полевых моделей возможен, например, учет неустойчивости Рэлея–Тейлора [10] , динамики вытеснения в капилляре [11] и другого. Теория фазового поля также позволяет принимать во внимание различную смачиваемость твердой поверхности [12] и другие эффекты [13] .

К недостаткам метода фазового поля можно отнести сложности в численной реализации [14] . Несмотря на ослабленные требования малости толщины переходного слоя по сравнению с другими моделями, для корректного моделирования физических процессов в большинстве случаев необходимо задавать границу раздела с конечным, но малым по толщине переходным слоем, что накладывает существенные ограничения на размер вычислительной сетки. Для устойчивости численного счета, с одной стороны, необходимо, чтобы сетка по толщине переходного слоя содержала приблизительно 4–5 узлов, однако для обеспечения достоверности получаемых результатов число узлов обычно оказывается в несколько раз больше. С другой стороны, уравнение диффузии Кана–Хилларда является уравнением в частных производных четвертого порядка, в котором присутствует бигармонический оператор. Реализация явной по времени схемы приводит к ограничению величины шага по времени: τ ∼ h ⁴ . Вследствие этого реализация явных схем становится не эффективной, но тем не менее, в силу своей простоты, подходы на основе этих схем весьма популярны. Неявные схемы дискретизации уравнения Кана–Хилларда порождают системы уравнений с плохо обусловленными матрицами, и фактически шаг по времени приходится выбирать сопоставимым с применяемым при явной схеме. Другим подводным камнем при численной реализации метода фазового поля является необходимость соблюдения энергетической устойчивости алгоритма [15] , то есть неувеличения со временем функции свободной энергии:

dE

• -Г < 0. dt

• 2.    Модель трехфазной среды

Однако за последнее десятилетие наблюдается значительный прогресс в усовершенствовании неявных численных методов расчета с использованием уравнения Кана–Хилларда, среди которых можно выделить метод расщепления [15] (splitting technique), улучшающий энергетическую устойчивость алгоритма путем представления свободной энергии в виде двух частей: одна вычисляется явно (на предыдущем временном шаге), другая — неявно (на новом шаге). Схемы с добавлением фиктивного стабилизирующего слагаемого [14] позволяют уменьшить спектральный радиус матрицы СЛАУ для итерационных алгоритмов.

Все вышеописанные подходы применяются преимущественно в случаях двухфазных систем. Безусловно, модели существенно усложняются при обобщении на многофазные структуры. Теория фазового поля в силу своей гибкости и универсальности — один из наиболее перспективных подходов для симуляции многофазных явлений. Несмотря на имеющийся прогресс в разработке подобного рода моделей [16] , по-прежнему остается множество сложностей и нюансов при их численной реализации. В текущей работе излагается собственная оригинальная реализация комбинированной модели Навье–Стокса и многофазного метода фазового поля, в которой система уравнений Кана–Хилларда модифицируется с помощью добавления фиктивной производной химического потенциала, что позволяет увеличить временной шаг интегрирования и повысить эффективность численного интегрирования.

В основу разрабатываемой многофазной модели фазового поля положены идеи, опубликованные в работах [17, 18] . Основные положения модели состоят в следующем. Полную функцию свободной энергии записываем как

E =

[ 12F(c i ,c 2 ,с з ) + 3 "X i V_n ² + 3 -Л' , VC , ² + 3 "Л з Vc- ² 8             8             8

Ω

dV.

В уравнении (1) F (c 1 ,c ₂ ,c ₃ ) представляет собой трехъямный потенциал (аналог классического двухъямного потенциала для двухфазной среды); ε — параметр, отвечающий за толщину межфазной границы; Σ i — так называемые коэффициенты распространения (spreading coefficients). Числовые коэффициенты (12 и 3/8) подобраны удобными для использования модели. Система уравнений Кана–Хилларда принимает следующий вид:

^dC i = М_г V ² *,

∂t ^{i i ,}

δE      ∂F

* = SC+в=12 dC- здесь β — множитель Лагранжа

3          „ _      _     .

- eZ - V^C - + в  (i = 1,2,3);

X 4 Z t dF ^в         Zi dC - ,

где ZT = 3(1 /Z1 + 1/Z2 + 1/Z3)-1. Он необходим для удовлетворения условия, налагаемого на концентрацию трехфазной системы: C1 + C2 + C3 = 1. Кроме этого, вводим дополнительные ограничения на коэффициенты мобильности: M0 = M1Z1 = M2Z2 = M3Z3, и на сумму химических потенциалов: *1/Z1 + *2/Z2+*3/Z3 = 0. Тогда одно из уравнений для концентрации становится зависимым. После его исключения получаем следующую систему уравнений Кана–Хилларда:

∂C i   M 0 2

dt   Z i ^v *

* =^4Z t X Z j (dC-^-4 C i    ⁽ⁱ=1,²⁾.                    ⁽³⁾

Коэффициенты Σ _i при этом оказываются связанными с попарными коэффициентами поверхностного натяжения:

Z i +Z 2 ---0---= ^J 12 ,

^Z 1 + ^Z 3 2

= ^J 13 ,

^Z 2 ^{+ Z} 3 2

= °23.

Дополняем систему уравнений Кана–Хилларда (2) , (3) моделью Навье–Стокса [19, 20] для несжимаемой жидкости. В результате имеем:

— + (vV)v = —Vp+ ^-V2v + ^X^iCi — 77^ECiV*-dt            Re    Fr ^    We div v = 0, dCi + (vV)C- = m V

∂t            Σ i

Re =

ρ ^∗ UL η ^∗

••          , gl

We= '    ' ,

σ ∗ ,

Ф- —

ρ i - ρ ^∗ ρ ^∗

Re — число Рейнольдса (вязкость фаз одинаковая); Fr — число Фруда; We — число Вебера; ф_- — контраст плотности. Для удобства формально оставляем уравнение Кана–Хилларда в первоначальном виде, для чего переопределяем параметры в новых единицах измерения: коэффициент мобильности L/U · M 0 → M 0 , параметр ε · L → ε , коэффициенты Σ σ ^∗ → Σ i . Заметим, что химический потенциал (с размерностью энергии) в теории фазового поля, строго говоря, является не совсем таковым; здесь это удельный химический потенциал — энергия в единице объема. Обезразмериваем его так: µ · σ ^∗ /L → µ .

На твердых стенках систему уравнений (4) – (7) дополняем граничными условиями:

v = 0,

" = 0, ∂n

dC =0. ∂n

Здесь n — координата, нормальная к твердой стенке. Условие для скорости — стандартное условие прилипания на твердой стенке. Условие для химического потенциала является следствием выражения j n = 0 (считаем, что нормальная компонента потока вещества равна нулю). Условие для концентрации на твердой границе задает смачиваемость последней, в данном случае дС/дп = 0 соответствует нейтральному углу смачивания, который равен п/2.

Уравнение Навье–Стокса решаем с помощью проекционного метода. На первом шаге алгоритма вычисляем промежуточное значение скорости без учета градиента давления — квазискорость u ^∗ :

u * = v +^т (^-(W) v +^ V ² v +| X ^ i C i ^- 1— X C iWi ) , Re Fr-^ We-^

ii где значения в правой части берем с временного шага (п — 1). На втором этапе алгоритма решаем уравнение Пуассона для давления:

2     div u *

p τ.

На третьем, последнем, шаге алгоритма по рассчитанным значениям квазискорости и давления находим поле истинной скорости:

v = u * — т V p.

Как написано во Введении, при численном решении уравнения Кана–Хилларда возникает ряд технических сложностей, одной из которых является значительная величина спектрального радиуса (то есть максимальное собственное число матрицы A max ) при большом шаге по времени (т ). Для устойчивости традиционных итерационных алгоритмов, таких как методы Якоби и Гаусса–Зейделя, необходимо выполнение неравенства A max < 1, что фактически достигается лишь при весьма малых, сопоставимых с явной схемой значениях т .

В текущей работе предлагается представленный в статье [14] метод обобщить на многофазные системы. Опишем кратко основные идеи данного подхода в одномерном случае.

При дискретизации на основе неявной схемы Эйлера 1-го порядка по времени (Backward Euler method) получаем матрицу СЛАУ следующего вида:

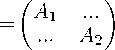
A i =

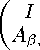
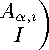
(i = 1,2).

В выражении (8) матрица всей системы уравнений Кана–Хилларда A состоит из блоков A ₁ и A ₂ , каждый из которых в свою очередь включает блоки I,A α,i ,A β,i ; I — единичная матрица; A α,i ,A β,i — трехдиагональные (в двухмерном случае пятидиагональные) матрицы:

A a,i =

/ 2a i

- α i

- α i ···

^2a i   ^{— a} i

0 \

···

/—2ei ei ei    —2ei

Ae,i =      .        ..

⁰ A

···

\ 0      •••     - a i    2a i/

\ 0     ••• e i   -WJ

Значения α i и β i определяются через параметры дискретизации и коэффициенты модели:

_ Mo т       3 eS ai Si h2,     ei 4 h2 ’ где h — пространственный шаг сетки, τ — временной шаг интегрирования. При этом фактически реализуется полунеявная схема, в которой на новом временном шаге (n) дискретизируются только линейные слагаемые с оператором Лапласа, нелинейные слагаемые рассчитываются явно на временном шаге (п — 1) и записываются в правой части СЛАУ В работе [14] показано, что спектральный радиус равен Amax = 4у^ов и Amax = 16ав, соответственно, для методов Якоби и Гаусса-Зейделя. Границы устойчивости методов совпадают: ов < 1/16. В двумерном случае граница устойчивости определяется условием: aft < 1/64.

В случае блочной матрицы A данный критерий применим для каждой подматрицы A i , устойчивость же системы в целом будет определяться максимальным собственным числом подматриц A i . Однако, как легко видеть, произведение α i β i не зависит от коэффициентов Σ i , следовательно, на устойчивость численного метода выбор Σ i также не влияет. Фактически остается лишь один механизм регулирования спектрального радиуса — уменьшение шага по времени τ .

Модифицируем химический потенциал путем добавления в его исходное выражение фиктивной релаксационной производной по времени:

-^-К =^4S T X F ( IF — IF- V ^{3 £S} i ^V 2 C i    (i =^1,2).

dt              “S j —^>i —^y j     4

i̸ = j

После дискретизации временной производной kT^ = kT^ ^n 1 = k(^n—Mn-1) ∂t          τ перепишем выражение для химического потенциала:

/    3 eS i y² C i V_ / 4 S _T X 1 / dF dF A k V^{- 1}

Mi + 471+k)   = (1+k)V ^AdCi - dCj J + (1 + k) Mi i̸=j

Таким образом, с помощью данной процедуры можно в k раз уменьшать значение параметра β , что дает возможность в k раз увеличивать временной шаг τ и соблюдать ограничение для спектрального радиуса A max < 1. Предпринятые действия, безусловно, вносят дополнительную ошибку в численное решение уравнения Кана–Хилларда, в особенности, при больших значениях k , так как нарушается принцип неувеличения полной свободной энергии: dE/dt < 0. Однако при сохранении релаксационного параметра таким, что kT ^ 0, результаты расчетов полностью соответствуют немодифицированной модели Кана–Хилларда; как показано в работе [14] (для двухфазной среды), в зависимости от конфигурации задачи возможно выбирать параметр из диапазона k ^ 20... 100 без существенного снижения точности моделирования.

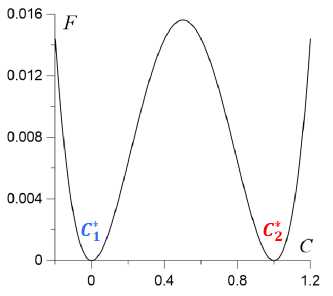
Отдельного рассмотрения требует также выбор безградиентной части функции свободной энергии: F(C 1 ,C 2 ,C 3 ), где C 3 = 1 - C 1 - C 2 . Даже для двухфазной среды в ряде задач возникает необходимость замены стандартной функции C 2 (1 — C ) ² (см. Рис. 1 a ). При реализации метода фазового поля возможно появление артефактов, например, превышения (overshooting) значений поля концентраций, имеющих физических смысл. Для преодоления этой проблемы можно, в частности, использовать кусочную функцию и в интервале C <  0 и С> 1 применять функции с более крутым наклоном, что, однако, может привести к новым артефактам численного счета. Следовательно, выбор функции свободной энергии является одной из важнейших задач данной модели. Это особенно актуально для многофазных систем, поскольку число потенциальных артефактов в этом случае

( а )

( в )

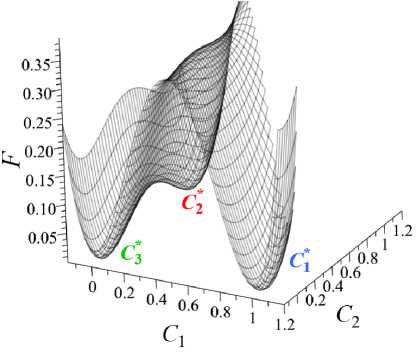
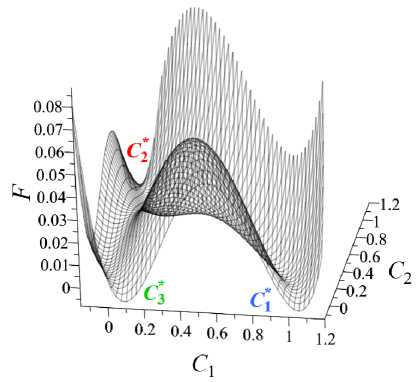
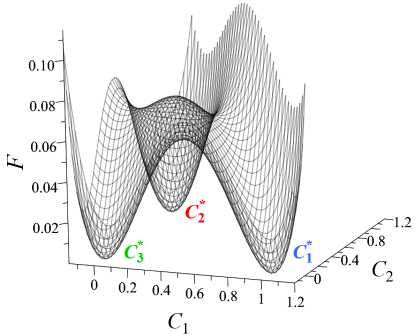
Рис. 1. Представление функции свободной энергии F (9) : безградиентная часть – двухфазный двухъямный потенциал ( а ); при S i = ^ 2 = S 3 = 1 ( б ); при S i = 10 ,£ 2 = S 3 = 1 ( в ); при S i = 1 ,^ 2 = — 0 . 7 ,Х з = 1 ( г ); значения С, C 2 , C 3 вблизи минимумов функции F соответствуют концентрациям чистых фаз

( г )

значительно увеличивается. Как минимум, ожидаем, что в случае полного отсутствия одной из фаз трехфазная модель будет воспроизводить динамику двухфазной системы.

Анализ литературы и тестовые расчеты показали, что функция вида

F (C 1 ,C 2 ,С з ) = ^(^ 12 C ? C ₂ ² ■ - 13 C 2 C 3 + « 23^3 + С 1 С 2 С з ( ^ 1 С 1 + ^ 2 С 2 + £ з С з )) =

= Д- (I ¹ C 2 (1 - C i ) ² +1 ² C ₂ ² (1-C 2 ) ² +1 ³ С з ² (1 — С з ) ² ),                      (9)

предложенаная в работе [17] , удовлетворяет заданным критериям. В выражении (9) ∆ — масштабный фактор, который в работе полагаем следующим: Д =1. Функция (9) представлена на рисунке 1 для трех характерных случаев: на фрагменте 1б — это симметричный трехъямный потенциал, в котором все коэффициенты Σ i равны, то есть поверхностное натяжение на межфазных границах одинаково. На фрагменте 1в можно видеть большой потенциальный барьер между 1-й и другими фазами, тогда как между фазами с концентрациями C ₂ и C 3 барьер значительно ниже, что соответствует ситуации Σ 1 >> Σ 2 ,Σ 3 . Таким образом, моделируется случай больших поверхностных натяжений σ 12 и σ 13 и малого поверхностного натяжения σ 23 . В случае на рисунке 1г £ 1 = 1, £ 2 = -0.7, £ ₃ = 1, то есть имеет место потенциальный барьер между фазами C 1 и C ₃ , что отвечает большому поверхностному натяжению между этими фазами и сравнительно малым натяжениям σ 23 , σ 12 .

• 3.    Численная реализация

Численный алгоритм определения динамики многофазных сред реализуем на языке программирования C++ совместно с процедурой визуализации полей концентрации при помощи библиотеки компьютерной графики OpenGL 4.6. Рассматриваем квадратную область (x,y G [0,1]). Для дискретизации прибегаем к методу конечных разностей при условии построения однородной сетки: x i = i • h x , y j = j • h _y , i = 0...N x , j = 0...N _y , где i,j — пространственные индексы сетки, N = N _x = N _y — число узлов, h = h x = h _y = 1 /N _x = 1 /N _y — шаг сетки. Полагаем, что время t = n • т , где n — временной индекс, т — шаг по времени. Тогда дискретный аналог произвольной функции ф(x,y,t) на шаге по времени n станет следующим: ф П j . Сделаем оговорку: поскольку в данном разделе используются общепринятые обозначения пространственных индексов i,j , то далее, во избежание путаницы, номер компонента фазы будем обозначать верхним индексом в круглых скобках: C _i ⁽¹ _j ^{) ,n} , C _i ⁽² _j ^{) ,n} , C _i ⁽³ _j ^{) ,n} .

Производные по времени аппроксимируем так:

∂φinj φinj-φin,-j 1 dtт

Дискретные аналоги пространственных производных принимают вид: – производных 1-го и 2-го порядков во внутренних узлах

∂φ iⁿj φ iⁿ +1 ,j - φ iⁿ - 1 ,j     ∂φ iⁿj φ iⁿj +1 - φ iⁿj - 1

dx          2h      , dy          2h,

^nj = ФП+1,3-Vn-lj-2Фп   ^Ф^ = фП;+1 -фП;-1 - 2-"j dx2               h2           ’ dy2               h2’

– первых производных на границе области

■   = -3ф n,j +Mj- - Ф П, ₃   ^d    JNj-dN - j ^ N^

dx             2h         , dx                  2h’ дфП,0 _ —3фП0 +4фП1 — фП2   дфг^у _~3фг^у +4фn^y-1 —фn^y-2.

dy =        2h        ’ dy =             2h’

– вторых производных на границе области

• d²^ Mj —^ nj+-^j д2Ф^2Ф^л-5ф^-ы+^ф^^

dx2                h2            ,     dx2

dyn o = 2ф П о - 5ф П 1 +4ф П 2 - ф П з

∂y ²                h ²

^d 2y = ^2фn^y ^5фn^y-1 ^{+ 4ф}'\уу 2 ^фn^y-з

∂y2

Конвективные производные аппроксимируем центральными разностями:

(v nj -V) . = xj

∂φ _i ⁿ _j

,n dx + yij

∂φ _i ⁿ _j ∂y ^.

Системы уравнений Навье–Стокса и Кана–Хилларда решаем независимо друг от друга. К уравнениям Навье–Стокса (4) , (5) применяем проекционный метод. На первом шаге алгоритма вычисляем поле квазискорости (поле скорости без учета давления):

= v^ + t (- j V vh +R ^v 2 v^ ■ ■.'.   C+-Я C j ■ C

¹ ((i^),n^ⁿv-7 ^1),nx Л'*⁽²⁾’ ^п V7 ,/2)’ⁿi /^(3),ⁿ , ,⁽³⁾’ⁿA I we⁽C ij ^vM i,j + C^ vU ij + C i’j v^ i’j ) .

Поле давления получаем из решения уравнения Пуассона

V²pⁿ j = Tdiv u ⁿj

с помощью итерационного метода Гаусса–Зейделя. На заключительном шаге алгоритма находим истинное значение скорости на новом шаге vn+ 1 = unj -T Vpnj с учетом граничного условия прилипания: v = 0. Условие для давления на твердой границе получаем путем проецирования уравнения Навье–Стокса на нормаль к границе:

∂p _i ⁿ _j ∂ n

X ^d2 v nj

Re d n ²

♦ ^W" +Ф⁽^С^^п +^ ⁽³⁾ C i ⁽ j ⁾ ’ⁿ ). Н р              'J                   'J                   'J

Систему уравнений Кана–Хилларда аппроксимируем на основе полунеявной эйлеровой схемы, в соответствии с которой конвективные и нелинейные слагаемые записываются на предыдущем временном шаге:

С ⁽¹⁾ ’ⁿ4- rv(1)f »⁽¹⁾ ’ⁿ+ 9,,⁽¹⁾ ’ⁿ »⁽¹⁾ , ⁿ’l- Г ¹ ’ ⁿ' ¹ ^(nn. v^ r⁽¹⁾ ’^{n- 1}

C i’j ^{+a (-}M i +1 j ^{+ 2}M ij -P i-^ ) = C i’j    ^{- T} v j ^^v )Cjj

⁽¹⁾ ’ⁿ i ^в1 (s'¹-¹)’"   9<’⁽¹⁾ ’ⁿ i n⁽¹ ) - ⁿ\       ¹        ,,⁽¹⁾ ’^{n- 1} i f⁽¹ ) ^{,n- 1} \

^ ij  ⁺ k + 1⁽C i +1 ,j ²C i’j   ⁺C i -1 ’j )    k +1 k^ iij     ^+f i’j     J,

p⁽²⁾ ’ⁿ ।    ⁽²)z z/⁽²⁾ ’ⁿ-I- 9//⁽²⁾ ’ⁿ »^(2),n’l p⁽²⁾ ’^{n- 1} _T( _v ⁿ ,п\ х.(²л " 1

^C ij ^{+ a   ( -} ^ i +1 ,j ^{+ 2}^ ij     ^ i \ j ) = C i’j     ^-Tk^VM • ^v )C i,j

(2) ,n    ^{в (2)} _fp(2) ,n    _9r(2) ,n _r(2) ,nx ¹    (, (2) ,n- 1   ,(2) ,n- 1 \

^ ij  ⁺ k + 1⁽C i +1 ,j 2 C i,j ⁺C i -1 ,j )= k +1 \^ i ^l j’j      ^{+ f}ij     J’

и решаем при граничных условиях:

dC j dC j d^ ^ j, ¹ dp j ∂ n ∂ n ∂ n ∂ n

Концентрацию третьей фазы находим из условий:

(3) ’n          (1) ’n     (2) ’n (3) ’n        (3)   (1) ’n    (1)    (2) ’n    (2)

C i’j   =1   C i’j      C i’j ’  ^ i,j  = ^    ⁽^ i,j   /^   ⁺ r i,j   /^   )^.

Нелинейные функции f i ^l j'^{n 1} и J' ij)' "' ¹ определяем следующим образом:

(1) ,n - 1 f i,j

= 12

(£^(1> (Cj’ ^{n 1} (1

C ⁽¹⁾ ’^{n- 1} )(1 - 2C ⁽¹ ) ^,"^{— 1} ))-ДрС ⁽¹⁾ ’^{n- 1} C ⁽²⁾ ’ⁿ

1 c (3) ’П — 1

f j ¹ = 12 (s ^(2> ( C^ ^{n 1} (1- C^ ’" ¹

)(1 - 2C j ^{n -1} y) - S d С^’"^-1^’"

1 C (3) ’П — 1

.

Здесь

_v            6S ⁽¹⁾ S ⁽²⁾ S ⁽³⁾

^{S d} = SwS ^H S ¹ ) ^ ³ ^^ ²^^ .

Коэффициенты a ⁽¹⁾ , a ⁽²⁾ , в ⁽¹⁾ , в ⁽²⁾ , входящие в уравнения (10) , вычисляем по формулам:

„ (1)₌ M'       »(1) ₌ 3 ^S        _a(2>₌ MT      (2   3 er ⁽²

“      s rnh? ’     ^в 4 h ’    “     Г (2) h 2 ’    ^e 4 h ² •

Систему уравнений Кана–Хилларда, приведенных к дискретному виду, разрешаем с помощью итерационного метода Гаусса–Зейделя.

• 4.    Тестирование алгоритма расчета

  Во всех расчетах считаем, что числа Рейнольдса, Вебера и Фруда равны единице: Re = 1, We = 1, Fr = 1, а параметр, отвечающий за толщину межфазной границы, составляет: ε = 0.00025. Расчеты проводим на равномерной сетке h= 1/128. Полагаем, что параметр стабилизации уравнений Кана–Хилларда k= 100.

В качестве первого теста задаем конфигурацию, в которой C 2 = 1, y < 0.5 и C 3 = 1, y > 0.5, ав центре области находится круглая капля (C 1 = 1) радиусом R= 0.15. Рассматривам задачу в отсутствие гравитации: 1/Fr = 0. На рисунке 2 представлены случаи для различных характерных значений коэффициентов Σ i . На фрагменте 2а показан случай для Σ ₁ = Σ ₂ = Σ 3 = 1. В такой системе контактные углы на стыке трех фаз стремятся к значениям α 12 = α 13 = α 23 = 2π/3 (α ij обозначает угол напротив пары фаз i и j). Отклонение от ожидаемых значений, возможно, вызвано действием сторонних сил и начальным распределением фаз в системе. На фрагменте 2б приведен случай Σ 1 ≫Σ 2 =Σ 3 ; при такой конфигурации α 23 →π, α 12 =α 13 →π/2.

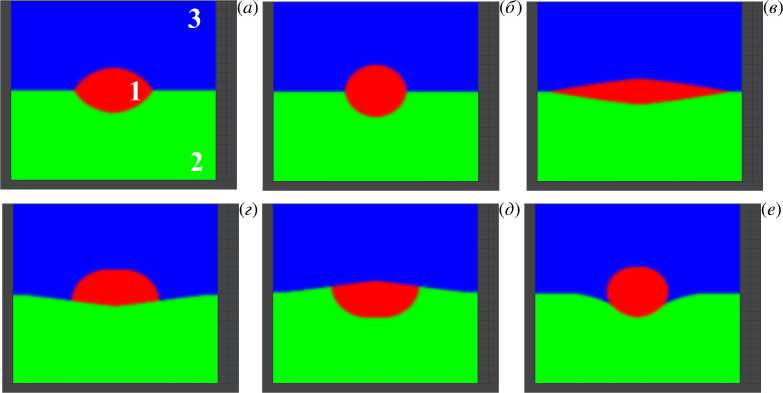
Рис. 2. Модель трехфазной среды при различных значениях коэффициентов Σ i : Σ 1 = Σ 2 = Σ 3 = 1 ( а ), Σ 1 = 100 , Σ 2 = Σ 3 = 1 ( б ), Σ 1 = 0 . 01 , Σ 2 = Σ 3 = 1 ( в ), Σ 1 = 1 , Σ 2 = 100 , Σ 3 = 1 ( г ), Σ 1 = 1 , Σ 2 = 1 , Σ 3 = 100 ( д ), Σ 1 = 100 , Σ 2 = 20 , Σ 3 = 1 ( е ); цифры на фрагменте ( а ) обозначают порядковые номера фаз; во всех случаях показана установившаяся равновесная система в момент времени t =0 . 5

Похожая ситуация реализуется для значений Σ 1 = 100, Σ 2 = 20, Σ 3 = 1 (см. фрагмент 2е ). Также наблюдается круглая капля фазы 1 ; форма капли обусловлена ее большим поверхностным натяжением, однако имеется нарушение симметрии между фазами 2 и 3 из-за разницы Σ ₂ и Σ 3 . Фрагмент 2в демонстрирует случай малого Σ ₁ ; видно, что капля стремится растечься на границе раздела фаз 2 и 3 . Отметим, что в литературе на русском языке для коэффициентов Σ i можно встретить название «коэффициенты растекания» (что отражено в результатах на фрагментах ( а ), ( б ) и ( в )), однако, вероятнее всего, в более сложных системах такая интерпретация не всегда очевидна.

Фрагменты 2г и 2д содержат два симметричных случая: Σ 2 ≫ Σ 1 = Σ 3 и Σ 3 ≫ Σ 1 = Σ 2 . Для данных конфигураций, соответственно, должны выполняться условия для углов: α ₁3 →π и α ₁₂ →π, что и наблюдается.

На рисунках 3 и 4 изображена динамика падающей капли в двухслойной системе. На рисунке 3 падает капля, обладающая большим поверхностным натяжением: Σ ₁ = 100. Можно заметить, что, как и в статическом случае, в отсутствие гравитации контактные углы на границе трех фаз стремятся к значениям α ₂3 →π, α ₁₂ =α ₁3 → π/2. После того как капля проходит границу двухслойной системы, ее падение продолжается, что не происходит при Σ ₁ = Σ ₂ = Σ 3 = 1 (см. Рис. 4) . Контактные углы также стремятся к конфигурации, аналогичной статической ситуации: α 12 = α 13 = α 23 = 2π/3, однако баланс капиллярных сил в итоге не приводит к отрыву капли, она остается в положении, представленном на последнем кадре рисунка 4.

С помощью численной модели, используемой в работе, также можно исследовать динамику взаимодействия

Рис. 3. Падение капли в двухслойной системе при Σ 1 = 100 , Σ 2 = Σ 3 = 1 , ϕ 1 = - 1000 , ϕ 2 = ϕ 3 =0 в моменты времени t = 0 . 10 , 0 . 20 , 0 . 30 , 0 . 40 , 0 . 43

Рис. 4. Падение капли в двухслойной системе при Σ 1 = Σ 2 = Σ 3 = 1 , ϕ 1 = - 1000 , ϕ 2 = ϕ 3 = 0 в моменты времени t = 0 . 10 , 0 . 23 , 0 . 36 , 0 . 55 , 0 . 80

двух активно движущихся фаз. На рисунках 5 и 6 демонстрируется столкновение двух частиц. Одна из них погружается на дно области (фаза 1 ), другая всплывает ей навстречу (фаза 2 ), обе частицы при этом совершают движение внутри фазы 3 . На рисунке 5 изображены капли со слабым поверхностным натяжением, в результате обе капли на время сцепляются между собой. Это не происходит при сильном поверхностном натяжении, поскольку капиллярные силы стремятся удержать у капель круглую форму даже при их столкновении (см. Рис. 6) . Отметим, что в этом случае поведение капель близко к упругому взаимодействию.

Рис. 5. Столкновение двух различных капель при Σ 1 = Σ 2 = Σ 3 = 1 , ϕ 1 = - 1000 , ϕ 2 = 1000 , ϕ 3 = 0 в моменты времени t = 0 . 17 , 0 . 25 , 0 . 33 , 0 . 60 , 0 . 65

Рис. 6. Столкновение двух различных капель: Σ 1 = 100 , Σ 2 = 100 , Σ 3 = 1 , ϕ 1 = - 1000 , ϕ 2 = 1000 , ϕ 3 =0 в моменты времени t = 0 . 10 , 0 . 18 , 0 . 26 , 0 . 30 , 0 . 42

В качестве примера показываем поле скорости для капель с большим поверхностным натяжением (Рис. 7) , что соответствует полям концентрации рисунка 6. На крайнем слева фрагменте видно, что капли движутся по направлению друг к другу и формируют в зоне движения вихревое течение. В момент столкновения наблюдается один вихрь в центре области, что соответствует общей закрутке капель после соударения. На крайнем справа фрагменте реализуется поле скорости, аналогичное полю левого фрагмента: капли движутся независимо и формируют в зоне движения вихревое течение.

Рис. 7. Поля скорости при столкновении двух различных капель, представленном на рисунке 6

• 5.    Заключение

Предложена и реализована численная трехфазная гидродинамическая модель фазового поля на основе системы уравнений Навье–Стокса и Кана–Хилларда с модификацией химического потенциала путем добавления фиктивной релаксационной производной. Такая стабилизация уменьшает эффективный спектральный радиус итерационной матрицы СЛАУ и позволяет увеличивать шаг по времени примерно в k раз без потери устойчивости полунеявной схемы c сохранием точности при условии kτ → 0.

Проведенные численные эксперименты подтвердили корректность и универсальность предложенного подхода. В статических тестах для различных комбинаций коэффициентов Σi модель воспроизводит ожидаемые контактные углы на стыке трех фаз. Динамические тесты показали, что модель адекватно отображает типичные сценарии: падение капли через границу двухслойной системы (с прохождением или «прилипанием» в зависимости от соотношения коэффициентов поверхностного натяжения) и столкновение двух капель (временная коалесценция при малых Σi и почти упругое отталкивание при больших Σi).

Ограничениями текущей реализации являются: возможное нарушение монотонного убывания свободной энергии при слишком больших k ; требование достаточного разрешения межфазных границ; трудности с обеспечением сходимости решения уравнения Пуассона в условиях сложной динамики на стыке трех фаз.

Полученные в статье результаты продемонстрировали, что разработанный подход обладает хорошим сочетанием устойчивости, точности и вычислительной эффективности в широком диапазоне параметров, в том числе при существенных контрастах плотности ϕ i и поверхностного натяжения, заданных через Σ i . Постоенная модель трехфазной среды допускает дальнейшие модификации, такие как внедрение переменной вязкости и произвольные условия смачиваемости на внешних твердых границах, что позволит представить один из компонентов системы в качестве твердой фазы.

Работа выполнена при поддержке Российского научного фонда, грант № 24-11-00269.