Трехмерная интегральная модель сухого трения для движения прямоугольного корпуса

УДК 539.377: 004.942                                        

Введение. Решение задачи о толстостенной сферической оболочке, испытывающей разные внешние воздействия, приводится в монографиях [1, 2] и ряде научных статей по теории упругости, пластичности, термоупругопластичности [3–9]. Обычно рассматривается случай, когда процесс нагружения является простым.

Задача о толстостенной сферической оболочке является одной из простейших упругопластических задач, когда поля внешних воздействий и внутренних параметров обладают центральной симметрией. В силу центральной симметрии в пластической области выполняется режим полной пластичности. Для идеального пластического тела задача статически определимая, что позволяет ее решить для любых условий пластичности. В монографии [1] приведено наиболее полное решение задачи о сферической оболочке, когда не учитывается зависимость предела пластичности от температуры, а условие пластичности не зависит от первого инварианта тензора напряжений и знака третьего инварианта девиатора напряжений. Рассматриваются случаи только теплового и комбинированного нагружения, когда задана температура на стенках сферы, давление на внутренние стенки, а на внешней стенке давление отсутствует. В работах [10–13] выполнено исследование термоупругопластического состояния разных объектов, а в [3–9] рассмотрен процесс теплового нагружения и разгрузки свободного от внешних усилий шара и полого шара для условия Треска с учетом зависимости предела пластичности от температуры. Решение этой и аналогичных задач представляет интерес, поскольку можно получить аналитическое или частично аналитическое решение для разных математических моделей. Аналитическое решение можно получить при выборе кусочно-линейных функций пластичности [11, 13]. Математическое моделирование объектов позволяет прогнозировать их состояние и поведение в зависимости от значений исходных параметров [14, 15].

Механика

Материалы и методы. Постановка задачи . Рассматривается задача о толстостенной сферической оболочке (полом шаре), испытывающей центрально симметричные внешние воздействия: давление p_b на внешнюю стенку при p = b и давление pa на внутреннюю стенку при p = а . Также рассматривается тепловое воздействие на шар: на границе р = а поддерживается температура Т_а , на границе р = b — температура Tb . Предполагается, что шар проявляет упругие и пластические свойства. Искомыми параметрами состояния в каждой точке шара являются компоненты тензора напряжений, компоненты тензоров деформаций и векторы перемещений. В области упругого состояния упругие деформации являются полными (остаточные деформации отсутствуют).

Основные соотношения . Все соотношения приведены к безразмерному виду. В качестве масштаба длины выбирается внешний радиус шара b . Все величины, имеющие размерность напряжений, отнесены к пределу пластичности при одноосном растяжении к . Масштабная единица для температуры — 1 С.

В силу указанной симметрии внешних воздействий, в сферической системе координат р, 0, ф матрицы компонент тензора напряжений и деформаций будут иметь вид:

	ч	0	0 ^		Ч	0	0 '
(о) =	0	ст0	0	, (е) =	0	£0	0
	1 0	0	ст		1 0	0	£ф >

В данном случае выполняются равенства н0 = аф, е0 = еф.

Если функции пластичности не зависят от первого инварианта тензора напряжений и знака третьего инварианта девиатора напряжений, то при решении задачи о шаре функции пластичности будут приводиться к виду:

• f =1 ° 0 -° р 1= ^к .

Рассмотрим условие пластичности:

^((ст -5ep)w + 2(ст-5еp)w)w f (CT CT £ P £ P ) = pp—07

• ^{7    p , 0} , ^{p , 0}                ^ + n (1 + а )^1/ m

п (( | ст-ст -5 ( s ^p -e ^p)\ m + а ( ст -ст-5 ( е ^p -e ^p ) m ) m

0 p         0 p                p 0p 0

Чпа+оГ”             ", где ep, ep — компоненты тензора пластических деформаций; T — температура.

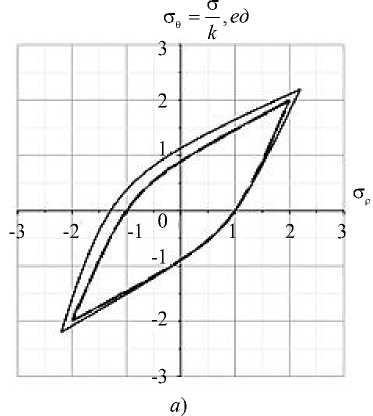
Когда параметры имеют значения: <; = 0, п = 1,5 = 0, а = 0, m = 1, ц = 0, к = к0, из условия (2) следует условие (1). На рис. 1 в плоскости CTp, ст0 представлены кривые пластичности, определяемые по формуле (2) для разных значений числовых коэффициентов в функции пластичности.

= к ’ ед

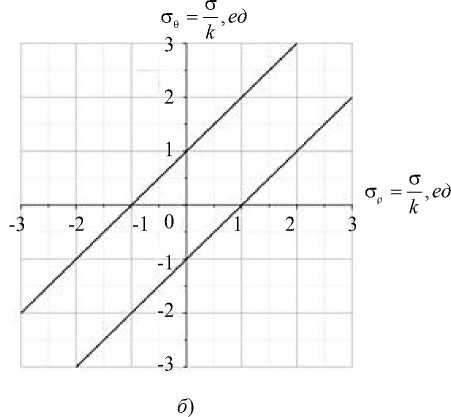
Рис. 1. Кривые пластичности: а — для параметров: <; = 0,2; w = 2; п = 0,5; 5 = 0; m = 3; к = 1; сплошная линия а = 0,5; пунктирная линия а = 0; б — для параметров: а = 0; ^ = 0; 5 = 0; к = 1

Результаты, представленные на рис. 1, показывают, что при учете первого инварианта тензора напряжений радиальное и окружное напряжения, когда точка шара находится в упругом состоянии, могут изменяться в ограниченном диапазоне. Соответственно давление на границы шара также должно быть ограниченным. Когда первый инвариант в условии пластичности не учитывается, упругое состояние возможно для любого значения давления на границах шара, но ограничен перепад давления Ap = pa - pb. Учет знака третьего инварианта девиатора напряжений, как отмечалось выше, влияет на значения пределов пластичности.

Если значения параметров состояния ор,ои определяют точку области, ограниченную кривой пластичности, принимается, что определяющими уравнениями, связывающими напряжения и деформации, являются соотношения закона Дюамеля-Неймана [1,2]:

E е„ = (1 -v)o„-vo + E a T , E е = о - 2vo„ + E а T ,                         (3)

• и                   и          р                         р р            и

• где модуль Юнга E и коэффициент Пуассона v — константы.

Если параметры состояния ор, ои определяют точки на кривой пластичности, то принимается аддитивное представление полных деформаций через обратимые и необратимые деформации:

ep   ep еи   еи + еи ,   °р   °р + °р •

Полные деформации определяются через перемещения по формулам:

е

и

u

,

р

ер

du d р

Полные деформации связаны условием совместности деформаций:

d е r - + е„-е = 0. dr 6 р

Приращения необратимых деформаций связаны с напряжениями нормальным законом:

d еР = d еР df / dOu df / дОр •

Соотношение (7) при выборе нелинейных функций пластичности в общем случае неинтегрируемое [16]. В квазистатическом приближении напряжения должны удовлетворять уравнению равновесия:

d о р      2(gp-g ) = 0.                                          (8)

d р

Эквивалентное напряжение. Эквивалентное напряжение — это выпуклые изотропные скалярные функции тензора напряжений. В частных случаях термин «эквивалентное напряжение» является синонимом других терминов, например, «интенсивность напряжений» [17]. В настоящей работе эквивалентное напряжение совпадает с функцией пластичности. В этом случае на упругопластической границе эквивалентное напряжение не будет иметь разрыва.

Поле температур. Поле температур в шаре находится из решения краевой задачи [1]:

Г d ² t dT , р--- + 2— = 0, <  d р ²      d р                                                             (9)

T | = T , T | = T .

Iр= a       a ,        1р= b b

Решение задачи (9) представим в виде:

T = T + - ^{a A} T -1 b - 1 1 , A T = T - T .                                  (10)

b                               ,               a b

( b - a ) ^p J

Упругая область. В области упругого состояния полого шара формулы для напряжений имеют вид:

, В X        . В X , abEaAT о = A +---, о = A----, X =-----------.

^р        р ³ р ^u       2 р ³ 2 р         (1 -v )( b - a )

Пластическая область. Выберем условия (1). Рассмотрим случай только теплового воздействия (10).

Тогда пластическая область будет зарождаться на внутренней границе оболочки при условии [1]:

Механика

0 = _E a_| A t h^ ^{2 a} ‘ ^{+ ab +} b ^:) k .

(1 -v )         ¹       b ( a + 2 b )

Обозначим через с , — радиус упругопластической границы р = с ₁. В процессе нагружения, когда в > в , , пластическая область a < р <  с 1 увеличивается. При выборе условия (1) напряжения в области a < р <  с 1 вычисляются по формулам:

Op) = 2к k ln(P / a),  Gp) = Gp) +Ki k, к = sign (g6—gp), где к1 = sign(g6 — gp ) |p=с . Если AT > 0, то к1 = —1, если AT < 0, то к1 = +1.

Если область с1 < р < b остается упругой, то величины A , B и радиус упругопластической границы с1 определяются из условий непрерывности напряжений на упругопластической границе и граничного условия g |р=b = 0. Так, если A и B определяются только упругопластической границе, то имеют место выражения:

^Г Г c j ^{1 j} X

A = 2 к₁ k I ln I ¹ I + — 1+-- ,

( ( a J 3 J 3 c ₁

из условий непрерывности напряжений на

_R X с 2 2 . 3 B = — к, kc, .

Уравнение для вычисления с ₁ будет иметь вид:

„ , [, Г c. j    12

2 к. k In 1 +

1 I I a J   33

^^^^^^B

+ | —+— ¹ |x = 0. ( 3c₁ 3 b ³ b J

c ₁

Если A и B определяются из условий непрерывности напряжений на упругопластической границе и условия g |_p = b = 0 , то имеют место выражения:

A = I 1 —

c 2 jX 2 к kc 3        X c .2    2

—    + —¹—^L, B = —¹---к kc ,^.

3 b ² J b 3 b³                3     3 ^{1 1}

Выбор формул (11) или (13) влияет на шаги алгоритма решения задачи, но не влияет на окончательные результаты.

На границе р = b будет зарождаться вторая пластическая область, если выполняется условие:

^(G 6 — ^G p )| p= b =^к 2 ^k , ^к 2 = ^—к 1 ^.

Для определения значения A T = A T , когда выполняется условие (14), необходимо решить совместно систему уравнений (12), (14). Поскольку параметр в в уравнения (13) и (1) входит линейно, то можно получить отдельно уравнение для определения радиуса упругопластической границы:

2 к₁ k ln I ' X 4'•( b - ^ =1 ( a J         3( b + c ₁) bc₁

—

b 2 ) = 0,

а также формулу для вычисления параметра в :

_в = _в = ^{2 k} 0^{( к} 2 b ³ — ^к 1 ^c 3⁾⁽ b — a ) ^{р р 2}         ( b² — c 2) ab

.

В процессе дальнейшего нагружения, когда выполняется неравенство в > в ₂, область шара c ₂ < р <  b переходит в пластическое состояние на границе р = b .

Полый шар при тепловом воздействии. Учет упрочнения материала. Рассмотрим случай, когда условие пластичности имеет вид:

^{f( g} p , ^Ge , e p , e ^p) = 1 ^Ge ^{— g} p ^{— 8 (} e ^{p —}<  ) = ^{k .}

Если до нагружения в шаре остаточные деформации отсутствуют, то в результате теплового нагрева пластическая зона будет зарождаться на внутренней границе р = a , когда выполняются условия (15), (16). При дальнейшем нагружении образуется пластическая область a < р <  c₁ . Для нахождения напряжений в этой области надо из системы уравнений (3–6), (8), (17) получить соответствующие уравнения:

р ²

G

d ²°р d p ²

d g

+ 4p—^ — dp 1 + 38(1 — v)

8 abE aA T j = 0 p ( b — a ) J ,

P d ^g ---+ g .

2 d p     ^p

Решение системы (18) запишем в виде:

Gp

Ge

1 + 3 8 (1 — v )

1 + 3 8 (1 — v )

| 2 k In p

3 8 abE aA T

^^^^^^B

p ( b — a ) J

3 8 abE aA T k + 2 k In p-- 2 p ( b — a )

C ₁

⁺ 2 ,

p

V ^C + C 2 .

J 2 p

Величины C1, C2, входящие в формулы (19), определяются из граничного условия ср |р=a = 0 и условий отсутствия пластических деформаций на упругопластической границе р = с1:

C = 2 к ( k - k ) c 3 - 3 E a N.c 2 , 1                1                 3       1                          3 1

C = 2к. k, ln a + 2             1 3

2 к. ( k - k, ) c 3   E a N

1 v        3 X 1 +           6

3 a ³

c ₁

a

—

a

3 ab A T

.

N_s =---------------

³    (1 + 3 3 (1 -v ))( b - a )

В результате подстановки (20) в (19) получим:

c =-------- р 1 + 33(1 -v)

2 к 1 k In -^P + a

3 3 abE aA T f 1  1

--—

-

2 к. kc ³   3 abc 2 E aA T

11        1

b - a

1 a ³

-

С =-------

⁶ 1 + 3 3 (1 -v )

-

к 1 kc 3

b - a

a р

P ³

2к. kc 3 + —¹—^L

-

3    ( a ³    р ³

,

к 1 k + 2 к , k In -^р +

3 abc ² E aA T ¥ 2

2( b - a )

a

3 3 abE aA T f 1   1

a

P

b - a

к kc ³ + — -

---— a 2 р)

a р

Из решения упругой задачи следует: если A T >  0, то к 1 =

—

Учет пластической сжимаемости. Рассмотрим линейной относительно компонентов тензора напряжений:

1; если A T <  0, то к 1 = + 1.

случай, когда функция пластичности является

? ^{(2 С}6^+Ср ) ^{+ к ( с}б^-ср ) + П ^{( С}6 ^к = sign ⁽ С б^- С р ).

-

С р ) = k о (1 -X T ),

Условие пластичности (21) можно представить в виде: аС б +Р^ р = ^{k (1} -X ^T ), a = 2 g + к-n , P = д-к + п .

С учетом введенных обозначений, задачу:

для определения напряжений

в пластической области получаем

Решение задачи (22) имеет вид:

С

^- Pa ⁺

( M x - 1) k о

c6

-

P

a

-

a^+Pc = k (1 -X T), d С р      2(Ср-Сб) = 0, d р c | = - p .

р 1р= a     ^p a

2 Nk ₀ ) ¥Y^+2P/^a    M - 1

X 0        ^a                X____

a + P     a ( a + 2 P ) )(р

-

2 N ,

a + P   р ( a + 2 P )

k 0 ,

( M - 1) k   2 Nk Y a Y^+2P / “

■ P +—x------+----X — II I a a + P     a (a + 2P) )(р)

-

M - 1 N

——+--X— k, a + P р(a + 2P) J 0

a AT     ab A T где введены обозначения: M = 1, -    , N =     , M =xM, N =XN • b - a       b - a     X          X

Для получения правильного результата из (20), когда, например, a + P = 0, надо выполнить предельный переход при решении (22). Более просто получить правильный результат можно непосредственно в (23), при этом учесть, чтобы выполнялось условие a + P = 0 . В этом случае g = 0, поэтому получим:

• ^{2 k} o I             ^р I ¹¹ II

c = —⁰ (1 - M ) ln +   - N - p ,

X                                 X          a a (          a (р a J J

(                                     I

С б = -° I (1 - M X )(1 + In ^р ) + N x| - - - I I- Pa • a (              a      (р a))

В процессе нагружения пластическая зона зарождается на границе р = a , когда выполняется условие:

Механика

A T = к o (1 -x T b )/ | k o X —

(2 ^ + к - n )( a + 2 b ) bE a 2(1 -v )( a ² + ab + b ²)

Результаты исследования. На рис. 2 приведены графики напряжений и годографов вектора напряжений, когда область шара, соответствующая условию а < р < с1, находится в пластическом состоянии, а области шара, соответствующая условию с1 < р < b, — в упругом состоянии.

k ’ ед

0,5

-0,5

-1

р = r- , ед b

a )

---- СТ------- СТ

р

------- СТ eq

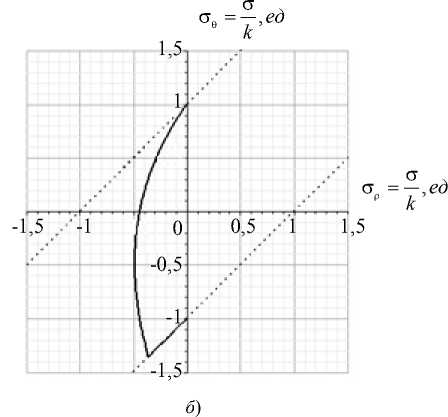
Рис. 2. Графики напряжений ( a ) и годографов вектора напряжений ( б ) при значениях параметров: к = 1; v = 0,3; а = 0,5; b = 1; A T = 170; с = 0,57

На рис. 3 приведены графики напряжений и годографов вектора напряжений, когда области шара, соответствующие условиям а < р < с1 и с2 < р < b, находятся в пластическом состоянии, а область шара,

соответствующая условию с 1 < р <  с ₂, — в упругом состоянии.

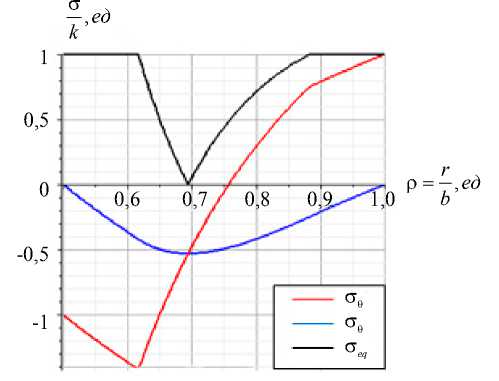
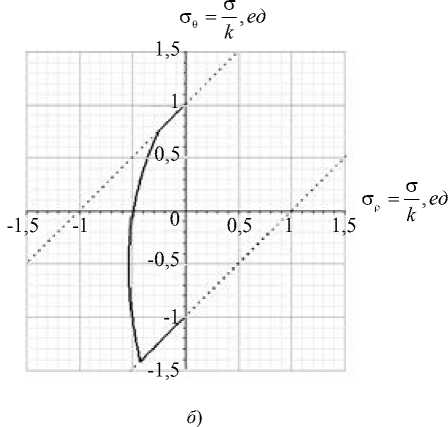
Рис. 3. Графики напряжений ( a ) и годографов вектора напряжений ( б ) при значениях параметров: v = 0,3; а = 0,5; A T = 270; с 1 = 0,62; с 2 = 0,88

На рис. 4 приведены графики напряжений и годографов вектора напряжений, когда область шара, соответствующая условию а < р <  с 1 , находится в пластическом состоянии, а область шара, соответствующая условию с 1 < р <  b , — в упругом состоянии.

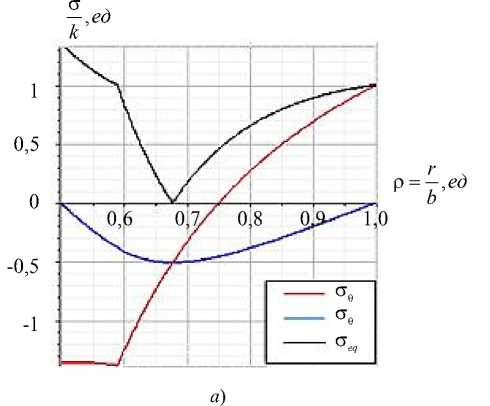
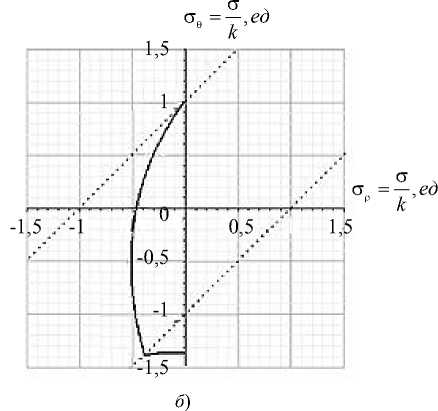
Рис. 4. Графики напряжений ( a ) и годографов вектора напряжений ( б ) при значениях параметров: ν= 0,3; a = 0,5; ∆ T = 215; с ₁ = 0,58

На рис. 5 приведены графики напряжений и годографов вектора напряжений, когда области шара, соответствующие условиям a≤ρ≤c1 и c2 ≤ρ≤b, находятся в пластическом состоянии, а область шара, соответствующая условию c1≤ρ≤c2, — в упругом состоянии.

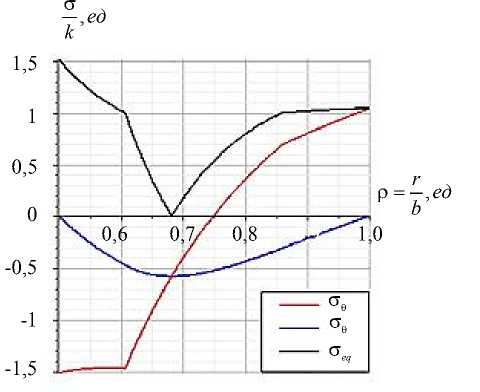
a)

Рис. 5. Графики напряжений ( a ) и годографов вектора напряжений ( б ) при значениях параметров: ν= 0,3; a = 0,5; ∆ T = 270; с ₁ = 0,61; с ₂ = 0,86

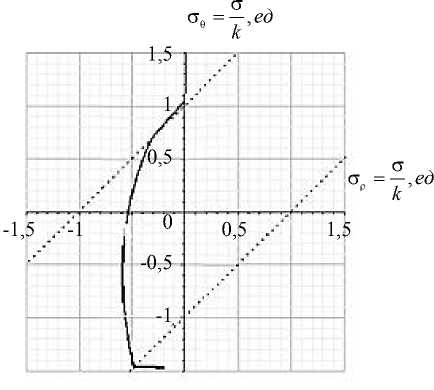
б )

На рис. 6 приведены графики напряжений и годографов вектора напряжений, когда области шара, соответствующие условиям a ≤ρ≤ c ₁ и c ₂ ≤ρ≤ b , находятся в пластическом состоянии, а область шара, соответствующая условию c ₁ ≤ρ≤ c ₂— в упругом состоянии.

Механика

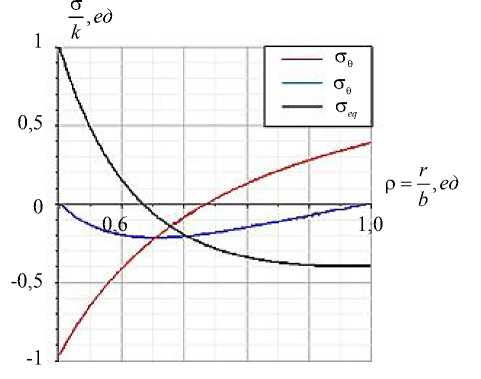
a )

Рис. 6. Графики напряжений ( a ) и годографов вектора напряжений ( б )

при значениях параметров: ν=0,3; a =0,5; ∆ T =79; ς =0,1; η =0,1; E α =0,012; χ=0,0017

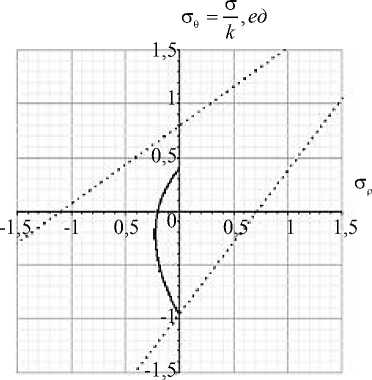
б )

Обсуждение и заключения. Результаты вычислений показывают, что в данной постановке задачи, когда имеет место только тепловое воздействие, полый шар полностью не переходит в пластическое состояние (рис. 2–6). Упрочнение приводит к увеличению эквивалентного напряжения в пластической области и уменьшению радиуса упругопластической границы (рис. 4, 5). Упругая область в процессе нагружения не может полностью исчезнуть. Пластическая сжимаемость и зависимость предела пластичности от температуры оказывают существенное влияние на напряженное состояние полого шара (рис. 6).