Трехмерная симметричная задача протекания для уравнений Навье - Стокса

Постановка задачи

па.

ца.

Рассматривается стационарное течение несжимаемой вязкой жидкости в области О ти-сферического слоя с внутренней границей Г1 и внешней границей Г2 класса Липши-Предположим для простоты, что поверхности Г1 и Г2 являются звездными относи-

-

-

-

тельно начала координат. Обозначим через г, ф, z цилиндрические координаты, а через и, v, w —соответствующие проекции вектора линдрических координатах имеют вид

скорости u. Уравнения Навье - Стокса в ци-

∂u	v ∂u	∂u	v 2
и —-- +	— --	+ w    —	• — =
∂r	r ∂φ	∂z	r
∂v	v ∂v	∂v	uv
и Д--+		+ w   +	- =
∂r	r ∂φ	∂z	r

-

-

1 =p + V (А v +2 du r ∂ φ            r2 ∂ φ dp+v (а и—a dv ∂ r             r2 ∂ φ

∂w u ∂r r ∂φ

∂w v

+ w

-

2 ди

r ² ∂ φ

Здесь p — отношение

и ) >

-

V ) >

∂u   u

∂r   r

∂w ∂z

∂v

+ r ∂φ

+

-

∂p

+ V А w, ∂z

∂w

= 0 • ∂z

давления к плотности жидкости, v = const >

— коэффициент

кинематической вязкости, А

-

оператор Лапласа в цилиндрических координатах,

А д ² q   1 dq   1 dq   д ² q

.

^q ∂ r ²    r ∂ r   r ² ∂ φ ²    ∂ z ²

Для системы (1) задаются краевые условия u = ai(x), x G Гi, i = 1, 2,                                      (2)

где функции ai G W1 /2’2 (Гi) удовлетворяют условию j a1 • n1 d Г1 =

Γ1

У a 2 • П 2 d Г2 = F

Γ2

(n i обозначает единичный вектор в пешней нормали к поверхности Г i ). Задача, (1)-(3) представляет пример задачи протекания для уравнений Навье-Стокса. Неизвестно до сих пор, имеет ли эта задача решение, если величина F не является малой. Данная работа содержит достаточные условия ее разрешимости.

• 2.    Лемма Хопфа

Рассмотрим более общую ситуацию. Предположим, что граница д П области П состоит из N связных компонент Г i: д П = Г1 U Г2 U ... U Г n и Г i П Г j = 0 , i = j. Требуется найти решение u , p уравнений Навье-Стокса,

—V Au + u • Vu + Vp = 0, x G П,(1)

div u = 0, x G П,(6)

удовлетворяющее условию u = a, x G дП.(6)

Вследствие уравнения неразрывности (1.2), функция а должна удовлетворять условию

У а • n dS = 0,(7)

∂Ω где n - единичный вектор внешней нормали кд П, выражающему равенство нулю общего потока несжимаемой жидкости через границу области течения. Обозначим через Fi поток вектора а через поверхность Гi. Предположим, что выполнено более сильное условие, чем (2), а. именно,

У а • n dS = Fi = 0 , i = 1 , ...,N.

Γ i

При выполнении этого условия задача. (4)-(6) имеет, по крайней мере, одно решение [1]. В указанной работе Ж. Лерэ этот результат получен рассуждением от противного. Э. Хопф [2] получил априорную оценку решения. Следуя [3], определим пространство Н(П) как замыкание множества вектор-функций £ G C0”(П), div^ = 0, в норме интеграла Дирихле llVwIIL2(Q) = / 52 (дwi/дxk)2dx-

_Ω i, k =1

Лемма 1. [2] Предполоэюим, что граница д П области П принадлежат классу Липшица и что заданное на границе векторное поле а принадлежаит классу W ¹ / ^{2 , 2}( д П). Если

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ выполнено условие (8), то для любого е > 0 существует соленоидальное продолжение b (х, е) G W1,2 (И) граничного поля а в областъ И такое, что b · w · ∇w d x

Ω

< ^е I I w I I W1 1 , 2 (q)

V w G Н (И) .

Доказательство леммы изложено в монографии О.А. Ладыженской [3]. Ключевую роль в этом доказательстве играет тот факт, что при выполнении условия (8) возможно продолжение векторного поля а в область И в виде В =rot D, D G W ^{2 ,2} (И). Затем это продолжение подправляется с помощью срезающей функции Хопфа £ ( х, е ), зависящей от параметра е >  0. так что A = rot( £ ( х, е ) D ( х )) .

Эффективное построение векторного поля В =rot D в случае гладких поверхностей Г i предложено X. Фуджита [4] и Р. Финном [5]. Ими же установлена разрешимость трехмерной задачи протекания в случае малых значений потоков Fi. Впоследствии X.Фуджита и X. Моримото [6] доказали аналогичный результат для течений, мало отличающихся от потенциальных. М.В. Коробков, К. Пилецкас и Р. Руссо установили разрешимость плоской и осесимметричной задачи протекания без ограничений на величину потоков. Обзор их результатов имеется в статье [7].

Оказывается, что достаточное условие (8) для существования соленоидального продолжения А ( х, е ) граничного поля а в область И, для которого неравенство (4) выполнено с любым е >  0, является и необходимым. Первый пример, доказывающий этот факт, был построен в работе А. Такешита [8]. Впоследствии появились и другие примеры (они приведены в обзоре [7]).

С помощью (9) получаются оценки | |u|| _w 1 , 2 (q) < C, H^pH^ 2 (q) < C для всех возможных решений u , p задачи (4)-(6), где положительная постоянная C зависит от нормы | |а|| ^ 1 / 2 , 2( д q) ¹¹ константы Липшица фупкщш. параметризующих поверхность д И [3]. Возникает вопрос: как задать продолжение вектора а в область И при выполнении лишь необходимого условия (7), чтобы неравенство (9) имело место? В работах Л.И. Сазонова [9] и X. Фуджита [10] дается ответ на этот вопрос в случае плоских симметричных векторных полей. В работе автора [И] аналогичная конструкция предложена для осесимметричных векторных полей в трехмерном пространстве.

• 3.    Симметричные решения уравнений Навье - Стокса

• 4.    Модификация срезающей функции

Хорошо известно, что уравнения Навье-Стокса допускают бесконечномерную псевдогруппу Ли (см., например, [12, 13] и цитируемую там литературу). Это их свойство является источником точных решений данных уравнений и имеет ряд других приложений. Между тем, эти уравнения обладают и дискретными симметриями, в частности, симметриями по отношению к отражениям. Например, система (4), (5) обладает решениями, в которых компоненты и i, и 2 вектора скороети и давление p являются четными функциями х з. а компопепта и з является печетной функцией х з ( и^ обозначает проектщто вектора и па ось хк декартовой системы ко ординат в пространстве R³). В плоском случае существуют симметричные решения этой системы, в которых и i и p — четные функции переменной х 2, а и 2 — нечетная функция этой переменной.

Предположим, что область И G R2 имеет ось симметрии х2 = 0, и что заданное на ее границе векторное поле а = (ai, a2) обладает свойством симметрии в указанном выше смысле. Кроме того, пусть ось симметрии пересекает каждую из связных компонент Гi границы области И. Если вектор а и поверхность д И удовлетворяют условиям Леммы 1, то задача протекания для уравнений Навье-Стокса (5) - (7) имеет, по крайней мере, одно обобщенное решение, в котором u Е W1,2(П) и Vp Е L2(И). Впервые этот результат был установлен Ч.Дж. Эмиком [14] и независимо Л.И. Сазоновым [9] рассуждением от противного. В этих работах симметричная область И была криволинейным кольцом с внутренней границей Г и внешней границей Г2. Вероятно, Л.И. Сазонов не знал о работе Эмика, но он доказал теорему существования более простым способом, используя понятие виртуальной дрены. Сам этот термин был введен Фуджита [10], который также получил априорную оценку нормы ||u||w 1,2(q) в плоской симметричной задаче протекания и на ее основе дал конструктивное доказательство теоремы существования.

Как уже отмечалось, соленоидальное продолжение заданного на поверхности д И векторного поля а внутрь области И в виде ротора некоторой функции невозможно, если нарушено условие (8). Идея виртуальной дрены состоит в представлении желаемого продолжения в виде суммы b = c + d, где функция d удовлетворяет условию нулевых частных расходов

У d • n dS = 0 , i = 1 ,...,N, г i

а носитель функции c = ( c i( x 2) , 0) сосредоточен в узкой полоске, примыкающей к оси симметрии x 1. Это слагаемое в сумме b = c + d обеспечивает перетекание жидкости с одной компоненты границы области И на другую, причем его вклад в выражение в левой части неравенства, аналогичного (9), оценивается сверху величиной C ^ N | Fi | . Функция c i( x 2) также выражается в терминах срезающей функции, подобной функции Хопфа. Элегантная конструкция такой функции предложена Фуджита [10]. В следующем разделе мы строим модификацию срезающей функции Хопфа - Фуджита, позволяющую доказать аналог неравенства (9) для трехмерных симметричных соленоидальных векторных полей в области типа сферического слоя, которые удовлетворяют необходимому условию (7).

Определим семейство функций s _k ( t ) с помощью соотношений

ςκ

I ^к |

Е C2^,Lip (R); S k >  0 , S k ( - t ) = S k ( t ) , t Е R; S k <  ¹ (0 < t <  то ) ,

2 ,                    .                ,                      .                1 ,                   1 t ,                            к.

<   (0 то ) , S k = 0(1 <  t <  то ) , S k = 7 ( к <  t <  7) , S k = 0(0 <  t <  -) .

t²                                                   t              2                       2

По сравнению с конструкцией срезающей функции, предложенной Фуджита, здесь добавлено ограничение на величину | s ‘ | и требование, чтобы s _k = const, если | t | < к/ 2. Полагая Y _к = J-^ S_K ( t ) dt = J - 1 S _k ( t ) dt , мы замечаем, что y _k >  2 J1 / ² dt — то , ес ли к — 0. Введем вспомогательную функцию n ( t ) = n ( t ; 6, к ) посредством равенства

П ⁽ t )

_δ ^t , t ∈ R ,

где постоянная 6 >  0 достаточно мала, но фиксирована. Из (И),

(12) вытекают оценки

, x 11 6

⁰ <  n ⁽ t ) <          =

γ δt которые влекут соотношения

γ

t,

0 <  | n ( t ) I <

γ

_2 6 2

δ ² t ²

— ^2 ’ ⁽ t = ⁰⁾ ’ γ t

sup | t I n ⁽ t ) t

→

0 , sup t ² | П ( t ) | —

0 ,

если

к —— +0 .

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

Условия (11) будут выполнены при следующем выборе функции у_к:

κ

^{S k} = 24 К ° - t - 2; ^{S k} =

Ф - ¹⁶ ( t - ¹ V +6 ( t - ¹ Yl ," - t - К ; к 24    3 к 2          к 2      ’ 2 ” ” ’

S k = t, к - t - |; S k = 112(1 - t )³ - 32°(1 - t )⁴ + 256(1 - t )⁵ , | - t - 1 .

• 5.    Формулировка основного результата

Вернемся к задаче (1) - (3). Пусть существует функция b такая, что div b = °, x Е И,                                       (15)

b = ai , x Е Г i, i = 1 , 2 . (1G)

Ниже будем рассматривать функции b из пространства Соболева W ^{1 , 2} (И). В этом случае уравнение (15) выполняется в смысле распределений. Далее считается, что область И имеет плоскость симметрии z = °. Предположим, что проекции векторов ai , a2 на оси г, ф цилиндрической системы координат являются четными функциями переменной z. а их проекции на ось z - нечетные функции z. В этих условиях можно рассчитывать на то, что задача (1)-(3) имеет симметричное решение, в котором проекции вектора скорости u на оси г, ф цилиндрической системы координат и давление p будут четными функциями переменной z. а проакция u на ось z будет нечетной функцией z.

Обозначим через H _s (И) подпространство пространства Н(И), образованное вектор-функциями, симметричными в указанном выше смысле. Функция u называется обобщенным решением задачи (1) - (3), если u = U + b , где U Е H _s (И), и выполнено интегральное тождество

ν

∇ U · ∇ηdx

Ω

j (U + b ) -V )

Ω

η· U dx

j (U -V ) n

Ω

b dx =

= -v

j V b -Vn dx +

Ω

У (b -V ) n - b dx V n Е H _s (И) .

Ω

Основным результатом работы является

Лемма 2. Предположим, что граница дИ = Г1 U Г2 области И принадлежит классу Липшица и что заданные на границе функции a1, а2 принадлежат классу W1 /2,2(дИ). Пусть выполнены указанные выше предположения относительно симметрии области И и функций a1, а2. Если, сверх того, выполнено условие j a1 - n1 d Г1 =

Γ1

У a₂ - n₂ d Г 2 = F >  °

Γ2

то имеет место априорная оценка hVUh22(Q) - C.                                     (19)

обобщенного решения задачи (1) - (3).

• 6.    Доказательство Леммы 2

Положим в тождестве (10) п = U- Это дает:

ν ∇ U · ∇ U dx - I b - (U - V ) U dx =

— V jV b -V U dx + jb - (b -V ) - U dx. (20)

Ω

Ω

По аналогии с работой Фуджита [10], мы строим вектор-функцию b, удовлетворяющую соотношениям (15), (16), в виде b = c + d, где

F

c = ⁽ cr, o , o) , cr = —п ⁽ z )

(виртуальная дрена), а функция d удовлетворяет условию нулевых частных расходов (10) с N = 2. На основании леммы Хопфа, мы в состоянии выбрать d таким образом, чтобы обеспечить выполнение неравенства | I2 | <  | ||V U h L 2 (q) , V U e H s (Q)

У d - U -V U dx <  | hV U h L 2_(Q) , V U e H s (Q) .

Q

(Выбором величины - мы распорядимся позже). Основная трудность состоит в оценке выражения

- У c - (U - V ) U dx = 2 П У V drdфdz - ΩΩ

- Г / п ( U^U + ^V |U + WOU ) drdфdz = 1 1 + 1 2 ,

2 n or r Оф oz

Ω возникающего при подстановке выражения для функции b в левую часть равенства (20). (Здесь U, V, W — проекции вектора u на соответствующие оси цилиндрической системы координат). При выводе соотношения (23) были использованы уравнения (1) и равенства (21). Если F > 0, то величина 11 неотрицательна. Покажем, что за счет подходящего выбора функции п можно обеспечить выполнение неравенства

I I 2 |< | hV U h L ₂(_Q) , V U e H s (Q) .

Учитывая уравнение неразрывности, условия симметрии и тот факт, что функции U, V, W oбpaщaютcя в нуль на границе области Q, а функция п ( z ) обращается в нуль при | z | >  5, мы после интегрирования по частям приходим к соотношению:

I 2 =

— [ [ п‘ ( z ) UW — — п ( z ) U 2] drdфdz■ 2 tv                    r

Ω

Введем обозначения

I з = У п‘ ( z ) UWdrdфdz, I4 = У — п ( z ) U2drdфdz.

ΩΩ

Неравенство (24) будет доказано, если мы установим, что

Fε   Fε

I I з | <  4 hV U h L ₂(_Q) , — I I 4 1 < - hV U h L ₂(_Q) , V U e H s (Q) .

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

Рассмотрим четную функцию х ( z ) € C^ (R) ^со следующими свойствами: х >  0 , X <  0 , z € R+; х (0) = 1 , х = 0 , z >  к ² . Определим функции U 1 11 U ₂ соотношениями

U 1 = ^[1 - х ^{( z )]} U ⁽ r, Ф, ^z ) , U 2 = х ^{( z} ) U ⁽ г, Ф, ^z ) .                    (28)

Очевидно, что

U ( г, ф, z ) = U 1 + U 2 , U i( г, ф, 0) = 0 , U 2 = 0 , | z | >  к ² .                (29)

Далее будем считать, что к <  1 / 2.

Определенное первым из равенств (26) выражение I з представимо в виде

I 3

= j П‘ ^{( z} )

Ω

U 1 Wdr dфdz +

J П‘ ^{( z} )

Ω

U 2 W d r d φ d z

У п‘ ( z ) U 1 Wdrdфdz

Ω

(здесь мы использовали последнее из равенств (21) и тот факт, что п‘ = 0, если | z | <  к/ 2). Из (29), второго равенства (28), условия W ( г, ф, 0) = 0 и неравенства Харди вытекают оценки:

1 1 з |< Д2 I п Д^ - И drdpdz < | z |           | z |

Ω

U ² 2^{1 z}

Ω

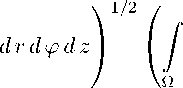
W ²

drdφdz z ²

1 / 2

≤

< C 1 SI T p⁽ z ^{2 1} X ^|) || U 1 \\ _H 1(_Q) I I W Ь _я 1(_Q) <  C 1 sup⁽ z ^{2 1} X ^{|) |V} U I I ² 2(_Q)    ,          (31)

где постоянная C1 > 0 зависит только от геометрии области. На основании (19) мы можем выбрать параметр к столь малым, что FC1 (2 п)_ 1 sup (z2 |n‘|) < е/4 (при бспыпих F этот z параметр имеет порядок exp(-aF), a = const > 0). Итак, за счет выбора параметра к мы добились выполнения первого из неравенств (27). Докажем второе неравенство (27). Представим величину 14 в виде суммы трех интегралов, 14 = 15 + 16 + 17, где

1 5 = / — n ( z ) U 2 drdфdz, r ¹

Ω

1 6 = j"_rn ( z )

Ω

U 1 U 2 d r d φ d z,

1 7 = / — n ( z ) U 2 drdфdz. r ²

Ω

Учитывая, что U 1( r, ф, 0) = 0, и рассуждая так же, как при получении оценки (23), мы

убеждаемся, что за счет выбора малого параметра к можно обеспечить неравенства

F 1 1 <  е IV U I L ₂(_Q) , F | 1 б | <  е |V U I L ₂(_Q) , V U € H _s (И) .        (33)

2 п       12              2 п 12

Для получения оценки величины | I 7 1 воспользуемся неравенствами Ладыженской и Юнга:

U 71 <  А

ρ ²

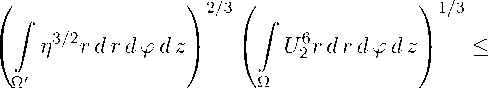
<    р 2    ^{|U 2} \ h 1(Q)

2 / 3

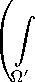
n ^{3 / 2} r d r d ф d z

где р = dist (Г1 , { 0 } ). а область П ‘ есть переселеппе области П и с.тоя | z | < к2 Теперь заметим, что функция у_к ( t ) допускает отщнку сверху, д_к <  a/к при всех t Е R, а величина Y_K оценивается снизу, y _k Д b ln (1 /к ) (можно взять a = 2 , b = 1). Отсюда и из определения (18) функции п получается неравенство

_{δ κ} 1 / 2

п ³ / ² rdrdydz <  C2           ,                      (36)

J                          [ln(1 /к )]³ / ²

Ω′ где постоянная C2 > 0 зависит лишь от области П, а величина 5 фиксирована. Учитывая неравенства (26), (27) и выбирая параметр к достаточно малым, мы приходим к оценке

F- | I 7 1 <  ^ |V U || ² ₂(_Q) , V U Е H s (П) .                        (36)

2 п 12

Суммируя неравенства (33) и (34), мы заключаем справедливость второго неравенства (27), откуда следует оценка (24). Вместе с соотношением (23) и неравенством (22), эта оценка позволяет получить искомую априорную оценку нормы || V U|| _L 2(q), исходя из равенства (20). Это завершает доказательство Леммы 2.

• 7.    Заключительные замечания

Прямым следствием оценки интеграла Дирихле решения задачи (1) - (3) является

Теорема 1. Пусть выполнены условия Леммы 2. Тогда существует обобщенное решение v, p задачи (1) - (3), в котором v Е W ^{1 , 2} (П) , Vp Е L ²(П), и справедлива оценка (19).

Доказательство Теоремы следует стандартным схемам, изложенным в [3, 4, 5]; оно здесь не приводится. Вопрос о единственности решений стационарных задач для уравнений Навье - Стокса очень сложен. Это подтверждается следующим примером. Пусть П Е R² — круговое кольцо, r 1 < r = ( x 1 + x 2)1 / ² < r ₂. На границе П задаются условия и = (2 nri ) ~ ¹ F, v = 0 , r = ri, i = 1 , 2, где F = const, a u и v — радиальная и окружная компоненты вектора скорости в полярной системе координат. Тогда задача протекания имеет решение и = (2 nr ) ~ ¹ F, v = 0. Оно описывает радиальное течение, порожденное источником или стоком интенсивности F , расположенным в начале координат. Теорема единственности решения задачи протекания сквозь круговое кольцо доказана лишь в случае малых чисел Рейнольдса Re = F/v. Для произвольных значений параметра Re удается доказать только изолированность этого решения [15].

Что касается гладкости обобщенного решения задачи (1) - (3), то она повышается с повышением гладкости поверхностей Г i и определенных на них функций a i ( i = 1 , 2). Так, если поверхности Г i принадлежат классу Гёльдера C ^{2+ а} (0 < а <  1) и a i Е C ^{2+ а} (Г i ), то справедливы включения u Е C ^{2+ а} (П) , V p Е C^а (П) [3].

Результаты работы допускают обобщение на случай симметричных в смысле п. 5 решений задачи протекания, в которых число связных компонент границы N >  2. Однако обременительное условие положительности потоков (в рассмотренном в статье случае это условие F >  0) снять не удается. Здесь уместно провести аналогию с другими задачами, в которых течения, порожденные источниками и стоками, имеют разные качественные свойства. Это хорошо проявляется в решении классической задачи об автомодельном течении в плоском диффузоре [16]. Другой пример демонстрирует рассмотренная в [17] задача об осесимметричном течении в области, ограниченной поверхностью вращения и пересекающей ее осью симметрии, на которой сосредоточены источники или стоки с постоянной линейной плотностью F. Случай F >  0 соответствует ист<шпикам. а случай F <  0 — стокам. Теорема существования решения соответствующей задачи протекания доказана при выполнении

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ одностороннего неравенства F < 2nv. Оно накладывает ограничение на интенсивность источников, в то время как интенсивность стоков может быть любой.

Следующая гипотеза представляется вполне правдоподобной. Пусть течение имеет две плоскости симметрии, которые пересекают каждую связную компоненту границы области течения. Пусть входные данные задачи протекания удовлетворяют условиям, указанным в формулировке Леммы 2. Тогда задача протекания имеет, по крайней мере, одно обобщенное решение.

Автор вырамсает признательность К. Пилецкасу и М.В. Коробкову за внимание к работе и полезные обсуэюдения.