Трехмерное моделирование в исследованиях глиняных сосудов саргатской культуры раннего железного века барабы: фиксация метрических характеристик

Сосуды из глины являются важнейшим источником для интерпретации культурных процессов, происходивших с периода неолита вплоть до этнографического времени [Бобринский, 1978; Глушков, 1986; Дьякова, 1984; Жущиховская, 2004; Илюшина, 2016; Краева, 2017; Мочалов, 2008]. В рамках спецкурса «Керамика как археологический источник» при подготовке студентов по специальности «Археология» важное место занимает тема «Формы керамических сосудов». Несмотря на обширную литературу по данному вопросу (подбор литературы см.: [Формы глиняных сосудов…, 2018]), большинство предложенных подходов основано на соотношении параметров сосудов. Исследования, в которых анализируются метрические характеристики этой категории артефактов, обычно базируются на мануальных измерениях линейкой и / или штангенциркулем.

Такие способы фиксации метрических характеристик не приводят к получению постоянных значений даже при работе с визуально простыми орудиями [Селецкий и др., 2020]. Одним из решений данной проблемы является применение методов трехмерного моделирова- ния, поскольку компьютерные измерения следуют одному повторяющемуся алгоритму, из-за чего полученные данные не разнятся [Karasik, Smilansky, 2008].

Цель настоящего исследования заключается в апробации и выявлении основных возможностей использования методов 3D-моделирования при изучении керамических сосудов раннего железного века.

Материалы и методы

Источником для написания данной работы послужила коллекция керамических сосудов саргатской культуры раннего железного века кургана № 51 могильника Усть-Тартасские курганы [Мыльникова и др., 2022]. Из насыпи и 22-х погребений выявлено 32 сосуда – целые и фрагментированные [Там же]. Артефакты были подвергнуты трехмерному моделированию посредством применения сканера структурированного подсвета «RangeVision Spectrum» при использовании следующего программного обеспечения:  «RangeVision ScanCentre»,

«Geomagic WRAP», «Geomagic Design X», «Keyshot 10» (все – trial version) [Чистяков и др., 2021].

Для реализации экспериментов по замерам метрических характеристик компьютерным и мануальным способами были отобраны три сосуда.

Сосуд 1 (рис. 1) – целый, круглодонный, закрытый (диаметр венчика меньше максимально диаметра тулова), горшковидный, с очень низкой горловиной, сформированной путем отгиба наружу приостренного венчика.

Сосуд 2 (рис. 2) – целый, плоскодонный, закрытый, горшковидный, с высокой горловиной, отогнутой наружу, округлым в плане венчиком.

Сосуд 3 (рис. 3) – фрагментирован, круглодонный, закрытый, горшковидный, с высокой горловиной, отогнутой наружу, округлым в плане венчиком.

В эксперимент приглашены 12 исследователей ИАЭТ СО РАН: семь из них занимаются проблемами археологии палеометалла, пять – каменного века. Экспериментальная база по технологическим вопросам гончарства в России разработана. «Более сложными в плане обоснования и представления результатов являются эксперименты, ориентированные на исследование поведенческих стереотипов» [Собольникова, 2008]. Но именно такие эксперименты актуальны сегодня. В связи с тем, что количество участников эксперимента является не репрезентативным (менее 30), настоящее исследование носит предварительный характер.

Рис. 1. Визуализация 3D-модели круглодонного сосуда (угол поворота 90ᶿ)

Fig. 1. Visualization of a 3D-model of a round-bottomed vessel (rotation angle 90ᶿ)

Респонденты отбирались случайным образом. Но учитывался их исследовательский опыт работы с керамическими изделиями. Пятеро из них прослушали курс «Керамика как археологический источник» в НГУ и имели опыт анализа этой категории археологических артефактов только в полевых условиях. Остальные (семеро) – опытные исследователи, которые активно участвуют в раскопочных работах памятников эпох неолита, бронзового и железного веков, средневековья и активно публикуются в ведущих российских и международных журналах по тематике представленных выше комплексов.

Рис. 2. Визуализация 3D-модели плоскодонного сосуда

Fig. 2. Visualization of a 3D-model of a flat-bottomed vessel

Рис. 3. Визуализация 3D-модели фрагмента круглодонного сосуда

Fig. 3. Visualization of a 3D-model of a fragment of a round-bottomed vessel

Участникам эксперимента были предложены инструменты: линейки, треугольники, штангенциркули. Поставлена задача (без дополнительных пояснений): провести измерение диаметра венчика и высоты сосудов.

Методологическую базу этого исследования составили примеры Л. Гросман [Grosman et al., 2008]. Частично такой способ анализа археологических артефактов был апробирован при изучении коллекций каменных ударно-абразивных орудий [Белоусова и др., 2023; Се-лецкий и др., 2020].

В качестве точного показателя метрических характеристик археологических артефактов выбраны компьютерные замеры диаметров венчиков и высоты сосудов. Поскольку программные данные являются постоянными, их значение не изменяется в зависимости от количества фиксаций.

Для этого в программе «Geomagic Design X» были выделены модели сосудов, а расчет нужных параметров происходил путем выявления компьютером наборов точек, располагающихся параллельно и / или субпараллельно и создающих наибольшие плоскости на поверхности артефактов. Далее рассчитывались метрические характеристики этих плоскостей, откуда мы и получили диаметр венчика и высоту сосуда в миллиметрах.

«Компьютерно-мануальные» замеры метрических характеристик исследуемых объектов производились в программе «Geomagic Design X» путем установки двух точек на противоположных краях венчика и от венчика до дна сосуда, между которыми измерялась дистанция. Визуализация полученных данных происходила в программах «Keyshot 10» (проекции сосудов) и «Statistica 12» (графическое отображение метрических параметров).

Мануальные же измерения подверглись арифметическому анализу в совокупности с мерой описательной статистики. Для фиксации расхождения показателей приведены его диапазон и среднее арифметическое.

В рамках статистического анализа экспериментальных выборок были применены следующие методы: дисперсионный тест ANOVA и t-критерий Стьюдента. Подсчеты осуществлялись в программе PAST [Hammer et al., 2001].

Результаты исследования

В рамках исследования проведена серия экспериментов, касающихся сравнения компьютерных и мануальных замеров метрических характеристик керамики.

Первая часть эксперимента состояла в измерении метрических характеристик круглодонного сосуда. Диаметр его венчика, согласно компьютерным данным, составляет 128,27 мм, высота – 119,26 мм (см. рис. 1).

Максимальные и минимальные расхождения в показаниях респондентов при фиксации диаметра венчика составляют 1,97 и 0,27 мм, высоты – 13,26 и 1,26 мм соответственно. Среднее арифметическое измерений респондентов составляет: диаметр венчика – 127,38 мм, высота – 114,09 мм. Респонденты, участвующие в эксперименте, кроме одного замера, указали меньшие метрические характеристики относительно программных.

Если рассматривать результаты группы специалистов в этой области и исследователей археологических объектов каменного века, то здесь получены следующие результаты. У первой группы погрешность при измерении диаметра венчика составила 0,27–1,27 мм, у второй – 0,27–2,27 мм. При фиксации высоты сосуда неточность у первой группы составила 3,26–13,26 мм, второй – 1,26–6,96 мм.

Суммируя изложенные данные, отметим, что первая группа была более точна в максимальных значениях при измерении диаметра венчика (разница 1 мм – максимальное значение), вторая группа – при измерении высоты сосуда (разница 2 мм – минимальное значение, 6,3 мм – максимальное значение).

Следующий этап эксперимента включал замеры параметров плоскодонного сосуда (максимальный диаметр венчика – 75,23 мм, высота сосуда – 130,72 мм; см. рис. 2). Максимальные и минимальные расхождения при фиксации диаметра венчика составляют 3,01 и 0,21 мм, высоты – 13,5 и 2,6 мм соответственно. Согласно приведенным выше данным, среднее арифметическое мануальных замеров диаметра венчика – 82,67 мм, высоты сосуда – 127,57 мм.

Респонденты указали меньшие метрические характеристики при фиксации высоты сосуда, однако при измерении диаметра венчика лишь три показателя были меньше компьютерного.

Если рассматривать неточности измерений диаметра венчика и высоты сосуда по группам, то первая получила следующие параметры: 0,21–3,01 и 4,34–19,94 мм; вторая – 0,21– 3,01 и 3,84–11,34 мм соответственно. При анализе диаметра венчика диапазон неточностей совпадает у обеих групп. Интересны данные о расхождениях замеров высоты сосуда: специалисты по каменным индустриям оказались точнее как по минимальным, так и по максимальным значениям (разница 0,5 и 8,6 мм соответственно).

Для выявления возможности исследования мануальных метрических характеристик представленной категории артефактов с помощью методов статистики был проведен дополнительный эксперимент – сравнение параметров «компьютерно-мануальных» и мануальных измерений диаметра венчика и высоты рассматриваемого сосуда.

Поскольку все выборки продемонстрировали нормальность распределения по тесту Шапиро – Уилка, то для сравнения трех выборок использовался дисперсионный тест ANOVA. При сравнении измерений венчика сосуда 2, было получено значение теста F = 2,56, при p = 0,1, что означает отсутствие статистических различий между тремя группами «машинномануальных» и мануальных измерений (рис. 4, 1 ).

При сравнении длины между тремя выборками с использованием теста ANOVA получены значения теста F = 9,94, при p = 0,001 (рис. 4, 2 ). Этот результат свидетельствует о статистически значимой разнице между выборками. При этом попарное сравнение с использованием t -критерия Стьюдента показало статистическую разницу между мануальными и «компьютерно-мануальными» измерениями ( t = 4,5, p = 0,0013 c группой 1; t = 4,2, p = 0,0013 с группой 2), при отсутствии разницы между двумя группами мануальных измерений ( t = 0,99, p = 0,34). Это может означать, что мануальные отклонения увеличиваются при измерении артефактов со сложной формой. При этом обе группы респондентов не отличаются по качеству измерений друг от друга.

А    В    С

Рис. 4. График выборок «компьютерно-мануальных» и мануальных измерений плоскодонного сосуда:

• 1    – диаметр по венчику; 2 – высота сосуда (A – выборка «компьютерно-мануальных» измерений, B – выборка измерений первой группы исследователей; C – выборка измерений второй группы исследователей)

• Fig. 4. Jitter plots showing comparisonof “computer-manual”

and manual measurements of a flat-bottomed vessel:

• 1    – the diameter of the corolla; 2 – vessel height (A – sample of “computer-manual” measurements, B – sample of measurements by Stone age researchers; C – sample of measurements by Iron/Bronze age researchers)

В рамках третьего этапа эксперимента проведен анализ метрических характеристик фрагмента круглодонного сосуда (диаметр венчика – 81,79 мм, высота сосуда – 138,34 мм; см. рис. 3). Максимальная и минимальная погрешности при замерах максимального диаметра венчика составляют 3,93 и 0,23 мм, высоты – 13,52 и 2,7 мм соответственно. Респонденты указывали меньшие величины при замерах высоты сосуда и расходились «в обе стороны», когда измеряли диаметр венчика. Среднее арифметическое мануальных замеров диаметра венчика составляет 73,19 мм, высоты сосуда – 124,6 мм.

При исследовании метрических характеристик диаметра венчика и высоты сосуда диапазон неточностей первой группы составил 0,23–3,83 и 3,42–13,52 мм, второй – 0,43–3,93

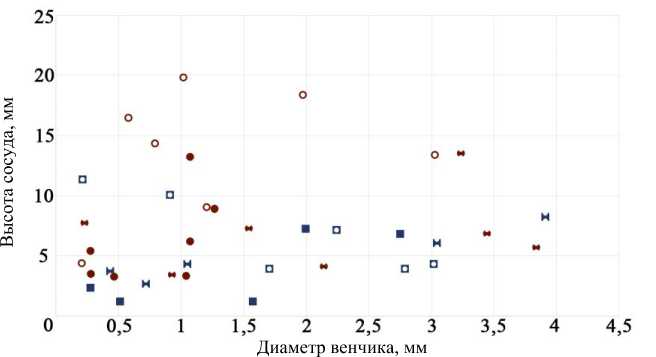
■ – замеры круглодонного сосуда, выполненные респондентами 2-й группы □ – замеры плоскодонного сосуда, выполненные респондентами 2-й группы н – замеры фрагмента круглодонного сосуда, выполненные респондентами 2-й группы • – замеры круглодонного сосуда, выполненные респондентами 1-й группы о – замеры плоскодонного сосуда, выполненные респондентами 1-й группы м – замеры фрагмента круглодонного сосуда, выполненные респондентами 1-й группы

Рис. 5. Расхождение мануальных измерений с компьютерными (0 мм) при измерении диаметров венчиков и высоты исследуемых сосудов Fig. 5. Discrepancy between manual measurements and computer ones (0 mm) when measuring the diameters of the corollas and the height of the vessels under study и 2,62–8,22 мм соответственно (рис. 5). Первая группа оказалась точнее при измерении диаметра венчика как в минимальном, так и в максимальном значении (разница 0,2 и 0,1 мм соответственно), вторая группа значительно превзошла их показатели при фиксации метрических параметров высоты сосуда (разница 0,8 мм – минимальное значение, разница 7,3 мм – максимальное значение).

Обсуждение и выводы

По результатам проведенного исследования были апробированы методы изучения трехмерных моделей археологических артефактов, проведен эксперимент, заключающийся в сравнении мануальных замеров респондентов между собой и с программным параметром.

Наименьшие расхождения респондентов наблюдались в измерениях диаметра венчиков сосудов вне зависимости от их формы или целостности. В среднем до программной характеристики обеим группам не хватало от 0,1 до 3 мм. Что касается замеров высоты сосудов, ближе к компьютерному значению респондентам удалось исследовать плоскодонный сосуд (расхождение 3,15 мм по среднему арифметическому), большее расхождение отмечено с круглодонным изделием (5,17 мм) и фрагментом артефакта (13,74 мм). Это может быть связано с тем, что диаметр венчика фиксируется в рамках прямой плоскости. При замере высоты сосуда линейки, штангенциркули и пр. инструменты пересекаются с вогнутым и / или выгнутым рельефом венчика и туловом артефакта, что и создает такие расхождения в этом параметре у исследователей.

При анализе расхождений в измерении метрических параметров у двух групп археологов, разделенных по специализации, было выявлено, что параметры диаметра венчика не сильно расходились (0,1–1 мм). С другой стороны, при анализе значений высоты сосудов была выявлена следующая тенденция. Сотрудники отдела археологии каменного века ИАЭТ СО РАН более точно зафиксировали этот параметр, но разница при минимальных расхождениях зачастую составляла менее 1 мм, тогда как максимальные значения расходились вплоть до 7 мм.

По результатам предварительного статистического анализа были выявлены следующие тенденции. Расхождения групп исследователей по метрическим измерениям сосудов отсутствуют. В сравнении с «компьютерно-мануальными» параметрами для реализации статистического анализа является допустимым изучение мануальных значений, определенных в рамках одной плоскости (диаметр венчика), когда как на поверхностях со сложным рельефом (высота сосуда) ученым следует обратиться к машинным данным или применять специализированные инструменты (например, профилемеры – копировальные шаблоны).

Согласно представленным выше предварительным результатам, можно констатировать, что точность мануальных измерений параметров сосудов не зависит от квалификации исследователя. «Простые» замеры (на плоскости без выраженного рельефа) фактически не отличаются от машинных и могут использоваться для проведения арифметического и статистического анализа. В случае с получением метрических характеристик морфологически «сложных» поверхностей мы зафиксировали значительную разницу по сравнению с машинными измерениями, поэтому лучше обратиться к компьютерным измерениям трехмерных моделей.

Изучение метрических характеристик керамических изделий является перспективным для выявления культурной и / или хозяйственно-бытовой специфики древних сосудов. Однако, чтобы проводить доказательные арифметические и статистические исследования, необходимо апеллировать к точным параметрам артефактов. Это становится достижимым с помощью применения методов трехмерного моделирования.