Трехмерные адвективные течения в горизонтальном цилиндре квадратного сечения с теплоизолированными боковыми границами

ампула медленно выводится из горячей зоны печи в более холодную. Вследствие охлаждения на заостренном дне ампулы образуется кристалл-зародыш, из которого при дальнейшем движении тигля формируется монокристалл.

В литературе имеется большое количество работ, посвященных изучению одно- и двумерных адвективных течений в плоском горизонтальном слое и в вытянутой по горизонтали прямоугольной области при различных тепловых условиях на границах. Так, устойчивость адвективного течения в плоском горизонтальном слое с твердыми границами исследовалась численно методом Галеркина в работах [1, 2] для случая идеально теплопроводных границ (при плоских [1] и пространственных [2] возмущениях; см. также монографию [3]) и в работе [4] для случая теплоизолированных границ.

В [1] показано, что стационарное плоскопараллельное течение может стать неустойчивым относительно двух плоских мод возмущений. При малых числах Прандтля неустойчивость имеет гидродинамическую природу и связана с развитием вихрей на границе встречных потоков. В области умеренных и больших чисел Прандтля за неустойчивость отвечают плоские релеевские моды, обусловленные возникающей температурной стратификацией.

В работе [2] выявлено, что в широкой области значений числа Прандтля (Pr >  0,14) кризис течения вызывается пространственными спиральными возмущениями, которые имеют вид валов с осями, параллельными направлению основного течения, и представляют большую опасность, чем плоские возмущения релеевской природы.

Позже установлено, что в сравнительно узкой области чисел Прандтля от 0,14 до 0,45 наиболее опасна спиральная колебательная мода неустойчивости, по своей физической природе связанная с возбуждением (за счет энергии основного потока) внутренних волн в слое устойчивой стратификации, а при Pr >  0,45 неустойчивость обусловлена развитием в неустойчиво стратифицированных слоях жидкости, прилегающих к верхней и нижней границам слоя, спиральных монотонных возмущений, имеющих релеевскую природу [3].

В работе [4] рассмотрен случай адиабатических границ слоя. Обнаружено, что в области малых чисел Прандтля нижние уровни неустойчивости соответствуют плоской монотонной гидродинамической моде (наиболее опасной при Pr <  0,033) и спиральной колебательной моде (наиболее опасной в диапазоне 0,033 <  Pr <  0,2), а при Pr >  0,2 за развитие неустойчивости отвечают монотонные спиральные возмущения.

Также имеется ряд работ, в которых исследовались трехмерные стационарные адвективные течения в горизонтальных каналах кругового и прямоугольного поперечного сечения. В работах [5, 6] численно (методом конечных разностей) получены решения трехмерных уравнений естественной конвекции в горизонтальном канале кругового сечения при наличии продольного градиента температуры. Стенки канала предполагались идеально теплопроводными. Изучены характеристики перехода от режима течения в ядре к режиму течения в пограничном слое.

В работе [7] рассматривались адвективные течения в длинном горизонтальном канале прямоугольного сечения, на торцах которого поддерживались различные температуры, а другие грани были теплоизолированы. Путем численного решения трехмерных уравнений Навье–Стокса в приближении Буссинеска, записанных для замкнутого канала, проведен анализ устойчивости основного течения, исследована пространственная структура конвекции при изменении числа Грасгофа и размеров (длины и ширины) области. Все расчеты выполнены для случая Pr = 0 .

В работах [8, 9] исследована устойчивость стационарных адвективных течений в длинном горизонтальном канале прямоугольного сечения с идеально теплопроводными границами при нулевом и отличных от нуля значениях числа Прандтля и наличии однородного продольного градиента температуры. В [8] обнаружено, что плоскопараллельное стационарное решение возможно лишь при нулевом значении числа

Прандтля; при отличных от нуля значениях таких решений не существует. В поперечном сечении канала наблюдались четыре вихря, так что траектории частиц представляли собой спирали с осями, параллельными образующей канала. Рассматривалось влияние на устойчивость трехмерных возмущений, периодических вдоль оси канала, при нулевом значении числа Прандтля. В [9] для отличных от нуля значений числа Прандтля был обнаружен эффект резкого повышения устойчивости основного течения по отношению к гидродинамическим возмущениям, характерный для малых значений числа Прандтля.

Та же задача, что и в [9], в работе [10] изучена для случая теплоизолированных боковых границ. Получены нейтральные кривые и карты устойчивости относительно плоских монотонных гидродинамических и спиральных колебательных возмущений для различных наборов параметров (числа Прандтля, ширины канала). Найдено, что имеет место, как и в случае идеально теплопроводных границ канала, резкая стабилизация течения при малых числах Прандтля.

В работе [11] обсуждалось влияние акустического воздействия на трехмерные адвективные течения в горизонтальном канале квадратного сечения и конечной длины в случае идеально теплопроводных боковых границ. Анализировались перестройка структуры течения с ростом числа Грасгофа, влияние длины канала, числа Прандтля и параметров акустического воздействия на структуру течения. Построены бифуркационные диаграммы.

В настоящей работе численно исследуются трехмерные адвективные течения в горизонтальном цилиндрическом канале квадратного поперечного сечения и конечной длины в случае теплоизолированных границ канала. Эта задача до сих пор не рассматривалась, хотя с точки зрения приложений к процессам выращивания кристаллов методом Бриджмена, более важным является случай именно теплоизолированных границ. Статьи, содержащие экспериментальные результаты, с которыми можно было бы провести сравнение, в литературе отсутствуют.

• 2.    Постановка задачи трехмерного адвективного теченияв горизонтальном канале квадратного сечения и конечной длины

Задача формулируется с учетом постоянного однородного градиента температуры, параллельного продольной оси канала. Вводится прямоугольная декартова система координат так, что ее начало лежит на оси канала в середине длины l , ось х совпадает с осью канала, а оси y (горизонтальная) и z (вертикальная) располагаются в плоскости его поперечного сечения (Рис. 1).

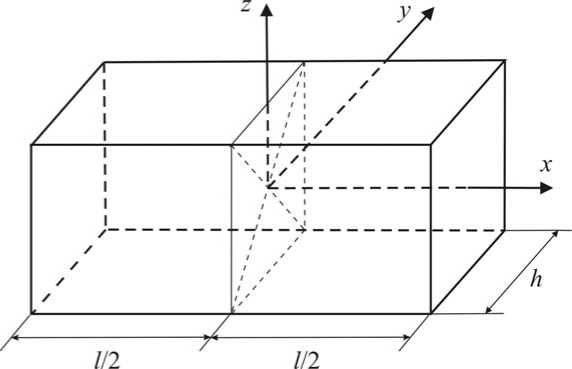
Рис. 1. Геометрия задачи

Считается, что границы канала, ориентированные вдоль его оси, твердые и на них выполняется условие прилипания. На границах, перпендикулярных оси канала (торцах), задаются постоянные разные температуры T ( - 1 /2) = T 1 , T ( 1 /2) = T ₂ ( T 1 < T ₂); остальные границы полагаются теплоизолированными.

Для описания течения используются записанные в безразмерной форме уравнения свободной тепловой конвекции в приближении Буссинеска:

— + Gr (vV) v = -Vp + Av + Tj,(1)

ar       , .1

— + Gr (vV) T = — AT ,(2)

dt      v ’Pr div V = 0.(3)

Здесь v = ( U , V , W ) — скорость, p — конвективная добавка к гидростатическому давлению, T — температура жидкости, j = (0, 0,1) — единичный вектор в направлении оси z . В качестве единиц измерения длины, времени, скорости, давления и температуры выбираются соответственно: h ; h² /v ; g в Ah ³ /v; g в Ah ²; Ah ( v — коэффициент кинематической вязкости, g — ускорение силы тяжести, в — коэффициент теплового расширения, A = ( T ₂ - T 1 )/ / — продольный градиент температуры). Уравнения содержат два безразмерных параметра: число Грасгофа Gr = g в Ah ⁴/v ² и число Прандтля Pr = v/x ( x — коэффициент температуропроводности). Еще одним безразмерным параметром задачи является отношение длины канала к длине стороны его поперечного сечения: L = 1/h .

• 3.    Метод решения

Задача решалась в терминах «скорость–давление» численно с помощью коммерческого пакета прикладных программ FLUENT 6.3.26, входящего в состав программного комплекса ANSYS и предназначенного для моделирования течений жидкости и газа. Присутствие в пакете большого числа физических моделей позволяет исследовать ламинарные и турбулентные течения, различные режимы теплопереноса, химические реакции, многофазные потоки и другие явления на основе гибких сеток, адаптируемых к отыскиваемому решению. Благодаря возможности использования многосеточных методов с улучшенной сходимостью пакет FLUENT способен обеспечить оптимальную эффективность и точность решения для широкого диапазона моделируемых скоростных режимов.

Минимальная оперативная память компьютера, необходимая для работы в данном пакете, составляет 512 Мб. Пакет поддерживает 32- и 64-разрядные версии ОС Windows, а также ОС Linux. К недостаткам пакета следует отнести, прежде всего, высокую стоимость лицензионной версии, а также ограничения, заложенные в сами физические модели, доступные в пакете, и ограничения возможности модификации этих моделей.

Использовалась нестационарная постановка; проводилось наблюдение за выходом на стационарные значения ряда характеристик течения. Шаг по времени в расчетах равнялся т« 0,0033. Для дискретизации по времени использовалась неявная схема второго порядка, для дискретизации по пространству — схема третьего порядка MUSCL (Monotone Upstream-Centered Scheme for Conservation Laws), представляющая собой объединение схемы центральных разностей и схемы второго порядка «назад».

Выбранные схемы являются наиболее точными из возможных вычислительных схем, доступных при использовании пакета FLUENT.

Схему MUSCL можно пояснить на примере одномерного дифференциального уравнения ut + Fx (u) = 0 .

Уравнение записывается в дискретной форме:

du 1

dt Axi

F i - F i l+— I —

= 0.

Здесь

F i = | J F ( u^R i ) + F ( u^L i ) i ±—   /         i —        i—

2       Ц_       2            2

где a ] (t) = max p i ±1 2_

a

± 2

R

5 F ( U i ( t )) ) J d F ( U ± i ( t )) d u    / , (     5 u

,

p — спектральный радиус величины

dF ( u ( t ))

. Подробное описание данной схемы приводится в работе [12].

du

Расчеты проводились на равномерной сетке с кубическими ячейками. Величина шага сетки выбиралась на основании серии тестов, которые заключались в решении той же задачи с использованием сеток разного размера и анализе сходимости вычислений при измельчении шага сетки. Результаты, полученные на сетках с шагом 130, 140 и 1/50 при Pr = 0,01, L = 6, Gr = 85000, показали, что при сопоставлении компонент скорости, полученных на сетках с шагом 130 и 140, отличие составляет 3%, а с шагом 140 и 150 — 0,7%. На основании этого был сделан вывод, что выбор сетки с шагом 140 позволяет получить оптимальное соотношение между точностью искомых численных результатов и временем решения задачи. Таким образом, в основных вычислениях использовалась пространственная сетка размерностью ( 40 L х 40 х 40 ) . Параметр релаксации для импульса и давления принимался равным 0,75, число Куранта — 200.

• 4.    Численные результаты

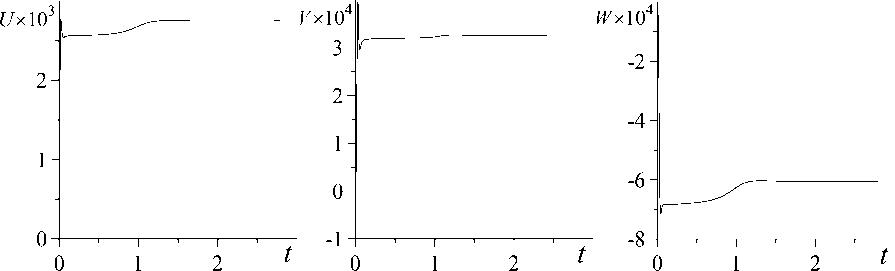
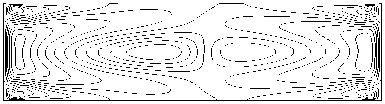
На рисунке 2 приведены временная эволюция компонент скорости U , V , W в точке полости с координатами ( L /4; 0,25; 0,25 ) и изолинии продольной компоненты скорости в трех сечениях канала для случая L = 4, Pr = 0,01 (данное число Прандтля характерно для жидких металлов).

При малых числах Грасгофа течение имеет одновихревую структуру: в нижней части области жидкость движется в направлении, совпадающем с направлением приложенного градиента температуры, в верхней части — в противоположном направлении. Течение обладает двумя видами симметрии (Рис. 2, г ): зеркальной симметрией по отношению к смене знака y (продольная скорость есть четная функция y ) и инверсионной симметрией в плоскости ( x, z ) (при инверсии продольная скорость

U x10³

V X10⁴.

W X10⁴

а

6 t

-1

6 t

-2

-4

-6

-8

t

б

W x10⁴

-2

-4

-6

t

x = 0

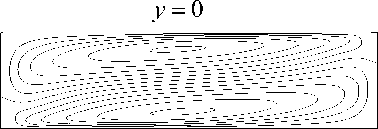
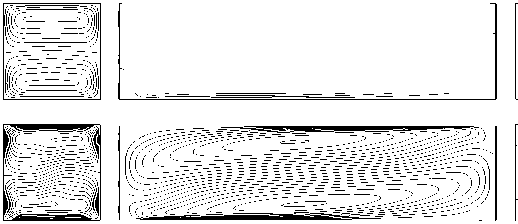
Рис. 2. Временная эволюция компонент скорости U , V , W ( а, б, в ) в точке с координатами

( L /4; 0 , 25; 0 , 25 ) при Pr = 0 , 01, L = 4 и числах Грасгофа Gr : 40000 ( а ), 66000 ( б), 146000 ( в );

изолинии продольной компоненты скорости ( г, д ) в сечениях x = 0 , у = 0 , z = 0, отвечающие случаям ( а , б ) соответственно

в

меняет знак) . Данному течению соответствует решение типа I. Характеристики этого течения после переходного процесса выходят на стационарные значения (Рис. 2, а – в ).

При числах Грасгофа, превышающих значение Gr * 66000, после переходного процесса устанавливается стационарное течение, обладающее симметрией, являющейся суперпозицией двух указанных выше видов симметрии, но не имеющее каждой из этих видов симметрии по отдельности (Рис. 2, д). Этому течению соответствует решение типа II. Дальнейшее увеличение числа Грасгофа приводит к тому, что при Gr * 146000 возникают стационарные колебания, но симметрия течения не изменяется (Рис. 2, в).

Для выяснения природы осцилляций нестационарного решения были проведены проверочные расчеты при различных значениях параметров вычислительной схемы: шага по времени, размера сетки, порядков аппроксимации по времени и по пространству, параметра релаксации для импульса и давления, числа Куранта. Расчеты показали, что наличие колебаний и их характеристики не зависят от изменения параметров схемы. На этом основании был сделан вывод, что пульсации нестационарного решения не являются осцилляциями схемных ошибок, а отражают реальный физический процесс.

Рисунок 3 содержит зависимость продольной компоненты скорости течения в точке области с координатами ( L] 4; 0,25; 0,25 ) от числа Грасгофа для L = 4, Pr = 0,01. Видно, что при Gr _S| * 66000 (в точке S 1 ) зависимости U (Gr) претерпевают излом. Излом обусловлен тем, что при таком числе Грасгофа изображенное на рисунке 2, а , г решение типа I становится неустойчивым и в результате вилочной бифуркации возникает новое решение с другим видом симметрии (см. Рис. 2, б , д ). При дальнейшем увеличении числа Грасгофа решение типа II, в свою очередь, теряет устойчивость, и в точке O ₂ (Gr ₀₂ * 146000) в результате бифуркации Хопфа происходит переход к колебательному режиму течения (см. Рис. 2, в ). На рисунке 3 участок правее точки O ₂ (пунктирная линия) изображает средние значения компоненты скорости U . Бифуркация Хопфа не сопровождается сменой вида симметрии.

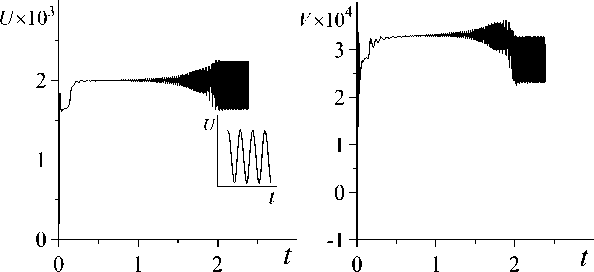
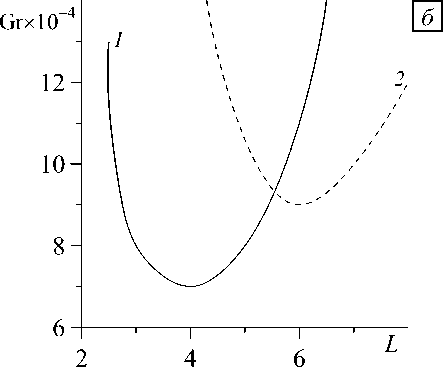
На рисунке 4 показаны зависимости чисел Грасгофа, при которых наблюдаются вилочная бифуркация (кривая 1 ) и бифуркация Хопфа (кривая 2 ), от относительной длины канала L в случае Pr = 0,01. Видно, что обе кривые имеют немонотонный характер. Критическое число Грасгофа, соответствующее вилочной бифуркации, минимально при L * 4, а число Грасгофа, при котором возникают колебания, минимально при L * 6 . Для длин канала, лежащих в интервале 4 <  L <  6,5, могут иметь место обе бифуркации: при 4 <  L <  5,5 сначала наблюдается вилочная бифуркация, а затем — бифуркация Хопфа; при 5,5 <  L <  6,5 порядок следования бифуркаций обратный (см. рисунок 5, а , б , где для двух значений числа Грасгофа — ниже и выше точки бифуркации — приведены характеристики течения в точке области

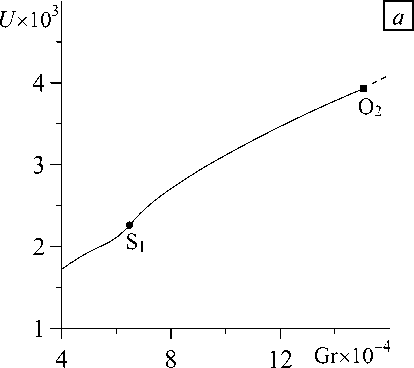
Рис. 3. Бифуркационная диаграмма             Рис. 4. Влияние относительной длины канала L в случае Pr = 0,01 и L = 4              на числа Грасгофа, при которых происходит смена вида симметрии течения (кривая 1) и возникает колебательный режим (кривая 2); Pr = 0,01

U x10³

V x10⁴

W x10⁴

а

t

-1

t

-1

-2

-3

t

U x10³

U x10³

V x10⁴

t

-1

V x10⁴

x = 0

y = 0

t -1 ₀

Рис. 5. Временная эволюция компонент скорости U , V , W ( а, б , в ) в точке с координатами

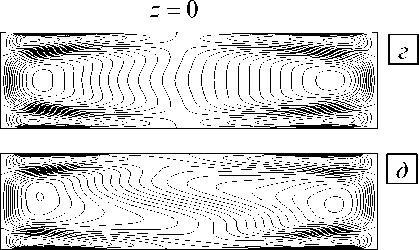
( L) 4; 0 , 25; 0 , 25 ) при Pr = 0 , 01, L = 6 ( а, б), L = 8 ( в ) и числах Грасгофа Gr 90000 ( а ), 110000 ( б),

120000 ( в ); изолинии продольной компоненты скорости ( г ) в сечениях x = 0 , у = 0 , z = 0 в момент времени t = 1 , 2 , отвечающие случаю ( в )

W x10⁴

-1

-2

-3

б

t

-4

W x10⁴

-1

-2

-3

t

в

t

t

z = 0

г

с координатами ( L /4; 0,25; 0,25 ) в случае Pr = 0,01, L = 6). Длинам, лежащим за пределами интервала (для L <  4 и L >  6,5) отвечает лишь одна из бифуркаций (см. Рис. 5, в , г ; на рисунке изображены характеристики течения в рассматриваемой точке области и изолинии продольной компоненты скорости при L = 8).

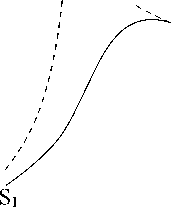
На рисунке 6 представлены зависимости чисел Грасгофа, при которых наблюдаются бифуркации, от числа Прандтля в случае L = 4. Как видно, при малых значениях числа Прандтля сначала имеет место вилочная бифуркация, а затем, с повышением числа Грасгофа, — бифуркация Хопфа. При Pr > 0,02 бифуркация, приводящая к нарушению симметрии, отсутствует, отмечается лишь бифуркация Хопфа, не нарушающая симметрию.

Для иллюстрации возникновения бифуркации Хопфа на рисунке 7 приведены характеристики течения в точке области с координатами ( L) 4; 0,25; 0,25 ) для L = 4 при малом значении числа Pr = 0,025 и двух значениях числа Грасгофа, лежащих ниже и выше точки бифуркации.

Gr x10^-4          O 2¹

O 1

0          1          2     Pr x10²

Рис. 6. Зависимость числа Грасгофа, при котором наблюдается вилочная бифуркации (кривая S ₁ ), и чисел Грасгофа, при которых имеет место бифуркация Хопфа (кривые O ₁ и O ₂ ), от числа Прандтля при L = 4

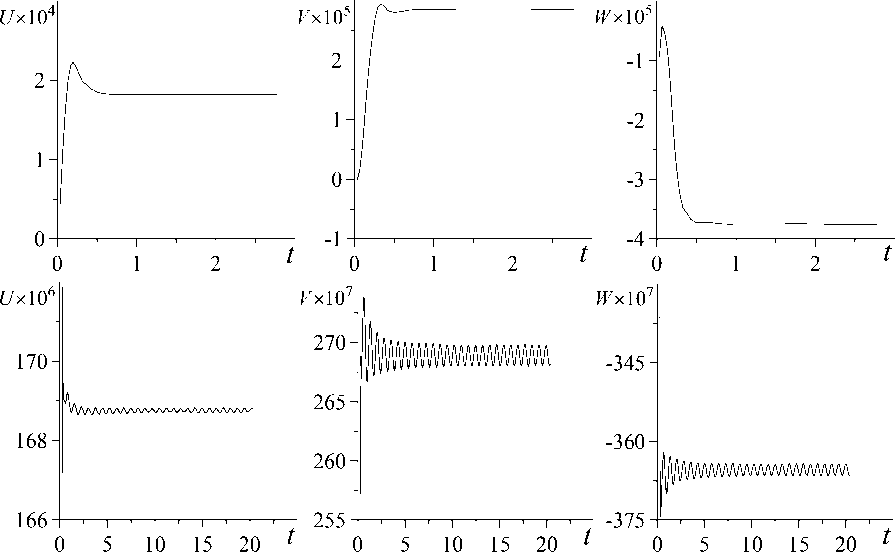
Рис. 7. Временная эволюция компонент скорости U , V , W в точке с координатами ( L /4; 0,25; 0,25 ) при Pr = 0,025 , L = 4 и значениях числа Грасгофа Gr : 90000 ( а ); 100000 ( б)

• 5.    Заключение

Численно исследовано трехмерное адвективное течение в горизонтальном канале квадратного сечения с теплоизолированными боковыми границами. Показано, что на структуру течения существенно влияют число Грасгофа, длина канала и число Прандтля; при различных значениях этих параметров течение может по-разному вести себя во времени и обладать различными видами симметрии. В результате расчетов построены бифуркационные диаграммы и в зависимости от числа Прандтля и длины канала установлены критические значения чисел Грасгофа, при которых происходит смена режима течения. Построены графики, демонстрирующие различные варианты перехода к колебательным режимам течений (бифуркация Хопфа): либо с предварительным нарушением симметрии течения (вилочная бифуркация), либо без смены вида симметрии. Найдена область параметров, в которой имеет место лишь вилочная бифуркация, а колебательные режимы течения не возникают.