Трехслойная стеклопластиковая оболочка при термомеханическом воздействии

Объем использования конструкций из полимерных композиционных материалов в строительстве промышленных объектов с каждым годом растет. Перспективным направлением использования являются крупногабаритные коррозионностойкие конструкции [1], [2]. Оценка рациональной области применения полимерных композитов в газоходах промышленных и вентиляционных труб представлена в работах [3]. Особенности инженерных расчетов подобных конструкций описаны в [4], [5]

Применение стеклопластиковых оболочек, в частности в газоходах металлургических предприятий [6], обуславливается высокой коррозионной стойкостью, по сравнению с конструкциями из традиционных материалов. При этом многие промышленные предприятия заинтересованы в применении композитных газоходов при температурах не менее 180-200°С [7].

В работах [8]–[10] описано влияние длительного воздействия повышенных температур на модуль упругости и температуру стеклования ряда термореактивных связующих, а также на термомеханические свойства эпоксидных стеклопластиков, выполненных на основе этих связующих. Показано, что происходит увеличение модуля упругости полимеров при длительной выдержке образцов при повышенных температурах, а также увеличение температуры их стеклования. Также процесс старения эпоксидного связующего и изменение его физикомеханических свойств исследованы в работе [11], в частности наблюдалось повышение модуля упругости в результате термического старения.

Предположение о возможности длительной эксплуатации газоходов из эпоксидных стеклопластиков (на основе смолы ЭД-20 или ее аналогов) при температурах до 200°С сделано в работах [9], [12], [13], несмотря на то, что эта температура выше температуры стеклования рассмотренных эпоксидных связующих. В данных исследованиях указывается что потеря массы Antipin, A.; Mishnev, M.

Three-layer fiberglass shell under thermomechanical action;

образцов при температурах до 200 °С носит затухающий характер и в конце концов останавливается, при этом стеклопластик сохраняет определенную жесткость.

В работе [7] показано, что после длительной выдержки (термического старения) при температурах выше начальной температуры стеклования модуль упругости возрастал на 60–90%, а при более низких не изменялся или же уменьшался незначительно, при этом прочность при изгибе незначительно снижалась. Обеспечение требуемой прочности и жесткости конструкции планируется обеспечить при помощи сэндвичевой структуры стенки оболочки, которая включает стеклопластиковые обшивки и средний слой заполнителя из теплоизоляционного материала. Помимо этого, повышение модуля упругости при термическом старении может в какой-то степени компенсировать потерю жесткости конструкции из-за снижения модуля упругости стеклопластика, подвергающегося воздействию повышенной температуры.

Анализ коррозионной стойкости полимерных составов для производства газоходов приведен в [14]. В работе [15] описано влияние армирующего волокна геополимера на характеристику ползучести. Влияние добавок древесной золы в композиты на термические напряжения в конструкциях трубопроводов представлено в [16]. В статьях [17], [18] показана возможность использования пластиковых отходов в производстве композитных газоходов и трубопроводов.

В статьях [19], [20] описывается способ производства трехслойных оболочек из полимерных композитных материалов методом намотки с подращиванием.

Исходя из анализа существующих исследований можно предположить, что есть возможность эксплуатировать газоходы на больших пролетах даже при повышенных температурах. Но для этого необходимо уточнить ряд характеристик сырьевых материалов, а также провести анализ работы конструкции в целом.

Целью настоящей работы является исследование прогибов трехслойной цилиндрической оболочки на реальной модели, и последующее сравнение полученных результатов с численным экспериментом.

Рассматривается двухопорная разрезная схема работы оболочки. Она отличается от наиболее популярной в практике: опирании оболочек на часто расположенные ложементы, при которой оболочка работает только в кольцевом направлении. В таком случае определяющими являются нагрузки, возникающие на этапе транспортировки и монтажа конструкции, при этом постоянные и временные эксплуатационные нагрузки воспринимаются стальной или железобетонной эстакадой. Примером реализации данной классической схемы могут служить конструкции газоходов, описанные в [21], в таких случаях не в полной мере используется собственная несущая способность и жесткость стеклопластиковых оболочек.

Для достижения поставленной цели необходимо решить следующие задачи:

• -    разработать программу проведения экспериментального определения деформированного состояния модели оболочки на термомеханическое воздействие;

• -    выполнить экспериментальные исследования деформированного состояния модели оболочки на термомеханическое воздействие;

• -    выполнить конечноэлементное моделирование эксперимента;

• -    провести сравнительный анализ полученных данных;

• 2    Materials and Methods

  2.1    Full-scale testing

Установка представляет собой: две металлические опоры, которые закрепляются в полу для обеспечения неподвижности в процессе эксперимента; набор стоек-держателей для датчиков перемещений часового типа; набор термопар для контроля температуры внутренней поверхности – вставляются в просверленные отверстия в оболочке с верхней ее стороны; термопушка с гофрой для подачи нагретого воздуха и разогрева внутренней поверхности трубы; подвесного ящика для нагружения конструкции. Датчики устанавливаются в характерных точках трубы: на верхней части опор, в центре пролета сверху, в центре пролета сбоку, в местах приложения нагрузки сверху и снизу. Ящик для нагружения закрепляется стропами с шагом 1 м в центре Antipin, A.; Mishnev, M.

Three-layer fiberglass shell under thermomechanical action;

конструкции. Нагружение осуществляется шагами ≈40 кг. Показания датчиков снимаются в установившемся положении после каждого шага нагружения. Процедура нагружения-разгрузки проводится для случая работы конструкции под температурой и без нее. Схема установки и ее реальный внешний вид показаны на Рисунке 1 и Рисунке 2 соответственно.

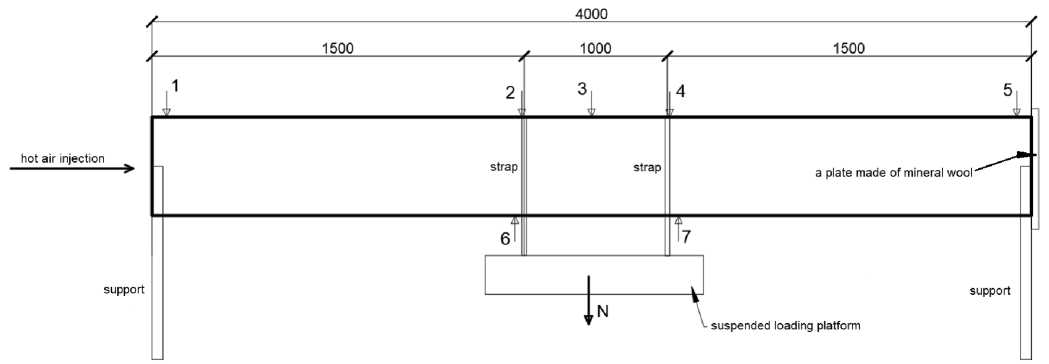
Рис. 1 – Схема эксперимента с расположением датчиков на образце (1 – датчик перемещений 1.1в.оп и термопара терм.1, 2 – датчик перемещений 2.1в.пр, 3 – датчик перемещений 3.1в.пр и термопара терм.2, 4 – датчик перемещений 2.2в.пр, 5 – датчик перемещений 1.2в.оп и термопара терм.3, 6 – датчик перемещений 4.1н.пр, 7 – датчик перемещений 4.2н.пр)

Fig. 1 – The scheme of the experiment with the location of sensors on the sample (1 – displacement sensor 1.1 v.op and thermocouple term.1, 2 – displacement sensor 2.1v.pr, 3 – displacement sensor 3.1v.pr and thermocouple term.2, 4 – displacement sensor 2.2v.pr, 5 – displacement sensor 1.2v.op and thermocouple term.3, 6 – displacement sensor 4.1n.pr., 7 – displacement sensor 4.2n.pr.)

Рис. 2 – Общий вид испытательной установки с образцом

Fig. 2 – General view of the test facility with a sample

Экспериментальный образец представляет из себя трехслойную оболочку. Внутренняя и наружная обшивки выполнены из стеклопластика на основе эпоксидного связующего горячего отверждения [14]; в качестве армирования выступает ткань конструкционная Т-23 по Российскому государственному стандарту ГОСТ 19907–83 «Ткани электроизоляционные из стеклянных крученых комплексных нитей» [29]. Средний слой выполнен из минераловатных плит

ТЕХНОНИКОЛЬ Техновент Стандарт (производитель: завод «ТЕХНОНИКОЛЬ Воскресенск», г. Воскресенск, Россия) с фактической плотностью 80 кг/м3.

Размеры оболочки:

• -    пролет 4 м

• -    диаметр наружный 380 мм

• -    толщины обшивок 2 мм

• -    толщина утеплителя 30 мм

Испытание разделено на две части. На первом этапе ненагретая оболочка нагружается за 6 шагов, на каждом шаге фиксируются показания датчиков. Далее следует разгрузка оболочки теми же шагами в обратном порядке, показания датчиков перемещений снимаются так же на каждом шаге. На втором этапе образец загружается единожды, после чего производится постепенный нагрев внутренней поверхности оболочки, отслеживаются показания термопар; при повышении температуры по показаниям термопар на определенных отметках температур снимаются показания датчиков перемещений.

Описанная ранее испытательная установка позволяет прогревать внутреннюю поверхность образца до 130оС. При дальнейшем нагнетании горячего воздуха тепло начинает распространяться на внешний слой, без повышения температуры внутренней обшивки. По достижении температуры в 130оС на внутренней обшивке, образец нагружается в два шага: сначала до 426.39 кг суммарной нагрузки, далее до 515.09 кг. Показания датчиков снимаются на каждом шаге догружения. Внешняя нагрузка на каждом этапе, а также показания термопар показаны в Таблице 1 (испытание без термического воздействия) и Таблице 2 (испытание с нагревом внутренней поверхности оболочки).

Таблица 1. Этапы нагружения образца без температуры

Table 1. Stages of sample loading without temperature

	Loading stage
	0	1	2	3	4	5	6
Load N, kg	0	85	174.4	260.44	345.39	426.39	515.09

Таблица 2. Этапы нагружения образца при термомеханическом воздействии

Table 2. The stages of loading the sample under thermomechanical action

	Loading stage
	0	1	2	3	4	5	6	7	8
Load N, kg	0	345.39	345.39	345.39	345.39	345.39	345.39	426.39	515.09
Thermocouple readings, °С	22	22	60	90	115	120	125	130	130

2.2 Numerical simulation of the test

Расчет производился в конечно-элементном комплексе ANSYS Workbench.

Рассматривается трехслойная стеклопластиковая оболочка с размерами, указанными в п.п.2.1

В расчете средний слой легкого заполнителя (минераловатная плита) учитывается в работе конструкции оболочки.

Для упрощения расчетной схемы и ускорения расчета модель обрезана плоскостями симметрии, на обрезы наложены соответствующие граничные условия.

Общий вид расчетной модели после рассечения по осям симметрии с разбиением на конечные элементы (КЭ) приведены на Рисунке 3.

Схема проекта приведена на Рисунке 4. Основные этапы КЭ-ого расчета:

• •    создание геометрии конструкции;

• •    задание параметров материалов;

• •    задание граничных условий модели, разбиение ее на КЭ;

• •    задание параметров для термомеханического расчета и непосредственно сам расчет;

• •    передача результатов термомеханического расчета в модуль статического анализа и дополнение модели механическими нагрузками (собственным весом и весом пригруза), выполнение статического расчета;

Создание параметрической модели производится в модуле ANSYS DesignModeler.

Задание материалов производится в модуле термического анализа в разделе Engineering Data.

AD

Geometry

□ Geometry

$3 Parameters

Geometry

Рис. 3 – Расчетная модель ANSYS Steady-State Thermal / Static Structural

Fig. 3 – ANSYS Steady-State Thermal / Static Structural Calculation Model

▼	AE
1	В Steady-State Thermal
2	Engineering Data	z j
3	□ Geometry           -	z j
4	^ Model	' J
5	Й Setup	Z A
6	^ Solution	Z J
7	Ф Results	Z J
8	tp3 Parameters

Thermal analysis

AF
I “ Static Structural          I
^ Engineering Data
□ Geometry	z ^
^ Model	z J
Д Setup	z Л
^ Solution	z J
^ Results	/ .
$3 Parameters

Structural analysis

[W Parameter Set

Рис. 4 – Схема проекта ANSYS Workbench

Fig. 4 – The scheme of the ANSYS Workbench project

Параметры для основного несущего материала - стеклопластика принимаются по результатам лабораторных испытаний (после проведенного эксперимента из образца трубы были вырезаны участки для получения истинного модуля упругости материала, используемого в предоставленном изделии). В первом приближении материал как среднего слоя, так и внешних стеклопластиковых слоев рассматривается как изотропный, коэффициент линейного температурного расширения (КЛТР) для обшивок принимается по экспериментальным данным из работы [30]. Характеристики используемых материалов приведены на Рисунках 6–8.

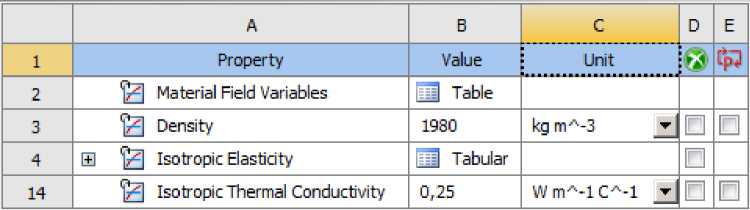
Рис. 5 - Общие параметры материала – стеклопластика

Fig. 5 - General parameters of the material – fiberglass

Modulus МО’) [Pa

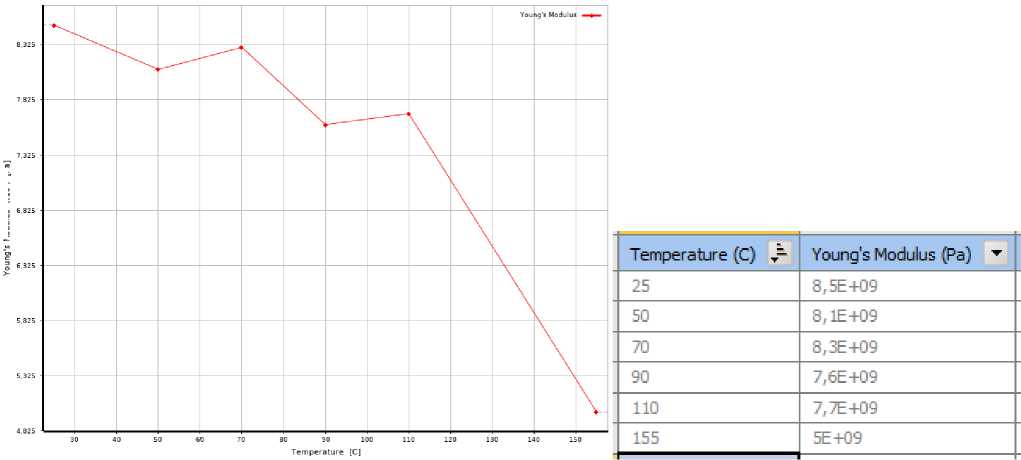
Рис. 6 - Параметры материала обшивок по результатам испытаний вырезанных образцов

Fig. 6 - Parameters of the cladding material according to the test results of the cut samples

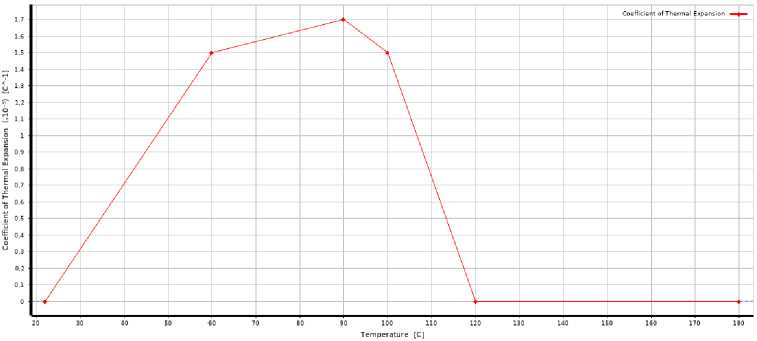
Рис. 7 - Изменение КЛТР стеклопластика в зависимости от температуры

Fig. 7 - The change in the temperature of fiberglass depending on the temperature

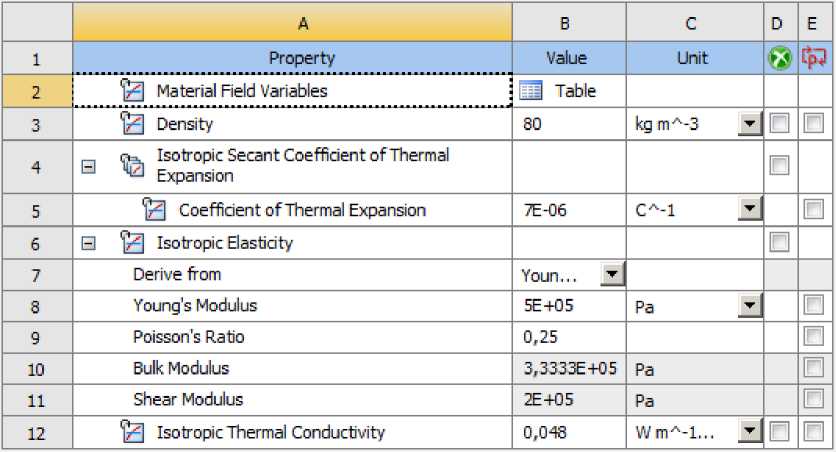
Рис. 8 - Параметры материала среднего слоя – минеральной ваты

Fig. 8 - Material parameters of the middle layer – mineral wool

Для материала опор-ложементов используется материал – сталь с параметрами, заданными в программе по умолчанию (Structural Steel).

Модель состоит из объемных КЭ. Для всех элементов модели используется КЭ «SOLID186» . Взаимосвязь объемов друг с другом задается через контакты их поверхностей . Для описания зоны контакта используется КЭ «CONTA 174».

Для всех контактных поверхностей, кроме контактов оболочки с опорами, задается полная склейка. Коэффициент трения между оболочкой и опорами принимается равным 0.3; между оболочкой и стропами подвеса 0.6.

Разбиение модели на сетку КЭ производится встроенным модулем ANSYS Mesh с добавлением дополнительного метода – «MultiZone» и функции «Face Meshing» для улучшения качества сетки. Размер КЭ принят 0.025 м.

Термический расчет производится в модуле ANSYS Steady-State Thermal. Целью расчета в нем в рамках данного исследования является получение градиента распределения температур по толщине оболочки для дальнейшей его передачи в модуль Static Structural, для учета температурного расширения материалов и изменения учета изменения модуля упругости обшивки с изменением температуры.

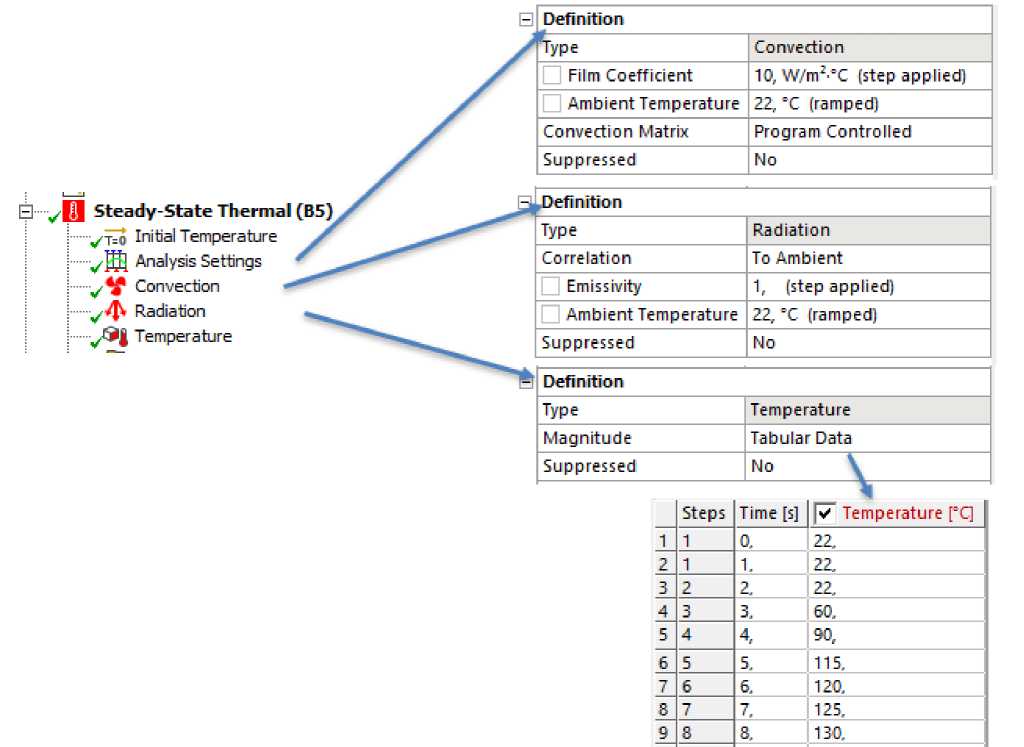
В качестве граничных условий для термического расчета принимаются: температура внутренней поверхности газохода как основное воздействие и тепловой поток по внешней поверхности и излучение тепла (лучистый теплообмен) через нее в качестве внешних факторов. Конкретные граничные условия и параметры расчета приведены на Рисунке 9.

Статический расчет производится в модуле ANSYS Static Structural.

Задача разбивается на три шага: на первом прикладывается статическая нагрузка, на втором – градиент температур, на третьем при установившемся градиенте увеличивается нагрузка. В общих настройках расчета добавлены функции «Weak Springs» (слабые пружины) и «Large Deflection» для избежания ошибок (связанные в первую очередь с наличием контактных поверхностей) при расчете.

В уИ Steady-State Thermal (В5)

j......y^o Initial Temperature / j......уЩ Analysis Settings j......у У Convection i......уф Radiation

I i......v^i Temperature

Steps Time [s]

120,

125,

130,

Рис. 9 – Граничные условия термического расчета

Definition ’'Type Convection Film Coefficient 10, W/m2°C (step applied) Ambient Temperature 22, °C (ramped) Convection Matrix Program Controlled Suppressed No Definition Type Radiation Correlation To Ambient Emissivity 1, (step applied) Ambient Temperature 22, °C (ramped) Suppressed No Definition Type Temperature Magnitude Tabular Data Suppressed No     \ p" Temperature [=C]

Fig. 9 – Boundary conditions of thermal calculation

В качестве нагрузок рассматриваются собственный вес и внешний пригруз. Первая формируется путем добавления в модель гравитации (нагрузка рассчитывается исходя из ускорения свободного падения и плотности материалов), вторая – прикладывается к плоскости обреза стропа. Граничные условия в статическом расчете – полные закрепления опор от смещений и поворотов по их внешней поверхности. На Рисунке 10 показаны зоны модели, на которые наложены условия симметрии.

Рис. 10 – Граничные условия симметрии модели

Fig. 10 – Boundary conditions of the symmetry of the model

Температурные воздействия, импортируются из термического расчета в формате градиента распределения температур.

В качестве выходных параметров рассматриваются перемещения вдоль оси Z (по вертикали) точек модели, соответствующих датчикам на реальной конструкции.

3 Results and Discussion

Основные результаты испытаний приведены в Таблице 3 (для испытания без температурного воздействия) и Таблице 4 (для испытания с нагревом внутреннего слоя оболочки). Для сравнения прогибов образца в реальной и КЭ-ой постановке испытания использовались показания датчика 3.1в.пр и соответствующая точка КЭ-ой модели.

Таблица 3. Результаты испытания образца без температурного воздействия

Table 3. Test results of the sample without temperature exposure

Sensor	Displacement of characteristic points, at load, kg
	0	85	174.4	260.44	345.39	426.39	515.09
1.1v.op	0.00	0.39	1.06	1.99	2.85	3.77	4.60
1.2v.op	0.00	0.77	1.63	2.69	3.68	4.65	5.72
2.1v.pr	0.00	0.51	1.54	2.71	3.88	5.08	6.41
2.2v.pr	0.00	0.87	1.73	2.95	4.09	5.28	6.56
3.1v.pr	0.00	0.94	2.30	3.64	4.86	6.18	7.68
4.1n.pr	0.00	0.77	1.75	2.88	3.93	5.00	6.13
4.2n.pr	0.00	0.65	1.47	2.38	3.18	4.11	5.06

Таблица 4. Результаты испытания образца при термомеханическом воздействии

Table 4. Результаты испытания образца при термомеханическом воздействии

Sensor	Displacement of characteristic points, at load, kg
	0	345.39	345.39	345.39	345.39	345.39	345.39	426.39	515.09

1.1v.op	0.00	2.72	2.81	3.12	3.40	3.64	3.93	4.73	-
1.2v.op	0.00	3.64	3.74	3.90	4.20	4.55	5.13	6.32	-
2.1v.pr	0.00	4.16	4.36	4.77	5.68	6.27	6.87	8.37	-
2.2v.pr	0.00	4.92	5.23	5.60	6.40	6.94	7.50	8.98	-
3.1v.pr	0.00	4.89	4.97	5.42	6.47	7.17	7.83	8.53	-
4.1n.pr	0.00	3.85	4.08	4.48	5.25	5.65	6.08	7.37	-
4.2n.pr	0.00	3.23	3.47	3.53	3.21	3.36	3.75	4.89	-
term.1	22	22	60	90	115	120	125	130	130
term.2	22	22	60	90	115	120	125	130	130
term.3	22	22	60	90	115	120	125	130	130

Перемещения точек КЭ-ой модели оболочки приведены в Таблице 5 и Таблице 6.

Таблица 5. Результаты КЭ-ого моделирования испытания без температурного воздействия

Table 5. The results of the Finite Elements (FE) simulation of the test without temperature exposure

Sensor	Displacement of characteristic points, at load, kg
	0	85	174.4	260.44	345.39	426.39	515.09
1.1v.op	0.00	0.85	1.95	2.98	4.00	4.98	6.09
1.2v.op	0.00	0.85	1.95	2.98	4.00	4.98	6.09
2.1v.pr	0.00	0.61	1.46	2.30	3.15	3.97	4.90
2.2v.pr	0.00	0.61	1.46	2.30	3.15	3.97	4.90
3.1v.pr	0.00	0.60	1.44	2.28	3.13	3.97	4.90
4.1n.pr	0.00	0.50	1.20	1.91	2.63	3.34	4.14
4.2n.pr	0.00	0.50	1.20	1.91	2.63	3.34	4.14

Таблица 6. Результаты КЭ-ого моделирования испытания при термомеханическом воздействии

Table 6. The results of the FE simulation of the thermomechanical impact test

Sensor	Displacement of characteristic points, at load, kg
	0	345.39	345.39	345.39	345.39	345.39	345.39	426.39	515.09
1.1v.op	0.00	4.30	4.27	4.32	4.66	4.82	4.94	6.07	7.33
1.2v.op	0.00	4.30	4.27	4.32	4.66	4.82	4.94	6.07	7.33
2.1v.pr	0.00	3.37	3.33	3.40	3.99	4.16	4.27	5.13	6.15
2.2v.pr	0.00	3.37	3.33	3.40	3.99	4.16	4.27	5.13	6.15
3.1v.pr	0.00	3.36	3.32	3.39	4.01	4.18	4.29	5.15	6.18
4.1n.pr	0.00	2.79	2.79	2.83	3.44	3.61	3.68	4.27	5.22

4.2n.pr	0.00	2.79	2.79	2.83	3.44	3.61	3.68	4.27	5.22
term.1	22	22	60	90	115	120	125	130	130
term.2	22	22	60	90	115	120	125	130	130
term.3	22	22	60	90	115	120	125	130	130

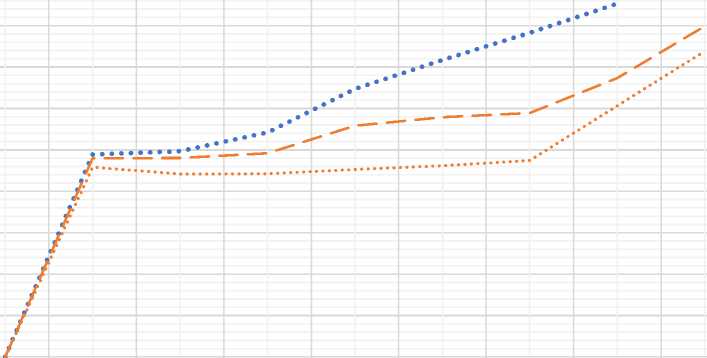
Ниже на Рисунке 12 и Рисунке 13 приведены графики отражающие показания датчика 3.1в.пр для расчета и испытания без учета температурного воздействия и с ним соответсвенно.

По графикамм видна общая тенденция – КЭ расчет показывает прогибы, практически идентичные реальному испытанию. В среднем расхождение расчета с испытанием при механическом воздействии составляет 1.8%.

Сравнительный анализ результатов реального испытания и его КЭ модели при комбинированном термомеханическом воздействии приведен на Рисунке 11. Максимальное расхождение наблюдалось на третьем шаге, при температуре 125°С – 24.8%, минимальное, при отсутствии термического воздействия – 1.8%. Такие величины расхождений можно связать с начальными несовершенствами представленного для испытаний образца. Тем не менее, общий вид графика прогибов, полученного в ходе КЭ расчета, повторяет аналогичный график, полученный в ходе испытания.

The discrepancy between the test and the FE simulation

30.0

25.0

20.0

^o

0s

15.0

СП

Q

10.0

5.0

0.0

^^^^m Discrepancy

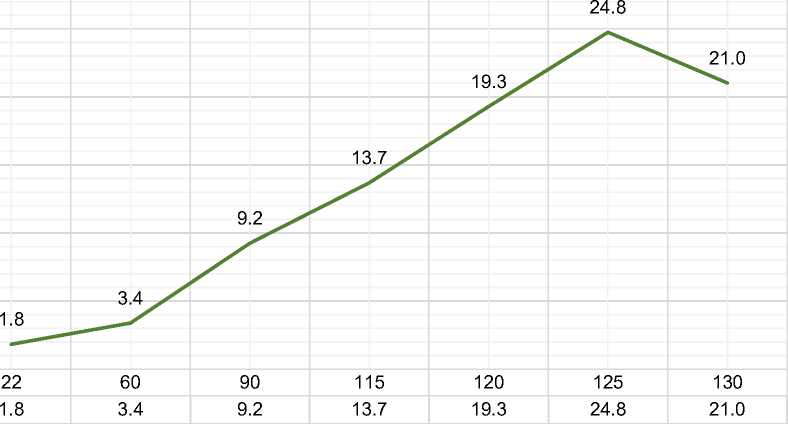
Рисунок. 11 – График расхождения в результатах реального и КЭ эксперимента

Fig. 11 – A graph of the discrepancy between the results of the real and the FE experiment

Displacement for point 3 without heating

9.00

8.00

7.00

6.00

Ф E ф о го

Q

5.00

4.00

3.00

2.00

1.00 0.00			174.4	260.44	345.39	426.39	515.09
	.1
	0	85
Test	0.00	0.94	2.30	3.64	4.86	6.18	7.68
Test*	0.99	2.43	3.86	4.94	6.01	6.85	7.68
FE full	0.00	1.61	2.92	4.15	5.38	6.58	7.93

Рис. 12 – График перемещений точки 3 при механическом воздействии (Test* - линия разгрузки)

Fig. 12 – Graph of point 3 displacements under mechanical action (Test* - unloading line)

Displacement for point 3 with heating

9.00

8.00

7.00

6.00

Ф E ф о го

5.00

4.00

<л

3.00

2.00

1.00

0.00	0	345.39	345.39	345.39	345.39	345.39	345.39	426.39	515.09
Test	0.00	4.89	4.97	5.42	6.47	7.17	7.83	8.53
FE full	0.00	4.80	4.80	4.92	5.58	5.79	5.89	6.74	7.99
FE no KLTE	0.00	4.58	4.42	4.42	4.53	4.62	4.74	6.06	7.39

Рис. 13 – График перемещений точки 3 при термомеханическом воздействии (FE no KLTE -(coefficient of linear temperature expansion) – перемещения в модели без учета КЛТР) Fig. 13 – Graph of point 3 displacements under thermomechanical influence (FE no KLTE -(coefficient of linear temperature expansion) – displacement in the model without considering KLTE)

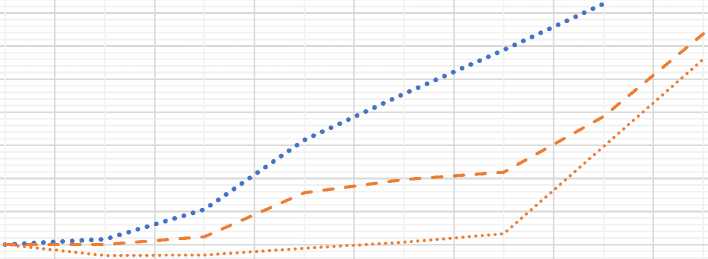
Влияние нагрева внутренней обшивки на прогибы оценивалось следующим образом: из итогового значения прогибов на каждом шаге вычиталось значение прогиба на первом шаге нагружения, когда нагрев отсутствовал. По полученным значениям был построен график зависимости прогибов оболочки при постоянной нагрузке от температуры внутренней обшивки (Рисунок 14). По нему видно, что на при температурах до, приблизительно, 90°С прогибы практически не увеличиваются.

ф

ф

ф

ф CL ф

4.00

3.50

3.00

2.50

2.00

1.50

1.00

Перемещение т.3 при постоянной нагрузке с учетом t

0.50

0.00

-0.50	22	60	90	115	120	125	130	130
Test	0.00	0.08	0.53	1.58	2.28	2.94	3.64
FE full	0.00	0.00	0.12	0.78	0.99	1.09	1.94	3.19
FE no KLTE	0.00	-0.17	-0.16	-0.06	0.04	0.16	1.48	2.80

Fig. 14 – График перемещений точки 3 при постоянной нагрузке и переменной температуре

(FE no KLTE – перемещения в модели без учета КЛТР)

Fig. 14 – Graph of point 3 displacements at constant load and variable temperature (FE no KLTE – movements in the model without considering KLTR)

После отметки в 90°С на графике прогибов наблюдается излом. Он явно видел на графике расчетных прогибов и менее заметен в реальном испытании. Для того, чтобы понять причину резкого возрастания прогибов на отдельном участке температур, был построен аналогичный график перемещений, но для расчетной модели, в которой КЛТР материала обшивок был принят равным 0. На Рисунках 13 и 14 можно видеть, что при отсутствии температурного расширения излома на графике также нет. Следовательно, можно предполагать, что резкий рост прогибов на участке 90-115°С вязан с падением на этом диапазоне температур значения КЛТР стеклопластика практически до 0.

В ходе натурного испытания при нагрузке 515.09 кг прогибы образца начали ускоренно расти в течение нескольких минут, после чего произошло разрушение обшивок и складывание оболочки по центру пролета (Рисунок 15 слева). В месте излома присутствует расслоение обшивок. Учитывая место расположения и характер излома, а также характеристики материалов обшивок можно утверждать, что при нагреве значительная часть усилий от внешней нагрузки перешла на наружный слой (Рисунок 16). Ввиду этого в центре пролета при указанной нагрузке внешний слой потерял несущую способность, что привело к разрывам в армирующей ткани и постепенному нарастанию деформаций без увеличения внешней нагрузки. Внутренний слой из-за пониженных (с ростом температуры) характеристик не смог полностью воспринять усилия от частично разрушенного внешнего слоя. По достижению определенной степени разрушения внешней обшивки наступило полное исчерпание несущей способности образца.

Рис. 15 – Общий вод разрушения опытного образца оболочки (слева – непосредственно после разрушения, справа – после снятия слоя шпаклевки)

Fig. 15 – The total volume of destruction of the prototype shell (on the left – immediately after destruction, on the right – after removing the putty layer)

Изополя напряжений, полученные в ходе КЭ-ого моделирования (Рисунок 16) эксперимента указывают, что разрушение образца должно было произойти на опоре в зоне над ложементом. Но в условиях реального испытания такого не произошло. Объяснить подобное различие можно неплотным опиранием реального образца на ложементы и наличием слоя штукатурки на наружной поверхности оболочки, смягчающей данной контакт.

Необходимо отметить, что модель участка газоотводящего тракта, представленная для натурного испытания, содержала ряд дефектов, которые отразились на результатах. Например: различные диаметры торцевых сечений; неравномерность и неоднородность утеплителя (данный дефект мог повлиять в значительной мере на совместность работы слоев); на одном из концов трубы внутренняя поверхность «пошла волной» (что также в значительной мере могла повлиять на работу трубы в приопорной зоне); неплотное опирание торцов образца на опоры.

Расчет трехслойной оболочки методом конечных элементов на механическое воздействие показывает хорошую сходимость с реальным испытанием. В случае комбинированного термомеханического воздействия качественно результаты также близки, но конкретные значения прогибов различаются, и разница между ними растет с ростом температуры.

При температурах до 90°С влияние нагрева внутренней поверхности трубы на ее прогиб мало. На участке 90-120°С наблюдается резкое увеличение прогибов, которое можно связать с падением на данном участке значения КЛТР материала обшивок практически до 0. При дальнейшем нагреве характер деформаций линейный.

Различия в результатах расчета и испытания можно объяснить наличием в реальном образце ползучести, которая не учитывалась в КЭ расчете. Особенно это актуально при термомеханическом воздействии, где данный эффект потенциально более значим, чем в случае нагружения без нагрева.

C: Copy of НДС

Equivalent Stress 4

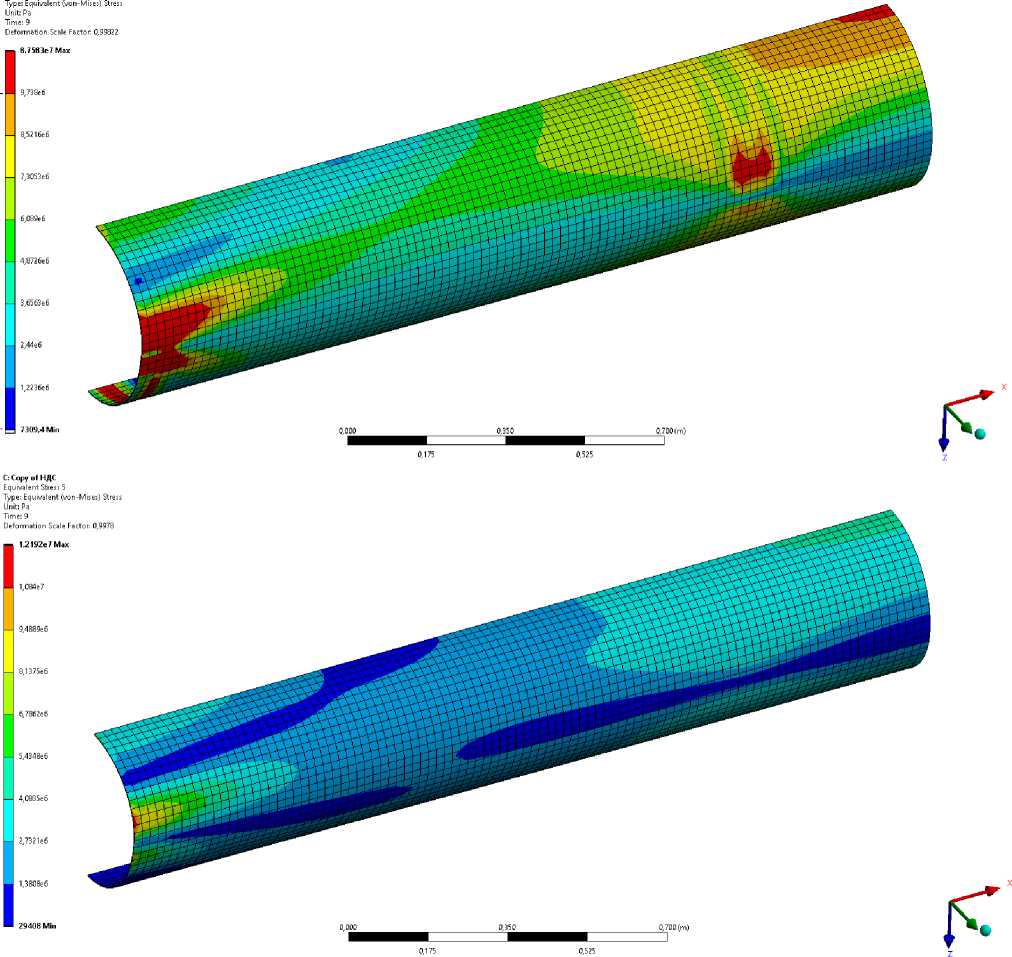
Рис. 16 – Изополя эквивалентных напряжений по Мизесу для внешней (сверху) и внутренней (снизу) обшивки

Fig. 16 – Isofields of equivalent Mises stresses for the outer (top) and inner (bottom) skin

4 Conclusions

Основные выводы по работе:

• 1)    разработана и верифицирована испытаниями конечно-элементная модель участка трехслойной стеклопластиковой оболочки, работающей по неразрезной схеме;

• 2)    при температурах до 90°С влияние нагрева внутренней поверхности трубы на ее прогиб незначительно;

• 3)    на участке температур 90-120°С имеет место резкое скачкообразное увеличение прогибов оболочки, связанное с падением КЛТР материала обшивок;

• 4)    при расчете трехслойных стеклопластиковых оболочек необходимо учитывать температурное расширение материалов обшивок, расчет без учета данного фактора не является расчетом «в запас»;

• 5)    при температурах эксплуатации ниже 90°С учетом изменения КЛТР в зависимости от температуры можно пренебречь.

Учитывая вышесказанное, создание рабочей расчетной модели требуется проведение более комплексного анализа напряженно-деформированного состояния рассмотренной оболочки и уточнения ряда параметров материала обшивок, в частности ползучести.