Триангуляция пространственных элементарных областей

DOI:

Пусть задан конечный набор точек { P , }^ в пространстве R ³ . Триангуляцией данного набора точек называется совокупность невырожденных тетраэдров { T j }Д 1 , удовлетворяющих условиям:

• 1)    любая точка P i является вершиной хотя бы одного тетраэдра T j ;

• 2)    каждый тетраэдр T j содержит только четыре точки из данного набора, являющиеся вершинами этого тетраэдра.

Пусть Q ограниченная область в R ³ . Триангуляцией области Q называется триангуляция произвольного конечного набора точек, лежащего в замыкании области Q.

В настоящее время для плоских областей имеется довольно большое число различных алгоритмов триангуляции, описание которых можно найти, например, в работах [1; 5; 8–10]. Многие из приведенных там алгоритмов подходят, после соответствующих изменений, и для трехмерных областей. Описание некоторых прямых и итерационных алгоритмов в пространственном случае имеется в работах [2; 3]. Как правило, в перечисленных работах не исследуется математически строго качество построенной триангуляции и не выводится никаких количественных оценок ее числовых характеристик.

В настоящей работе мы описываем достаточно простой в реализации алгоритм триангуляции пространственной области специального вида, который относится к так называемым прямым методам. Для оценки качества построенной триангуляции мы используем минимальный двугранный угол, вычисленный среди всех тетраэдров триангуляции. Именно мы приводим нижнюю оценку этого угла через геометрические характеристики области и параметры ее разбиения на ячейки. Стоит отметить, что условие пустой сферы, то есть условие Делоне, не обеспечивает качественной триангуляции (в отличие от триангуляции на плоскости). Например, в работе [6] строится пример триангуляции пространственной области, удовлетворяющей условию Делоне, но не аппроксимирующей с достаточной точностью градиент гладкой функции. Это ограничивает область применения таких триангуляций в различных вычислительных задачах, например, при численном решении уравнений с частными производными. В то же время более сильные условия на триангуляцию, которые обеспечивают необходимую точность вычисления площади, дают равномерную сходимость приближенных решений уравнения минимальной поверхности [4]. Для пространственных триангуляций (см., например, [7]) отделимость от нуля двугранных углов в тетраэдрах позволяет показать, что погрешность вычисления градиента гладкой функции стремится к нулю при стремлении к нулю максимального диаметра тетраэдров.

• 1.    Основные результаты

Рассмотрим элементарную область Q С R ³ , которая имеет вид

Q = {(х, у, z) : а < х < Ь, с < у < d, р(х, у) < z < ^(х, у)} , где р(х,у) и ^(х,у) — заданные на прямоугольнике [а, Ь] х [с, d] функции, удовлетворяющие условию Липшица.

Далее полагаем мо =, a inf г ,1(^(х,у) - р^у)) > 0, (ж,у)е[а,Ь]х[с,сг]

М 1 =     sup    (^(х, у) - р(х, у)) <  то .

(ж,у) е [а,Ь] х [с,сг]

Будем считать, что для функций р(х,у) и ^(х, у) найдется постоянная L <  то такая, что выполняются неравенства

| р ⁽ х ^{, ,}у ^{, ) -} р ⁽ х"^,у" ^{) |}<  ^L ^ ⁽х' ^- х" ^{) 2} + ⁽у' ^- у" ^{) 2} ,

1 Ф(х',у ' ) - ф(х ^, ,у ^,, ) | <  L ^ (х - х ‘‘ ) ² + (у' - у' ‘ ) ²

для любых ж ' , ж '' G [а, b], у ' , у ’’ Е [с, d]. Далее опишем построение триангуляции области Q. Пусть а = ж ₀ < ж ₁ < ж ₂ < ... < ж „ = b — разбиение отрезка [а, b], с = у ₀ <у ₁ < ж ₂ <  < ... <у _т = d — разбиение отрезка [с, d\. Положим

/ т (^ж,у) = т^(^ж,у) + (1 - 'Г^^у), ^т Е ^{[0 ,}1\.

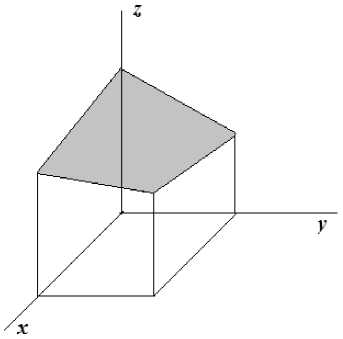
Рис. 1. Пример элементарной области Ω

Разобьем отрезок [0,1] точками 0 = т ₀ <  т ₁ <  т ₂ < ... <  т ^ = 1 ив области Q рассмотрим сетку, определяемую системой точек

A _ijl (ж i ,у j ,Z iji ) = (ж i ,у _j , Д (ж i ,у j )), i = 0,...,п, j = 0,...,т, l = 0, ...,&.

Ясно, что все точки (жi, уj,ziji) Е fi. Зафиксируем индексы i,j,l, где i = 0, ...,п — 1, j = 0,...,т — 1, l = 0, ...,к — 1 и рассмотрим ячейку, задаваемую точками Aijl, Ai+1jl, Aij+ii, Ai+ij+ii, Aiji+i, Ai+iji+i, Aij+ii+i, Ai+ij+ii+i. Данная ячейка fiiji определяется следующим образом fiiji = {(ж,у,ж) : Жi < ж < Жi+1, Уj <у < Уj+1, /т (ж, у) < Z < /тг+1 (ж, у)}.

В каждой такой подобласти fi _ij_i построим триангуляцию, состоящую из шести тетраэдров. Способ выбора этих тетраэдров для параллелепипеда указан в работе [3]. Мы используем ту же схему.

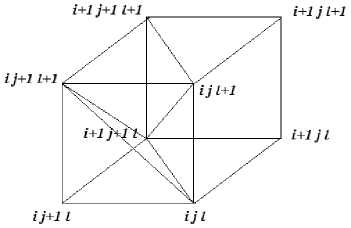
Рис. 2. Схема построения тетраэдров в одной части ячейки Q ^.,-;

Приведем эти тетраэдры, выписав четыре вершины каждого из них. Итак, полагаем ^ iji = ^{( A} iji , ^A ij+ii , ^A ij+ii+i , ^A i+ij+ii ), T i^ji = ^{( A} iji+i , ^A ij+ii+i , ^A i+ij+ii+i , ^A i+ij+ii ),

^ 37 = ^(v^ ijl , A ijl+1 , A i+1j+1l ,A ij+1l+1 ⁾, ^T-ijl     ⁽A ijl , A i+1j+1l , A i+1jl ,A i+1jl+1 ⁾,

^T i^jl     ⁽A ijl+1 , A i+1jl+1 , A i+1j+1l+1 , A i+1j+1l' ⁾, ^Tijl     ⁽A ijl , A i+1j+1l , A ijl+1 , A i+1jl+1 ^{) .}

Пробегая все допустимые значения индексов i,j,l, получим триангуляцию всего множества точек { A _ij_l } , i = 0,..., п, j = 0,..., т, l = 0,..., к.

Для формулировки основного результата введем следующие обозначения. Полагаем

hl

min (x _{i +1} — x _i ), h 2

0 < i < n - 1   ^{+             1}

max (X i+1 — X i ), 0 < i < n - 1

^h =

m ^min /y j+1 ^- y j ), ^hy 0y

max ⁽ y j+1 - y j ), 0 < j < m - 1

t ¹

min (t i +1 - t i ) , t ²

0

max (ti+1 - ti). 0

Оценка углов будет проводиться одинаково в каждой ячейки Q_ij-_l. Более того, ее достаточно получить только для тетраэдров T1j_l,T2j_l,T3j_l, так как для остальных трех рассуждения будут такими же.

Для начала отметим следующее. Пусть заданы два вектора

V1 = (ai, в1,1),V2 = (a2, в2,1).

Тогда синус угла θ между ними удовлетворяет неравенству

-

^(a1 ^{- a}2^{)2 + (в}1 ^{— в}2⁾² sin 6 >                               .

(1 + a1 + в1)(1 + a2 + в2)

Итак, рассмотрим первый тетраэдр T^. Его грани лежат на плоскостях, нормали которых равны векторам

V1 = (1, 0, 0), ^2 = (0,1, 0), У3 = (

^Zi+1j+1l

-

Xi+1

-

^Zij+1l  ^Zij+1l

,

Xi

yj+1

-

-

^Zijl yj ¹

-1 ,

_C4 -(

^Zi+1j+1l

-

^Zij+1l+1

^Zij+1l+1

-

Xi+1

-

Xi

,

yj+1

-

^Zijl

,

Уз

-1 .

Обозначим углы между соответствующими векторами 612, 613, 614, 623, 624, 634. Тогда, используя оценку (1), получаем для угла θ34 неравенство sin2 634 >

> (¹⁺(

^i+1j+1l-^ij+1l

^г+1

-

^i

(

Zij+U+1^-ij+П

li+1

-

^i

А + к ^zij + 1l + 1  ^zijl+1 А

Уз+1^-Уз    /

V + к гц+п-ггц А     1 + к

Уз+1^-'Уз

^i+1j+1l-^ij + 1l+1

^г+1 ^г

А I к ^ij + 1l + 1 ^ijl 'Уз+1^-,Уз

r) >

≥

(1 + 2L²) М + (

(§ )^{2 M +}L'²

^{L +}j^T^M1) ⁺(^{L + j}^r^M1) ^

Аналогично приходим к нижним оценкам остальных углов

sin²613

> -------,

>1 + L²,

sin²6₁₄

≥

1 + (ЙM1 + L)

₂, sin²612 = 1,

sin²023 —

1 + L²’

sin²024

^{1 +}(^ ^М1^{+ L})

Из углов других тетраэдров отличительными будут углы для граней, находящихся на

плоскости, ортогональной вектору 55 =

A yj+i-yj

Xi+l-Xj

-

1, о)

то есть на диагональной плос-

кости. Оценка угла 045 между векторами 54 и 55 будет такой

sin²0₄₅>

1 + (<М1 + L) + (§ M1 + L)

Остальные углы в оставшихся тетраэдрах оцениваются через те же величины. В итоге приходим к утверждению, которое показывает, что при определенных условиях на разбиения отрезков [а, Ь] и [с, d] при измельчении триангуляции двугранные углы построенных тетраэдров будут отделены от нуля некоторым положительным числом.

Теорема 1. Для любого двугранного угла θ всякого тетраэдра построенной триангуляции выполнено неравенство

М0 + L², X /

(§ )2 ^М0 + ^L,   + .'5

sin²0 >

(1 ^{+ 2L}2) (1 ⁺(£г^М1⁺l) + (^^М1⁺l) )

В частности, если п = т = к и х^ = а + г (Ь — а)/п, yj = с + 3 (d — с) /т, т = 1/к, то min] (^°-) +L2, (^°-) + L2,1+2L2 Ъ-а            , d-с            ,

²θ≥

-  (1+2L2)(1 + (ъ-а+L)2 + (d-а+L)²)

Наконец, для куба имеем sin2 0 — 1/3.