Трибоэлектрические явления и износ инструментальных материалов

Введение. Специфическая пара трения инструмент — деталь функционирует в условиях интенсивного тепловыделения, когда силовые и тепловые нагрузки действуют на контактных площадках ограниченных размеров при активном участии в процессе износа и внешней среды — жидкой или газообразной.

В условиях резания тепловое состояние режущего инструмента характеризуется большими числами Пекле (больше 10), значительными температурными градиентами по нормали к изнашиваемой поверхности, превалирующей ролью теплоотвода из зоны резания для поддержания оптимальной температуры, а также активным действием объёмных тепловых источников различной физической природы, поступающих от пластических деформаций в детали при обработке пластичных материалов, от структурно-фазовых превращений, от эндо- и экзотермических превращений в компонентах смазочно-охлаждающих средств, от реакций окисления материала и др.

Приведённые тепловые источники относятся к классу объёмных, действующих на определённой глубине поверхностного слоя, и измеряются единицами и десятками микрон. Определённый вклад в изучение тепловых процессов применительно к трению в условиях резания внесли исследования [1—14], в которых установлена связь температурного градиента с интенсивностью изнашивания.

Целью данной работы является изучение и обобщение внутренних источников изменения энергетического, теплового состояния изнашиваемого материала пар трения.

Трибоэлектрические явления в специфической паре трения инструмент — деталь. Известно, что термоЭДС — относительная электродвижущая сила в электрической цепи, составленной из последовательно соединённых разнородных металлов, чрезвычайно чувствительна к малейшим изменениям их состава или состояния. Если контакты поддерживаются при разных температурах 71 и Т (явление Зеебека), то

Е = ohT,

где о — коэффициент термоЭДС, В/°С; ЕТ= Т₂ - Ту — перепад температур по длине цепи; Е— термоЭДС, В.

Знак при о обычно связан с формой поверхности Ферми, поэтому даже для чистых металлов значение о определяют экспериментально [15].

Обратным явлению Зеебека является явление Пельтье [16], заключающееся в том, что при прохождении тока I в цепи из разнородных проводников в местах их контакта в дополнение к теплоте Джоуля в единицу времени выделяется или поглощается (в зависимости от направления тока) количество тепла, пропорциональное прошедшему через контакт количеству электричества и некоторому коэффициенту п, зависящему от природы материалов, qn = nl (2)

Если вдоль проводника с током существует градиент температуры дТ / Эх, то в объёме проводника в дополнение к теплу Джоуля в единицу времени выделяется или поглощается, в зависимости от направления тока, некоторое количество тепла (эффект Томсона):

д_г=(тдТ/дх)1. (3)

Между указанными термоэлектрическими эффектами существует термодинамическая связь, обнаруженная Томсоном [15]. Согласно Томсону, интегральная термоЭДС Е пары двух металлов а и b равна

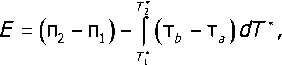
гдет/, и та — коэффициенты Томсона для металлов b и а; Т* и Т* — абсолютные температуры холодного и горячего спаев.

В случае обратимого кругового процесса перемещения тепла по замкнутому контуру при протекании тока Томсоном получено выражение

^2 _ ^1 [ _ Г "*"а £j_T* _ Q

/2    1^ ) у, 1

которое после дифференцирования (4) и (5) приводит к dE п df."e"T, dE _ dn / dT/df, а также связи между теплом Томсона и термоЭДС:

d2E , ч

В выражениях (6), (7) п — относительный коэффициент Пельтье для пары проводников; е — относительная дифференциальная термоЭДС пары; т — относительный коэффициент Томсона; знаком * при температуре здесь и далее обозначена абсолютная температура.

Если Е— относительная интегральная термоЭДС пары проводников, то согласно [17]:

Е = Е_ь - Еа, е = £ь- £а, П = П/, - п_а; т = Т/, - т_а.                   (9)

Здесь £/, и £а — абсолютные дифференциальные термоЭДС материалов пары.

Показано [15], что абсолютная термоЭДС Т.

имеет значение энтропии, ЭДС Томсона т — теплоёмкости движущихся носителей тока, а коэффициент Пельтье — связанной энергии.

Определим влияние эффектов Томсона и Пельтье на тепловой режим пар трения инструмент — сталь. Данные по значениям £, п, т для инструментальных и обрабатываемых материалов отсутствуют, их определяли расчётно-экспериментальным методом [18].

Расчёт термоэлектрических характеристик инструментальных и конструкционных материалов. Термодинамические соотношения между термоэлектрическими эффектами (6), (7) и зависимостью (8) дают возможность рассчитать абсолютные значения £, п, т для каждого материала, если известна относительная интегральная термоЭДС между материалом и эталоном (обычно Pt или Си). Зависимость Еот температуры находилась путём тарирования с использованием экспериментальных зависимостей ЕхП = f(T) (рис. 1), известных для каждого сплава. Ап- проксимирующую функцию ЕХР1 = f(7) с относительной ошибкой ± 2 % находили с использованием стандартной программы. Наиболее подходящей аппроксимирующей кривой является полином четвёртого порядка относительно Е (для всех инструментальных и обрабатываемых материалов). При этом абсолютная дифференциальная термоЭДС материала равна

£х = ех,и - ^t.                                            (11)

Аппроксимация температурной зависимости абсолютной термоЭДС с последующим дифференцированием функции £х = f(7) даёт в соответствии с (8) величину коэффициента Томсона:

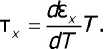
При известных г_х, согласно (6), коэффициент Пельтье принимает вид: п_х=е_хТ.                                    (13)

В табл. 1 приведены уравнения аппроксимирующих функций для расчёта термоэлектриче ских характеристик твёрдого сплава Т15К6 (Т = 100—1000 °C); на рис. 2 показано влияние тем

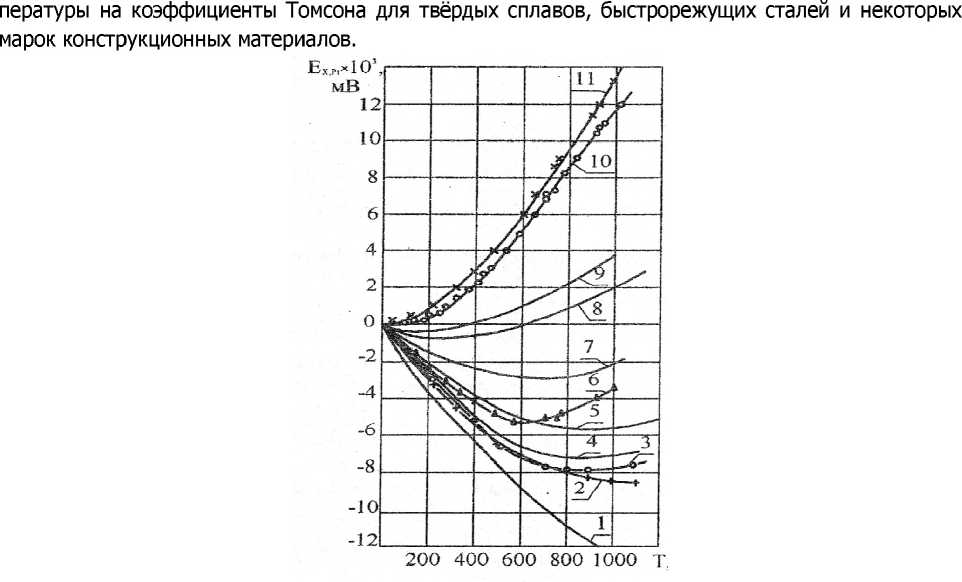
Рис. 1. Зависимость термоЭДС твёрдых сплавов относительно платины: 1 — ВК4, 2 — ВК6, 3 — ВК6М, 4 — ВК8, 5 — Т5К10, 6 — ВК15М, 7 — Т15К6, 8 — Т30К4, 9 — Т60К6, 10 — МНТ-А2, 11 — КТН-16

Таблица 1

Абсолютные значения термоэлектрических характеристик для твёрдого сплава Т15К6 (Т= 100-1000 °C)

Характеристика	Уравнения аппроксимирующих функций
Е=^Т) £=fm п = Г(7) т=Г(7)	Е = 0Д77"103 - 0Д18-102Т+ ОДбг-Ю"1?2 + ОЛЗЗ-Ю"5?3 - ОДЗв-Ю"8?4 £ = -0,155-10-2 - 0,271-10-1Г+ О^ОЭ-Ю"4?2 - О^ЗБ-Ю7?3 + 0Д49-10-1°74 п = -0,379'Ю4 - 0,274'102Т+ ОДЭЗ-Ю"1?2 - ОДОЭ-Ю"4?3 - ОДИ-Ю"8?4 т = -0,740-Ю1 + 0,617-10‘2Т+ ОДЗО'Ю^Т2 - 0Д44-10‘б73 + ОДЭБ-Ю"10?4

Как следует из полученных результатов, значения т претерпевают инверсию, особенно чётко проявляющуюся для быстрорежущих сталей и однокарбидных твёрдых сплавов. Сплавы группы ВК имеют т = 0 в двух температурных диапазонах: 200...300 °C и 700...850 °C; максималь ные положительные значения т у них соответствуют температурам 500...650 °C (рис. 2, а)

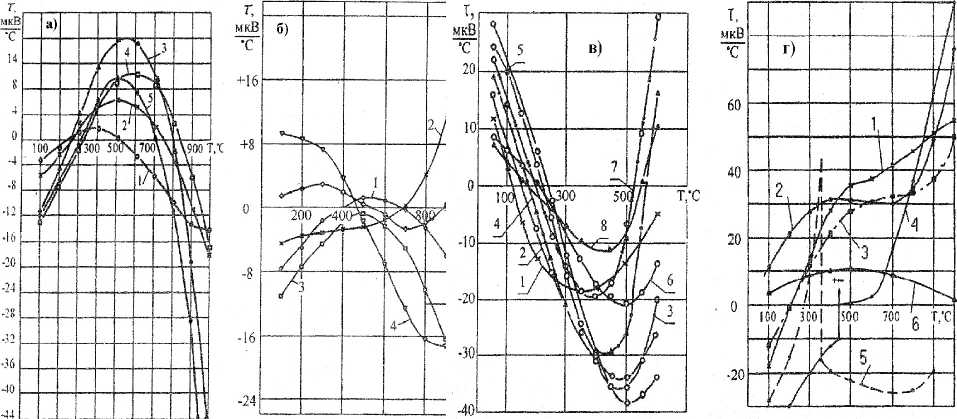
Рис. 2. Зависимость коэффициента Томсона от температуры для: а — однокарбидных твёрдых сплавов: 1 — ВК4, 2 — ВК6, 3 — ВК6М, 4 — ВК8, 5 — ВК15М; б — двухкарбидных и безвольфрамовых твёрдых сплавов: 1 — Т5К10, 2 — Т15К6, 3 — Т60К6, 4 — МНТ-А2, 5 — КНТ-16; в — быстрорежущих сталей: 1 — Р6М5, 2 — Р18, 3 — Р9Ф5, 4 — Р6М4Ф4, 5 — Р8МЗФ4, 6 — Р4М4Ф4, 7 — Р18Ф2К8МЗ, 8 — Р6Ф2К8М5; г — некоторых чистых металлов и карбидов: 1 — карбид вольфрама, 2 — карбид титана, 3 — карбид тантала, 4 — кобальт, 5 — никель, 6 — молибден

Для двухкарбидных и безвольфрамовых сплавов абсолютные значения т ниже, чем у твёрдых сплавов группы ВК; экстремумы менее выражены у безвольфрамовых сплавов (рис. 2, б). Для быстрорежущих сталей (рис. 2, в) характерен отрицательный максимум кривых т = f (7) при температурах 400...500 °C, а также нулевые значения т в диапазоне 150...250 °C и 550...650 °C. Из представленных данных видно, что значение т у инструментальных материалов разных групп находятся в пределах от +30 до -40 мкВ/°С.

Данные по ЭДС Томсона для карбидов WC, TiC и ТаС получены расчётом по данным для зависимостей Е = ГСП в паре с вольфрамовым стержнем. По-видимому, максимумы значений т для сплавов группы ВК и ТК обусловлены влиянием кобальта, у которого ЭДС Томсона принимает значение +оо при температуре 447 °C аллотропического превращения о-Со^р-Со [15]. Свойства карбидов влияния здесь не оказывают, поскольку с ростом температуры значение т у них монотонно возрастает в положительной области значений (рис. 2, г). Подтверждением такому предположению может служить другой характер изменения т у безвольфрамовых сплавов, не содержащих кобальт. У сплавов, имеющих никелево-молибденовую связку, заметна аналогия хода кривых т = f (7) для сплавов МНТ-А2 и КНТ-16 (рис. 2, б, кривые 4 и 5) и чистых Ni и Мо (рис. 2, г, кривые 5и 6).

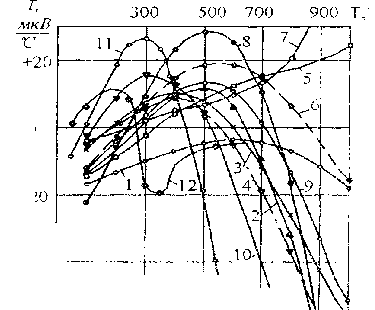
Для конструкционных материалов разных групп значения т изменяются от +30 до -100 мкВ/°С (рис. 3) и для большинства из них имеют положительный максимум при температурах 400...500 °C, а нулевые значения — в двух диапазонах температур: -150...250 °C и 550...750 °C.

Значения теплот Пельтье у инструментальных материалов колеблются от +5"10³ до -35"10³ мкВ, причём у твёрдых сплавов групп ВК и ТК значения коэффициента п находятся в отрицательной области, для быстрорежущих сталей — в положительной, с явным максимумом при Т = 300°.

Оценка влияния объёмных источников тепла Томсона. Для определения мощности объёмных источников тепла Томсона необходимо знать знак при т, а также направление тока, протекающего через фрикционный контакт. Применительно к контакту в условиях трения разнородных металлических материалов, можно с учётом вышесказанного и найденных значений т определить направление ЭДС Томсона для каждого из тел пары трения. Например, для пары Т15К6 — Ст35 в диапазоне температур контакта 100—710 °C у Т15К6 коэффициент Томсона отрицателен, значит, ЭДС Томсона направлена от зоны контакта, где температура максимальна, в тело пластины твёрдого сплава; для Ст35 ЭДС Томсона отрицательна во всём диапазоне температур и также направлена вглубь контртела.

г мкВ

500 700

Рис. 3. Зависимость коэффициента Томсона от температуры для конструкционных материалов: 1 — Ст35; 2 — 1X18H9T;

• 3 — Ст45; 4 — Ст7; 5 — ВТЗ-1; 6 — ОТ4; 7 — X17H20TP; 8 — 40ХНМА; 9 — ЭИ481; 10 — ЗОХГСА; 11 — СЧ 18-36; 12 — ЛС 58-1Л

Тепловой эффект Томсона определяется направлением тока — точнее, направлением потока электронов. Если по проводнику, вдоль которого существует градиент температуры, протекает электрический ток, направление которого соответствует движению электронов от горячего конца к холодному, то, переходя из более горячего участка в более холодный, электроны передают избыточную энергию окружающим атомам, что вызывает нагрев проводника (тепло выделяется) [17, 19]. При обратном направлении тока электроны пополняют свою энергию за счёт окружающих атомов и охлаждают объём (поглощение тепла). В приведённой упрощённой трактовке эффекта Томсона не учитывается тот факт, что в первом случае электроны тормозятся, а во втором ускоряются полем термоЭДС, что может не только изменить значение коэффициента Томсона, но и привести к перемене его знака.

В условиях изнашивания инструментальных материалов токовый режим пары трения создаётся циркуляцией через зону трения естественно возникающих трибоэлектрических токов и путём пропускания постоянного тока от постороннего источника. В некоторых случаях созданием специальных условий можно обеспечить режим максимальной отдачи мощности термоэлементом зоны трения.

В общем случае, независимо от этих вариантов, рассмотрим тепловой эффект Томсона в зоне трения для двух направлений тока — от инструментального материала к контртелу и наоборот. Направление потока электронов, естественно, будет противоположно направлению тока. Для качественной практической оценки теплового действия эффекта Томсона необходимо иметь в виду простое правило: если направление потока электронов через фрикционный контакт совпадает с направлением коэффициента (ЭДС) Томсона материала пары трения, его объём дополнительно нагревается, при встречных направлениях потока электронов и ЭДС Томсона объём материала будет охлаждаться.

Расчёт мощности объёмных источников тепла Томсона в элементах пары трения. Для теоретической оценки вклада эффекта Томсона в тепловое состояние зоны трения (температура контактной поверхности, распределение температур по нормали к трущейся поверхности, величина градиента) необходимо знать кроме направления теплового действия мощность объёмных источников тепла Томсона. Для этого, чтобы рассчитать мощность тепловыделения на контакте q, Вт/м², от сил трения, необходимо учесть фактическое контактное давление, которое при пластическом контакте приближается к твёрдости наиболее мягкого материала пары [20]. Для оценки площадки фактического контакта используют приближённую зависимость [21]:

A_r=N/HV,                                (14)

где /V— нормальная нагрузка; HV— микротвёрдость наиболее мягкого материала пары трения.

В настоящем исследовании в качестве материалов контртела применялись Ст35,1Х18Н9Т, ВТЗ-1, СЧ18-36, микротвёрдости которых соответственно равны 3200, 3500, 3700 и 2000 МПа. Рассчитанные по зависимости (14) площади контакта А для нормальной нагрузки N = 500 К соответствуют приблизительно соотношению А_г = 0,1 % А

Тогда формулы для расчёта мощности объёмных источников тепла Томсона с учётом вы шеизложенного примут вид: для инструментального материала

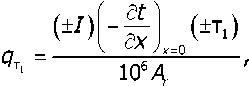
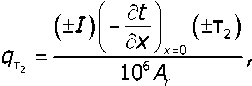
для материала контртела где I— ток, A; df / Эх— градиент, °С/м; т,— коэффициенты Томсона, мкВ/°С; А — фактическая площадь контакта, м2; 106 — переводной коэффициент. Комбинация знаков при трёх сомножителях выражений (15) и (16) (их алгебраическое произведение) даёт знак при источниках q и q^, что и определяет их тепловой эффект (табл. 1). Значения температурных градиентов следует принимать из решения контактной тепловой задачи.

В табл. 2 приведены исходные данные и результаты расчёта мощностей объёмных источников по (15), (16) и в пластине из сплава Т15К6, и в заготовке из Ст35 соответственно для скорости трения 1/ = 3,5 м/с.

Таблица 2

Мощность объёмных источников тепла Томсона для пары твёрдый сплав Т15К6 — Ст35

Скорость трения V, м/с	Мощность трения q, МВт/м2	Температура поверхности Тп, °C	Коэффициент Томсона, 10"6 В/°С		Температурный градиент, 10"6 °С/м		Мощность объёмных источников, МВт/м3
			Т1	т2	971 / Эх	ЭТ2 / Эх	<7п	»2
2,0	255	712	0	-3,5	0,91	5,81	0,0	103,9
3,0	383	872	+9	-9,0	0,99	8,87	45,6	408,1
3,5	448	942	+16	-13,0	1,06	10,29	86,7	684,7

Аналогичным образом по (14) рассчитывались мощности объёмных источников тепла Томсона в пластинах и заготовках для твёрдых сплавов Т15К6, ВК8; быстрорежущей стали Р6М5 и

Ст35, 1Х18Н9Т и ВТЗ-1 в широком диапазоне изменения скоростей трения. Для твердосплавных материалов максимальная сила тока, подаваемого через зону трения, выбиралась равной ± 8 А, для быстрорежущей стали — ± 4 А. Эти значения соответствуют предельным значениям триботока, протекающего через контакт [22]. Результаты приведены на рис. 4. Как следует из полученных данных, тепловое действие источника Томсона в пластинах инструментального материала может быть различным даже при одном направлении тока, что связано с температурной зависимостью величины и знака коэффициента Томсона (рис. 2).

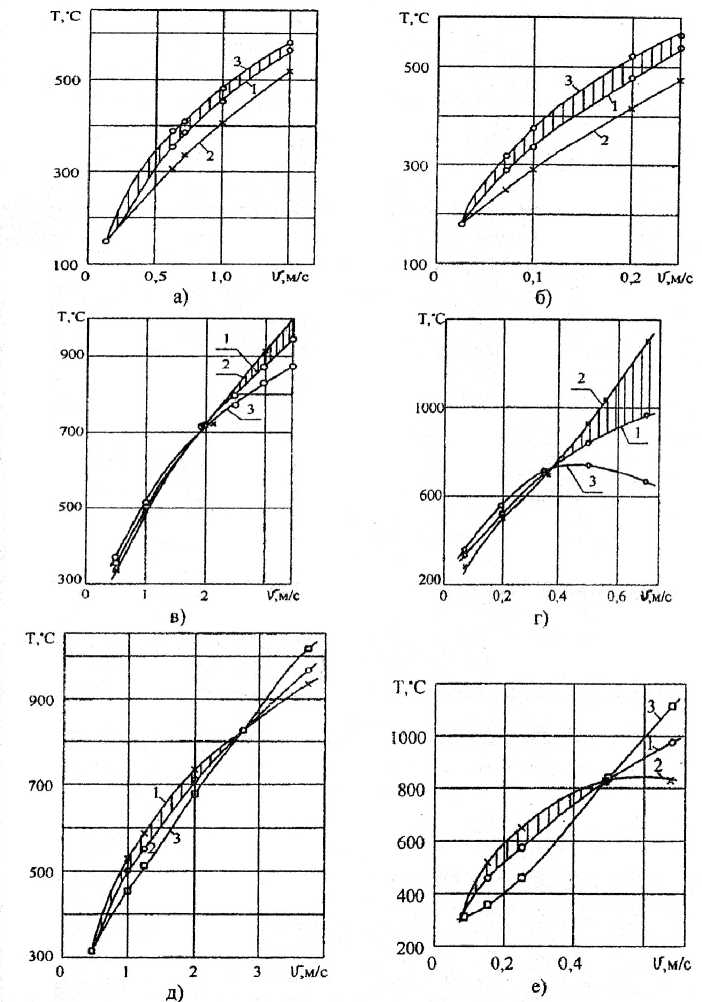
Рис. 4. Влияние токового режима на поверхностную температуру для следующих пар трения:

а — Р6М5 — Ст35, б — Р6М5 — ВТЗ-1: 1 — 1 = 0, 2 — 1= -4 А, 3 — 1= +4 А;

в — Т15К6 — Ст35, г — Т15К6 — ВТЗ-1, д — ВК8 — Ст35, е — ВК8 — ВТЗ-1: 1 — 2=0, 2 — 2 = -8 А, 3 — 2 = +8 А

При трении и резании большинства конструкционных материалов быстрорежущая сталь является положительным полюсом в цепи естественной термопары, устранение циркуляции есте- ственного триботока через зону контакта будет способствовать его охлаждению (заштрихованная область на рис. 4, а, б). Это относится и к твёрдым сплавам, только охлаждающий эффект контактной зоны в определённом диапазоне скоростей соответствует отрицательному направлению тока. Для твёрдых сплавов, независимо от материала контртела, существует область скоростей трения, где устранение циркуляции естественно возникающего триботока через контакт снижает его температуру (заштрихованная область на рис. 4, в, г, д, е). За критическим значением скорости трения, соответствующей температуре изменения знака коэффициента Томсона Ti (700 °C для Т15К6 и 840 °C для ВК8), естественный триботок будет охлаждать контакт (для ВК8) или нагревать его (для Т15К6). Полученные данные находятся в полном соответствии с характером изменения знака коэффициента Томсона у инструментальных материалов при вариации температуры и действием объёмного источника тепла Томсона в пластине инструментального материала.

Влияние токового режима пары трения на характер распределения температур по нормали к ПО'

верхности трения пластин инструментальных материалов по результатам расчёта на ЭВМ приведено на рис. 5—7. Независимо от материала пластин охлаждающее действие тока приводит к увеличению температурных градиентов, снижению зоны максимального прогрева △, т. е. локали зации зоны Л к поверхности контакта, падению температуры контакта.

Для быстрорежущей стали Р6М5 в диапазоне реальных скоростей трения нагревающее действие производит положительный постоянный ток и естественный триботок (рис. 5), поэтому электроизоляция должна быть эффективна во всём диапазоне скоростей. У твёрдого сплава Т15К6 при скоростях более 2 м/с наблюдается аналогичная картина (рис. 6).

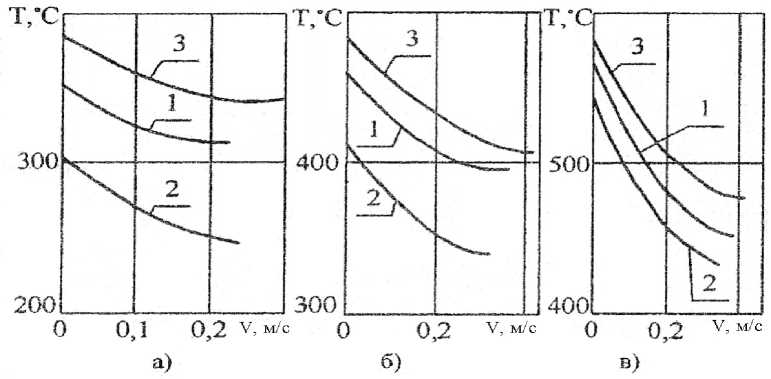
Рис. 5. Влияние направления постоянного тока на распределение температур по нормали к поверхности пластины из Р6М5 при трении по Ст35: а — I/ = 0,6 м/с, б — 1/= 1,0 м/с, в — 1/= 1,5 м/с: 1 — 1= 0, 2 — / = -4 А, 3 — 1= +4 А

При 1/= 2 м/с (Г,, ~ 700 °C) коэффициент Томсона для Т15К6 равен нулю и тепловое действие тока не проявляется. С переменой знака коэффициента Томсона у твёрдого сплава при одном направлении тока меняется и его тепловое действие. Это обстоятельство отчётливо проявляется для пары ВК8 — Ст35. При 1/= 1 м/с (7^ ~ 500 °C) коэффициент Томсона ВК8 (рис. 2) имеет практически максимальное положительное значение и отрицательный ток (естественный триботок) дополнительно нагревает объём материала (кривые 1 и 3, рис. 7, а). При трении с 1/= 3,75 м/с (Т_п ~ 980 °C) т_х имеет отрицательную величину, и отрицательный ток в этом случае проявляет охлаждающее действие (рис. 7, б).

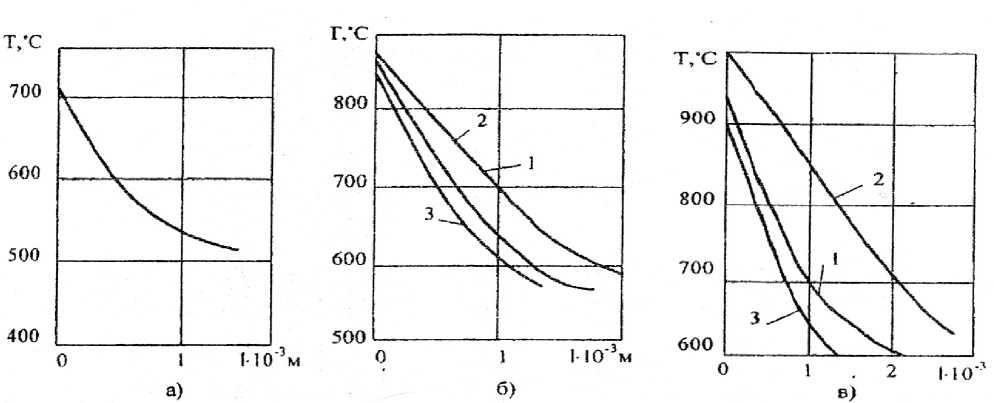
Рис. 6. Влияние направления постоянного тока на распределение температур по нормали к поверхности трения сплава Т15К6 (пара Т15К6 — Ст35): а — 1/ = 2,0 м/с; б — У = 3,0 м/с, в — У= 3,5 м/с: 1 — 1=0, 2 — 7= -8 А, 3 — 7= +8 А

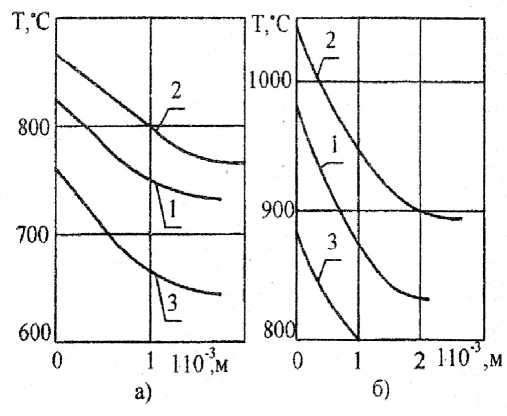
Рис. 7. Влияние направления постоянного тока на распределение температур по нормали к поверхности трения сплава: а, б — пара ВК8 — СтЗ: а — 1/= 1,0 м/с, б — I/ = 3,75 м/с; в, г — Т15К6 по титановому сплаву ВТЗ-1: в — V = 0,5 м/с, г —

V= 0,7 м/с: 1 — 7=0, 2 — 1= -8 А, 3 — 1= +8 А

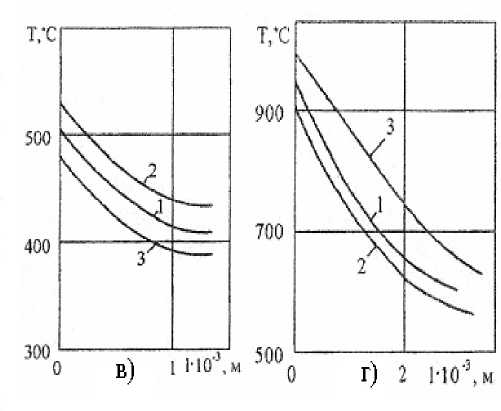
В условиях трения в паре с малотеплопроводными материалами 1Х18Н9Т и ВТЗ-1 механизм теплового действия тока в принципе не изменяется (рис. 6 и 7, в, г), однако увеличивается разница в температурах (контакта и на глубине) в зависимости от направления тока и обычных условий (1 = 0), что связано с большими, чем для Ст35, величинами температурных градиентов. Заключение. В зависимости от теплового действия тока изменяется и доля теплового потока, поступающего в пластину. Если пластина дополнительно охлаждается теплом Томсона, в ней повышаются температурные градиенты, и из-за этого несколько возрастает тепловой поток (1 - о)д в пластину (1 - о)<7 = о ЭЛ (х) / Эх. Так, по приведённым выше расчётам для пары Т15К6 — 1Х18Н9Т: при 1 = 0 величина (1 - a)q = 5,74 МВт/м²;

при 1= -8 А (нагрев) (1 - a)q = 3,9 МВт/м²;

при 1= +8 А (охлаждение) (1 - a)q = 6,97 МВт/м².

Таким образом, нагревающий объёмный источник в пластине выполняет роль своеобразного теплового «подпора», способствующего уменьшению доли суммарного потока тепла, поступающего в пластину, расширению зоны прогрева пластины и падению grad Т. Охлаждающий объёмный источник в пластине инструментального материала, наоборот, отводит из зоны контакта дополнительное количество тепла, увеличивая температурный градиент и сужая зону прогрева.

Статья подготовлена в ходе работ по государственному контракту на выполнение научноисследовательских работ с Минобрнауки России от 29 апреля 2011 года № 16.552.11.7027.