Трёхмерная контактная задача о взаимодействии упругого клина с двумя штампами при учёте трения
Автор: Пожарский Дмитрий Александрович, Поляков Анатолий Сергеевич
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Физико-математические науки
Статья в выпуске: 7 (68) т.12, 2012 года.
Бесплатный доступ
В квазистатической постановке изучена пространственная контактная задача для упругого клина, в одну грань которого симметрично вдавливаются два одинаковых эллиптических в плане жёстких штампа с учётом трения. Другая грань клина свободна от напряжений. Область контакта считается неизвестной. Рассмотрены случаи движения штампов перпендикулярно ребру клина. При этом штампы могут приближаться к ребру или удаляться от него. При использовании известной функции Грина для трёхмерного клина контактная задача сведена к интегральному уравнению (ИУ) относительно контактного давления. Для решения ИУ применяется метод Галанова, позволяющий одновременно определить область контакта и давление в этой области. Сделаны расчёты при разных коэффициентах трения, углах раствора клина и расстояниях между штампами.
Теория упругости, контактная задача, клин, трение, метод галанова
Короткий адрес: https://sciup.org/14249917
IDR: 14249917 | УДК: 539.3
Текст научной статьи Трёхмерная контактная задача о взаимодействии упругого клина с двумя штампами при учёте трения
Введение. Исследована задача о квазистатическом контакте с трением двух симметрично расположенных штампов на грани трёхмерного упругого клина. Другая грань клина свободна от напряжений. Штампы начинают медленно двигаться перпендикулярно ребру клина. Симметричные области контакта неизвестны. Для решения использован метод нелинейных граничных ИУ [1, 2]. Ранее исследовались аналогичные задачи для одного штампа без учёта трения [1] и с учётом трения [3]. Изучалось взаимодействие двух штампов без учёта трения [4, 5].
Постановка задачи. Рассмотрим в квазистатической постановке трёхмерную контактную задачу для упругого клина {ге [0, оо]; ф е [-о, о]; ze (-оо, оо)} с учётом сил трения, действующих перпендикулярно ребру клина, когда грань клина ф = -о свободна от напряжений. Пусть два симметричных жёстких штампа, первоначально внедрённых в грань ф = о, начинают достаточно медленно двигаться по этой грани (без перекоса) перпендикулярно ребру клина. Упругие параметры материала клина — G (модуль сдвига) и v (коэффициент Пуассона). Силы трения коллинеарны направлению движения (и направлены против движения). Штампы имеют форму эллиптических параболоидов, их подошвы описываются функциями
Задача симметрична относительно полуоси г. На штампы действуют нормальные вдавливающие силы Р, имеющие плечи ^(относительно полуоси г) и ^(относительно ребра клина), и касательные силы Т, направленные перпендикулярно ребру клина. В соответствии с законом Кулона выполняется соотношение Т = рР, где р — коэффициент трения Кулона. Условие контакта штампов и клина имеет вид u^r,a,z) = -\5-f±(r,z^, (r,z)eQ±,
где u^r, о, z) — нормальное перемещение упругого материала клина с одной свободной от напряжений гранью при действии на другой грани нормальных и касательных напряжений, м;
б — осадка штампов, м; Q+ — неизвестные области контакта, м2. Смена знака р эквивалентна изменению направления движения штампа на противоположное. Трением вдоль ребра клина пренебрегаем.
При известных величинах о, р, G, v, б и заданных функциях f(r, z) требуется определить нормальное контактное давление о^г, о, z) = -q^r, z), (г, z) е Q+, найти области контакта О±, а также значения Р, Hrv\ Hz.
Решение задачи. При помощи условия контакта (2) выводится ИУ относительно функции q^r, z) в неизвестной области Q+. Решив это уравнение и определив q^r, z) и Q+, можем найти величины Р, Hrv\ Hzv\3 условий равновесия штампа. Для вывода ИУ рассмотрим две вспомогательные краевые задачи. Граничные условия первой имеют вид:
Ф = а: ор = -Q16(r-x)6(z-y), тГ(р = тр2 = 0 ; (3)
Ф = -а:
^ = T«p = Tpz = 0.
Здесь 6W — дельта-функция Дирака. Решение задачи (3), (4) известно [1]. Используя его, найдём
2Q
о о
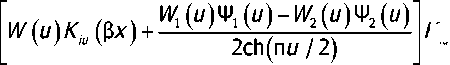
6 =^/(1- v),
Kiu^ cos p(z- у) dud$,
... / x sh4au +sin4a ...
И/ ( и) =--------------55--------, W.
v ’ ch4au -2u sin2 2a-1 '
ch2au + cos2a
-sh2au ± u sin2a'
где функции Ф^ц) (л = 1,2) удовлетворяют ИУ Фредгольма второго рода:
О
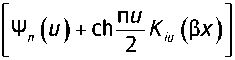
. / \ I FIT । \ f
£я(т,(у) = 2сМ—sh —И/(y)J Z Z 0
/ x _ cthaf sin2 2a ^ ' ch2af - cos 4a '
shnf дп (t^dt
(chnf +chnT)(chnf +chnu) ' / x _ thaf sin2 2a
^2 ' ch2af +cos 4a "
С использованием известного интеграла [1] выделим в формуле (5) главную часть, соответствующую упругому полупространству:
jshnty K™ (P^)^(")-cthnt/)^ (px)
Iv/X I I О Q Q
(Ю)
2ch(nu /2)
cosp(z -y)dud$,
R =
(И)
Граничные условия второй вспомогательной краевой задачи имеют вид: Ф = а: ар=тр2=0, тгр =Q26(r-x)6(z-y);
Ф = -а: оф = тгр = тр2 = 0.
Решение задачи (12), (13) также известно [3]. Используя его, найдём
co co
"Ф (r'a'z) = Jcosp(z - y)shn^/u (pr) Kiu (Px)fo (u) + п У о o
2ch(nu /2)
dud^
Q2 n392(l-v)
JcosP(z -y^pJJ^ ^hx (f) -И/2 (у)Л2 (t)]shnu shnf
0 0
2u sin2 2a ch4au — 2t/2 sin2 2a-1'
chnf -chny
, . . (1 — 2v)sh2a t/+1/sin 2a А1 2 (У) = ------э------ ' v ’ ch2au + cos2a
Здесь функции Ф* (и) (л = 1,2) удовлетворяют ИУ Фредгольма второго рода о L J
’n \U)Kiu (P%) 1 Г Пп У)Ка (p%) h tdt
2(l-v)(l-2v) 2(l-v)j chnf-chnu '
. / x ±u 2(1-v)(l-2v)sin2a
1,2v ' IV12(t/) ch2au + cos2a
Используя значение интеграла 4 г г chntchnu-1 „ X... г-х
rfWy-yy»^ К- W-
I I Q Q Q L I I I I L L I I I I iV TN выделим в (14) главную часть, соответствующую упругому полупространству: ^!!cosP(z -K|shnu K-(Pr| *
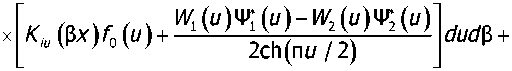
n302(l-v)
j cos P (z - у )УР j j ^И^ (u) hx (t ) - И/2 (u) /?2 (t )] sh n u sh n t 0 0 0
-2 (1 - 2v)(ch n u ch nf -1)1
' Л '’ chnt-chnu
В соответствии с принципом суперпозиции заменим в (5) силу Qi на искомое давление ф<, у), а силу Qz в (20) — на распределённые силы трения т(х, у) = pq(x, у). Проинтегрировав далее правые части полученных соотношений по области контакта Q+ и Q по переменным х, у и сложив их, получим при помощи условия контакта следующее ИУ:
jj q(x,y)L_ (x,y,r,z^dxdy = d± (r,z), (r,z)eQ+uQ_,(21)
где
L±(x,y,r,z^ = l^ (x,y,r,z) + pLl(x,y,r,z), d±(r,z) = 2n6^5 - f±(r,z)^,(22)
14 r r
11 о 0
2ch(nu / 2)
cos₽(z +y)dud^>,
1 - 2v r -
2(l-v)' R
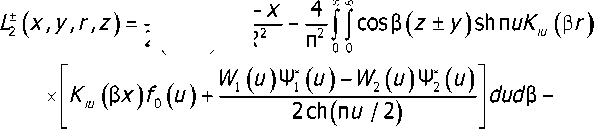
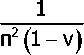
j cos 3 (z ± у) a -2 (1 - 2v)(ch nu ch nf -1)1 Kiu^,r^Kit^lX^ dtdu ' Л ’’ chnf-chnt; В силу симметрии ИУ (21) сводится к уравнению JJq (x,y)|^£ (x,y,r,z) + L+ ^x,y,r,z5\dxdy = d ^r,zy ^r,z) e Q_. Q (25) Введём новые обозначения: z,=z-h, y,=y-h, q,(r,z,) = q(r,z), QoQ_. (26) Перепишем уравнение (25) в форме JJV (х,у,)Цх,у,,r,z,)dxdy, =d(r,z,y (r,zt)eQ , (27) t/(r,z) = 2nef5-^-a^ - — , v 7 2R 2R. (28) К (x,y,r,z) = L (x,y,r,z) + £+ (x,y + h,r,z + h). (29) Звёздочки далее опускаем. Для решения ИУ (27) при условии q(r,z) = 0, (r,z) е Q используем метод нелинейных граничных ИУ типа Гаммерштейна [1, 2], позволяющий одновременно определить область контакта, контактное давление и нормальное перемещение упругого материала вне области контакта. Введём обозначения М = ^r,zy N =^х,у^ и предположим, что область контакта целиком содержится в прямоугольнике S = {|r-а| b>c, который не выходит на ребро клина. Уравнение (27) дополним условием неотрицательности контактного давления в области контакта, а также условиями отсутствия контакта и обращения в нуль давления в дополнительной области S \ Q, записав их все в виде системы: ^K(N,M)q(N)dN = d{M), q^>0, М е Q, ■(30) Ls Введём нелинейные операторы p(M) = sup{p(M),0[, p (M) = inf{p(M),0[.(31) Идея метода заключается в представлении искомого давления в форме q=q(M) = q (M) + q (М)( с целью автоматического удовлетворения интегрального неравенства (33) в ходе решения нелинейного операторного уравнения типа Гаммерштейна где р= р(М), /7 = р(М), d= d^M), Кр+ =jK(N,M)p+(N)dN.(34) s Эквивалентность системы (30) и уравнения (33) устанавливается в теореме, аналогичной известным теоремам [1, 2]. При численном решении уравнения (33) применим модифицированный метод Ньютона [1]. Введём следующие безразмерные обозначения: r-a = r'b, x-a = x'b, z = z'b, y = y'b, 5 = 5’Ь, A = b/(2R1), В = Ь!^\ К = а]Ь, к = Ь]Ь, г = с!Ь, q'V'.z'VqV-zW^, Р' = Р/(2п9Ь2у S'^S, Q'^Q, Штрихи далее опускаем. Параметр Л характеризует близость областей контакта к ребру клина, параметр к характеризует удалённость штампов друг от друга. В расчётах полагали й = А = В=г = Х,м = 0,5. В таблице даны значения вдавливающей силы Рдля разных углов клина 2о при изменяющихся значениях Л, к и ц. При движении штампа к ребру клина (р<0) сила меньше, чем для случая удаления от ребра (р>0). С уменьшением значения Л или угла клина величина Р падает. Эти факты объясняются приближением областей контакта к грани, где отсутствуют напряжения. Известно [3], что вдали от ребра клина величина /^б) практически не зависит от коэффициента трения ц. Вблизи ребра клина это уже не так. Чем больше осадка, тем больше сила. Большая вдавливающая сила требуется при удалении штампов друг от друга (параметр к возрастает). Значение к = оо соответствует случаю одного штампа. Взаимовлияние штампов существенно проявляется при уменьшении параметра к (36). Значения вдавливающей силы Р к м 1,2 2 з 1,2 2 з 2а = 60°; Л = 1,2 2а = 60°; Л = 2 0,2 0,071 0,079 0,083 0,102 0,092 0,098 0,105 0,134 0 0,064 0,070 0,075 0,092 0,082 0,089 0,096 0,123 -0,2 0,058 0,065 0,069 0,084 0,076 0,082 0,088 0,113 2а = 90°; Л = 1,2 2а = 90°; Л = 2 0,2 0,172 0,185 0,195 0,221 0,193 0,206 0,215 0,244 0 0,157 0,170 0,180 0,205 0,179 0,192 0,202 0,233 -0,2 0,145 0,157 0,166 0,191 0,168 0,180 0,190 0,222 Заключение. Решена новая пространственная контактная задача с неизвестной областью контакта для упругого клина о взаимодействии двух одинаковых эллиптических в плане штампов с учётом трения при одной свободной от напряжения грани клина. При использовании метода нелинейных граничных ИУ с учётом симметрии задач определены области контакта, давления в этих областях, вдавливающие силы. Сделаны расчёты при разных значениях угла раствора клина и коэффициента трения. Работа поддержана грантами РФФИ 12-01-00065,12-01-00991.
Список литературы Трёхмерная контактная задача о взаимодействии упругого клина с двумя штампами при учёте трения
- Александров, В. М. Неклассические пространственные задачи механики контактных взаимодействий упругих тел/В. М. Александров, Д. А. Пожарский. -Москва: Факториал, 1998. -288 с.
- Галанов, Б. А. Метод граничных уравнений типа Гаммерштейна для контактных задач теории упругости в случае неизвестных областей контакта/Б. А. Галанов//Прикладная математика и механика. -1985. -Т. 49, вып. 5. -С. 827-835.
- Пожарский, Д. А. О трёхмерной контактной задаче для упругого клина при учёте сил трения/Д. А. Пожарский//Прикладная математика и механика. -2000. -Т. 64, вып. 1.-С. 151-159.
- Молчанов, А. А. Взаимодействие штампов на грани упругого клина/А. А. Молчанов, Д. А. Пожарский//Прикладная математика и механика. -2010. -Т. 74, вып. 4. -С. 681-690.
- Соболь, Б. В. Пространственная задача о контакте системы штампов с упругим слоем/Б. В. Соболь, И. М. Пешхоев//Экологический вестник научных центров ЧЭС. -2011. -№ 1. -С. 69-76.


