Трёхуровневая модель, основанная на физических теориях пластичности: формулировка, алгоритмы реализации, результаты применения для исследования циклического нагружения
Автор: Трусов Птр Валентинович, Грибов Дмитрий Сергеевич
Журнал: Вычислительная механика сплошных сред @journal-icmm
Статья в выпуске: 3 т.15, 2022 года.
Бесплатный доступ
Хорошо известно, что физико-механические свойства металлов и сплавов и эксплуатационные характеристики изделий из них в значительной степени определяются мезо- и микроструктурой материалов. В связи с этим в последние десятилетия для исследования технологических процессов термомеханической обработки металлов и сплавов интенсивно развиваются и всё более широко применяются физически-ориентированные модели, позволяющие анализировать эволюцию структуры материалов. Указанные модели основываются на введении внутренних переменных, физических теориях пластичности (упруговязкопластичности) и многоуровневом подходе. В работе рассматриваются структура, математическая формулировка и алгоритм реализации трёхуровневой (макро-, мезо-1 и мезо-2 уровни) дислокационно-ориентированной модели, предназначенной для исследования поведения представительного макрообъёма (макрообразца) моно- и поликристаллических сплавов при произвольных траекториях деформации. Нагружение осуществляется кинематически, для связи макро- и мезоуровня-1 используется гипотеза Фойгта (Тейлора). Подмодель мезоуровня-2 оперирует с плотностями и скоростями движения полных и расщеплённых краевых дислокаций на системах скольжения; учитываются взаимодействия дислокаций различных систем: аннигиляция, упрочнение за счёт дислокаций леса, формирование барьеров дислокационной природы (Ломера-Коттрелла, Хирта). На мезоуровне-1 описание выполняется в терминах касательных напряжений и скоростей сдвигов по системам скольжения, устанавливаемым с помощью уравнения Орована по данным, получаемым с мезоуровня-1. Для учёта ротации кристаллитов вводится жёсткая подвижная система координат, связанная с кристаллической решёткой. Отклик материала на макроуровне определяется путём осреднения напряжений в кристаллитах. Представляются результаты приложения сформулированной модели к исследованию деформирования макрообразцов из сплавов с различной величиной энергии дефекта упаковки по простым и сложным замкнутым траекториям деформации. Показано, что материалы с низкой энергией дефекта упаковки демонстрируют эффект дополнительного циклического упрочнения при нагружении по сложным траекториям деформации.
Трёхуровневая дислокационно-ориентированная модель для исследования поведения моно- и поликристаллов, простое и сложное циклическое нагружение, эффект дополнительного циклического упрочнения
Короткий адрес: https://sciup.org/143179339
IDR: 143179339 | УДК: 539.3 | DOI: 10.7242/1999-6691/2022.15.3.21
Текст научной статьи Трёхуровневая модель, основанная на физических теориях пластичности: формулировка, алгоритмы реализации, результаты применения для исследования циклического нагружения
Одна из насущных задач конструкторов, технологов, материаловедов, механиков в течение многих десятилетий — снижение материалоемкости изделий при одновременном повышении их эксплуатационных свойств. Широко распространенными конструкционными материалами являются металлы и сплавы в поликристаллическом состоянии. Известно, что физико-механические свойства сплавов и рабочие характеристики изделий из них определяются не только химическим составом, но в большинстве случаев, что даже более существенно, микро- и мезоструктурой [1–4], формирующейся и эволюционирующей в процессе термомеханической обработки при изготовлении. Следует отметить, что в настоящее время технологические режимы обработки материалов, как правило, основываются на предварительном математическом моделировании протекающих при этом процессов. Важнейшей составляющей необходимого для моделирования «инструментария» служат конститутивные модели (или определяющие соотношения (ОС)), описывающие поведение материалов.
Моделирование, предшествующее внедрению технологических процессов переработки материалов в практику, активно развивается со второй половины ХХ века. Первоначально в его основу полагаются макрофеноменологические теории пластичности [5–9]. Созданные в их рамках модели отличаются относительно простыми математическими формулировками и алгоритмами реализации при построении численных процедур решения краевых задач нелинейной механики деформируемого твердого тела, однако требуют существенных временных и материальных затрат для экспериментальной идентификации; кроме того, в указанных теориях отсутствует возможность учета структуры материалов. Затруднения возникают и при построении ОС для сложных нагружений [10–12].
Указанные недостатки макрофеноменологических теорий обусловили поиски новых подходов к построению ОС; в последние десятилетия получили развитие конститутивные модели, основанные на введении внутренних переменных [13–18], физических теориях пластичности и многоуровневом подходе [19–25], позволяющие описывать эволюционирующую в процессах термомеханической обработки микро- и мезоструктуру материалов. Эти физически-ориентированные модели представляются авторам наиболее перспективными по следующим причинам: их формулировка в явном виде включает наиболее значимые физические механизмы и их «носители» на различных структурно-масштабных уровнях, также связи между ними; они обладают значительной универсальностью в силу схожести физических процессов на нижних структурно-масштабных уровнях для целых классов материалов; при условии многоуровневости нет необходимости классифицировать процессы нагружения по их типу, изменять форму записи ОС; физически-ориентированные модели используют результаты натурных экспериментов, однако главным образом для установления материальных параметров, входящих в их ОС, при этом структура модели и ее уравнения сохраняют неизменный вид. К сложностям применения таких моделей можно отнести значительные вычислительные затраты, обусловленные как большим количеством искомых переменных на разных структурно-масштабных уровнях, так и необходимостью определения многочисленных параметров, входящих в соотношения, описывающие процессы эволюции структуры на каждом уровне. Данная задача разрешается использованием подмоделей более глубоких масштабных уровней, например, подмоделей дислокационной или молекулярной динамики [26].
В технологических операциях обработки давлением металлы испытывают, как правило, нагружение по сложным траекториям деформации, в том числе циклическим; например, на завершающей стадии изделия могут подвергаться обкатке роликами, дробеструйной обработке, знакопеременному изгибу (рихтовке). В таких процессах реализуется множественное скольжение дислокаций по разным системам скольжения (СС); при взаимодействии дислокаций разных СС в ряде сплавов формируются барьеры дислокационной природы (Ломера–Коттрелла, Хирта), обусловливающие дополнительное упрочнение за счёт сложного нагружения [27–34]. Известно, что склонность металлов и сплавов к образованию барьеров дислокационной природы в значительной степени зависит от величины энергии дефекта упаковки (ДУ) [35–37]. Сложное на макроуровне нагружение приводит к множественному скольжению по СС кристаллитов, что увеличивает вероятность реакции расщеплённых дислокаций с образованием указанных барьеров. Связь типа нагружения и величины дополнительного упрочнения подтверждают работы [38, 39], в которых приведены результаты экспериментов для плоских квадратных траекторий деформации в двумерном подпространстве совмещённого пространства напряжений–деформаций. Показано, что деформационное упрочнение при несинфазных (непропорциональных) циклах значительно превышает упрочнение при простых циклических нагружениях. Для теоретического анализа использована теория течения с комбинированным изотропно-кинематическим упрочнением, результаты расчётов обнаруживают качественное соответствие экспериментальным данным.
В [40] представлена информация об экспериментах на сложное (непропорциональное) нагружение, проведённых на тонкостенных трубчатых образцах из сталей 304 и 316; отмечается значительное увеличение напряжения течения при непропорциональном нагружении по сравнению с простым; предложена классификация процессов упрочнения в зависимости от сложности нагружения. В работах [41, 42] обсуждаются результаты экспериментов на пропорциональное и непропорциональное циклические нагружения образцов из меди, алюминия и нержавеющих сталей. При исследовании микроструктуры образцов из меди и сталей авторы обнаружили образование относительно простых дислокационных субструктур (стенок дислокаций, сеток) при простом нагружении и формирование сложных ячеек и петель при сложном нагружении. Как выяснилось, для сталей и меди величина дополнительного циклического упрочнения достигает 50%, что объясняется низкой энергией ДУ. Предложена модификация закона эволюции поверхности текучести при различных типах нагружения, позволяющая в рамках теории пластического течения описать сложное циклическое деформирование.
Работа [43] содержит обзор экспериментов по определению отклика металлов на циклическое деформирование в зависимости от энергии ДУ и показано, что в материалах с её высоким уровнем дополнительное циклическое упрочнение при сложном (непропорциональном) нагружении отсутствует. Предложено соотношение связи уровней упрочнения при монотонном и циклическом нагружениях. В [44] приведены результаты исследования сложного циклического нагружения по двумерным траекториям деформации (в совмещённом пространстве напряжений–деформаций) тонкостенных трубчатых образцов из суперсплава на никелевой основе. За меру непропорциональности F авторы принимают отношение длин минимальной и максимальной осей эллипса, охватывающего исследуемую траекторию деформации. Отмечается, что дополнительное циклическое упрочнение не наблюдается при малых деформациях и значениях фактора F < 0,4.
Феноменологическая модель, представленная в [45], позволяет учитывать зависимость тензора напряжений от деформаций при многоосном пропорциональном и непропорциональном циклических нагружениях. Принимается, что поверхность текучести испытывает изменения формы и повороты в процессе пластического деформирования; для непропорционального циклического нагружения получена простая зависимость между компонентами тензоров напряжений и деформаций. Результаты расчётов с использованием модели удовлетворительно согласуются с экспериментальными данными. Детальному описанию феноменологической модели, включающей историю деформирования, и результатам её применения в случае сложного циклического деформирования посвящена статья [46]. Экспериментальные исследования образцов из алюминиевого сплава при широком спектре многоосных нагружений дали возможность определить параметры модели и осуществить ряд вычислительных экспериментов. Авторы отмечают хорошее соответствие численных результатов экспериментальным данным, как качественное, так и количественное.
Важно, что макрофеноменологические ОС, сформулированные для описания процессов непропорционального нагружения, значительно отличаются своими формулировками, поскольку их приходится приспосабливать к исследуемым материалам и программам нагружения. Выше говорится, что наряду с ними активно развиваются многоуровневые физически-ориентированные модели. Именно они в последние 10 лет находят всё более широкое применение. Многоуровневые модели включают явное описание эволюции дислокационных и других дефектных субструктур [47–49], а также механизмов пластического деформирования и их носителей (сдвигов по СС, скольжения краевых дислокаций, двойникование и другого), что позволяет построить, в частности, физически обоснованные законы упрочнения [50, 51]. В настоящей работе используется дислокационно-ориентированный подход к построению моделей, основанный на введении внутренних переменных, разделённых на явные и неявные [ 4, 25 ] . Явные переменные входят в структуру ОС каждого масштабного уровня, неявные переменные характеризуют более низкие по масштабам микроструктуры.
-
2. Структура и основные соотношения модели
Разработанная модель относится к классу трёхуровневых; для описания деформирования поликристаллического образца рассматриваются следующие структурно-масштабные уровни:
макроуровень, мезоуровень-1 и мезоуровень-2. Ключевым механизмом неупругого деформирования в данной работе полагается движение краевых дислокаций. На мезоуровне-2 механизм неупругого деформирования выражается через плотности и скорости движения дислокаций на СС этого уровня. На мезоуровне-1 неупругое деформирование представляется в терминах скоростей сдвигов по кристаллографическим СС, которые определяются с помощью уравнения Орована по параметрам, установленным на мезоуровне-2. Для связи уровней в конститутивные соотношения каждого из уровней вводятся явные и неявные внутренние переменные [25], следующие из замыкающих уравнений,
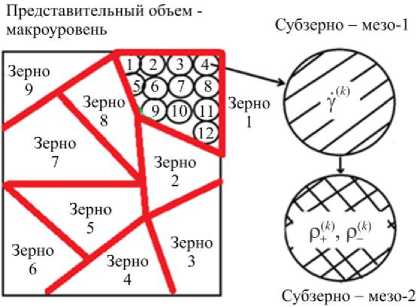
Рис. 1. Структура модели: представительный объём поликристаллического материала, зерно, субзерно, их связи и иерархия
моделирующих процессы деформирования на более глубоких уровнях.
Представительный объём макроуровня включает в себя набор зёрен. Зёрна содержат статистически значимое множество (десятки и сотни) кристаллитов (субзёрен, фрагментов, для которых с принятой точностью можно считать одинаковой ориентацию решётки, а внутренние переменные — однородными). Эти элементы принадлежат мезоуровню-1 и имеют в отсчётной конфигурации в пределах каждого зерна небольшие (порядка нескольких градусов) случайные отклонения ориентаций (Рис. 1). С элементами мезоуровня-1 масштабно совпадают элементы мезоуровня-2. На макро- и на мезоуровне-1 описание ведётся в терминах механических переменных (в напряжениях, деформациях и их скоростях), на мезо-2 модель оперирует с плотностями различных дефектов на каждой СС. Нагружение на макроуровне задается законом предписанного изменения во времени градиента скорости перемещений. В качестве воздействия на мезоуровень-1 с макроуровня передаются температура и кинематические переменные, используется гипотеза Фойгта (равенство градиентов скорости перемещений на уровнях макро и мезо-1). На мезоуровне-1 рассматриваются касательные напряжения и скорости сдвигов по его СС. Полученные на СС мезоуровня-1 касательные напряжения играют роль внешних воздействий на мезоуровень-2, где определяются эволюция плотностей дефектов и упрочнение по СС мезо-2. Найденные согласно уравнению Орована на мезоуровне-2 скорости сдвигов по СС сообщаются мезоуровню-1.
В подмодели мезоуровня-2 применяется разделение плотностей дислокаций по СС на положительные и отрицательные (в зависимости от направления экстраплоскости). Внутренними переменными подмодели мезоуровня-2 являются: плотности дислокаций (положительных и отрицательных), плотности источников дислокаций на СС и образованных на них барьеров скольжению [52, 53]. Наибольшее внимание при построении предлагаемой модели уделяется физически обоснованному описанию дислокационного скольжения, взаимодействия дислокаций друг с другом, в том числе расщеплённых дислокаций с образованием барьеров Ломера-Коттрелла и Хирта.
Далее «родственные» характеристики макро- и мезоуровня-1 обозначаются одинаковыми буквами, прописными — на макроуровне, и строчными — на мезоуровне-1. Кинематическое воздействие, задаваемое на макроуровне с учётом гипотезы Фойгта (Тейлора) — Z = 7 V T , передается на мезоуровень-1 (номера элементов мезоуровня-1 опускаются):
z ( t ) = Z ( t ) = V V T , (1)
где 7 — оператор градиента (Гамильтона) в актуальной конфигурации, z — градиент скорости перемещений (мера скорости изменения деформации) в элементе мезоуровня-1.
На мезоуровне-1 с использованием пластической составляющей меры скорости деформации z in , определяемой по скоростям движения и плотностям дислокаций, найденным в подмодели мезоуровня -2, вычисляются компоненты тензора напряжений Коши о . Осреднение тензора о по совокупности кристаллитов, составляющих представительный объём макроуровня, позволяет установить тензор макронапряжений Коши L . По напряжениям о , единичным векторам нормали и направлениям скольжения находятся действующие на каждой к -й СС касательные напряжения т ( к ) мезоуровня-1. Скорости сдвигов у ( к ) вычисляются по скоростям движения и текущим плотностям дислокаций с мезоуровня-2. Эволюция внутренних переменных (мезоуровня-1 описывается следующей системой уравнений (номера элементов — кристаллитов, не приводятся) [ 25 ] :
О + о • w — го • о = п : ( z - to - z in ) , z = z е + z in ,
-
• T w = o • o , n
zin = £y< к) b(к) n( к), к=1
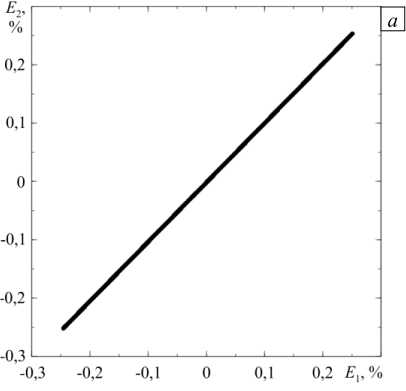
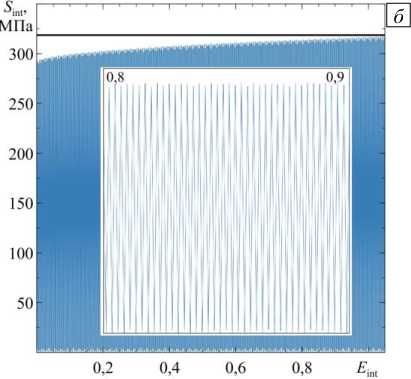
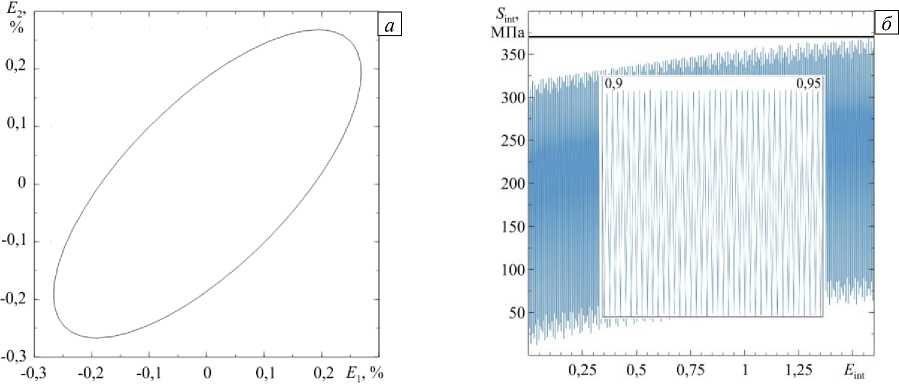
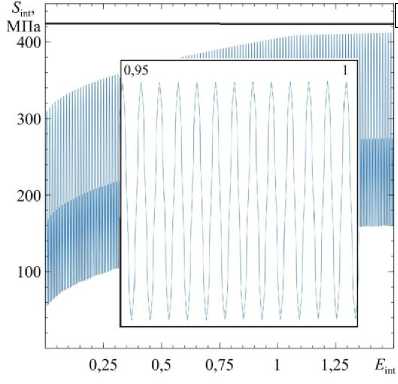
т(k) = b Описание эволюции дислокационной субструктуры производится на мезоуровне-2. В качестве воздействий с мезоуровня-1 на мезоуровень-2 передаются температура и действующие по СС касательные напряжения т(к). Эволюция плотностей дефектов на СС представляется с учётом наиболее значимых механизмов: зарождения дислокаций за счёт работы источников Франка-Рида; аннигиляции дислокаций разных знаков на одинаковых СС; изменения плотности барьеров на СС [20, 55]. На мезоуровне-2 также определяются средние скорости положительных и отрицательных дислокаций V±(к), зависящие от величины касательных напряжений т(к), температуры 0 , плотности положительных и отрицательных дислокаций р(+к), р(_к) и плотности барьеров р(2 на СС. Используется аддитивное разложение (к) на составляющие скорости изменения критических напряжений сдвига т^ в зависимости от изменений плотностей дислокаций по СС т(к\is и плотностей барьеров т(к\ог; в отсчётной естественной конфигурации критические напряжения вычисляются через сопротивление решётки т(к\аt . Скорости сдвигов находятся из уравнения Орована [56], записанного в скоростной форме. Система уравнений, отображающая поведение кристаллита на мезоуровне-2, имеет следующий общий вид [57, 58]: V/1 = ±fl 1< 1. т"Л 9, р”, р-')sign(т’к'), р"’ = f 2 (т--', тк, 9, р(к', р«) (к, l = ГК), < Г‘|=(р(' '^ >-р1- 1Г‘>) |ь(к’|, . f , (т--', * 9,р±', р™), , (к) = ,( -) тc 0 ± тс _ lat, t(к) =к) + ^(к) т c ± т c _ dis ± + т c _ bar ± , где |b(-)| — модуль вектора Бюргерса в к -й СС, K — число СС. При описании дислокационных реакций важнейшую роль играют средние скорости движения дислокаций противоположных знаков V(к), V(к), которые на одной и той же кристаллографической плоскости отличаются друг от друга не только знаком, но величиной. При этом необходимо учитывать, что движения дислокаций обоих знаков по одной СС вносят вклад в скорость сдвига по данной системе, в связи с чем потребовалась некоторая модификация уравнения Орована в скоростях [56]: Y(к) =(р(+кV(к )-р(_кМ-)) |b( к) I (4) Средние скорости движения дислокаций определяются из следующих соотношений [57, 58]: Vк) =1 (к)vexp(-АG*±-1вв9) H(|т(к)|-т^)) sign(т(к)), V-к) = -l(к)vexp(-АG.-±/-b9) H(|т(к)|-тСk?) sign(т(к)), A G.(±) = aF к) т(к) , 1 + gТ(- * тС ± l(к)=а , 1 nn . шр + "^ p(l 1 V i=1 i=1 Здесь: AF^(к), AGp) — зависящие от свойств решётки энергии активации движения дислокаций, соответственно, в отсутствие напряжений и при действии касательного напряжения на СС; кв — константа Больцмана; 9 — абсолютная температура; Н — функция Хэвисайда; l(к) — средняя длина свободного пробега дислокации к -й СС; v — дебаевская частота (максимальная частота, с которой могут колебаться атомы около своих положений равновесия); g, а, р, 5 — безразмерные параметры, определяемые из процедуры идентификации [58]. При изотермическом пластическом деформировании происходит образование новых дислокаций, в качестве их источников принимаются источники Франка-Рида, генерирующие замкнутые расширяющиеся петли дислокаций. Из экспериментов известно, что источник может испускать ограниченное число петель. В работе для описания генерации дислокаций вводится плотность источников Франка-Рида р(-с' м-3, изменение которой представляется следующим соотношением: рsk<)=Е £рЬаг*р(j)[ l(j)v exp (-aG*) /-в9) h (|т(у)| - тС;))], D (-) р0 src р0 src, где L — расстояние между препятствиями в источнике, р(-) — плотность барьеров на пересечении к -й и j -й СС (затрудняющая или препятствующая движению дислокаций по каждой из этих СС), р05ГС — начальная плотность барьеров. Вклад источника в увеличение плотностей дислокаций пропорционален текущей плотности петель и отличен от нуля только при активации источника. О её начале свидетельствует превышение действующими касательными напряжениями критических напряжений тчг [59]: , , /Iт(k)|V • (k) (к) /1 \ О ; — Г (У j----L —1 ) p nuc avp\ \ т src т src A^b ( 1L _ | = —— I ln — + B I. 2 nL ( r0 ) Здесь: rav — средний радиус петли; v — дебаевская частота; A , B , p — безразмерные параметры материала; p — модуль сдвига; г0 — минимальная длина закрепленного сегмента, способного генерировать дислокационные петли; b — величина вектора Бюргерса; (x) = xH (x) — оператор (скобки Маколея). Аннигиляция дислокаций происходит в результате реакции дислокаций с разными знаками в одной СС. Реакция возможна в случае, если две дислокации противоположных знаков оказались на малом расстоянии. Это явление играет большую роль в процессах деформирования, особенно при реверсивном нагружении. Дислокации разных знаков, принадлежащие одной СС, притягиваются; две дислокации разных знаков на параллельных СС могут переползать по направлению друг к другу и взаимоуничтожаться при сближении на расстояние h . Количество прореагировавших дислокаций в единицу времени пропорционально заметаемому дислокацией объёму (на единицу длины дислокации) и плотности дислокаций на СС. Для описания аннигиляции в работе предлагается использовать следующее соотношение [60]: P±k) ™ =- hmm Р(+ ^к )| V k)-V k )|. Для изображения зарождения и эволюции барьеров в настоящей работе авторами строится матрица плотностей барьеров Rk^, в которой единичные значения компонент стоят на пересечении строки к и столбца l , означающих номера СС, в которых залегают расщеплённые дислокации, реагирующие при пересечении с образованием барьеров Ломера–Коттрелла и/или Хирта; остальные компоненты матрицы Rkl нулевые. Скорость изменения плотности барьеров зависит на реагирующих системах от плотности дислокаций, действующих касательных напряжений и температуры [61]: Р L = VXd RL р(l )р(k) [ l(k) V exp (-AG*k) /кв б)], b b2G xd =------=------, 8Л8 sfe 8лу sfe где ψ — безразмерный параметр, характеризующий скорость образования барьеров для конкретного материала (определяется в процессе идентификации), x — средняя ширина расщепления дислокации, £sfe — безразмерная величина энергии ДУ (£SFE =уSFE/(Gb) , ysfe — энергия ДУ). Матрица плотностей барьеров на СС содержит данные обо всех барьерах, которые могут появиться на расщеплённых дислокациях (так для ГЦК решётки их 24) [58]. Компоненты матрицы ρkl описывают скорости изменения плотностей барьеров, возникших на пересечении дислокаций, принадлежащим к - ми l - м CC; таким образом, могут быть установлены плотности барьеров, образующихся в ходе реакций и являющихся компонентами матрицы Rkl , позволяющей учитывать взаимодействие дислокаций обоих знаков. При формулировке закона упрочнения принимается гипотеза о возможности аддитивного разделения критических напряжений СС на вклады от сопротивления решётки (величина, зависящая только от температуры), от полей напряжений дислокаций и от образованных на расщеплённых дислокациях барьеров [62]. Для определения составляющей, описывающей влияние накопленных дефектов, оценивалось взаимодействие полей напряжений дислокаций различных СС друг с другом. Для этого использовалось известное из [35] решение для поля напряжений одиночной дислокации и его действие на другую дислокацию в изотропной упругой среде. На его основе строилась матрица Mki , позволяющая оценить напряжения взаимодействия дислокаций k -й и i -й СС, которые заносятся на пересечении k -й строки и i -го столбца матрицы Mki . Введение барьера, образуемого расщеплёнными дислокациями, как комплекса, состоящего из двух частичных и одной сидячей дислокации, позволило оценить его влияние на упрочнение на k -й СС за счёт барьера на i -й СС; для описания этого влияния строится матрица Вki , подобная матрице Mki. Компоненты матриц нормируются на начальные критические напряжения соответствующих СС (на напряжения Пайерлса) т(k) = т(k\at и становятся безразмерными величинами. С использованием принятых матриц эволюционные соотношения для изменения критического напряжения сдвига и его составляющих можно записать в следующем виде [63]: Bki n t!“......= в ь .0^ где а, в — безразмерные параметры материала. Вышеизложенный материал позволяет дать следующее краткое описание общей структуры модели, уровней и связей между ними. Итак, элемент макроуровня (представительный макрообъём) включает конечное множество (несколько сотен) элементов мезоуровня-1 (кристаллитов), имеющих различные ориентации решётки по отношению к характерным осям нагружения (и к осям лабораторной системы координат); каждый элемент мезоуровня-1 по масштабу совпадает с элементом мезоуровня-2. С макроуровня на мезоуровень-1 передаются воздействия (градиент скорости перемещений, температура). На мезоуровне-1 процессы деформирования представляются в терминах механических переменных (в напряжениях, деформациях, их скоростях). С мезоуровня-1 на мезоуровень-2 в качестве воздействия передаются касательные напряжения по СС и температура; описание на мезуровне-2 осуществляется в терминах плотностей и скоростей движения дислокаций. По величинам последних из уравнения Орована отыскиваются скорости сдвигов по СС и неупругая составляющая меры скорости деформации, которые транслируются на мезоуровень-1. На мезоуровне-1 по полному градиенту скорости перемещений и его неупругой составляющей устанавливается спин жёсткой подвижной системы координат и скорости изменения напряжений (с использованием упругого закона в скоростной релаксационной форме). Осреднением по элементам мезоуровня-1 получаются скорости изменения напряжений на макроуровне. 3. Алгоритм реализации модели При реализации модели, в силу нелинейности задачи исследования пластического деформирования, применяется пошаговая процедура. Полное время процесса t е [0, tk ] разбивается на ряд шагов, решение представляется в виде последовательности искомых в моменты времени 0 (при начальных данных), At, 2At, ..., MAt = tk решений. Величина шага At устанавливается из численных экспериментов с постепенным его уменьшением до достижения в момент t фробениусовой нормой разности тензоров макронапряжений соответствующих двум последовательным временным шагам t значения, не превышающего на 1% наибольшую (из двух сравниваемых) интенсивностей напряжений. Перед началом расчётов задаются необходимые начальные условия и материальные параметры для переменных всех уровней. Следует особо выделить первый шаг нагружения. На нём, в силу предположения о естественном (ненапряженном и недеформированном) состоянии материала, в отсчётной конфигурации отклик кристаллитов описывается упругими соотношениями, следовательно, в этом случае достаточно ограничиться вычислениями только с использованием подмодели мезоуровня-1. Как отмечено в конце предыдущего раздела, отклик материала на уровне представительного макрообъёма определяется осреднением по объёму соответствующих параметров мезоуровня-1, напряжения и повороты рассчитываются на основе подмоделей мезо-1 и мезо-2. Необходимо напомнить, что вычисления тензорных величин осуществляются в терминах компонент в базисе жёсткой подвижной системы координат (ПСК), связанной со структурной решёткой материала, что позволяет применять обычные операции дифференцирования и интегрирования вместо коротационных. В случае завершения вычислений на предыдущем шаге (t—At ) к моменту начала шага при времени t известны все переменные (компоненты тензоров напряжений (в базисе ПСК), плотности дислокаций и барьеров, критические напряжения на СС). Схема алгоритма реализации модели на шаге t представлена на рисунке 2. Как видно, решение реализуется в три этапа: а) осуществляется решение в скоростях; б) интегрируются скоростные Интегрирование всех внутренних переменных (этап б), переопределение ориентации ПСК, тензорзначных ВП, определение компонент тензоров в базисе лабораторной системы координат (этап в), переход на шаг t + At Шаг 1 О Zt (t) i элемент мезо -1, i=1, N (этап z,(t ) = Z (t ) (k) i+1, t-At а)т(+>t-At = b(k)n(k): G t-At 4. Некоторые результаты применения модели Рис. 2. Схема к алгоритму реализации модели на произвольном шаге по времени характеристики и определяются параметры на конец шага; в) находятся ориентации ПСК и компоненты тензоров преобразуются в базисе ПСК. На этапе а) по напряжениям, температуре, плотностям дислокаций и барьеров, критическим напряжениям сдвига, установленным к началу текущего шага по времени, с использованием соотношений подмодели мезоуровня-2 вычисляются скорости движения дислокаций по СС, равно как скорости изменения всех внутренних переменных (плотностей дислокаций и барьеров и других). С помощью уравнения Орована определяются неупругие составляющие меры скорости деформации в кристаллитах, после чего с учётом гипотезы Фойгта находятся упругие составляющие последней. Далее в рамках подмодели мезоуровня-1 рассчитываются скорости изменения компонент тензора напряжений (в базисе ПСК) и спины ПСК всех кристаллитов. На этапе б) на основе скоростных характеристик, установленных на этапе а), с помощью любой из известных схем (в настоящей работе — это явная схема Эйлера) осуществляется интегрирование всех параметров подмоделей мезо-1 и мезо-2 (в том числе тензоров ориентаций ПСК кристаллитов), находятся их значения на конец текущего шага (компоненты тензоров — в базисе ПСК). Наконец, на этапе в) с использованием ориентационных тензоров ПСК определяются тензорные переменные уровней мезо-1 и мезо-2, причем их компоненты — в базисе единой для всех кристаллитов лабораторной системе координат, и вычисляются осреднённые по представительному макрообъёму параметры. После этого происходит переход к следующему (t+At) временному шагу. Разработанная модель использована для описания отклика поликристаллических макрообразцов с ГЦК–решёткой, подвергаемых простому и сложному циклическим нагружениям. Представительный объём макроуровня (макрообразец) состоял из 343 кристаллитов с распределением их в отсчётной конфигурации по равномерному закону. Численные эксперименты проводились на модельных макрообразцах из нержавеющей стали SAE 310S с энергией ДУ 20 мДж/м2. Начальные плотности дислокаций полагались одинаковыми и равными 109 м–2, начальные плотности барьеров равнялись нулю. Нагружения в численных опытах рассматривались циклические (простое и сложное) и осуществлялись кинематически, деформации при этом ограничивались их максимальными амплитудными значениями по интенсивности. Основная цель исследования заключаласяь в анализе отклика материала в опытах на нагружения с различными по сложности траекториями деформаций в пространстве деформаций А.А. Ильюшина. При расчётах программа воздействия включала пропорциональное и непропорциональные нагружения; для сравнения теоретических результатов с результатами натурных экспериментов использовалась данные испытаний трубчатых образцов из стали AISI 304 (ГОСТ 08Х18Н10), приведённые в [42]. Идентификация параметров закона упрочнения выполнялась на основе данных программ пропорционального и непропорционального (по эллиптической траектории деформации) нагружений и сводилась к задаче нелинейного программирования, для решения которой применялся метод Нелдера–Мида; в качестве целевой функцией выступал модуль разности вышедших на стационарные значения амплитуд интенсивностей напряжений, установленных экспериментально и с помощью предлагаемой модели. В ходе идентификации параметров по экспериментам на простое циклическое деформирование (пропорциональное растяжение–сжатие и сдвиг) найдено значение параметра а = 3,4 (см. (10)3), так как при простых нагружениях упрочнение происходит в основном за счёт взаимодействия дислокаций. Параметры у и в, входящие, соответственно, в соотношения (9)1 и (10)4, определялись с помощью численных экспериментов на сложное нагружение (по эллиптическим траекториям), для которых присущи взаимодействия дислокаций пересекающихся СС с образованием барьеров Ломера-Коттрелла и Хирта; получены следующие значения: в = 137,8 и у = 8,9 -10 —5 . Верификация модели выполнена с использованием экспериментальных данных по программам деформирования с траекториями в форме квадрата со стороной, равной деформации 0,5%; амплитудные значения интенсивности напряжений при выходе на стационарный режим в натурном эксперименте равнялись 432 МПа. Результаты моделирования дали значение 424,7 МПа, что позволяет считать модель применимой для исследования процессов сложного нагружения. Следует отметить, что в силу малой величины энергии ДУ для исследуемой стали характерно образование барьеров на расщеплённых дислокациях, что отражается в увеличении уровня упрочнения материалов с низкой энергией ДУ (по сравнению с материалами с высокой энергией ДУ). Средние плотности барьеров достигли порядка 105 м–2 для деформирования по траектории в форме квадрата, что превышает соответствующее значение на 38% при простом циклическом нагружении и на 33% при нагружении по эллиптической траектории; увеличение плотности барьеров наиболее активно происходит в диапазоне от 50 до 100% в абсолютных накопленных деформациях. При сравнении результатов работы модели с учётом и без учёта влияния образованных барьеров показано, что при «выключении» вклада барьеров (без члена т(k\аг в (10)4) уровень критических — напряжений и интенсивностей напряжений понижается в зависимости от типа нагружения на 20–30%. На иллюстрациях (Рис. 3–5) изображены зависимости первой и второй компонент вектора деформаций в пространстве деформаций А.А. Ильюшина ( E , E ) и зависимость интенсивности напряжений S от интенсивности накопленной деформаций E . На фрагментах (б) показаны интенсивности напряжений как функции интенсивности накопленных деформаций (области синего цвета, для наглядности на них наложены увеличенные части графиков, во вставках с «растянутой» по интенсивности деформаций шкалой). Компоненты E и E определяются путём интегрирования меры скорости деформации z и перехода к векторным независимым переменным — компонентам в пятимерном пространстве Ex — Е5 [5, 11]. Наибольший интерес представляет оценка величины дополнительного упрочнения при разном типе нагружения (при фиксированных одинаковых амплитудах интенсивности деформации) для материалов с различной энергией ДУ. Следует отметить, что для готовых изделий, как правило, допустимой областью эксплуатации является такое множество параметров их напряжённо-деформированного состояния, которые не выходят за пределы упругости. Область упругих деформаций обычно определяется условием Мизеса, формулируемым в терминах интенсивности напряжений и напряжения течения. Если на заключительных стадиях изготовления изделий применяется циклическое нагружение, то с повышением предела текучести материала увеличивается диапазон допустимых воздействий (напряжений и деформаций) при их последующей эксплуатации. В ходе численных экспериментов с использованием заданных кинематических воздействий находились максимальные интенсивности напряжений (после выхода на стационарные значения кривой «амплитудные напряжения–накопленные деформации»). Численные эксперименты показали, что циклическое деформирование по сложным траекториям приводит к существенному дополнительному (по сравнению с простым циклическим нагружением при тех же Рис. 3. Траектория деформации при пропорциональном нагружении (растяжение–сжатие) (а) в двумерном подпространстве пятимерного пространства деформаций А.А. Ильюшина и зависимость интенсивности напряжений (б) от интенсивности накопленных деформаций при данном нагружении; прямая чёрная линия – уровень интенсивности напряжений при установившемся режиме, определённый экспериментально в [42] Рис. 4. Траектория деформации при непропорциональном растяжении–сжатии (а) в двумерном подпространстве пятимерного пространства деформаций А.А. Ильюшина и зависимость интенсивности напряжений (б) при нагружении представительного макрообъёма стали от интенсивности накопленных деформаций при соответствующем нагружении; прямая чёрная линия – уровень интенсивности напряжений при установившемся режиме, определённый экспериментально [42] % 0,2 0,1 -0,1 -0,2 Рис. 5. Траектория деформации (растяжение–сжатие) в форме квадрата (а) в двумерном подпространстве пятимерного пространства деформаций А.А. Ильюшина и зависимость интенсивности напряжений (б) в представительном макрообъёме стали от интенсивности накопленных деформаций при указанном нагружении; прямая чёрная линия – уровень интенсивности напряжений при установившемся режиме, определённый экспериментально [42] а б значениях амплитуды деформаций) упрочнению (см. Рис. 3–5, фрагменты (б)). Это характерно для материалов с низкой энергией ДУ. Кривая «амплитуда интенсивности напряжения–интенсивность накопленных деформаций» (огибающая максимумы на диаграмме циклического нагружения) выходит на стационарные значения при достижении интенсивностью накопленных деформаций уровня от 90 до 140%. Существенный вклад в повышение напряжения течения (в упрочнение) вносит образование барьеров на расщеплённых дислокациях. Соответствие результатов расчёта экспериментальным данным из работ [27, 29, 42] (прямая чёрная линия, см. Рис. 3–5, фрагменты (б)), позволяет констатировать принципиальную применимость разработанной модели для описания процессов циклического, в том числе сложного, нагружения материалов с различной величиной энергии ДУ. Найденные в процессе идентификации (с использованием данных по пропорциональному и непропорциональному нагружению по эллиптической траектории) параметры модели позволили получить количественно согласующиеся результаты: для деформирования по замкнутому контуру в форме квадрата (в двумерном подпространстве пятимерного пространства деформаций А.А. Ильюшина): по амплитуде интенсивности напряжений в установившемся режиме различие теоретических и экспериментальных данных составляет около 2% (7,3 МПа). 5. Заключение Рассмотрена структура и математическая формулировка трёхуровневой конститутивной модели, основанной на введении внутренних переменных и физической дислокационно-ориентированной теории упруговязкопластичности. Особое внимание уделено описанию взаимодействия дислокаций и образованию барьеров дислокационной природы (Ломера–Коттрелла, Хирта). С формированием последних связывается экспериментально установленный и подтверждённый расчётами эффект дополнительного циклического упрочнения при деформировании по сложным замкнутым траекториям деформации, характерный для сплавов с низкой энергией дефекта упаковки. Приведено краткое описание алгоритма реализации модели. В рамках подготовки материала к опубликованию осуществлены численные эксперименты по циклическому нагружению образцов при простых и сложных траекториях деформации. Результаты расчётов обнаруживают удовлетворительное качественное и количественное соответствие экспериментальным данным, что подтверждает применимость разработанной модели для анализа процессов сложного (на макроуровне) нагружения. Работа выполнена при финансовой поддержке Министерства науки и высшего образования РФ (базовая часть государственного задания ПНИПУ, проект № FSNM-2020-0027).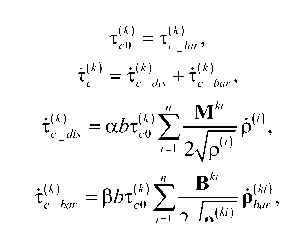
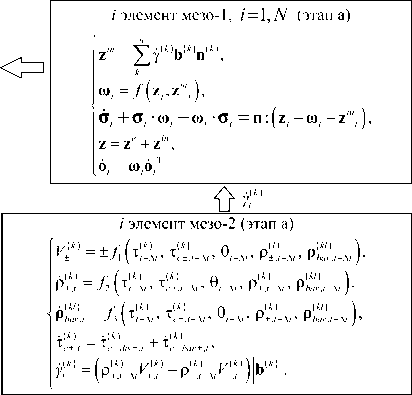
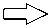
Список литературы Трёхуровневая модель, основанная на физических теориях пластичности: формулировка, алгоритмы реализации, результаты применения для исследования циклического нагружения
- Лихачев В.А., Малинин В.Г. Структурно-аналитическая теория прочности. СПб.: Наука, 1993. 471 с.
- Физическая мезомеханика и компьютерное конструирование материалов / Отв. ред. В.Е. Панин. Новосибирск: Наука, 1995. Т. 1. 298 с.
- Физическая мезомеханика и компьютерное конструирование материалов / Отв. ред. В.Е. Панин. Новосибирск: Наука, 1995. Т. 2. 320 с.
- Трусов П.В., Швейкин А.И. Теория пластичности. Пермь: Изд-во ПНИПУ, 2011. 419 с.
- Ильюшин А.А. Пластичность. Основы общей математической теории. М.: АН СССР, 1963. 272 с.
- Качанов Л.М. Основы теории пластичности. М.: Наука, 1969. 420 с.
- Соколовский В.В. Теория пластичности. М.: Высшая школа, 1969. 608 с.
- Васин Р.А. Определяющие соотношения теории пластичности // Итоги науки и техники. Сер. Механика деформируемого твердого тела. 1990. Т. 21. С. 3-75.
- Бондарь В.С. Неупругость. Варианты теории. М.: Физматлит, 2004. 144 с.
- Васин Р.А. Свойства функционалов пластичности у металлов, определяемые в экспериментах на двузвенных траекториях деформации // Упругость и неупругость. М.: МГУ, 1987. С. 115-127.
- Зубчанинов В.Г. Основы теории упругости и пластичности. М.: Высшая школа, 1990. 368 с.
- Аннин Б.Д., Жигалкин В.М. Поведение материалов в условиях сложного нагружения. Новосибирск: Изд-во СО РАН, 1999. 342 с.
- Rice J.R. Inelastic constitutive relations for solids: An internal-variable theory and its application to metal plasticity // J. Mech. Phys. Solids. 1971. Vol. 19. P. 433-455. https://doi.org/10.1016/0022-5096(71)90010-X
- Можен Ж. Механика электромагнитных сплошных сред. М.: Мир, 1991. 560 с.
- McDowell D.L. Internal state variable theory // Handbook of materials modeling / Ed. S. Yip. Springer, 2005. P. 1151-1169. https://doi.org/10.1007/978-1-4020-3286-8_58
- Ашихмин В.Н., Волегов П.С., Трусов П.В. Конститутивные соотношения с внутренними переменными: общая структура и приложение к текстурообразованию в поликристаллах // Вестник ПГТУ. Математическое моделирование систем и процессов. 2006. № 14. С. 11-26.
- Horstemeyer M.F., Bammann D.J. Historical review of internal state variable theory for inelasticity // Int. J. Plast. 2010. Vol. 26. Р. 1310-1334. https://doi.org/10.1016/j.ijplas.2010.06.005
- Maugin G.A. The saga of internal variables of state in continuum thermo-mechanics (1893-2013) // Mech. Res. Comm. 2015. Vol. 69. P. 79-86. https://doi.org/10.1016/j.mechrescom.2015.06.009
- Taylor G.I. Plastic strain in metals // J. Inst. Metals. 1938. Vol. 62. P. 307-324.
- Lin P., El-Azab A. Implementation of annihilation and junction reactions in vector density-based continuum dislocation dynamics // Modelling Simul. Mater. Sci. Eng. 2020. Vol. 28. 045003. https://doi.org/10.1088/1361-651X/ab7d90
- Asaro R.J., Needleman A. Texture development and strain hardening in rate dependent polycrystals // Acta Metall. 1985. Vol. 33. P. 923-953. https://doi.org/10.1016/0001-6160(85)90188-9
- Horstemeyer M.F. Multiscale modeling: A review // Practical aspects of computational chemistry / Ed. J. Leszczynski, M.K. Shukla. Springer, 2009. Р. 87-135. https://doi.org/10.1007/978-90-481-2687-3_4
- McDowell D.L. A perspective on trends in multiscale plasticity // Int. J. Plast. 2010. Vol. 26. Р. 1280-1309. https://doi.org/10.1016/j.ijplas.2010.02.008
- Roters F. Advanced material models for the crystal plasticity finite element method: Development of a general CPFEM framework. Aachen: RWTH Aachen, 2011. 226 р.
- Трусов П.В., Швейкин А.И. Многоуровневые модели моно- и поликристаллических материалов: теория, алгоритмы, примеры применения. Новосибирск: Изд-во СО РАН, 2019. 605 с.
- Dupuy L., Fivel M.C. A study of dislocation junctions in FCC metals by an orientation dependent line tension model // Acta Mater. 2002. Vol. 50. P. 4873-4885. https://doi.org/10.1016/s1359-6454(02)00356-7
- Krempl E., Lu H. Comparison of the stress responses of an aluminum alloy tube to proportional and alternate axial and shear strain paths at room temperature // Mech. Mater. 1983. Vol. 2. P. 183-192. https://doi.org/10.1016/0167-6636(83)90013-3
- Tanaka E., Murakami S., Ooka M. Effects of plastic strain amplitudes on non-proportional cyclic plasticity // Acta Mech. 1985. Vol. 57. P. 167-182. https://doi.org/10.1007/BF01176916
- Doquet V. Twinning and multiaxial cyclic plasticity of a low stacking-fault-energy f.c.c. alloy // Acta Metall. Mater. 1993. Vol. 41. P. 2451-2459. https://doi.org/10.1016/0956-7151(93)90325-M
- Zubchaninov V.G., Okhlopkov N.L. Hardening of structural materials in the process of complex deformation along closed plane trajectories // Strength of Mater. 1997. Vol. 29. P. 220-228. https://doi.org/10.1007/BF02767438
- Itoh T., Nakata T., Sakane M., Ohnami M. Nonproportional low cycle fatigue of 6061 aluminum alloy under 14 strain paths // European Structural Integrity Society. 1999. Vol. 25. P. 41-54. https://doi.org/10.1016/S1566-1369(99)80006-5
- Anes V., Reis L., Li B., de Freitas M. New approach to evaluate non-proportionality in multiaxial loading conditions // Fatig. Fract. Eng. Mater. Struct. 2014. Vol. 37. P. 1338-1354. https://doi.org/10.1111/ffe.12192
- Anes V., Reis L., Li B., Fonte M., de Freitas M. New approach for analysis of complex multiaxial loading paths // Int. J. Fatig. 2014. Vol. 62. P. 21-33. https://doi.org/10.1016/j.ijfatigue.2013.05.004
- Rohatgi A., Vecchio K.S., Gray G.T. III The influence of stacking fault energy on the mechanical behavior of Cu and Cu-Al alloys: Deformation twinning, work hardening, and dynamic recovery // Metall. Mater. Trans. A. 2001. Vol. 32. P. 135-145. https://doi.org/10.1007/s11661-001-0109-7
- Фридель Ж. Дислокации. М.: Мир, 1967. 644 с.
- Хоникомб Р. Пластическая деформация металлов. М.: Мир, 1972. 408 с.
- Новиков И.И. Дефекты кристаллического строения металлов. М.: Металлургия, 1975. 208 с.
- Kanazawa K., Miller K.J., Brown M.W. Cyclic deformation of 1% Cr-Mo-V steel under out-of-phase loads // Fatig. Fract. Eng. Mater. Struct. 1979. Vol. 2. P. 217-228. https://doi.org/10.1111/j.1460-2695.1979.tb01357.x
- Ohashi Y., Tanaka E., Ooka M. Plastic deformation behavior of type 316 stainless steel subject to out-of-phase strain cycles // J. Eng. Mater. Technol. 1985. Vol. 107. P. 286-292. https://doi.org/10.1115/1.3225821
- Krempl E., Lu H. The hardening and rate-dependent behavior of fully annealed AISI type 304 stainless steel under biaxial in-phase and out-of-phase strain cycling at room temperature // J. Eng. Mater. Technol. 1984. Vol. 106. P. 376-382. https://doi.org/10.1115/1.3225733
- Doong S.-H., Socie D.F., Robertson I.M. Dislocation substructures and nonproportional hardening // J. Eng. Mater. Technol. 1990. Vol. 112. P. 456-464. https://doi.org/10.1115/1.2903357
- Doong S.-H., Socie D.F. Constitutive modeling of metals under nonproportional cyclic loading // J. Eng. Mater. Technol. 1991. Vol. 113. P. 23-30. https://doi.org/10.1115/1.2903379
- Borodii M.V., Shukaev S.M. Additional cyclic strain hardening and its relation to material structure, mechanical characteristics, and lifetime // Int. J. Fatig. 2007. Vol. 29. P. 1184-1191. https://doi.org/10.1016/j.ijfatigue.2006.06.014
- Bees M.R., Pattison S.J., Fox N., Whittaker M.T. The non-proportional behaviour of a nickel-based superalloy at room temperature, and characterisation of the additional hardening response by a modified cyclic hardening curve // Int. J. Fatig. 2014. Vol. 67. P. 134-141. https://doi.org/10.1016/j.ijfatigue.2014.02.023
- Shang D.-G., Wang D.-J., Yao W.-X. A simple approach to the description of multiaxial cyclic stress-strain relationship // Int. J. Fatig. 2000. Vol. 22. P. 251-256. https://doi.org/10.1016/S0142-1123(99)00117-6
- Gates N.R., Fatemi A. A simplified cyclic plasticity model for calculating stress-strain response under multiaxial non-proportional loadings // Eur. J. Mech. Solids. 2016. Vol. 59. P. 344-355. http://dx.doi.org/10.1016/j.euromechsol.2016.05.001
- Yuan F., Chen P., Feng Y., Jiang P., Wu X. Strain hardening behaviors and strain rate sensitivity of gradient-grained Fe under compression over a wide range of strain rates // Mech. Mater. 2016. Vol. 95. P. 71-82. https://doi.org/10.1016/j.mechmat.2016.01.002
- Lei C., Deng X., Li X., Wang Z., Wang G., Misra R.D.K. Mechanical properties and strain hardening behavior of phase reversion-induced nano/ultrafine Fe-17Cr-6Ni austenitic structure steel // J. Alloy. Comp. 2016. Vol. 689. P. 718-725. http://dx.doi.org/10.1016/j.jallcom.2016.08.020
- Shao C.W., Zhang P., Zhu Y.K., Zhang Z.J., Tian Y.Z., Zhang Z.F. Simultaneous improvement of strength and plasticity: Additional work-hardening from gradient microstructure // Acta Mater. 2018. Vol. 145. P. 413-428. https://doi.org/10.1016/j.actamat.2017.12.028
- Xia S., El-Azab A. Computational modelling of mesoscale dislocation patterning and plastic deformation of single crystals // Modelling Simul. Mater. Sci. Eng. 2015. Vol. 23. 055009. https://doi.org/10.1088/0965-0393/23/5/055009
- Knezevic M., Beyerlein I. Multiscale modeling of microstructure-property relationships of polycrystalline metals during thermo-mechanical deformation // Adv. Eng. Mater. 2018. Vol. 20. 1700956. https://doi.org/10.1002/adem.201700956
- Bergström Y. A dislocation model for the stress-strain behaviour of polycrystalline α-Fe with special emphasis on the variation of the densities of mobile and immobile dislocations // Materials Science and Engineering. 1970. Vol. 5. P. 193-200. https://doi.org/10.1016/0025-5416(70)90081-9
- Sudmanns M., Bach J., Weygand D., Schulz K. Data-driven exploration and continuum modeling of dislocation networks // Modelling Simul. Mater. Sci. Eng. 2020. Vol. 28. 065001. https://doi.org/10.1088/1361-651X/ab97ef
- Трусов П.В., Швейкин А.И. О разложении движения и определяющих соотношениях в геометрически нелинейной упруговязкопластичности кристаллитов // Физ. мезомех. 2016. Т. 19, № 3. С. 25-38. (English version https://doi.org/10.1134/S1029959917040026)
- Khan A.S., Liu J. A deformation mechanism based crystal plasticity model of ultrafine grained/nanocrystalline FCC polycrystals // Int. J. Plast. 2016. Vol. 86. P. 56-69. https://doi.org/10.1016/j.ijplas.2016.08.001
- Orowan E. Problems of plastic gliding // Proc. Phys. Soc. 1940. Vol. 52. P. 8-22. https://doi.org/10.1088/0959-5309/52/1/303
- Kocks U.F. Constitutive behavior based on crystal plasticity // Unified constitutive equations for creep and plasticity / Ed. A.K. Miller. Springer, 1987. P. 1-88. https://doi.org/10.1007/978-94-009-3439-9_1
- Trusov P.V., Gribov D.S. The three-level elastoviscoplastic model and its application to describing complex cyclic loading of materials with different stacking fault energies // Materials. 2022. Vol. 15. 760. https://doi.org/10.3390/ma15030760
- Орлов А.Н. Введение в теорию дефектов в кристаллах. М.: Высшая школа, 1983. 144 с.
- Cho J., Molinari J.-F., Anciaux G. Mobility law of dislocations with several character angles and temperatures in FCC aluminum // Int. J. Plast. 2017. Vol. 90. P. 66-75. https://doi.org/10.1016/j.ijplas.2016.12.004
- Штремель М.А. Прочность сплавов. Ч. I. Дефекты решетки. М.: МИСИС, 1999. 384 с.
- Yi H.Y., Yan F.K., Tao N.R., Lu K. Work hardening behavior of nanotwinned austenitic grains in a metastable austenitic stainless steel // Scripta Mater. 2016. Vol. 114. P.133-136. https://doi.org/10.1016/j.scriptamat.2015.12.021
- Madec R., Devincre B., Kubin L.P. Simulation of dislocation patterns in multislip // Scripta Mater. 2002. Vol. 47. P. 689-695. https://doi.org/10.1016/S1359-6462(02)00185-9


