Two-Level Alloyed Branch Predictor based on Genetic Algorithm for Deep Pipelining Processors

Published Online May 2017 in MECS

High-performance computers are embedded with the processors with deeper pipelining and also with higher parallelism in instruction fetch, and are called superscalar processors. The Increment in instruction fetch parallelism causes control and data hazards. Data forwarding units can be implemented to remove data hazards whereas branch predictors deal with control hazards. A lot of cycles get wasted in a single miss-prediction, that’s why we need branch predictors having very high level of accuracy. One way of deploying this is to make adaptive branch predictor [11]. Such predictor uses the information about the behavior of a branch for fixed number of iterations (local history) or/and behavior of fixed number of past branches (global history) stored in it at the time of execution [3]. The new way of dealing with this problem is to use multiple advanced dynamic branch predictors in the same structure to maintain the accuracy of prediction throughout. This idea came into existence because every branch predictor has its characteristics and behaves differently with the change in frequency of branch directions. Branch prediction is an on-going subject.

Branch prediction is also a point of interest for many researchers. There are several ways of deploying the branch predictors, but two-level alloyed predictor is considered to be most accurate [7]. The technique that a highly accurate predictor uses is recording the branch history and observing each branch scenario which predictor came across. Predictor learns from these scenarios and starts predicting better. Static selection is undesirable as the direction of individual branches varies dynamically, and there could be a need for both global and local history [1].

The need for global and local history made alloyed branch prediction technique came into existence. Alloying gives higher prediction accuracy over conventional branch predictors with the addition of nominal hardware to store branch/branches history. No advancement in prediction mechanism limits alloying technique to get efficiencies ranging in 70%-95% and in some situations the miss-prediction rate can be as high as 35%. A new source of miss-prediction comes into account if we deploy components for both local and global history [9]. This miss-prediction happens when branch needs local history and predictors track the global one or vice-versa and hence poor behavior. This kind of prediction is called wrong-history miss-prediction. The Wrong history here doesn’t mean that history bits are wrong, but the track is inappropriate for a particular branch [3]. Separate structures for global and local history can solve this problem but still alloyed branch predictor lacks in good prediction mechanism. This lacking in accuracy is the reason why alloyed predictors use other schemes such as Tournament predictors or Genetic Programming to increase performance. An energy efficient branch predictor with less history size and self-learning capacity is our goal so that the predictions will become more robust and dynamic according to change in frequency of branch direction in instruction fetch.

This paper explains why and when our predictor performs well. The Genetic algorithm with a particular fitness function we have chosen works well for the class of continuously flipping branches (if-else branches) along with those branches whose flipping tendency is very less (loop branches). We know that programs tend to have branches, of which, these two kinds frequently occur but when they do not, our predictor may not perform as well as other techniques. Thus, our predictor works best in the conditions where branch transition probabilities are either too high or too less.

Our predictor gives a hike in performance and reaches the accuracies as high as 98% with the128K budget in the two extreme cases mentioned above. On the other hand for other cases, the performance is not remarkable, and mispredictions rate reaches to 20-25%.

This paper makes the following contributions. In section-I, we introduce the basic branch problem and validation of scheme proposed in this paper. In section-II, we provide a deep literature survey, which explains a wide variety of branch resolving techniques and covers major related work. Furthermore, in section-III, we proceed in our paper by giving a thorough explanation of how to integrate genetic algorithm in branch prediction. This section also explains genetic operations involved in GA. In section IV we explained the whole methodology, which we have used while integrating genetic algorithm with alloyed branch predictor. This section focuses on modeling GA and explains how genetic operations work to select the best predictor in present situation. Section V includes results of our simulations and performance comparison of conventional branch predictors with proposed predictor has been done. Lastly, in section VI we concluded the performance analysis done in the previous section. This section also gives the validation of proposed work. Tabulated results are attached at the end of the paper.

• II.    Related Works

The literature on branch prediction schemes is huge [13][2][11][14][4][6]. Few of them from deep past were based on static predictions while others were dynamic in nature i.e. predictors which change its behavior in runtime. Researchers have done Substantial research to decrease aliasing problem, power consumption problem, delay and hardware in branch predictors [15][1][3]. Bi-Modal branch predictor [13] is the simplest dynamic branch predictor. It is more accurate than one-bit branch predictor and one of the most widely used predictors. The accuracy of this predictor depends on the dynamic behavior of the branch, which limits the accuracy to 50% [2]. It also has a high level of aliasing in PHT (Pattern history table) that affects the accuracy. Two-level Adaptive Branch predictors and hybrid predictors such as YAGS (Yet Another Global Scheme) branch predictors can improve efficiency. These predictors consume less power and have improved accuracy with little aliasing

[11][15][16]. The main advantage we get from the adaptive or dynamic branch predictor is they learn the repetitive pattern of change in branch direction if any, studies the branch behavior and acts accordingly. It does not alter its prediction very quickly but changes with changing scenario [11].

A more accurate 2 level branch predictor, which takes the recent behavior of other branches into consideration, is called Correlating branch predictor [2][14]. A previously executed branch can affect the direction and outcome of the future branch if a previous branch runs source operands of the next branch. Correlated branch predictor handles these correlations between the branches and improves prediction mechanism by identifying the correlated branches from large history table. G-share branch predictor eradicates the problem of aliasing [12] in earlier branch predictors. When multiple branches mapped onto the same location in branch history table, it is called aliasing. Therefore, many positions of branch history table remain unmapped. G-share branch predictor [2] uses the XOR function to produce new bits, which will further point to the different locations in the history table. In G-share prediction mechanism XORing of ‘k’ least significant bits of current PC address is being done with address bits of global history table [9]. This XORing gives a new address, which will point to a unique location of branch history table and we take prediction bit of that address to predict the current branch. Generation of unique address every time in G-share predictors prevents aliasing. Removal of aliasing helps in increasing the prediction accuracy but with a margin of 2-5%, and there is still a scope to recuperate the branch prediction techniques and algorithms [4]. The right amount of research on resolving multiple branches in a single cycle has also been done in recent past [17].

Alloyed branch prediction has its importance in its robustness in using the local and global history in the same structure. Alloyed or hybrid predictors are designed to fulfill the requiring need of improvement in the accuracy of predictors and also its an effort to develop a structure to predict branches (T/NT) more dynamically. Alloyed predictors changed the prediction mechanism slightly which was earlier unaltered in conventional branch predictors [6]. Hybrid predictors with different PHT for taken and not taken branches are efficient enough to improve prediction accuracy but with a large hardware budget.

Branch prediction structures that use more than two single scheme predictors were introduced in the past. These predictors use two kinds of predictors: one with less warm-up time along with those who have highest prediction efficiency but have great warm-up time. These predictors are made keeping the fact in mind that most efficient predictors have large history tables and they need training time to get higher accuracies i.e. warm-up time of these predictors are large. Hybrid predictors [18] Initially use small single scheme predictor with less warm-up time. In the meantime, the history table gets filled with enough prediction bits to train the other predictor embedded in the structure. This predictor then uses this history to predict with better accuracy and maintain it. Predictor that uses neural networks (perceptrons) has also been proposed [5]. These predictors with machine learning techniques are more sophisticated than conventional predictors. They claim to give higher accuracies of prediction in nominal hardware budget (4K byte).

• III.    Branch Prediction With Genetic Algorithm (GA)

Branch prediction with GA is a new way to predict the branch direction (T/NT). GA has a knack to generate potential solutions and to improve them, as it evolves. GA is all about moving to the fittest solutions and maintaining the selection of the same. This property of GA motivates us to design an environment, where GA selects the most suitable predictor to be used and also picks up the prediction bit of the same predictor [5].

• A.    Why GA

The motivation of integrating our primary alloyed branch prediction mechanism with the GA is to improve the conventional prediction scheme and to have a substantial growth in prediction accuracy. GA is efficient in elucidating two of the biggest problems, which we come across while predicting through conventional Hybrid predictors: One is how to know which predictor is making the correct predictions and the second is how to ensure that the prediction bit generated by our conventional predictors is right in the present scenario. GA does this job efficiently as we can encode the type of predictor with its characteristics in the binary string that are called chromosomes. The genetic operations help us in selecting the winner chromosome. The prediction of the predictor encoded in the winner chromosome can then be made.

• B.    How GA Works

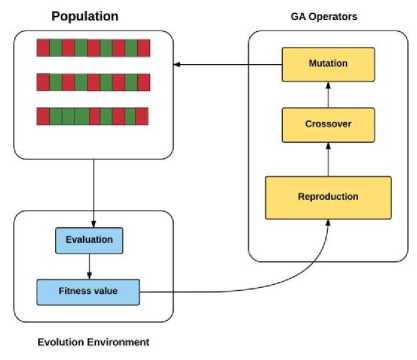
Fig.1. GA mechanism

Generating Initial Population- The very first step in GA is to create an initial population of solutions, which we call chromosomes. These chromosomes are the binary strings as shown in Figure 4 whose bits are the properties of the different predictors such as the warm-up time, more accurate predictor, and probability difference between the last few taken/not-taken branches.

Applying Fitness Function- The next step is to find the winner chromosome among all the chromosomes selected and for this, we use fitness function over our chromosomal strings as shown in the second phase of Figure 4. The fittest chromosome is selected and the prediction bit of the predictor encoded in the winner chromosome is taken into account [8].

Mutation -Mutation is done on a single bit or multiple points of current generation. It is a step to prevent convergence in multiple offspring. Mutation is done in the binary chromosomal string to flip few of the bits, which will try to make every new generation unique [8].

Crossover - Crossover is done to copy useful bits from winner chromosome to other offspring. It is done to generate healthier future generation from the recipient chromosome. In this way, the new generation produced will be healthier than the old generation of solutions [8].

• IV.    Proposed Methodology

The use of 2-bit counter in traditional predictors such as correlated and G-share gives miss-prediction whenever counter is at corrupt state. This type of miss-prediction reduces the accuracy. Which led us to create a mechanism, which can work accurately even when the counter goes wrong. Integrating GA with alloyed predictor does the same. GA not only selects the prediction bit of best predictor but also tries to predict branch correctly when selected predictor fails. So in this way scope of wrong predictions decreases. The criterion of prediction used by GA in the cases when the counter goes wrong is to calculate probability difference of last 8 T/NT branches. GA gives its forecast as taken if the probability of the number of taken branches is more or vice-versa.

• A. GA Implementation

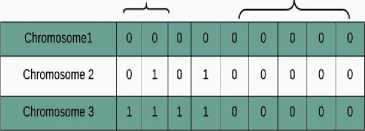
GA starts with encoding binary strings called chromosomes, and each chromosomal string contains 9 bits, and each bit has its significant meaning regarding the features of predictor: Starting two bits signifies the type of predictor: (00) for bi-modal, (01) for G-share, (11) for correlated predictor. Next, two bits mean the wake-up time of the particular predictor. The wake-up time is highest for bi-modal and lowest for the correlated predictor, therefore initially (00) is used for highest and (11) is for the lowest wake-up time. Least significant 5 bits show the probability difference of the last 8 T/NT branches, where 4 bits represent the binary equivalent of the integral value of probability difference and fifth bit is signed bit for the difference.

The next step in GA is to apply fitness function over the chromosomes to find most suitable predictor. Fitness function used in our algorithm is the number of ones in the chromosome, more the number of ones in the binary string, healthier the chromosome will be.

Probability difference of last

Type of predictor 8 TINT branches

wake-up time

Fig.2. (a) Initial Populations (b) Winner Chromosome

Further, the algorithm proceeds by setting mutation probability (0.55) and mutation point (5th bit) as shown in Figure 6 (a).

Mutation point can be a single bit or multiple bits. This process is simple, which includes flipping the bit of the chromosome on variation point.

The next stage in GA is to copy the relevant bits from winner chromosome to rest of the chromosomes, and this process is called crossover. In our chromosome strings, relevant bits are the number of ones, so we do bitwise XORing of rest of the chromosome with winner chromosome. This step helps in copying the bits containing “1” present in recipient chromosome at the crossover points to rest of the offspring.

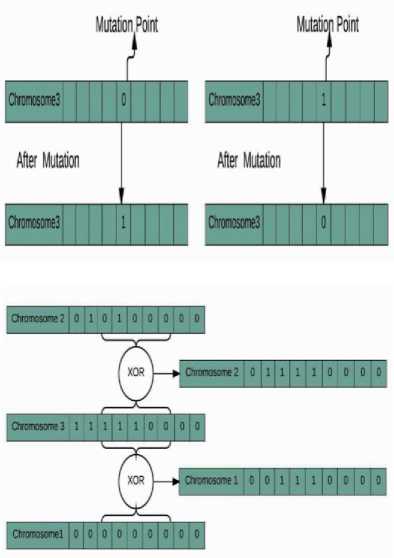
Fig.3. (a) Chromosomes before and after Mutation (b) Chromosome before and after crossover

After crossover, we get healthier generation. It can be observed from Figure 6 (b) that new chromosomal strings contain comparatively more number of ones, which means offspring of the new generation are healthier than the previous generation. This process is thus repeated in the next iteration, results in the production of new offspring from previous ones. It results in shifting to the fittest predictor, which will result in appropriate predictions every time. New population after the first iteration is shown in Figure 7.

Fig.4. Chromosome After Applying GA

Further improvement in prediction mechanism is achieved by selecting the winner chromosome along with calculating the probability of last 8 taken/Not taken branches. This probability is useful in the cases where Winner chromosome fails to predict correctly. This failure happens when the state of 2-bit counter goes wrong in such situations prediction is considered to be the one, which is more probable for e.g. If the number of taken branches are more in last eight branches then next prediction is found to be taken or vice-versa. The probability difference, which gets calculated earlier and mapped into the last 5 bits of chromosomal string, is used in this case.

• V.    Results

The designed alloyed branch predictor with Genetic algorithm simulates performance analysis on MATLAB. A 16- Instruction RISC ISA (Instruction set architecture) of a processor simulated with an instruction memory of 1MB having instruction length of 16-bits. Two branch instructions included in this ISA: Branch if Zero and branch if negative. Only the fetch stage of a processor is simulated in MATLAB with the complete proposed predictor working in the fetch stage. This simulation includes over 0.5 million instructions of which about 25% instructions are branch one. The mechanism to flip branch direction is kept random it depends upon the branch transition probabilities we set. Setting the branch transition probabilities allows us to have a controlled flow of branch instructions. High branch transition probability means a more random flipping of branches, which ultimately creates a robust environment for our predictor.

To test and compare GA with other kinds of branch predictors, we did a rigorous analysis of designed predictor on several benchmark programs. Each program has 0.5 million instructions in which more than 0.15 million instructions are branches. Statistically, every fourth instruction being a branch gives us an idea about the number of branches in a program. The branch resolving structure is kept just after the fetch stage to predict correct branch direction. The branch transition probability varies from 0.35 - 0.95 for each benchmark program. Different branch transition probabilities in every benchmark program provide randomness in forward and backward branches. It means that larger the transition probability, greater is the flipping of branch directions. Branch resolving mechanism consists of three conventional predictors with genetic algorithm applied to it. To make the comparison more extensive we did various simulations with different branch transition probabilities. Each simulation with one value of transition probability tested for various history length of 128, 256, 512, 1024, 2048 and 4096 entries.

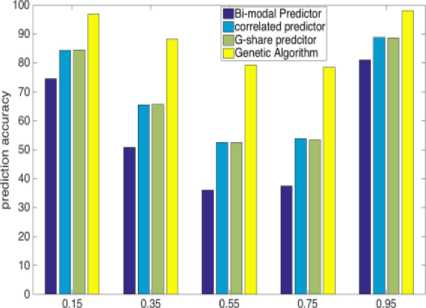
Branch transition probability (256 Entries)

Observation from tabulated as well as graphical results explains that although our prediction based on GA is not attaining high accuracy for average branch transition probabilities like 0.35 to 0.75, it’s raising with increasing history lengths and is ranging between 77%-89%. Furthermore, it is also not able to attain very high accuracy for low transition probability branches (0.15), but the prediction accuracy is consistent and near about 96%. On the other side, efficiency is as high as 98% for high transition probability branches (0.95) in significant history length. Our GA-based predictor is giving exceptional accuracy for high transition probability branches, and it is consistent for all history length.

Our predictor can choose the best predictor out of three conventional branch predictors, which includes in the structure. This decision of which predictor is fittest is critical and should be done very carefully as the selected suitable predictor is going to generate the decision bits. Our GA-based predictor is also able to make its prediction whenever the chosen conventional predictor makes a wrong move. This prediction made by GA is correct almost all the time as this decision made by calculating the branch probability differences of taken and not-taken branches executed in the past.

Branch transition probability (1024 Entries)

GA provides a considerable amount of increment in the prediction accuracies and can also perform well even if the history table is short. Moreover, we can see that during instruction fetch, branches that are usually encountered are either with very low transition probability (loop branches) or with very high transition probability (if-else branches). Higher accuracies in 0.15 and 0.95 branch transition probabilities make our branchresolving structure more suitable for the environment where branch direction is randomly flipping at a very high rate and also in the environment where it is not flipping much.

Branch transition probability (2048 Entries)

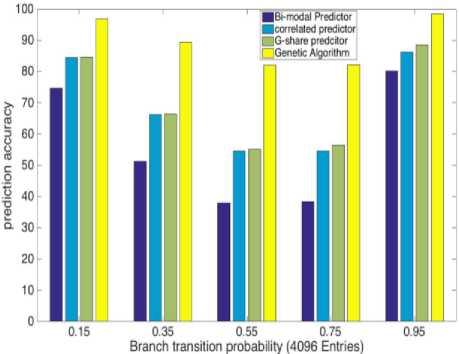
Fig.5. Prediction Accuracy for Different Predictors at Different History Length

• VI.    Conclusion

  In this paper, we systematically studied the efficiency of GA in the context of alloyed branch prediction. Our idea of applying GA in choosing fit predictor among conventional branch predictors proved to be a source of better prediction mechanism. It is evident from our results that applying GA can improve the prediction mechanism and gives a considerable amount of increment in prediction accuracy for different branch transition probabilities. This increment is more than 10% in few cases of branch transition probabilities such as 0.35, 0.55 and 0.75, whereas it’s more than 20% for 0.15 and 0.95-branch transition probabilities. Moreover, the substantial increment in accuracy can be achieved even for small history length whereas for large history length of 4096 entries; accuracy reaches as high as 98%. This makes our overall prediction mechanism more robust and reliable in conditions where branch directions are continuously flipping as seen in the case of if-else branches and also in conditions where branches are flipping at a very slow rate as seen in loop branches.