Two SAOR Iterative Formats for Solving Linear Complementarity Problems

Published Online March 2011 in MECS

For given matrix and vector, the linear complementarity problem (LCP) consists of finding a vector which satisfies the conditions z > 0, Mz + q > 0, zT (Mz + q ) = 0 (1.1)

Because the has a variety of applications such as the Nash equilibrium point of a bi-matrix game, contact problems, the free boundary problem, etc. (see [1,2]). The researches on the numerical methods for solving (1.1) have attracted much attention.

A large number of papers have studied LCP [3-14]. Numerical methods for LCP fall into two major categories: direct methods and iterative methods. In [10], several basic iterative methods to solve LCP are discussed. Recently, some new iterative methods have been proposed to solve LCP. For example, Koulisianis and Papatheodorou [14] present an improved projected successive overrelaxation (IPSOR) for the solution of an important class of linear complementarity problems. When M is a 2-cyclic matrix, Yuan and Song [15] proposed a class of modified AOR(MAOR) methods to solve it. In [16], a class of generalized AOR(GAOR) methods for solving (1.1) is introduce by applying the multi-splitting techniques. Bai [17,18] proposed a class of

This work is supported by NSF Grant #11026113 to S. Jiang.

Corresponding author: Dong-jin Yuan.

parallel iterative methods for a large linear complementarity problem.

In this paper, by applying the SAOR splitting, we propose SAOR method I and II for solving the linear complementarity problem. Convergence results for these two methods are presented when is an H-matrix (and also an M-matrix). Finally, numerical examples are given to show the efficiency of the presented methods.

We briefly introduce some essential notations. Let C = ( c i j ) _e R " ^x " be an n x n matrix, diag(C) denotes the n x n diagonal matrix coinciding in its diagonal with C. For A = ( a.. ), B = ( b ij )e R " ^x " , we write A > B if ( a i. ) > ( b i. ) holds for all i, j=1,2,...,n . Calling A nonnegative if A > 0, we say that B <  C if and only if - B > - C . These definitions carry immediately over to vectors by identifying them with n x n matrices. By |A|=(|_a ij| ) , we define the absolute value of A e R "^x" . We denote by A =( a_ij ) the comparison matrix of A e R "^x" where (a^^a jl for k=j and ^aj= - a ij for k ^ j, k, j=1,2,...,n. Spectral radius of a matrix A is denoted by p (A).

Definition 1. Let A = (a, j) e R"x" . It is called (1) L-matrix if akk > 0, k = 1,2,K , n, and akj < 0, k Ф j, k, j = 1,2,K, n;

• (2)    M-matrix if it is a nonsingular L-matrix satisfying A ^{- 1} > 0;

• (3)    S- matrix if 3 x >  0, Ax >  0

• (4)    H-matrix if { A ) is an M-matrix.

• (5)    H ₊ -matrix if A is an H-matrix and a kk >  0, k = 1,2, K , n . Definition 2. For A = ( _a i. ) _e R " ^x " , vector _{x +} is defined such that ( x+') = max { 0, x j , j = 1,2, K , n . Then for any _x , y _e Rⁿ , the following facts hold in [19]

• ⁽¹⁾    ( ^{x +} У ) ₊<  ^x + ⁺ У + ^;

• (2)    x + ^- y + < ( x ^- y ) ₊ ;

(3)1 x = x + ⁺(^- x ) + ;

• ⁽⁴⁾    x <  y ^ x ₊ <  y ₊ .

Lemma 1.1 [20] Let A = M - N be an M-splitting, then p ( M ¹ N ) < 1 о A is a nonsingular M-matrix.

Lemma 1.2 [21] Let M H ₊ -matrix, then LCP (M,q) has a unique solution z e Rⁿ .

Lemma 1.3 [22] A is an M-matrix if and only if A is a Z-matrix and an S-matrix.

Lemma 1.4 [23] Let A is an M-matrix, D 1 = diag ( A 1 ), C 1 = D 1 - A 1 . If D 2 > 0 _e R^{n x n} is a diagonally matrix and C ₂ e R n ^x n , 0 <  C ₂<  C , , then A = ( D 1 - D 2 ) -( C 1 - C ₂) and A ^{- 1} <  A 1 ^{- 1}

• II.    SAOR M ETHOD F OR LCP( M , Q )

Let where M = D - B = D-L-U , D = diag ( M ) = ( d j ) , L = ( l j ) , and и = ( j , i ; j = 1,2,3,... n are diagonal, strictly lower and upper triangular matrices obtained from M, respectively. It has been shown in [24,25] that z ^* solves LCP (M,q) (1.1) if and only if it satisfies

Z* = (Z* - D (MZ+q))+ where D = diag(M).

Now we propose two new iterative methods for solving LCP (M,q) (1.1) as follows.

Format I (SAOR method)

Step 1: Choose an initial vector z ⁰ e Rⁿ and a parameter ® , r e R ⁺ , set k = 0;

Step 2: Calculate zk+1 = (zk - D- {- /Lzk+1 + [to (2 - to)M + yL] zk

+ to ( 2 - to ) q }) +

Step 3: If z^{k + 1} = z^k , then stop; Else set k = k +1 and go to step2.

Format II (SAOR method)

Step 1: Choose an initial vector z ⁰ e Rⁿ and a parameter to , r e R ⁺ , set k = 0;

Step 2: Calculate zk+1 = (zk - D-1 {- /Uzk+1 + [to(2 - to ) M + /U ] zk

+ to ( 2 - to ) q }) +

Step 3: If z^{k + 1} = z^k , then stop; Else set k = k + 1 and go to step2.

Remark

• (1)    If M is a symmetric matrix, then method I and II coincide;

• (2)    If _to = у , then SAOR method reduces to SSOR method;

• (3)    If to = 1, then SAOR method reduces to AOR method; (4) If _to = у = 1, then SAOR method reduces to SOR method.

• III.    C onvergence A nalysis F or h ₊ -M atrix

At first we define the operator f _: R n ^ R n in accordance with the rule: f ( _z ) = § , where § is the fixed point of the system of equations

• § = ( z - D ¹ { - yL§ + [ to ( 2 - to ) M + yL ] z + to ( 2 - to ) q } )

(3.1)

and g _: R n ^ R n such that g ( _z ) = n, where ^ is the fixed point of the following system of equations

П = ( z - D ^{- 1} { yUn + [ to ( 2 - to ) M + yU ] z + to ( 2 - to ) q } )

(3.2) we can prove the following convergence theorem for the SAOR method.

Theorem 3.1. Let M = D - B = D - L - U be an H ₊ -matrix and D = diag ( M ) , L , U be diagonal, strictly lower and upper triangular matrices obtained from M, respectively. If 0 <  y <  _to < 1, then for any initial vector z ⁰, Method I and II converge to the unique solution of LCP (M,q).

Proof. First we consider the sequence {zk} generated by Method I. By Lemma 1.2, LCP(M,q) has a unique solution z* e Rn, that is f (z * ) = z * •

Suppose that n = f (y), i.e.,

П = ( y - D ^{- 1} { - YLn + [ to ( 2 - to ) M + yL ] y + to ( 2 - to ) q } )

(3.3)

Then by subtracting (3.3) from (3.1), we get

§-П = ( z - D ^{- 1} { - yL§ + [ to ( 2 - to ) M + yL ] z + to ( 2 - to ) q } )

- ( y - D ¹ { -YLn + [ to ( 2- to ) M + yL ] y + to ( 2 - to ) q } )

< ( ( z - y ) - D ¹ { - yL§ + [ to ( 2 - to ) M + yL ] ( z - y ) } )

= ( yD ¹ L ( §-n ) + ( { I - D ¹ [ to ( 2 - to ) M + yL ] } ( z - y ) ) )

So we can get

⁽ § ^- n ) + < ( YD ^{- L (} § ^- П ) )₊

+ ( ( I - D ^- [ to ( 2 - to ) M + yL ] ) ( z - y ) ) +

(3.4)

Analogously, we can obtain

( n - § )₊ < ( YD ^{- 1} L ( n - § ) ) ₊ + ( ( I - D ^{- 1} [ to ( 2- to ) M + yL ] ) ( y - z ) ) +

(3.5)

Now, the combination of (3.4) and (3.5) directly give the following estimates

I § ^{- n} = ( § ^- n )₊ ⁺ ( n ^- § )₊

< ( yD ^{- 1} L ( § - n ) )₊ + ( yD ^{- 1} L ( n - § ) )₊

+ ( ( I - D ¹ [ to ( 2 - to ) M + yL ] ) ( z - y ) )

+ ( ( I - D ¹ [ to ( 2 - to ) M + yL ] ) ( y - z ) )

= \yd "1 L ( 5 - n )| + |( I — D "1 [ w ( 2 — ® ) M + YL ] ) ( z - У ) <  yD-¹ | L ||( f - n )| + |( I — D "1 [ ^ ( 2 — ® ) M + YL ] ) | z — У| i.e.,

( I - y D "* | L |) 5"A <| I - D ^- [ ® ( ² - ® ) M + YL ]I z - У , let

Q = I - yd ¹ | L , R =| I - D "’ [ to (2 - to ) M + yL ].

Then, we can get

1 5 - n <  Q "* R|z - y ■                           ⁽³-⁶⁾

According to the definition of Method I and (3.6), we can get

I z^{k +} - z *| =| f ( z k - z • )| < Q- R|z^k - z * ■

According to Lemma 1.2, It is easy to see that the iterative sequence { _z ^k } , k = 0,1,2, K generated by Method I converges to the unique solution z * if p ( M ^{- 1} N ) < 1 ■

Let T = Q - R, then we know that Q = I - yD |l| is an M-matrix, and R = |i - D-1 [0 (2 - to) M + yL]| > 0, and since 0 < у < to<1, so T = Q - R > to(2 - to) D-* (D-|B|) @ T, since M is an H+ -matrix, so D - 1B = M   is an M-matrix, then for any0 < y < to < 1,3 x > 0 such that

TX = to ( 2 - to ) D -¹ ( D -| B |) x > 0,

Therefore, T ^∞ is an M-matrix.

Since T is a Z-matrix and T >  T , according to Lemma 1.4, It is easy to see that T is an M-matrix, i.e., T ^- > 0 ■

In addition, T is nonsingular and T = Q - R is M-splitting, according to Lemma 1.1, T ^- > 0 о p ( Q ^- R ) < 1. Hence p ( Q ^- R ) < 1.

Similarly, we can obtain the above results if we consider the sequence { _z ^k } generated by Method II. W

Corollary 3.2. Let M = D - B = D - L - U be an M-matrix and D = diag ( M ) , L , U be diagonal, strictly lower and upper triangular matrices obtained from M. If 0 <  y <  _to < 2 , then for any initial vector z ⁰ , Method I and II converge to the unique solution of LCP (M,q).

Proof. First we consider the sequence { z k } generated by Method I. By Lemma 1.2, LCP (M,q) has a unique solution z * e R " , that is ^{f ( z} * ) = ^z * .

Suppose that n = f ( y ) , i.e.,

П = ( y - D ^{- 1} { - yLn +[ to ( 2- to ) M + yL ] У + to ( 2- to ) ^ } )     ⁽3.⁷⁾

Then by subtracting (3.3) from (3.1), we get

5 - n = ( z - D ^{- 1} { - yL5 + [ to ( 2 - to ) M + yL ] z + to ( 2 - to ) g } )

- ( y - D ^- { -YLn + [ to ( 2 - to ) M + yL ] y + to ( 2 - to ) ^ } )

< ( ( z - y ) - D ¹

{ -YL5 + [ to ( 2 - to ) M + yL ] ( z - y ) } )

= ( yD ¹ L ( 5 - n ) + ( { I - D ¹ [ to ( 2 - to ) M + yL ] } ( z - y ) ) )

So, we can get

^{( 5-} n ) + < ( YD ^{- L ( 5-} n ) )₊

+ ( ( I - D ^- [ to ( 2 - to ) M + yL ] ) ( z - y ) ) +

(3.8)

Analogously, we can obtain

( n - 5 )₊ < ( YD ^- L ( n - 5 ) ) ₊ + ( ( I - D "¹ [ to ( 2- to ) M + yL ] ) ( y - z ) ) +

(3.9)

Now, the combination of (3.8) and (3.9) directly gives the following estimates

1 ^{5 - n} = ^{( 5 -} n ) + ^{+ (} n ^{- 5} ) +

< ( YD ^- L ( 5 - n ) )₊ + ( YD ^- L ( n - 5 ) )₊

+ ( ( I - D ^- [ to ( 2 - to ) M + yL ] ) ( z - y ) )

+ ( ( I - D ^- [ to ( 2 - to ) M + yL ] ) ( y - z ) )

= \yD-¹ L(5 - n )| + |( I - D -¹ [ to ( 2 - to ) M + yL ] ) ( z - y )

< yD"1 L||(5 - n) +1(I - D"1 [to(2 - to)M + yL])||z - y| ei’-yD-1L) 5-n <| I - D-1 [to( 2-to) M+yL ] |z - y, let

Q = I - yD "* | l| , R = | i - D -¹ [ to ( 2 - to ) M + yL ]|.

Then, we can get

1 5 - n <  Q "1 R|z - y .                      ⁽3.¹⁰⁾

According to the definition of Method I and (3.10), we can get

I zk+ - z *| =| f (zk - z • )|< Q-1 R|zk - z *.

According to Lemma 1.2, It is easy to see that the iterative sequence { z^k } , k = 0,1, 2, K generated by Method

I converges to the unique solution z * if p ( M ^- N ) < 1.

Let T = Q - R, then we know that Q = i - ^D|l| is an M-matrix, and R = |i - D- [to( 2 - to) M + yL ]|> 0, and since 0 < y < to < 2, so T = Q - R > to(2 - to) D-* (D-|B|) @ T, since M is an H+ -matrix, so D- I Bl = M is an M-matrix, then for any0 < y < to < 2,

3 x > 0 such that TX = to ( 2 - to ) D "* ( D -| B |) x > 0,

Therefore, T ^∞ is an M-matrix.

Since T is a Z-matrix and T > T , according to Lemma 1.4, It is easy to see that T is an M-matrix, i.e., T ^- >  0 .

In addition, T is nonsingular and T = Q - R is M-splitting, according to Lemma 1.1, T ^- > 0 о p ( Q ^- R ) < 1.

Hence p ( Q -1 R ) < 1.

Similarly, we can obtain the above results if we consider the sequence { z k } generated by Method II. W

• IV.    M ONOTONE C ONVERGENCE A NALYSIS

In this section, we mainly discuss the monotone convergence properties of the SAOR methods, when the system matrix M e R n ^x n is an L-matrix. First, we define the following set

A = { x e Rn |x > 0, Mx + q > 0 }

Obviously if LCP(M,q) is solvable, then the set A is nonempty.

Theorem 4.1. Let the operator f : R n ^ R n be defined in (3.1). Suppose that M e R n ^{x n} is an L-matrix, and also 0 <  y <  ° < 1. Then for any z e A , it holds that ⁽¹⁾ f ( z ) < z ;

• ⁽²⁾    y <  z ^ ^f ( y ) < ^f ( z ) ;

• ⁽³⁾    5 = f ( z ) eA .

• 5.< z_t, i = 1,2, K n                         (4.1)

Proof: We firstly verify (1) We only need to show that

where f                              .-1                                                                                A

5 = 1 z - d; ^{x -} y S 4(^ j - ^zj ) ⁺ ° ( ²- ° )( ^{Mz +} q X I

I L j =i                                          JJ +

(4.2)

We use induction on i to prove (4.1). When i = 1, noticing that M is an L-matrix, 0 <  y <  ° < 1 and z e A , z 1 > 0, ^and d i ^{- 1} L ° ( 2 - о )( Mz + q ). ] > 0 , ^{thus 5} = ( z ^- d"^{1 L} ° ( 2^- ° )( Mz ⁺ q ) . ] ) + <  z y

Now assume that (4.1) holds for vi < k (0 < k < n), then we get zk+1 > 0, and      -1

^dk +1 k +1

k

^- y S L ⁽ 5 ^- z j ⁾⁺ ° ^{(2 -} ° ⁾⁽ Mz ⁺ q ) k +1

j =1

> 0

Thus

’k +1

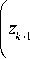
d uk+1 k+1

k

^- y S L j ^{5 -} z j -W ^{2 -} ° ⁾⁽ Mz ⁺ q ) k +1

j =1

J <  z +i '+

By the principle of induction, (4.1) holds for all i = 1,2,...,n.

To verify (2), we denote n = f ( y ) , where n is the fixed point of the system of equation

П = ( y - D ¹ { -yLn + L ° ( 2 - ° ) M + YL ] У + ° ( 2 - ° ) q } )

Now we only need to show that pi < 5, when y < z , j = 1,2,K, n(4.3)

by noticing (4.2) we can obtain i-1

5 = (z. - d [-YS Ln5; + YS Ljzj + °(2 - °) d z j=1

i-1

- ° (2 - °) S Ljzj+° (2 - °) S Uz j=1

= ((°-1)2z -^"’[-YSL 5 +(°2 -2°+Y)SLjzj j=1

• ^- ° ( ^{2 -} ° ) S ^Uj^zj ⁺ ° ( ^{2 -} ° ) q ^]) +

j = i +1

(4.4) and

• n . = ⁽⁽ ° ^-1)2 У ^{- d [-} Y S Ln ⁺ ( ° ^{2 -} 2° ⁺ Y ) S L j y j

j =1                                       j =1

• ^- ° ( ^{2 -} ° ) S ^U_ljy_j ⁺ ° ( ^{2 -} ° ) q i ^]) +

j = . +1

Considering the hypotheses y < z , then when i = 1, we obtain

51 = ((° -1)2 z1 + dn-1[°( 2 - °) S^ U jzj - °(2 - °) q1])+ j =2

• >⁽⁽ ° ^-1)2 y 1 ^{+ d} 11 ^{- 1[} ° ( ^{2 -} ° )Sl ^UцУ ; ^- ° ( ^{2 -} ° ) q 1 ^]) + = П 1

• 4 . +1 <  5 k +1 .

j =2

Now assume that (4.1) holds for v i < k (0 < k < n), when i = k + 1, by (4.3), (4.4) and y < z and hence,

Hence the conclusion (4.3) holds by the principle of induction.

Now, we turn to (3).

Let z = f (5),5 = f (z) , by (1) we immediately get f (5)<5, so Z<5.

By the definition of operator f we see that

Z = f ( 5 ) > 0, 5 = f ( z ) > 0,

Now by induction, we prove

( M5 + q ) j > 0, j = 1,2,..., n

Obviously ( M5 + q ) 1 > 0,

Otherwise, Z 1 = ( 5 1 - d _n ^{- 1} ° ( 2- ° )( MZ + q ) 1 ) + > ( 5 1 ) + = 5 1 .

This contracts Z <  5 .

Now, we assume that ( m ^ + q ) j >0 , j = 1,2,..., k -1.

Since z j < 5 j , j = 1,2,..., k -1 , we can obtain

( M5 + q ) k >0.

Otherwise, by defining и = ( 5 - ° ( 2 - ° ) D ^{- 1} ( M5 + q ) ) , we obtain _{U k} >  5 _k , On the other hand, the following estimates can by straightforwardly deduced from the definitions of ^ and и , k - 1

Zk = (5k - dkk+ [-YS Lkj (Zj - 5j) + °(2 - °) (Mz + q)k ])+ j=1 k-1

= {L1 - °(2 - °)] 5k + dkk-1YS LkjZj - Ydkk-1 S Lkj5j + j=1

k-1

° ( 2 - ° ) d kk ^- 1 S L kj Z j + ° ( 2 - ° ) d kk ^- 1 Y S U kj 5 j } + j =1                                            j = i +1

+ ° ( 2 - ° )( Mz + q ) . ]) +

k -1

k -1

< {(1 - to )2 §k + Ydkk-1 £ j - Ydkk-1 £ j j =1

n

j =1

k -1

+ to(2 - to)dkk-1 E j + to(2 - to)dkk-1Y E Uk^j}+ j =1

k -1

j = i +1

n

= 1 ( 1- to ) ² Z k + to ( 2- to ) d kk ^-1 E j + to ( 2- to ) d kk ^{- 1} E j

I                               j =1                         j =+1

= ( ^Z k ^{- to} ( ^{2 - to} ) d kk ^{- 1} ( MZ ⁺ q ) k )₊ = ". .

i-e-, Z k <  U k -

In addition, since

+

Z - v = ( Z - D ¹ { [- YLZ + to ( 2 - to ) M + yL ] Z + to ( 2 - to ) q } )

- ( Z - to ( 2 - to ) D ^- ( MZ + q ) ) +

<( Y D-1L(Z - Z))+ and analogously, u-Z<(YD-1L(Z-Z)) ’

|Z - U = ( Z - u ) + + ( u - Z ) + < ( y d ^{- 1}l ( Z - Z ) ) + + ( y d ^{- 1}l ( Z - Z ) ) +

=| y D ^{- 1}l ( Z - Z )| <  ? d | L Z - Z = Y D^-1L Z - Z

< Yto ( 2 - to ) D "* L ( I - yD "* L ) ^-1 D "* MZ + q | ^ 0 ( у ^ 0 )

that is, li_m z = v

Y ^0

Here, the estimate

I Z - Z <  to ( 2 - to ) ( I - yD "* L )^{- 1} D "* I MZ + q

(4.5)

is used. In fact, with the facts of Definition 2 we have f (Z) = Z=(Z-D-1 {-yLZ+[to( 2 - to) M+yL ]Z+to( 2 - to) q})+

< Z++(-D-1 {-yLZ + [to(2 - to)M + yL] Z + to(2 - to) q}) and f (Z) = Z = (Z - D- {-yLZ+[to(2-to) M+yL ] Z+to( 2 - to) q})+ > Z+ - (D-1 {-yLZ + [to (2 - to)M + yL] Z + to (2 - to) Z}) . So, we obtain

( Z - Z ) + <  ( YD ^{- 1} L ( Z - Z ) - to ( 2 - to ) D ^{- 1} ( MZ + q ) ) +

( Z - Z ) + <  ( - YD ^{- 1} L ( Z - Z ) + to ( 2 - to ) D ^{- 1} ( MZ + q ) ) + • Therefore,

| Z - Z= ( Z - Z ) + + ( Z - Z ) +

< |y D -¹ L ( Z - Z ) - to ( 2 - to ) D -¹ ( MZ + q )|

• < yD "* L Z - Z - to ( 2 - to ) D -¹ | MZ + q|

i.e.,

IZ - Z < to(2 - to)(I - yD L) |MZ + q\, thus, (4.5) holds.

Moreover, observing u k >  Z _k , So we get Z _k <  _{u k} and lim Z = и . We know that Z _k <  Z _k must hold for some Y ^0

sufficiently small y _e [ 0,1 ] .

However, this contracts Z <  Z .

Therefore, ( MZ + q ) _k >  0 .

By induction, we obtain Z_eA . W

Theorem 4.2. Let the operator g : R n ^ R n be defined in (3.2). Suppose that M e R n ^x n is an L-matrix, and also 0 <  y <  to < 1. Then for any z e A , it holds that ⁽¹⁾ g ( z ) < z ;

• ⁽²⁾    y <  z ^ g ( y ) < g ( z ) ;

• ⁽³⁾    П = g ( z ) e A .

Theorem 4.3. Suppose that M e Rnxn is an L-matrix, and also 0 < y < to < 1, then for any initial vector z0 e A, the iterative sequence {zk} generated by Methods I and II has the following properties

•^{k + 1}<  z^k <  z 0 , k = 0,1,2, K

• (1)    0 <  z

• (2)    li_{m z} k ^x

k

= _z * , z * is the unique solution of the LCP(M,q).

Proof. We only give the proof for the SAOR Method I.

Since z0 e A, by (a) of Theorem 4.1 we have f (z0 ) = z1 < z0 and z1 e A.

Now, using (a) of Theorem 4.1 again, by recursively we have shown the validity of (a).

The inequalities given in (1) show that the sequence { _z ^k } is monotone bounded, so that it converges to some vector z ^* satisfying

z * = ( z * - D ^{- 1} { - yLz * + [ to ( 2 - to ) M + yL ] z *

⁺ о ( ^{2 - to} ) q ^}) +

= ( z * - D ^{- 1} [ to ( 2 - to ) Mz * + to ( 2 - to ) q ] )

Hence, z ^* is the unique solution of the LCP (M,q).

Theorem 4.4. Let M e Rnxn be an L-matrix. Then for any initial vector z0 = y0 e A , both the iterative sequences {zk} and {yk} generated by the SAOR Method I (or SAOR Methods II) corresponding to the parameter (to, y) and (to, y ) respectively, converge to the solution z* of the LCP(M,q) and it holds zk < y, k=0,1,2,K ,

(4.6)

provided the parameter ( _to , у ) and ( _to , у ) satisfy

0 <  to <  to < 1; 0 <  y <  Y < 1; 0 <  Y <  to <  1 ; 0 <  Y <  to < 1.

Proof. The convergence of sequences { _z ^k } and { y^k } is proved by Theorem 4.3.

Now, we prove (4.6).

First we define the operator f : R n ^ R n such that Z = f (z), where Z is the fixed point of the following system

Z = ( z - D ^{- 1} { - yLZ + [ to ( 2 - to ) M + yL ] z

+ to ( 2 - to ) q }) +

Since yp+1 = (yp - D-1 {-yLyp+1 + [0(2 - to) M + yL] yp

^{+ 0} ( 2 ^- to ) q }) ₊

In addition, since

• - yLy p ^{+ 1} + 0 ( 2 - ® ) M + yL ] y p + 0 ( 2 - 0 ) q

= -YLy^{p + 1} -+ 0 ( 2 - 0 ) M + yL ] + 0 2- 0 ) q

• <-YL ( y^{p + 1} - y^p ) + 0 ( 2 - 0 ) ( My^p + q )

Therefore, yp+1 > (yp - D-1[ - yL (yp+1 - yp)

(4.7)

^{+ 0} ( 2 ^{- 0} ) ( My p + q ) ^]) + = f ( y^p )

We verify (4.6) by induction. In fact, when k= 0, the inequality (4.7) is trivial. Suppose that (4.6) holds for some positive integer p.

z k <  y k , k = 0,1,2, K p .

Then, by Theorem 4.1 and the inequality (4.7), we get

Z p ^{+ 1} = f ( z p ) < f ( y^p ) < y^{p + 1}

and hence z k <  y k , k = 0,1,2, K .

This completes the proof. W

Remark . Theorem 4.4 shows that suitable increase of the parameter 0 can accelerate the convergence rate of Methods I and II. Furthermore, the parameter у = ₀ =1 can result in the fastest convergence rate of Methods I and II under the restrictions made in Theorem 4.4. Moreover, Theorem 4.4 implies that the optimal parameter in general should be ₀ , Y e [1, да).

V. N UMERICAL R ESULTS

In this section, we present numerical results to show the efficiency and robustness of SAOR methods and AOR method for different cases. The codes are written by Matlab.

Example 5.1. We consider the LCP(M,q) with

M =

( S O

O M ^M

M

I O

- 1

S O M

M M O

- 1

- 1

S

O

- 1

- 1

L

L

L

O

O

O

L

L

O

S

O

O )

O

O

M

^{- 1}

^{- 1}

S J

e R

) n x n

, q =

r

- 1

- 1

M

1 \ n -1

e Rⁿ ,

I (- 1 )" J

where S = tridiag (1,8, -1) e R ^x n , I e R ^x n is the identity matrix, and n ² = n . It is known that M is a strictly diagonally dominant matrix and thus is an H-matrix. So the LCP(M,q) has a unique solution z ^* e Rⁿ as all diagonal elements of M are positive.

For the test problem, we take the initial vector z ⁰ = ( 5,5, L ,5 ) T . The termination criterion for the

iterative methods is ^ ( _z ^k ) = || _z ^k

_z ^{k - 1}1| < 10 ^{- 6}, and let NI

and CT denote the number of iterations and CPU time, respectively.

TABLE I

T HE NUMBER OF ITERATIONS AND CPU TIME OF S AOR METHODS AND

A or method with DIFFERENT 0 AND y

SAOR Method I				SAOR Method II		AOR Method
CT     NI				CT     NI		CT     NI
n =100
0 = 0.02	Y = 0.01	0.090985	94	0.325161	338	0.190866	186
	Y = 0.02	0.090866	94	0.325073	338	0.184414	186
0 = 0. 2	Y = 0.1	0.010501	11	0.030769	32	0.018416	19
	Y = 0.2	0.011828	11	0.030896	32	0.018500	19
0 = 1.0	Y = 0.5	0.002886	3	0.002934	3	0.002884	3
	Y = 1.0	0.002877	3	0.001954	2	0.002933	3
0 = 1.2	Y = 1.1	0.002902	3	0.005775	6	0.002938	3
	Y = 1.2	0.003183	3	0.005795	6	0.002871	3
0 = 1.5	Y = 1.4	0.004843	5	0.011555	12	0.002872	3
	Y = 1.5	0.004787	5	0.012199	12	0.003197	3
0 = 1.9	Y = 1.8	0.024374	19	0.048328	50	0.002950	3
	Y = 1.9	0.019261	19	0.051670	50	0.002874	3
n =400
0 = 0.02	Y = 0.01	1.506276	94	5.341039	338	3.028217	186
	Y = 0.02	1.502442	94	5.366817	338	2.971320	186
0 = 0. 2	Y = 0.1	0.179784	11	0.508014	32	0.313488	19
	Y = 0.2	0.175714	11	0.506876	32	0.303919	19
0 = 1.0	Y = 0.5	0.047926	3	0.048960	3	0.050338	3
	Y = 1.0	0.048211	3	0.032247	2	0.051095	3
0 = 1.2	Y = 1.1	0.048373	3	0.095202	6	0.049685	3
	Y = 1.2	0.079654	3	0.097641	6	0.050580	3
0 = 1.5	Y = 1.4	0.080009	5	0.192267	12	0.050817	3
	Y = 1.5	0.004787	5	0.190988	12	0.049053	3
0 = 1.9	Y = 1.8	0.303809	19	0.804721	50	0.048557	3
	Y = 1.9	0.300135	19	0.804678	50	0.047645	3
n =900
0 = 0.02	Y = 0.01	1.508788	94	28.414443	338	15.953723	186
	Y = 0.02	1.510670	94	28.391582	338	15.788688	186
0 = 0. 2	Y = 0.1	0.173260	11	2.701051	32	1.635054	19
	Y = 0.2	0.18362	11	2.696842	32	1.615800	19
0 = 1.0	Y = 0.5	0.048242	3	0.255264	3	0.261636	3
	Y = 1.0	0.047447	3	0.173271	2	0.255026	3
0 = 1.2	Y = 1.1	0.048009	3	0.511831	6	0.253369	3
	Y = 1.2	0.048526	3	0.509011	6	0.254806	3
0 = 1.5	Y = 1.4	0.080753	5	1.016569	12	0.252666	3
	Y = 1.5	0.078928	5	1.026680	12	0.256678	3
0 = 1.9	Y = 1.8	0.299969	19	4.211614	50	0.254958	3
	Y = 1.9	0.303658	19	4.224083	50	0.253611	3

In above Table, we report the number of iterations (NI) and the CPU time (CT) for SAOR Method I ,II and the AOR method with several values of _n , ₀ and y . We can easily see that SAOR method I is more efficient than the AOR method when 0 <  y <  ₀ <1 ; while when 1 <  y <  ₀ < 2 , AOR method is more efficient than the SAOR methods. Furthermore, it can be observed that the iterative methods are more efficient (require less number of iterations and less CPU time) for ₀ = y = 1 than for any other values of 1< y <  ₀ < 2. The obtained results confirm Theorem 4.4.

Example 5.2. We consider the LCP(M,q) with

	f S	- I	- I	O	L	O	O ^
	- I	S	- I	- I	L	O	O
	I	- I	S	- I	L	O	O
M =	M	M	O	O	O	O	M	е R n " n , q = 1 x
								2
	M	M	O	O	O	O	- I
	M	M		O	O	S	- I
	. O	O	L	L	I	- I	S 2

-1

-1

M

л

(-1)

I (-1) n J

е R n ,

where S = tridiag(-1,8,-1) е Rnxn, I е Rnxn is the identity matrix, and n2 = n . It is known that M is a strictly diagonally dominant matrix and thus is an H-matrix. So the LCP(M,q) has a unique solution z* е Rn as all diagonal elements of M are positive.

For the test problem, we take the initial vector z0 = (1,1,L ,1)T. The termination criterion for the iterative methods is g(zk ) = ||zk denote the number respectively.

_z k ^{- 1}|| < 10 ^{- 6}, and let NI and CT

of iterations and CPU time,

TABLE II

T HE NUMBER OF ITERATIONS AND CPU TIME OF S AOR METHODS AND

A or method WITH DIFFERENT О AND y

SAOR Method I				SAOR Method II		AOR Method
CT     NI				CT     NI		CT     NI
П =1600
о = 0.02	Y = 0.01	20.308385	73	94.069541	342	10.955102	39
	Y = 0.02	20.270827	73	94.120451	342	10.900430	39
о = 0. 2	Y = 0.1	2.496932	9	8.636219	31	4.351129	14
	Y = 0.2	2.509314	9	8.569687	31	4.032793	14
о = 1.0	Y = 0.5	0.835130	3	0.829711	3	0.870821	3
	Y = 1.0	0.830487	3	0.552401	2	0.864844	3
о = 1.2	Y = 1.1	1.109869	4	1.398553	5	0.871275	3
	Y = 1.2	1.111170	4	1.366872	5	0.866501	3
о = 1.5	Y = 1.4	1.384278	5	2.762510	10	0.865004	3
	Y = 1.5	1.389940	5	2.769446	10	0.862292	3
О = 1.9	Y = 1.8	4.988587	17	18.405688	66	0.860734	3
	Y = 1.9	5.008520	18	18.402788	66	0.875587	3
П =2500
О = 0.02	Y = 0.01	50.198872	73	239.820921	342	27.710389	39
	Y = 0.02	51.065257	73	242.195822	342	27.895996	39
О = 0. 2	Y = 0.1	6.169381	9	22.799026	31	10.086184	14
	Y = 0.2	6.215158	9	21.711305	31	9.961821	14
О = 1.0	Y = 0.5	2.099304	3	2.116012	3	2.131103	3
	Y = 1.0	2.096300	3	1.4089942	2	2.086115	3
О = 1.2	Y = 1.1	2.850256	4	3.568269	5	2.147736	3
	Y = 1.2	2.852591	4	3.565971	5	2.191557	3
О = 1.5	Y = 1.4	3.487906	5	7.451265	10	2.091660	3
	Y = 1.5	3.484476	5	7.104976	10	2.108486	3
О = 1.9	Y = 1.8	11.863004	17	46..944535	66	2.085043	3
	Y = 1.9	13.032742	18	47..311643	66	2.183462	3

In Table II, we report the number of iterations (NI) and the CPU time (CT) for SAOR Method I ,II and the AOR method with several values of _n , _О and y. We can easily see that SAOR method I is more efficient than the AOR method when 0 <  у <  _О < 1; while when 1 <  у <  _О<  2, AOR method is more efficient than the SAOR methods. Furthermore, it can be observed that the iterative methods are more efficient (require less number of iterations and less time) for _О = у = 1 than for any other values of

1< у <  to< 2. The obtained results confirm Theorem 4.4 again.

• VI. Conclusion

In this paper, we have proposed two new iterative SAOR methods for solving the linear complementarity problem. Then, some sufficient conditions for convergence of two new iterative methods have been presented, when the system matrix M is an M-matrix. Moreover, we have discussed the monotone convergence of the new methods when M is an L-matrix. Lastly, we have reported the numerical results of our proposed methods for their robustness and efficiency.