Учебно-исследовательский стенд типа «трипод» с параллельной кинематикой и компьютерным управлением

Стенд типа «трипод» предназначен для исследования, программирования и наладки роботов, измерительных машин, динамических платформ и других устройств с параллельной кинематикой типа «трипод». Стенд имеет настольное исполнение и крепится на металлической раме, причем он может работать в перевернутом на 180° положении, система управления интегрирована в раму стенда (рис. 1). Компьютерная система управления имеет 2 режима работы – режим имитатора и режим отработки управляющей программы реальным триподом. Каждый режим имеет 2 формы интерфейса – сокращенную («имитатор») и расширенную («управляющая программа»). Принципиальное отличие режимов работы программы в этих режимах заключается в том, что имитатор управляет виртуальной моделью, а режим «управляющая программа» управляет реальной физической моделью трипода.

Переключение между режимами осуществляется постановкой или снятием галочки в

Рис. 1. Трипод

поле «Имитатор», расположенном верхней части окна (рис. 2). Функциональность этих форматов отличается лишь только возможностью настройки, а также визуализацией трипода.

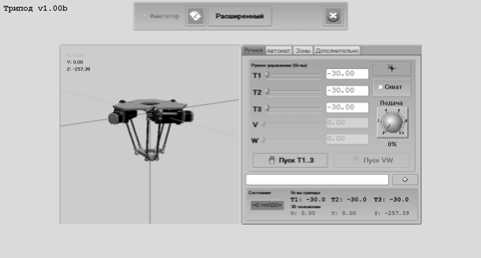
Рис. 2. Интерфейс программы

В расширенном формате есть возможность дополнительной настройки системы, просмотра информации и просмотра управляющей программы (УП). В сокращенном формате есть окно визуализации положения трипода в пространстве и расположения каждого из звеньев. В сокращенном формате в левом окне имеется четыре вкладки – «Ручное», «Автомат», «Зоны» «Дополнительно». Из вкладки «Ручное» можно управлять триподом вручную. Перемещение звеньев трипода осуществляется перетаскиванием бегунков по шкале (влево или вправо). Бегунки по осям Т1, Т2, Т3 перемещаются с помощью мыши. Оси V,W в данном программном обеспечении неактивны. В поле расположенном справа от шкалы будет отображаться соответствующее численное значение перемещения. Повороты вокруг осей Т1, Т2, Т3 измеряются в градусах. Выход в координаты Т1, Т2, Т3 может выполняться как последовательно, так и с одновременным управлением и интерполяцией по 3 координатам. Команда вывода трипода в нулевое положение обнуляет все координаты и выводит трипод в аппаратный ноль. В окне состояния отображаются фактические координаты трипода, а также фактические углы его звеньев. Из окна автоматического управления можно управлять только посредством УП. Формирование программы можно провести в режиме ручного управления, а также в автоматизированном режиме путем записи истории команд в отдельный файл. Вкладка «Зоны» визуализирует рабочую зону трипода (рис. 3). На графике моделируется область, в которой трипод может занимать любое положение. Реально рабочая зона трипода представляет из себя 3-х мерную фигуру (цилиндр), но поскольку любая из проекций на плоскость одинакова, то для визуализации достаточно плоской фигуры. Вертикальными линиями на графике обозначена программная зона ограничения перемещений, настройка зоны ограничений задается при наладке указанием радиуса (в данном случае R=198 мм).

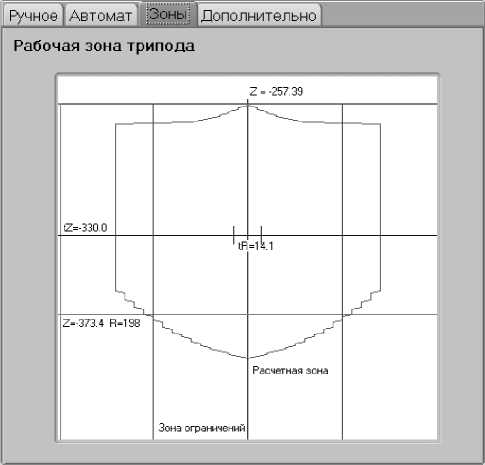
Рис. 3. Вкладка «Рабочие зоны трипода»

Математический аппарат для моделирования положений звеньев трипода реализован в Mathlab. Для решения прямой задачи механики робота, зная положение звеньев расположенных на приводах (углы theta 1, theta 2, theta 3), можно определить в декартовых координатах положение рабочего органа манипулятора (рабочей площадки) (рис. 4). Фактическое положение движущегося треугольника показывается горизонтальной линией, отмеченной параметром tZ (в данном случае tZ=-330,0 мм), это расстояние между плоскостями основного и движущегося треугольника. Короткие вертикальные линии, находящиеся на одинаковом расстоянии от оси Z, определяют ось движущегося треугольника и показывают радиус между осью Z и осью движущегося треугольника. Это расстояние обозначается параметром tR (в данном примере tR=14,1 мм). Достаточно ввести несколько параметров ограничений (минимальная и максимальная координаты Z, скорость подачи и число точек

(кадров УП) и компьютер сам сформирует управляющую программу движения трипода.

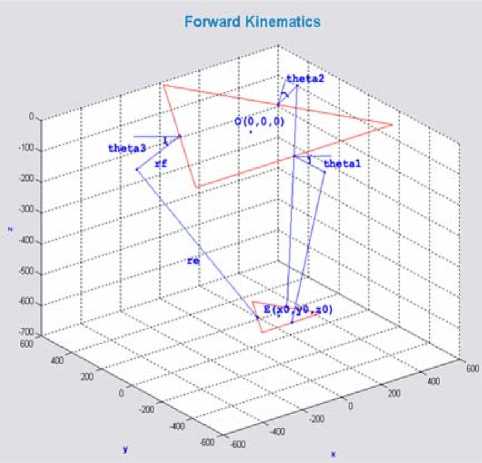
Рис. 4. Общий вид модуля решения прямой задачи в MATHLAB:

theta1, theta2, theta3 – углы между плоскостью OXY и стержнями rf; f – длина стороны верхнего треугольника; e – длина стороны нижнего треугольника; rf – длина верхнего стержня; re – длина нижнего стержня; O(0,0,0) – центр верхнего треугольника; E(x0, y0, z0) – центр нижнего треугольника

После задания всех ограничений и параметров необходимо нажать «Генерировать УП» и программа сама сгенерирует УП. Сразу после генерации появится окно, в котором будет предложено сохранить УП. Нужно выбрать необходимую директорию, присвоить имя УП и нажать «Сохранить». Расширенный формат целесообразно применять при работе с гибкими производственными системами (ГПС). Вкладка «Управление» содержит точно такой же функционал, что и в сокращенной форме. Вкладка «Настройки» показана на рис. 5. Данные, находящиеся в этой вкладке влияют на правильность работы трипода: дискретность приводов влияет на соответствие виртуального и действительного перемещения; сжатие схвата подразумевает задание наладчиком количества импульсов на сжатие или разжатие при настройке (по умолчанию в УП); максимальные и минимальные скорости влияют на скорости перемещения приводов.

При изменении каких-либо параметров необходимо сохранить их нажатием на соответствующую кнопку. В этой вкладке можно изменять параметры трипода и изменять зоны ограничения. Данные, находящиеся в этой вкладке влияют на правильность работы трипода. Пользователям рекомендуется не изменять эти настройки, за исключением поля «Радиус зоны ограничение» (именно здесь производится настройка зоны ограничения). Этот параметр можно изменять, на корректности работы трипода он не отражается. Для возврата к предыдущим значениям настройки нужно нажать «Вернуться». Вкладка «Информация» содержит отчетную информацию о выполненных командах. Вкладка «Циклограмма» показана на рис. 6. Здесь содержатся циклограммы, построенные для каждой оси трипода. Циклограмма отображает положение того или иного привода в любой момент времени, т.е. в любом кадре УП. Стенд используется для исследований точности позиционирования, возможностей гироскопических устройств, характеристик транспортных машин, станков с параллельной кинематикой, измерительных машин и роботов, погрешностей приводов при различных системах управления. Этому способствует открытость системы управления, гибкий интерфейс и приемлемые затраты на его создание.

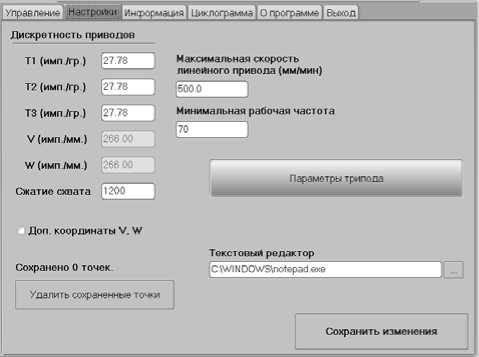
Рис. 5. Вкладка «Настройки»

Выводы: интерфейс системы управления стендом позволяет обеспечивать настройку системы в режимах ручного и автоматического управления, просмотр управляющей программы и другой информации, визуализацию положений каждого, в том числе и выходного звеньев трипода в пространстве, а также выполнять настройку осей линейных перемещения, поворотов вокруг осей (одновременно и последовательно) с изменением скоростей перемещений, дискретности, параметров зон ограничения перемещений, размеров (длины) звеньев, программировать работу схвата в исполнении «робот». Математическое обеспечение трипода позволяет решать прямую и обратную задачи, что обеспечивает возможности применения стенда для исследования, в том числе, учебных, а также для подготовки специалистов [1, 2]. При работе модуля имеется возможность ввода значений множества параметров, определяющих работу робота с параллельной кинематикой и решения прямой задачи.

Рис. 6. Вкладка «Циклограмма»