Учет геометрической нелинейности в расчетах неупругого деформирования конструкций. Декомпозиция деформации
Автор: Садаков Олег Сергеевич, Щербакова Алла Олеговна
Рубрика: Механика
Статья в выпуске: 30 (206), 2010 года.
Бесплатный доступ
На примере одноосного напряженного состояния показано разделение деформации на обратимую и необратимую составляющие. Необратимая деформация определяется пластическим удлинением, накопленным за историю деформирования, а обратимая - термоупругая - в общем случае не разделяется на упругую и тепловую. Для иллюстрации приведены два примера переменного термомеханического нагружения стержня.
Геометрическая нелинейность, упругая деформация, тепловая деформация, пластическая деформация, термомеханическое нагружение
Короткий адрес: https://sciup.org/147158648
IDR: 147158648
Текст научной статьи Учет геометрической нелинейности в расчетах неупругого деформирования конструкций. Декомпозиция деформации
Существующие методы оценки прочности конструкций в подавляющем большинстве основаны на гипотезе бесконечной малости перемещений, что существенно упрощает расчеты. Однако во многих случаях учет нелинейности может не только количественно, но и качественно изменить результат. Развитие геометрически нелинейных подходов сдерживается недостаточной пока ясностью их теоретических основ, начиная с базовых понятий о мерах напряженного и деформированного состояний [1, 2]. Определенную помощь в этом смысле может оказать анализ поведения простейших конструкций. Ниже с этой целью рассмотрен случай одноосного напряженного состояния на примере деформирования однородного неупругого стержня под действием нормальной силы и температуры.
Дисторсия
В расчетах на прочность материал конструкции моделируется в виде сплошной однородной среды. При этом делается допущение о том, что гладкие материальные волокна и пленки при деформировании остаются гладкими. Отсюда следует дифференцируемость полей смещений и(х) (х - радиус-вектор материальной точки в недеформированном состоянии). В любой точке такой среды существует градиент смещений u^=D, связывающий начальное положение элементарного материального волокна dx с его изменением du;
du = Ddx. (1)
Здесь точкой обозначено скалярное произведение ближайших к ней векторов (тензор дисторсии D представляет сумму диад). Элементарное материальное волокно dx (рис. 1) в результате деформирования и (или) поворота окрестности точки х преобразуется в волокно dr, где г - радиус-вектор материальной точки в текущий момент времени, г = х + и;
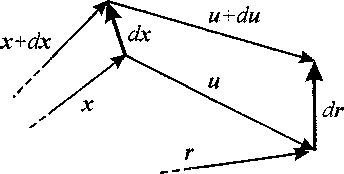
Рис. 1. Элементарное волокно до и после деформации
dr = F • dx, F = I*D, (2) I- тензор тождественного преобразования. Таким образом, бесконечное множество элементарных волокон dx в окрестности точки х смещается на величину и(х) и преобразуется в упорядоченное множество dr, определяемое двухвалентным тензором F, характеризуемым всего девятью числами (координатами). Тензор F часто неоправданно называют градиентом деформаций1. Более корректно называть его дисторсией, так как он определяет и деформацию элемента объема тела, и его поворот.
Если дисторсия вызывается разными причинами - например, тепловым воздействием (соответствующую дисторсию обозначим F^ и упругими деформациями, связанными с напряжениями
(дисторсия Fe\ - то результирующее преобразование dx^dr определяется произведением этих линейных преобразований
~ F=Fe-FT (3) (результат ряда линейных операций определяется произведением операторов). Приведенное выражение означает, что элемент объема был сначала нагрет (охлажден), а потом дополнительно деформирован приложенными напряжениями, характеризующимися тензором ст (тензор напряжений Коши в деформированной среде).
Названные дисторсии обычно бывают достаточно близки к единичному тензору I. Поэтому для удобства вводят тензоры De = Fe -1, DT = Fr- I (также называемые дисторсиями) и с некоторой погрешностью произведение (3) заменяют суммой
D=De + DT. (4) Здесь порядок воздействия (тепловое воздействие - силовое или наоборот) безразличен. Симметричные части дисторсий (4) называют деформациями е = ее + ет (та же аддитивность).
Эти довольно стандартные для прочностных расчетов выражения основываются на гипотезе о бесконечной малости составляющих дисторсии. Например, если компоненты тензора дисторсии имеют порядок одного процента, то ошибка от замены строгого выражения (3), из которого следует, что
D = фе + Г) • Фт +1) -1 - De + Dr + De • Dr суммой (4) имеет порядок 2 %.
Одноосное напряженное состояние
Переходя к более корректному (нелинейному) подходу, рассмотрим следующий простейший случай: среда изотропна, напряженное состояние одноосно. Пусть, например, это будет однородный стержень длиной /о, нагружаемый продольной силой N. Текущее значение площади поперечного сечения стержня равно S; ось стержня определяется ортом i; нормальное напряжение ст в стержне равно отношению N/S (тензор напряжений равен с^).
Деформированное состояние продольно растягиваемого стержня, очевидно, является трехосным, но нас будет интересовать только осевая составляющая деформации е = AZ/Zo (А/ - приращение длины стержня). Коэффициент длины стержня к представляет отношение Шо, где I - текущая длина стержня; отсюда к = 1 + е.
Составляющие деформации
Ограничим круг составляющих рассматриваемой деформации стержня тремя ее основными видами: тепловой, упругой и неупругой.
Неупругая деформация ер = ЫД0 (Ыр - неупругое удлинение стержня) связана со сдвигами, в результате которых происходят разрывы связей между частицами среды и устанавливаются новые - с другими соседними частицами. Это определяет необратимость неупругой деформации. Соответствующий коэффициент длины стержня равен кр = (Zo + А/рУ/о =1 + ер. (5)
Тепловая деформация, в отличие от деформации ер, обратима; она связана с изменением интенсивности теплового движения частиц среды. С ростом температуры происходит увеличение среднестатистического расстояния между частицами среды. При нагреве свободного стержня (изменение температуры обозначим 7) его длина возрастает на величину Му соответствующий коэффициент длины зависит от текущего значения Т:
кт = (/о + AZr)/Z0 = 1+ ет, Ет -ДТ). (6) Тепловая деформация свободного стержня/(7) = AZ?/Zo представляет механическую характеристику конкретного материала. При возврате к начальной температуре она становится равной нулю.
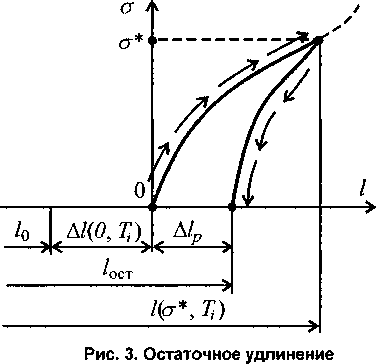
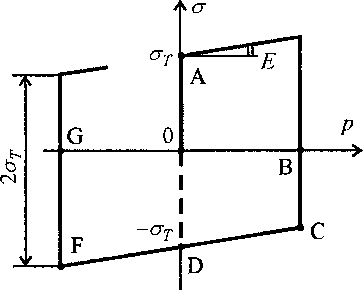
При упругом растяжении свободного стержня он вытягивается на величину AZe=g( У пру гопластическое деформирование Названные три типа деформации практически не встречаются по отдельности, но вопрос об их вкладе в общую деформацию г (или к = £ + 1) оказывается нетривиальным. Упругопластическое деформирование вполне типично: необратимые сдвиги, приводящие к пластическому удлинению стержня, вызываются напряжениями, то есть сопровождаются упругими деформациями. Необратимость пластической деформации и обратимость упругой позволяют в любой стадии упругопластического деформирования мысленно произвести разгрузку. Упругие деформации при этом исчезают, а пластическая вытяжка стержня остается. Логично считать поэтому, что пластическая деформация ер в любой момент истории нагружения определяется необратимым удлинением Мр, отнесенным к начальной длине 4; kp = 1 + sp - пластический коэффициент длины; выражение (5) относится не только к остаточному, но и к нагруженному состоянию. Возвращаясь постепенно к состоянию до начала разгрузки (восстанавливая напряжение, гипотетически положительное), заметим, что стержень длиной /0 + Мр все сильнее упруго вытягивается под действием возрастающего напряжения. При этом, очевидно, чем больше предварительная пластическая вытяжка А/Р,тем сильнее изменится длина стержня при приложении нагрузки (мы здесь полагаем, что пластическое удлинение не влияет на упругие свойства стержня, определяемые функцией g(o) (7)). Отсюда следует, в частности, что упругое удлинение пластически вытянутого стержня определяется выражением Ме№ = g Соответственно, коэффициент длины оказывается равным к кер (7о~ЪА/р~ь ^Iq^Y^Hq кекр, I А^/о- (9) Здесь ке = 1 + g(o) - зависит только от о; как и при упругой работе. Термоупругая деформация Тепловая деформация (6), как и упругая (7), обратима. Если функция g(cr) не меняется при нагреве, а функция ДТ) не зависит от нагрузки, то при упругом деформировании нагретого стержня происходит упругая вытяжка стержня длиной кт10. Результирующий коэффициент длины к = Шо = кект = (l+g^XH/T)) = 1 + g(o) +/7) + g(<7)/T). (10) То же выражение справедливо и при нагреве растянутого стержня. Однако реальная ситуация более сложна: с изменением температуры свойства упругости, очевидно, изменяются. Не исключено и влияние напряжения на коэффициент теплового расширения. Поэтому выражение (10) следует заменить, введя общий коэффициент длины кеТ, характеризующий обратимую деформацию, обобщенно определяющую влияние текущих значений напряжения и температуры кеТ= 1 + ф<о, Г). (11) Обратимая деформация (будем называть ее термоупругой) представляет собой функцию двух аргументов есТ = К о; 7) = ЫетН0, где МеТ - удлинение стержня в результате воздействия температуры и напряжения. Полагаем, что разделить ее на составляющие ее и ет в общем случае не удастся. Термоупругопластическая деформация В общем случае деформация представляет сочетание термоупругой и неупругой деформаций; первая обратима, последняя нет. При наличии пластической деформации наложение термоупругой ведет к термоупругому деформированию, в котором начальная длина /0 должна быть заменена на kplo. Напомним, что коэффициент кр определяется пластическим удлинением А7Р, отнесенным к начальной длине стержня, независимо от текущей длины (возможно, заметно отличающейся от начальной), зависящей от текущих значений ст и Г. Экспериментальное определение функции ф Каждый материал характеризуется своей функцией ф^о, 7) (рис. 2); она может быть найдена из соответствующих испытаний. Рис. 2. Часть функции ^(при а> 0, Г> 0). Выделены изотермы р(<т, Г/) Проще всего найти вначале функцию ^0, 7), замеряя деформацию нагреваемого стержня. Часто она описывается квадратной параболой <0,Г) = аТ* (12) Вторым слагаемым в этом выражении часто пренебрегают. Далее необходимы, очевидно, испытания при ненулевых напряжениях, хотя это потребует более сложной экспериментальной процедуры. Пока напряжения малы, нагретые образцы при ряде значений температуры Т = Tj =const следует растягивать или сжимать, получая при этом изотермы (р,а\ Тр^Ыру, T^/Iq. Напомним, что /0 -длина образца до нагрева и до приложения нагрузки. При разгрузке длина долж- на возвращаться к размеру / = (1+^0, T^)lQ. В частности, может выполняться закон Гука: Остаточная деформация Выявляя характеристику материала (раД), необходимо делать разгрузки, чтобы удостовериться в обратимости деформации, позволяющей использовать выражение (ро*, Т,) = (/(ст*, Т^ - /(0, 7)))/Z(0, 7Д. Здесь сг* - значение напряжения в момент начала разгрузки, Ti - значение температуры в опыте. С ростом температуры и напряжения (при выходе за некоторую условную границу, показанную на рис. 2 штриховой линией) при разгрузке начнет появляться заметная остаточная деформация (рис. 3): длина образца не возвращается к значению (1+^0,7}))/(0,7)). Это означает, что в процессе нагружения и разгрузки произошло неупругое (пластическое и/или вязкое) деформирование. Если допустить, что в процессе разгрузки неупругая деформация не изменилась, то из удлинения А/(сг*,Д), отвечающего максимальному напряжению о*, следует вычесть остаточное. Полученное удлинение позволяет найти значение термоупругой деформации в зоне неупругих деформаций: <ро*,Т^ = U(d\T,) - MPW (14) Если нет уверенности в упругости разгрузки (например, если материал обладает заметной вязкостью), то необходимо выявить реологические свойства среды, вводя и проверяя соответствующие модели пластичности и ползучести. Добавим, что этот - существенно более сложный -этап исследования в любом случае необходим для проведения прочностных расчетов конструкций. Примеры расчета Для иллюстрации приведем два простых примера расчета эволюции коэффициентов длины неупругого стержня при заданной истории нагружения. Первый пример относится к гипотетическому случаю идеально пластического материала (известны модуль Юнга Е и предел текучести (Ут). Задается история изменения температуры и коэффициента длины (табл. 1). Функция (р принята в виде До, Т) = аТ + dE. В первом столбце таблицы указан номер этапа. Таблица 1 № Температура Напряжение Коэффициент длины 1 0 ат Х+афЕ 2 Т (Ту Х+от/Е+аТ 3 Т (Ту Х+офЕ+аТ+Екз 4 0 От X-VOf/E+Акз 5 0 0 Х+Ек3 На первом этапе стержень растянут до достижения напряжением значения От. Затем при постоянном напряжении производится нагрев: стержень удлиняется (или укорачивается, если Т< 0). На третьем этапе производится вытяжка на величину А£3. Величина А£3 представляет относительное пластическое удлинение р = ЫрН0. Затем следует возврат к начальной температуре и, наконец, снятие нагрузки. Рис. 4. Модель Ишлинского-Прагера В другом примере (табл. 2) рассмотрен стержень из материала с линейным упрочнением (модель Ишлин-ского-Прагера). В этом случае может быть задана история изменения напряжения (и температуры). Вид диаграммы неупругого деформирования при изотермическом нагружении, разгрузке и нагружении обратного знака показан на рис. 4. Таблица 2 № п.п. Напряжение Температура Коэффициент длины 1 0 Д VraT\ 2 От Д \+аТ^от/Е (точка А на рис. 4) 3 от+Ео Д (1+«Т^оМ<т)/ЕХ Х+Еа/Е) 4 аНЕо 0 (l+(oz+Ao)/£)(l+Ao7£) 5 0 0 Х+Ео/Е' (точка В) 6 Ео-ат 0 (Х+(ат-Ео)/Е)(Х+Ео /Е) (точка С) 7 —(Ту 0 Х-от/Е (точка D) 8 -От~Е’о 0 (ХЦ/Тт+Е'оУЕХХ-Е'о/Е) (точка F) 9 0 Д (1+а72)(1-Д'о7£) (точка G) 10 от Т2 Х+аТ2+ог/Е (точка А) Тензор дисторсии В общем случае для описания напряженно-деформированного состояния элементов конструкций используется, очевидно, тензорный аппарат. Напряжения в деформированной среде описываются тензором напряжений Коши; другие тензоры напряжений, фигурирующие в соответствующей литературе, имеют весьма туманные обоснования. Для описания деформированного состояния, обобщая предложенную в статье идеологию, можно использовать тензор дисторсии F в виде произведения трех сомножителей F = R-VeT-Vp, (15) где Vp - симметричный тензор коэффициентов длины, связанный с неупругими деформациями; произведение трех его главных значений равно единице - ввиду требования пластической несжимаемости. Тензор VeT - симметричный тензор термоупругих коэффициентов длины, однозначно зависящих от мгновенных значений тензора напряжений и температуры. Произведение симметричных тензоров не обязательно симметрично, и произведение VeT ■ Vp , если их главные оси не совпадают, представляет произведение некоторого ортогонального тензора жесткого поворота и симметричного тензора коэффициентов длины. Кроме того, в деформируемой конструкции могут возникать дополнительные повороты, связанные с движениями остальных элементов объема среды и зависящие от граничных условий. Поэтому в выражении (15) фигурирует еще один ортогональный тензор R возможного дополнительного поворота. Он находится в процессе решения краевой (и начальной) задачи о деформировании конструкции. Заключение Приведенный анализ термоупругопластического (или термовязкоупругопластического) деформирования простейшей конструкции (например, фермы) позволил обосновать структуру коэффициента длины в геометрически нелинейном подходе, а также предложить обобщение полученных результатов на произвольное напряженно-деформированное состояние. Последнее, невидимому, потребует дальнейшего более детального расчетного обоснования.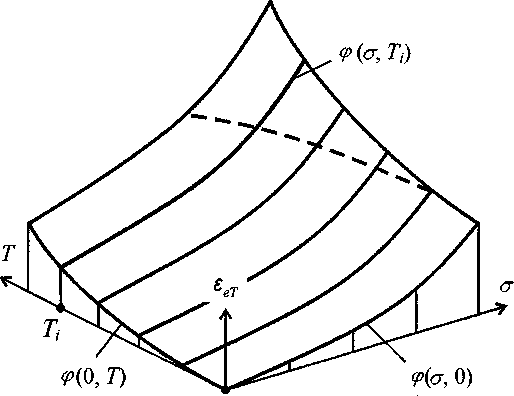
Список литературы Учет геометрической нелинейности в расчетах неупругого деформирования конструкций. Декомпозиция деформации
- Lee, E.H. Finite strain elastic-plastic theory with application to plane-wave analysis/E.H. Lee, D.T. Liu//J. Appl. Phys. -№ 38. -С. 19-27.
- Stumpf, H. Constitutive model and incremental shakedown analysis in finite elastoplasticity/H. Stumpf//Inelastic behavior of structures under variable loads. -1995. -С 293-307.
- Садаков, О.С. К расчетам напряженно-деформированного состояния конструкций в геометрически нелинейной постановке/О.С. Садаков//Труды Международной конференции «Снежинск и наука -2003. Современные проблемы атомной науки и техники». -Снежинск: СГФТА.-2003.-С. 73-74.
- Садаков, О.С. О корректности решения геометрически нелинейных задач пакетом МКЭ/О.С. Садаков, А.А. Шапиро//Вестник ЮУрГУ. Серия «Математика, физика, химия». -2003. -Вып. 4. -№ 8(24). -С. 72-77.
- Буслаева, О.С. Концепция лабораторной системы отсчета в геометрически и физически нелинейных задачах/О.С. Буслаева, О.С. Садаков, А.А. Шапиро//Математическое моделирование и краевые задачи: труды Всероссийской научной конференции 26-28 мая 2004 года. Самарский государственный технический университет. -2004. -Ч. 1. -С. 46-48.


