Учет неравномерности распределения нагрузки при расчете на контактную прочность зубчатого зацепления трансмиссии транспортной машины

Введение . В работах [1, 2] рассматривалась новая раздаточная коробка с возможностью переключения передач на ходу полноприводного автомобиля типа «Урал»: была предложена конструкция раздаточной коробки и механизма переключения передач в ней, а также рассматривались вопросы динамического нагружения трансмиссии полноприводного автомобиля, источником которого являлось кинематическое рассогласование элементов трансмиссии, возникающее при разрыве силового потока. На способ переключения передач в указанной раздаточной коробке получен патент РФ [3]. В настоящий момент ведутся работы по созданию многовальной механической коробки передач транспортных машин с аналогичным способом переключения передач, что определило необходимость более тщательного исследования нагрузочных режимов работы ее зубчатого зацепления с учетом возможных перекосов, вызванных конструктивной податливостью водила [1].

Известно, срок службы коробки передач и раздаточной коробки автомобиля-тягача лимитируется, в основном, контактной прочностью зубьев шестерен [4]. Поэтому расчетно-теоретический анализ нагруженности различных элементов трансмиссии целесообразнее начать с оценки именно зубчатой передачи. Расчеты будем проводить в следующем порядке: вначале уточним формулу для расчета усталостной прочности по контактным напряжениям зубьев ведущей шестерни входного вала; затем рассмотрим неравномерность распределения нагрузки и напряжений по длине зуба, работающего с перекосом. Для начальной простоты расчетов исследуем прямозубое эвольвентное зацепление.

В качестве исходных данных были взяты параметры зубчатого зацепления согласно табл. 1.

Таблица 1

Параметры рассчитываемого прямозубого зубчатого зацепления

Параметр	Ведущая шестерня	Ведомое колесо
Число зубьев	25	50
Модуль, мм	4
Угол зацепления, град	20
Коэффициент смещения	0,15	–0,25
Ширина, мм	40	40
Зазор боковой	0,25m	0,25m
Радиус скругления в основании зуба, мм	0,2m	0,2m
Модуль упругости, ГПа	210	210
Коэффициент Пуассона	0,3	0,3
Крутящий момент, Н·м	394

Расчет на контактную прочность. Существующая методика расчета на контактную выносливость активных поверхностей зубьев основана на формуле Герца и предусматривает определение контактных напряжений на участке профиля зуба, соответствующем полюсу зацепления. Однако, как известно, на полюсной линии выкрашивание рабочей поверхности не наступает, так как в этой точке профиля зуба происходит только качение безотносительного скольжения профилей.

Расчет рабочих поверхностей зубьев зубчатых колёс на контактную прочность основан на определении контактных напряжений в наиболее нагруженной околополюсной зоне [5]. Для этого рассмотрим, как распределяется нагрузка в зацеплении по высоте зуба (рис. 1). Энергия передаётся от шестерни к ведомому колесу по линии зацепления N ₁ N ₂ в торцовом сечении. При меньшем ведущем колесе ножка его зуба входит в контакт с головкой зуба сопряжённого колеса в точке р 2 . Точка контакта, перемещаясь по линии зацепления и по профилям зубьев, проходит зоны двупарного ( р 2 а и bр 1 ) и однопарного ab зацеплений, где приведённая удельная нагрузка q n достигает максимального значения. Приведённый радиус кривизны профилей зубьев определяют по формуле [5]:

ρ n

ρ 1 ρ 2 ρ 2 ±ρ 1 ,

где ρ 1 и ρ 2 – радиусы кривизны эвольвенты профиля зуба соответственно шестерни и колеса.

На рис. 2 показано распределение приведённой удельной нагрузки q n по рабочему участку профиля зуба. В точке а , находящейся на ножке зуба шестерни и соответствующей началу однопарного зацепления, резко возрастает q n в результате выхода из зацепления предыдущей пары зубьев.

Обозначим положение контакта зубьев на линии зацепления расстоянием f , принимая за начало отсчёта точку N 1 .

Тогда ρ 1 = f , ρ 2 = a w sin α w – f , а приведённый радиус кривизны для внешнего зацепления

ρ _n = f

f ² a_w sin α _w

где a w – рабочее межосевое расстояние; α w – рабочий угол зацепления.

Выражение (2) представляет уравнение квадратичной параболы, график которой показан на рис. 1.

Эпюра распределения приведённой удельной нагрузки q n по линии зацепления и по профилю зуба (рис. 2) показывает, что скачкообразное увеличение её до максимального значения происходит в точке а профиля зуба, в которой наиболее вероятно выкрашивание рабочей поверхности зуба шестерни, так как этот участок подвергается наибольшему числу циклов нагружения при резком возрастании q_n до максимального значения, что приведённый радиус кривизны меньше всего на участке однопарного зацепления (см. рис. 1), а поверхность ножек является «обгоняемой» и наиболее подвержена разрушению.

Расчет и конструирование

о,

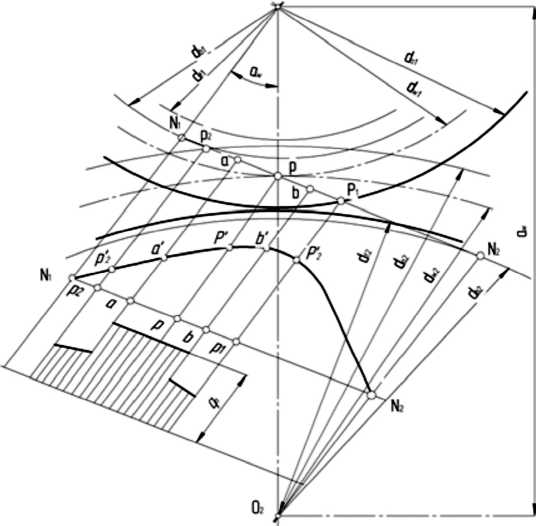
Рис. 1. Схема зацепления

Радиус кривизны профиля зуба шестерни в точке а определяется по формуле dd a1b1

I 2 I I 2 I     p b mj a .

В результате совместного решения уравнений (3) и (2) получаем формулу для определения приведённого радиуса кривизны профилей зубьев в точке а:

P n = ^mja

( mj )²

—— = _m у « w sin a w

В формулах (3) и (4) d а 1 – диаметр вершин зубьев шестерни; d b 1 – диаметр основной окруж-

ности шестерни; p b = п m cos a - шаг зацепления по основной окружности; m и a w - модуль и

угол зацепления (см. табл. 1);

j a = ^0,5 V^{( z}1 + ^{2) 2 - ( Z} 1^{COS a )}2

число зубьев шестерни; у _a = j_a

-п cos a - коэффициент числа зубьев шестерни (здесь z 1 -

2 j a

Z 1 (1 + u )sin a w

коэффициент приведённого радиуса кривизны; и – передаточное число).

Подставив значение ρ па из уравнения (4) в формулу Герца, получим конечное выражение для определения наибольшего контактного напряжения в точке а профиля зуба:

^ст На = ^Z e Z E

2 M ■ E ■ K H

\ d a b ' ^ma p Y a cos ^a V

где Z _ε и Z_E – коэффициенты, учитывающие соответственно суммарную длину контактных линий и механические свойства материалов сопряжённых зубчатых колёс; K_H – коэффициент, учитывающий

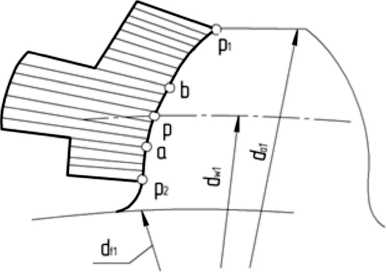
Рис. 2. Схема распределения нагрузки по рабочему участку профиля зуба

неравномерность распределения нагрузки; М – крутящий момент на шестерне; Е – модуль упругости материала зубчатого колеса [5]; b' – контактная ширина пары зацепляющихся зубчатых колёс в полюсе зацепления, m – модуль зацепления; а p – число контактирующих шестерен; d а – начальный диаметр окружности шестерни; a w - угол зацепления (см. рис. 1).

В точке b на линии зацепления (в конце фазы однопарного зацепления) в зацеплении находятся ножка зуба шестерни и головка зуба зубчатого колеса. Приведённая удельная нагрузка в этой точке профиля зуба (рис. 3) наибольшая, а приведённый радиус кривизны значительно больше, чем в точке a . Контактные напряжения в точке b меньше, чем в точке a .

В точке b приведённый радиус кривизны

Р nb = m Y b ,                                                                                       ⁽⁶⁾

где Y b = j b

(   z1 (1 + u ) sin aw ,

– коэффициент приведённого радиуса кривизны; j b – коэффи-

циент чисел зубьев колеса,

j b = 0,5

z 1 (1 + u )sin a w - дД z 1 u + 2) 2 - ( z 1 u cos a w )² + n cos a .

Подставляя выражение (2.10) в формулу Герца, получаем:

^ Hb

= Z _£ Z e

2 M ■ E ■ K_H

\j d b ma p b ' Y b cos a _w "

Таким образом, как видно из формул (5) и (7) контактные напряжения на зубе шестерни прямо пропорциональны моменту М на шестерне и коэффициенту неравномерности распределения нагрузки K_H .

Расчет распределения нагрузки и напряжений. Рассмотрим случаи и решения с привлечением ряда допущений: выступ прямоугольной формы заменяет прямые зубья цилиндрических колёс; нагрузка прилагается к вершине, причём распределена она по всей длине выступа (см. рис. 3).

При расчете распределения нагрузки и напряжений по длине зуба будем исходить из того, что в работающей зубчатой передаче вследствие упругой деформации её деталей под нагрузкой и несовершенства конструкции возникает перекос осей зубчатых колёс. При абсолютно жёстких

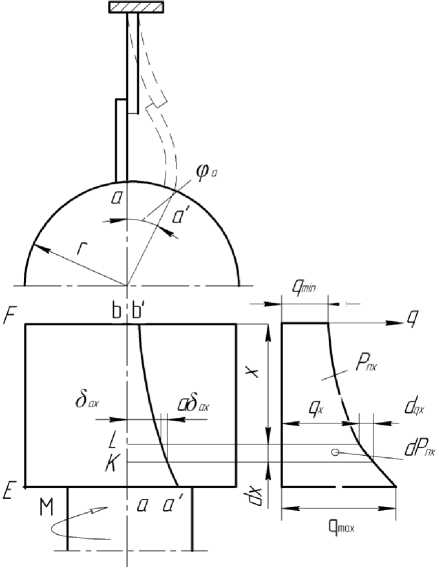
Рис. 3. Схема распределения удельных давлений по ширине зубчатого венца

зубьях перекос повлёк бы за собой их угловой контакт. В действительности контакт сохраняется по всей длине зубчатых колёс или на части её, поэтому давление вдоль контактных линий распределяется неравномерно.

При рассмотрении работы зубьев есть предположение [6], что нагрузка распределяется по законам трапеции или треугольника. Считают, что такой характер нагрузки в значительной степени зависит от того, как изменяется упругая податливость зубьев по длине.

Существует мнение, что зуб у края нагружен меньше, чем на удалении от него, в том числе и при перекосах [6], хотя краевые поломки встречаются часто [7, 8]. Отмечается повышенная податливость крайней части зуба, что требует подтверждения, поскольку прогиб в какой-либо точке определяется не только нагрузкой в этой точке, но и нагрузкой в других точках контактной линии. Механизм краевого эффекта связан с коэффициентом Пуассона. При µ = 0 равномерный прогиб прямого зуба сопровождался бы равномерным распределением нагрузки.

Расчет и конструирование

Контактные деформации рассматриваем в предположении линейной связи между удельной нагрузкой q и перемещением у 0 = Cq . Для напряжённого состояния в выступе наиболее важно следующее допущение: принимаем равными нулю нормальные напряжения, действующие вдоль зуба, что необходимо для получения наиболее простых расчётных формул. В действительности такие напряжения имеют место. В частности, при равномерном изгибе зуба они равны: σ y = µσ x (σ x – нормальные изгибающие напряжения). В дальнейшем распределение напряжений по высоте и толщине выступа принимаем по простейшим линейным и квадратичным зависимостям.

Углы поворота сечений, перпендикулярных оси, ввиду деформаций кручения тела центрального колеса не одинаковы. Максимальный угол φа соответствует торцу Е со стороны подвода момента М, а минимальный угол φb – у торца F (см. рис. 3). В соответствии с этим изменяются и перемещения δ0 точек образующей ab, начиная от δ0a = аа' = r0φа и кончая δ0b = bb' = r0φb. В этом случае q = Cδ0, (8) где q – удельная контактная нагрузка, Н/м2, приходящаяся на единицу ширины зубчатого венца; С – коэффициент удельной жёсткости зубьев, Н/м2 [7]. Таким образом, деформация кручения тела зубчатого колеса вызывает неравномерность распределения удельных давлений q по ширине зубчатого венца.

Для сечения L , находящегося на расстоянии х от торца F, имеем qx = Сδ0x= Сr0φx , (9) где φδ – угол поворота сечения L после приложения нагрузки; r0 – радиус окружности впадин шестерни.

Далее имеем

Pard nx p x

GJ k ^,

Md

d 6Y = — x GJk где G – модуль сдвига, Н/м2 [7, 8]; Jк – момент инерции шестерни; Jк = 0,1d4(1–β4), где β – отношение диаметра отверстия шестерне, к диаметру, принимаемому за расчетный при определении момента инерции.

Из формул (9) и (10) получим

Ca_pr ₀ ²

dq = —~— Pxdx, x nx x

GJk

или

dqx dx

^{H 1} nx ,

где

Ca_pr ₀ ² GJ k

Далее имеем dP_nx=q_xdx , dq_x = d ² P nx d      d ^{2 .}

xx

На основании равенств (12) и (15) получим уравнение ² dP_{nx   2}

H ^Pnx = 0 .

dx ²

Для нашего случая выражение (16) примет вид

² nx 2

, 2 ^H P nx ^{a ,} dx ²

где α – некоторая постоянная величина. Решение уравнения (17) имеет вид

P nx

a

h ²

a введём обозначение — = k , тогда получим ц

P_nx = С 1 e + С ₂ e ^{-ц х} - k .

При х = 0 и х = b имеем соответственно Рnx = 0 и Рnx = Рп, где Рп – полное нормальное усилие в зацеплении, тогда

C 1 = –C 2 + k.

Вычтя равенство (19) из равенства (18), получаем

Ci =

nx

P_n + k - ke ^{-ц b}

2sh( ц b )   ;

( P_n + k )sh( p x ) + k sh( ц b - p x ) k

"              sh( ц b )                  ,

на основании равенства (14) имеем qx

dPnx _   ц

dx

_ Qx _ qcp

sh ( ц b ) ц b

[ ( P n + k )ch ^ x - к ch( ц b - ц л ) ] ;

P n ^sh( Ц ^b )

[ ( P n + k )ch( ^ x ) - k ch( ц b - ^ x ) ] .

С учетом угла перекоса зубьев γ в плоскости зацепления, на основании формул (20) и (21) получим dQx = C(rodфX - Ydx) = (ц2Pnx - Cy) dx .

Из формул (15) и (17) имеем

d ² P nx dx ²

ц ² P nx =- c y .

a

Сравнивая равенства (24) и (17) при k = — для рассматриваемого случая, имеем ц

k=-CY .

ц

На основании равенства (23) получим

= Qx =   цb qcp   Pnsh(цbb)

C ^ I ch( ^ x ) - C ^еН( ц b -ц х ) , ц ² J ц ²

тогда при х = 0 и х = b имеем систему из двух уравнений

K

= Q x = 0 = H b

H = qcp

n

v _ qx = b _ ^{ц b} K H =----= ,>

q cp    P n

P n

C y ц ²

sh( ц b )

P n

Cl

Ц 2

Cy ц2 th(цb)

CY

Ц 2

th( ц b )   sh( ц b )

;

.

Величина коэффициента K t , которым учитывается неравномерность распределения удельных контактных нагрузок по ширине зубчатого венца, равна большему значению из двух отношений (27) и (28).

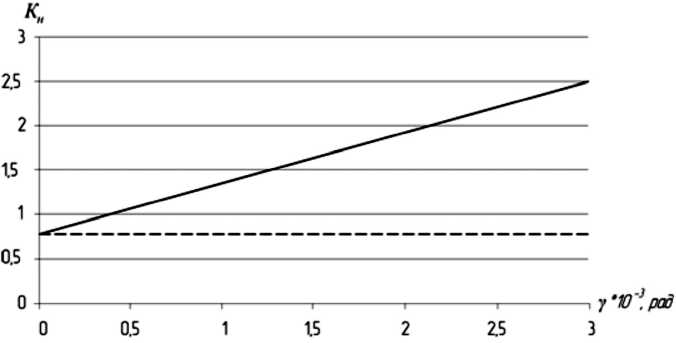
Анализируя выражения (27) и (28), получаем зависимости коэффициента неравномерности распределения нагрузки K Н от усилия на зубе Р Н (рис. 4) и угла перекоса в зацеплении γ (рис. 5).

Как видно из рис. 4 и 5, зависимость коэффициента K_H , от усилия на зубе носит обратно пропорциональный характер, т. е. при увеличении нагрузки на зубе неравномерность уменьшается, а зависимость K_H от угла перекоса γ носит прямо пропорциональный характер.

Расчет и конструирование

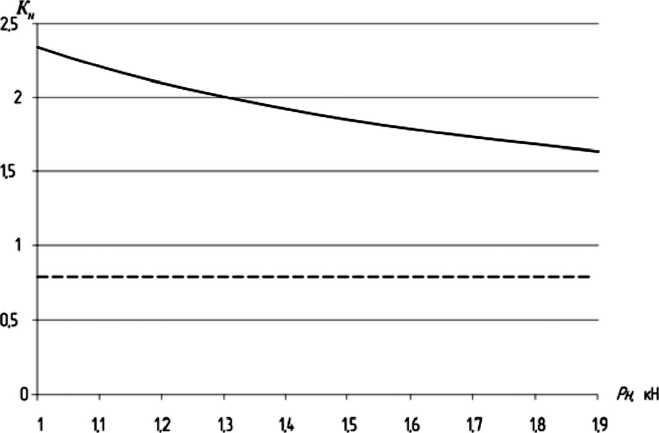
---------с перекосом------без перекоса

Рис. 4. Зависимость коэффициента неравномерности распределения нагрузки от усилия на зубе

-------с перекосом----без перекоса

Рис. 5. Зависимость коэффициента неравномерности распределения нагрузки от угла перекоса

Полученные расчетным путем значения K_H были сопоставлены с экспериментальными данными ряда исследователей. Так, из работ [5, 7, 8] известно, что коэффициент неравномерности должен быть: K H <  2, в противном же случае при K H >  2 нагрузка будет распределяться лишь по части зубчатого венца. В нашем случае, как видно из табл. 2, имеет место именно такое условие ( K H >  2).

Таблица 2 Исходные данные и результаты расчета коэффициента K Н

№ п/п	Наименование показателей	Усл. обознач.	Ед. изм.	Вариант
				I	II	III
1	Полное нормальное усилие в зацеплении	Р Н	кН	12,74	10,43	10,10
2	Коэффициент Пуассона	µ	–	0,25
3	Рабочая ширина зуба	b	м	0,05
4	Коэффициент удельной жёсткости зубьев	С	Н/м2	1,5 - 1010
5	Результирующий угол перекоса сопряжённых колёс	γ	рад	0,002	0,002	0,002
6	Коэффициент неравномерности	K H	–	2,37	2,63	2,69

Вывод . Для исследования характера распределения нагрузки и напряжения по длине зубьев, работающих с перекосом, были адаптированы и применены известные зависимости [5] по расчету распределения нагрузки по длине прямых зубьев, работающих без перекоса, а также был применен вариационный энергетический метод применительно к консольной пластине, заменяющей зуб. Это позволило, в отличие от принятых методик [4, 6, 8], не разбивать на две самостоятельные единую задачу расчёта нагрузок и изгибающих моментов в заделке. Сравнение полученных расчетных значений с экспериментальными данными других авторов показало высокую сходимость результатов.