Учет влияния параметров двухцепных ЛЭП при симметричных коротких замыканиях при коррекции установок релейной защиты
Автор: Назаров А.В.
Журнал: Мировая наука @science-j
Рубрика: Естественные и технические науки
Статья в выпуске: 7 (7), 2017 года.
Бесплатный доступ
При расчете управляющего воздействия противоаварийной автоматики, при выборе уставок релейной защиты, а также при оперативном ведении и корректировке текущих режимов энергосистем необходимо учитывать влияние параллельных цепей двухцепных ЛЭП. Cтатья посвящена анализу учёта взаимовлияния двухцепных воздушных линий при расчёте токов короткого замыкания.
Двухцепная лэп, взаимная индукция, метод фазных координат
Короткий адрес: https://sciup.org/140262891
IDR: 140262891
Текст научной статьи Учет влияния параметров двухцепных ЛЭП при симметричных коротких замыканиях при коррекции установок релейной защиты
В практике сегодняшних дней для обеспечения надежности электроснабжения питание потребителей достаточно часто резервируется по двум идентичным линиям, которые из соображения экономической целесообразности выполняются на одной несущей опоре. В нормальном режиме работы линий переток мощности распределяется по обеим цепям равномерно и может считаться приблизительно одинаковым. Такие двухцепные линии в основном встречаются в сетях 35, 110 и 220кВ, значительно реже они используются при напряжении 330кВ.
При уменьшенных расстояниях между осями параллельных ВЛ становится заметным влияние цепей друг на друга через взаимную индуктивность и емкость. Это влияние приходится учитывать при выборе уставок релейной защиты (РЗ), при расчете управляющего воздействия противоаварийной автоматики (ПА), а также при оперативном ведении, управлении и коррекции текущих режимов энергосистем.
Традиционные методы расчета симметричных КЗ базируются на симметричности элементов сети. Для учета несимметрии, взаимоиндукции разных фаз друг на друга, расположения проводов ВЛ и других особенностей применяют метод фазных координат, который в практической реализации сталкивается с рядом трудностей, ограничивающих его применение в алгоритмах расчета.
Данная статья посвящена анализу методов, учитывающих свойства двухцепных ЛЭП на точность расчёта симметричного режима трехфазного КЗ на одной из линий двухцепной ЛЭП с целью корректировки уставок РЗ и ПА.
В качестве тестируемой модели был рассмотрен участок сети между понижающими станциями (ПС) 500кВ «Киндери» и ПС 220кВ «Центральная», соединенные двухцепной ВЛ 220кВ со следующими параметрами: линия двухцепная на одностоечных опорах типа П220-2; длина линии: L=25,843км; марка проводов: АС-300/39; вид опор: анкерные, анкерно-угловые, промежуточные; расщепление фаз: нет; транспозиция проводов: нет; наличие грозозащитных троса: 2 троса; частота заземления грозозащитного троса: по концам ЛЭП – глухое заземление, по линии – через разрядные рога.
В качестве тестируемой модели был рассмотрен участок сети между понижающими станциями (ПС) 500кВ «Киндери» и ПС 220кВ «Центральная», соединенные двухцепной ВЛ 220кВ со следующими параметрами: линия двухцепная на одностоечных опорах типа П220-2 (рис.1.); длина линии: L=25,843км; марка проводов: АС-300/39; вид опор: анкерные, анкерно-угловые, промежуточные; расщепление фаз: нет; транспозиция проводов: нет; наличие грозозащитных троса: 2 троса; частота заземления грозозащитного троса: по концам ЛЭП – глухое заземление, по линии – через разрядные рога.
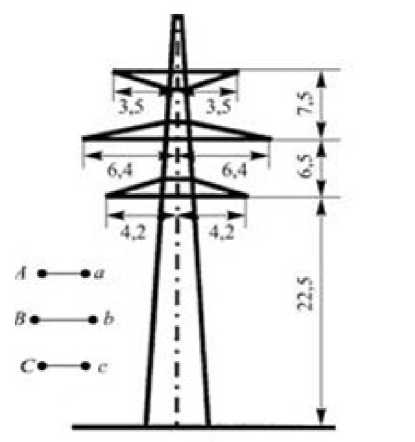
Рис. 1. Двухцепная опора П220-2 (расстояния указаны в метрах)
В качестве расчетного эксперимента выполнялся расчет периодической составляющей начального тока симметричного трехфазного КЗ на шинах приемной ПС «Центральная» (рис.2). ПС «Киндери» считаем источником бесконечной мощности с собственным сопротивлением равным нулю.
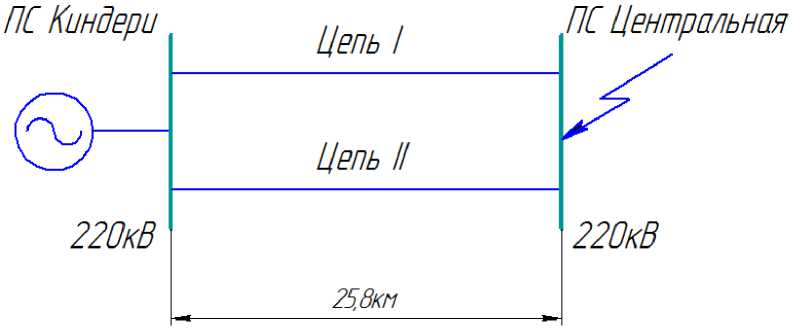
Рис.2. Исследуемая сеть ВЛ 220кВ ПС «Киндери-Центральная»
При моделировании сети производились вычисления для расчетных моделей отображающих в формате обобщенной многопроводной схемы замещения ВЛ с сосредоточенными параметрами с использованием матрица расстояний между проводами различных фаз (табл.1)
Табл.1. Матрица расстояний между проводами различных фаз.
|
d(м) |
A |
B |
C |
a |
b |
c |
|
A |
- |
d AB |
d AC |
d Aa |
d Ab |
d Ac |
|
B |
d AB |
- |
d AC |
d Aa |
d Ab |
d Ac |
|
C |
d AC |
d Aa |
- |
d Aa |
d Ab |
d Ac |
|
a |
d AC |
d Aa |
d Ab |
- |
d Ab |
d Ac |
|
b |
d AB |
d AC |
d Aa |
d Ab |
- |
d Ac |
|
c |
d AB |
d AC |
d Aa |
d Ab |
d Ac |
- |
Расчет проводился по трем вариантам. По первому варианту был проведен расчет сопротивлений и периодической составляющей начального тока симметричного трехфазного КЗ на шинах приемной ПС по однолинейной схеме ЛЭП без учета взаимоиндукции. Сопротивление цепи было рассчитано по известной формуле:
Z = (r пр + j0,145-lg^)
• L,
1 ЭК где Rпр – удельное активное сопротивление провода; rэк – эквивалентный радиус провода; Dср – среднее геометрическое расстояние между фазами одной цепи.
По второму варианту расчет сопротивлений и периодической составляющей тока трехфазного КЗ был проведен по однолинейной схеме
ЛЭП с учетом взаимоиндукции. Сопротивление цепи было рассчитано по известной формуле:
Z^" = (rпр + j0,145-lg^VL,
‘ эк '
где D I-II – среднее геометрическое расстояние между цепями I и II.
Для третьего варианта составлена матрица собственных и взаимных фазных сопротивлений (табл.2).
Табл. 2. Матрица собственных и взаимных фазных сопротивлений.
|
I цепь |
II цепь |
||||||
|
7 Z ij |
A |
B |
C |
a |
b |
c |
|
|
I |
A |
Z AA |
Z AB |
Z AC |
Z Aa |
Z Ab |
Z Ac |
|
B |
Z BA |
Z BB |
Z BC |
Z Ba |
Z Bb |
Z Bc |
|
|
C |
Z CA |
Z CB |
Z CC |
Z Ca |
Z Cb |
Z Cc |
|
|
II |
a |
Z aA |
Z aB |
Z aC |
aa |
Z ab |
Z ac |
|
b |
Z bA |
Z bB |
Z bC |
Z ba |
Z bb |
Z bc |
|
|
c |
Z cA |
Z cB |
Z cC |
Z ca |
Z cb |
Z cc |
|
По главной диагонали матрицы располагаются собственные сопротивления фаз:
Z(собств) = (Rпр + R3 +7'0,145 ■ lg^)-L , 1 эк где R3=0,05 Ом/км – удельное сопротивление земли; D3 – глубина залегания фиктивного обратного провода при f=50Гц.
Недиагональные элементы составляют взаимные сопротивления между фазами:
Z ( «заим ) = №+7'0,145-1а ^ )-L .
Имеем 6 исходных уравнений падения напряжения на фазах линии для трехфазного металлического КЗ:
^UA=lA-ZAA+IB-ZAB+lc-ZAC+la-ZAa+Ib-ZAb+lc-ZAc bUB=IA^ZBA+IB^ZBB+I c ^ZB c +I a ZBa+Ib^ZBb+I c ^ZB c ^U c =lAZ cA +l B^CB +l c Z cc +l a Z ca +l b Z cb +l^Z cc ^Ua=IA•Za A +Iв•Z aв +Ic•Za c +I a Zaa+Ib-Za b +I c Za c ^U b =lAZ bA +lB-Z bB +l c Z bc +l a ^ыЛМьИ-^Ьс
MJc=IA-ZcA+lB-ZcB+lG-ZcC+la-Zca+Ib-Zcb+Ic-Zcc
Принимаем допущение что параметры линий цепи I и II равны, так же соответственно равны напряжения на шинах ПС Киндери одноименных фаз:
MJA=MJa=EA Ы)в=Ы1ь=Ев ^Jc=^Jc=Ec
Тогда токи одноименных фаз также будут соответственно равны: i A =ia; 1 в =1ь; I c =I c ;
А исходная система уравнений упроститься и примет вид: ^J A =I A ^(Z AA +Z Aa) +I B '(Z ab + аь ) +I C*(Z . ac +Z ac ) ^J b =I a (Z ba +Z bu) +I b - (Z BB +Z Bb) +I c (Z bc +Z bc^ ^J c =I a (Z cA +Z ca ) + I b - (Z cB +Z cb) +I c ^(Z cc +Z cc )
Матрица действующих значений токов КЗ:
|I 1= |Z|-1 -| J| где U – матрица со значением ЭДС источника питания в каждой фазе; Z – матрица сопротивлений, учитывающая взаимовлияние фаз от расположения цепей на опорах и грозозащитного троса.
Результаты расчётов запишем в виде таблицы 3,4, 5 и 6.
Для провода марки АС-300/39: R o =0,0958 (Ом/км) – удельное погонное активное сопротивление провода; rпр=12 (мм) – радиус провода; rэк =11,4(мм) – эквивалентный радиус; Rпр=2,47 (Ом) – полное активное сопротивление провода фазы.
Табл. 3. Расстояние между проводами различных фаз
|
d(M) |
A |
B |
C |
a |
b |
c |
|
A |
- |
8,04 |
14,02 |
7,00 |
12,42 |
15,98 |
|
B |
8,04 |
- |
6,86 |
12,42 |
12,80 |
12,43 |
|
C |
14,02 |
6,86 |
- |
15,98 |
12,43 |
8,40 |
|
a |
7,00 |
12,42 |
15,98 |
- |
8,04 |
14,02 |
|
b |
12,42 |
12,80 |
12,43 |
8,04 |
- |
6,86 |
|
c |
15,98 |
12,43 |
8,40 |
14,02 |
6,86 |
- |
Табл. 4. Собственные и взаимные фазные удельные индуктивные сопротивления
|
Х(Ом/км) |
A |
B |
C |
a |
b |
c |
|
A |
0,7167 |
0,3037 |
0,2687 |
0,3125 |
0,2764 |
0,2605 |
|
B |
0,3037 |
0,7167 |
0,3137 |
0,2764 |
0,2745 |
0,2763 |
|
C |
0,2687 |
0,3137 |
0,7167 |
0,2605 |
0,2763 |
0,3010 |
|
a |
0,3125 |
0,2764 |
0,2605 |
0,7167 |
0,3037 |
0,2687 |
|
b |
0,2764 |
0,2745 |
0,2763 |
0,3037 |
0,7167 |
0,3137 |
|
c |
0,2605 |
0,2763 |
0,3010 |
0,2687 |
0,3137 |
0,7167 |
Табл. 5. Собственные и взаимные фазные удельные активные сопротивления
|
R(Om/km) |
A |
B |
C |
a |
b |
c |
|
A |
0,1458 |
0,05 |
0,05 |
0,05 |
0,05 |
0,05 |
|
B |
0,05 |
0,1458 |
0,05 |
0,05 |
0,05 |
0,05 |
|
C |
0,05 |
0,05 |
0,1458 |
0,05 |
0,05 |
0,05 |
|
a |
0,05 |
0,05 |
0,05 |
0,1458 |
0,05 |
0,05 |
|
b |
0,05 |
0,05 |
0,05 |
0,05 |
0,1458 |
0,05 |
|
c |
0,05 |
0,05 |
0,05 |
0,05 |
0,05 |
0,1458 |
Табл. 6. Периодические составляющие начального тока симметричного трехфазного КЗ и их отклонения от тока I A(3)
|
Метод расчета |
Фазные токи |
I(3) ф.по (кА) |
∆ I (кА) |
δ I (%) |
|
1 |
I A = I B = I C |
11,4 |
1,39 |
13,89 |
|
2 |
I A = I B = I C |
11,15 |
1,14 |
11,39 |
|
I A = |
10,01 |
0 |
0 |
|
|
3 |
I B = |
11,94 |
1,93 |
19,28 |
|
I C = |
10,85 |
0,84 |
8,39 |
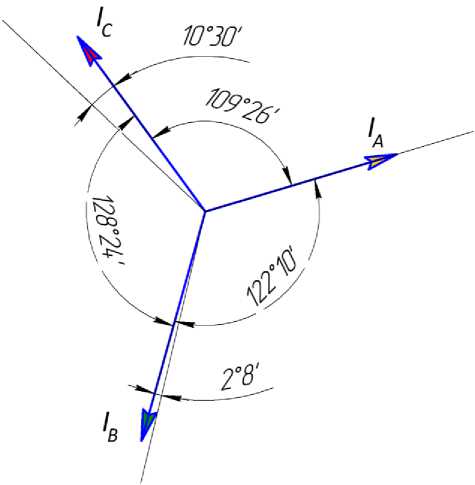
Рис.3. Вектора периодической составляющей тока трехфазного КЗ.
Если принять за эталон наименьшее значение тока в фазе А, рассчитанного по методу фазных координат, то относительные и абсолютные отклонения можно изобразить в виде гистограммы (рис.4).
IA(3) 100 %
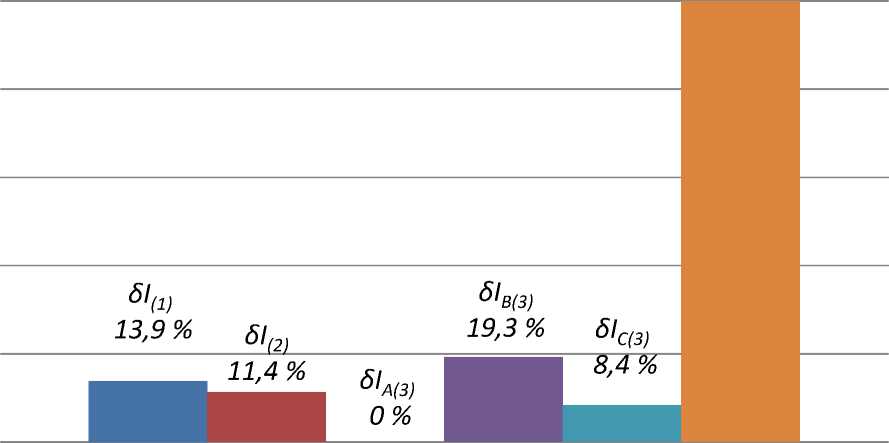
Рис.4. Относительное отклонение расчетных токов от тока IA (3) (%)
Полученные результаты позволяют сделать вывод о том, что неучёт свойств двухцепных ЛЭП и взаимного влияния их друг на друга приводит к заметным погрешностям в расчетах симметричного короткого замыкания.
При расчёте токов КЗ для целей релейной защиты нельзя пренебрегать влиянием свойств параллельных линий. От учёта внутренних свойств при расчёте уставок зависит чувствительность работы РЗ и частота их ложных срабатываний. Приоритетными задачами являются сокращения количества ложных срабатываний вплоть до их исключения.
Список литературы Учет влияния параметров двухцепных ЛЭП при симметричных коротких замыканиях при коррекции установок релейной защиты
- Берман А. П. Расчет несимметричных режимов электрических систем с использованием фазных координат. - Электричество, 1985, № 2.Взаимовлияние двухцепных воздушных линий и их воздействие на режим электрических систем / М.Ш. Мисриханов, В.А. Попов, Н.Н. Якимчук, Р.В. Медов // Электрические станции. - 2001 - №2.
- Гусейнов А. М. Расчет в фазных координатах несимметричных установившихся режимов в сложных системах. - Электричество, 1989, № 3
- Закорюкин В.П., Крюков А.В. Сложнонесимметричные режимы электрических систем. - Иркутск: Изд-во ИГУ. - 2005. - 273с.
- Руководящие указания по релейной защите / Вып. 11. Расчеты токов короткого замыкания для релейной защиты и системной автоматики в сетях 110-750 кВ. - М.: Энергия, 1979, №11
- Ульянов С.А. Электромагнитные переходные процессы в электрических системах. - М.; Л.: Энергия,1970.


