Удар по спортивному мячу

Во многих игровых видах спорта достижение результата зависит от формы траектории движения центра масс спортивного мяча. При движении мяча в воздухе на него действуют аэродинамические силы, которые существенно зависят от скорости движения центра масс мяча и его угловой скорости. Для решения дифференциальных уравнений движения центра масс мяча необходимо знание начальных условий движения. Начальную скорость движения центра масс и угловую скорость вращения мяч получает после удара по нему или после отскока мяча от игровой площадки. Как показывает анализ материалов конференций по биомеханике спорта [1] - [5], отмеченным вопросам в спортивной науке уделяется большое внимание. Работы посвящены, в основном, исследованию упругих свойств мяча и ударяющего тела для конкретных видов спорта: теннис, гольф, бейсбол. Некоторые задачи математического моделирования движения мяча в сопротивляющейся среде и частные случаи удара по мячу рассмотрены в работах [6] - [10].

В настоящей работе при рассмотрении удара по мячу используются основные допущения классической теории идеализированного удара [11]: время ударного взаимодействия считается пренебрежимо малым, в фазе удара учитываются только ударные силы и считается, что перемещением мяча за время удара можно пренебречь. Применены теоремы об изменении количества движения мяча при ударе mu -mv = ^8k                         (1)

k = 1

и кинетического момента мяча относительно осей прямоугольной декартовой системы координат Cx 1 x ₂ x ₃, связанной с центром масс мяча и движущейся поступательно (система Кёнига):

n

J ( ω x_i -ω 0 x_i ) = ∑ m Cx_i ( S k^e ), i = 1,2,3.                       (2)

k = 1

Здесь m - масса мяча, v - скорость его центра масс в начале удара, и - в конце удара, S_k ^e - импульс внешней ударной силы, J – момент инерции сферы относительно центральной оси, 6 0 - угловая скорость мяча в начале удара, 6 - в конце удара.

Коэффициент восстановления при ударе равен отношению проекций относительных скоростей центра масс мяча в конце удара и в начале удара на общую нормаль к поверхностям соприкасающихся тел:

k = u_n - w_n / v_n - w_n ,                              (3)

где w - скорость тела, ударяющего по мячу, постоянная в фазе удара в предположении, что масса мяча много меньше массы ударяющего тела.

Рассмотрены случаи непроскальзывания и проскальзывания мяча по ударяющей поверхности. Коэффициент восстановления k и коэффициент трения f находятся экспериментально.

• 2.    Удар по неподвижному мячу

• 2.1.    Случай непроскальзывания. На рис. 1 изображено сечение мяча ударной плоскостью. Считаются заданными положение точки удара M , определяемое углом ϕ , модуль w вектора скорости удара и угол γ , составляемый этим вектором с нормалью к поверхности мяча. Надо найти скорость движения центра масс мяча и и его угловую скорость 6 в конце удара.

Рассматривается нецентральный удар ракеткой или каким либо другим телом по мячу сферической формы, покоящемуся до удара в инерциальной системе отсчета 0 xyz (рис. 1). Удар производится по точке M мяча со скоростью w , составляющей угол у с нормалью к поверхности Mn . Плоскость, в которой лежат вектор w и центр масс мяча С , будет называться ударной плоскостью (плоскость M τ n на рис. 1). Предполагается, что вектор ударного импульса S также лежит в этой плоскости. Для мяча сферической формы это предположение достаточно очевидно и оно подтверждается опытом. Сначала рассмотрена подача мяча накатом (верхнее вращение мяча). Отдельно исследуются случаи непроскальзывания и проскальзывания мяча по поверхности ударяющего тела.

Поскольку до удара мяч покоился, то теоремы об изменении количества движения мяча в проекциях на естественные оси и его кинетического момента относительно центра масс С примут вид:

mu _τ = S _τ , mu_n = S_n , J ω= S _τ r , (4)

где r - радиус мяча, J = 2mr2 /3 - его осевой момент инерции. Коэффициент восстановления u - wcos γ k= n

w cos γ

В случае непроскальзывания мяча тангенциальная составляющая скорости точки М мяча в конце удара равна тангенциальной составляющей скорости ударяющего тела, и теорема сложения скоростей дает соотношение:

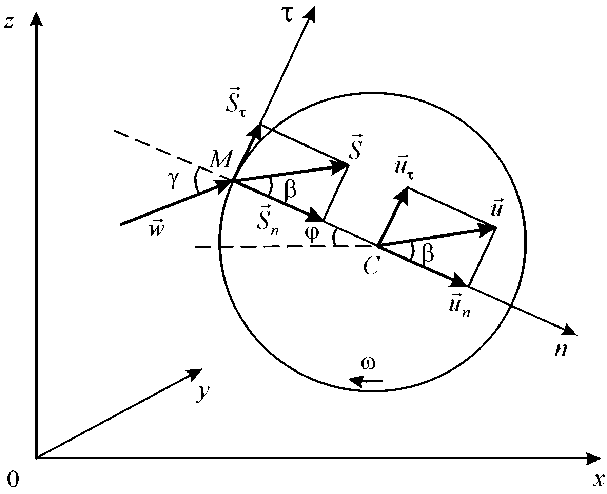
Рис. 1. Удар по неподвижному мячу

w sin y = и т+го r .                                 (6)

Из уравнений (4) – (6) находятся искомые величины:

и = — w sin y , и = (1 + к ) w cos y , ro = — w sin y .                (7) 1    5               "                             5 r

Угол в вектора и с нормалью находится из формулы

	2 tg в= ..      tg Y,                                      (8) 5(1 + к )
а его модуль	(f 2     ^ 2                У/' и = 1 —sin y| + (( 1 + к ) cos y ) 2     w                      (9) V( 5      )                 )
Полученные непроскальзывания:	результаты справедливы лишь при выполнении условия S I= tg в< f • Sn

С учетом (8) это условие записывается в виде:

5(1 + к ) - tg Y< 2 f •                              (10)

Например, при к = 0,6, f = 0,75 (ракетка для настольного тенниса с мягким покрытием) критическое значение угла Y * = 72 ° . При углах у > у * следует учитывать проскальзывание мяча по ракетке. Формула (8) хорошо согласуется с опытными данными. Удар выполнялся при у = 45 ° < у * . Опытные значения угла в получались близкими к расчетному значению в = 14 ° •

В рассмотренном случае ударная плоскость вертикальна и мячу придается вращение по часовой стрелке (накат). При подрезке (обратное вращение мяча) точка удара М лежит ниже центра масс C , углы γ и β откладываются в другую сторону от нормали Mn . В этом случае сохраняются все расчетные формулы, полученные для наката. Эти формулы справедливы и при произвольной ориентации ударной плоскости в декартовой системе координат 0 xyz . Исследователю надо будет перейти от естественной к декартовой системе координат. Например, в рассмотренном случае векторы w и й с осью 0 x составляют углы y - Ф и в - Ф , соответственно (ударная плоскость лежит в координатной плоскости 0 xz ).

• 2.2.    Случай проскальзывания. Пусть угол удара γ > γ_∗ . Тогда мяч будет проскальзывать по поверхности ударяющего тела, и кинематическое условие (6) необходимо заменить формулой для коэффициента трения скольжения:

f =Sτ/Sn.(11)

Уравнения (4), (5), (11) имеют решение:

3u un =(1+k)wcosγ, uτ = fun, ω= f n .(12)

2 r

Интересно, что вектор й составляет с нормалью Mn угол в , не зависящий от угла удара γ и равный углу трения:

tg β = f .(13)

Как показывает анализ результатов, полученных в пунктах 2.1 и 2.2, угловая скорость ω при изменении угла γ от 0 ° до 90 ° сначала растет от 0 до своего наибольшего значения при γ = γ_∗ , а затем убывает до 0 при γ = 90 ° . Эти выводы имеют не только теоретическое, но и практическое значение.

• 3.    Удар по движущемуся мячу

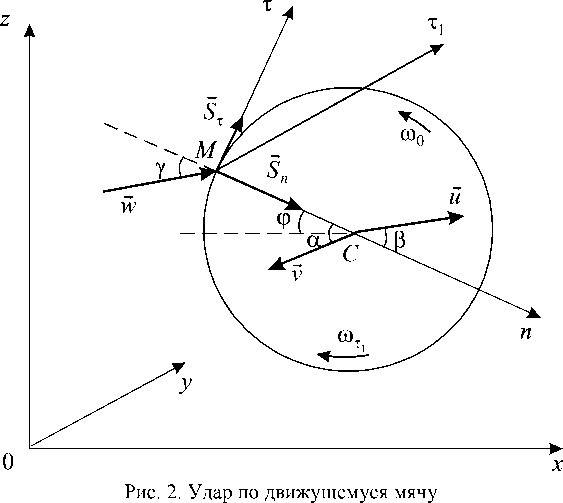
• 3.1.    Случай плоскопараллельного движения. Пусть до удара все точки мяча движутся в плоскостях, параллельных координатной плоскости 0 xz . В момент начала удара скорость центра масс мяча равна v и его угловая скорость равна го ₀. На рис. 2 показано сечение мяча ударной плоскостью, параллельной плоскости 0 xz . Введем естественную систему координат Mn τ ₁ τ . Ось τ ₁ параллельна оси 0 y , оси Mn , M τ лежат в ударной плоскости . Теоремы теории удара имеют вид:

Ранее рассмотрен удар по неподвижному мячу, что характерно для подачи мяча во многих видах спорта. При приеме мяча надо учитывать его движение до удара. Сначала рассмотрим случай плоскопараллельного движения мяча до удара и после удара.

muτ + mvsinα = Sτ, mun +mvcosα=Sn,                          (14)

J(ωτ1 +ω0)=Sτr, где uτ,un - проекции скорости центра масс, ωτ - угловая скорость мяча в конце удара.

Коэффициент восстановления

u - w cos γ k = ⁿ

.

v cos α + w cos γ

Абсолютная скорость точки М равна при непроскальзывании wsinγ =uτ +ωτ r.(16)

Система уравнений (14) – (16) имеет решение

232 u = wsinγ - vsinα+ ω r, τ5          55

un = (1+k)wcosγ+kvcosα,(17)

3w      3v2

ω = sin γ+ sin α- ω .

τ1 5 r         5 r5 которое при v = 0, ω0 = 0 совпадает с решением (7).

При проскальзывании мяча, когда условие непроскальзывания

S τ <  fS n

не выполняется, необходимо в системе уравнений (14) – (16) кинематическое уравнение (16) заменить силовым

S τ = fS n .

• 3.2.    Произвольное движение мяча. До удара мяч совершает сложное движение, состоящее из поступательного движения вместе с центром масс со скоростью v и, вообще говоря, сферического движения около центра масс с мгновенной угловой скоростью го 0 . Считается, что проекции этих векторов на оси декартовой системы координат 0 xyz , связанной с игровой площадкой, известны в момент начала удара. Положение точки удара М задано радиусом-вектором r , проведенным из центра масс мяча, а также задана скорость удара w .

Скорость центра масс мяча u в конце удара и угловая скорость го могут быть определены с помощью решения, полученного для плоскопараллельного движения.

Для этого нужно, прежде всего, задать положение ударной плоскости в декартовой системе координат. Ударную плоскость определим как плоскость, в которой лежат вектор относительной скорости удара

—* —* —* —* —* w1 = w - v -ю0 х r и единичный вектор нормали n = - r I r, где r - радиус-вектор, проведенный из центра сферы в точку удара М.

Построим естественную систему координат Mn т 1 т в точке удара с ортами n , Т 1 , т ,

^—      ^—

• — w х n — — —

  
  

• т, = 1т, т = n хт.

1     ^{—    —}               1

I W 1 х n

Ось M т перпендикулярна ударной плоскости, а ось M т лежит в ней.

Предполагается, что вектор ударного импульса S лежит в ударной плоскости. Это основная гипотеза в методе решения задачи. В частных движениях мяча она легко подтверждается опытом, а для общего случая приведенное ниже решение нужно сравнивать с результатами эксперимента.

В случае непроскальзывания в решении (17), полученном для плоскопараллельного движения, надо сделать некоторые изменения. Скорости w , v и ю ₀ нужно заменить на проекции векторов w , v и со ₀ на ударную плоскость Mn т и ось M q, соответственно:

— —— — ^ — w = (w • n)n + (w -т)т ,                            (23)

— ——  /— —\— v = (v • n)n + (v • т)т ,                                (24)

—— ю0 =ю0 ^т1.

Углы γ и α в (17) заменяются углами