Ударная волна в газовом шаре
Автор: Куропатенко Валентин Федорович, Шестаковская Елена Сергеевна, Якимова Марина Николаевна
Рубрика: Математическое моделирование
Статья в выпуске: 1 т.9, 2016 года.
Бесплатный доступ
Математическое моделирование широко применяется для исследований во всех естественных науках, в отраслях промышленности, в экономике, биологии и других областях. Для решения конкретных задач используются уже существующие или создаются новые модели и численные методы. Наиболее надежным способом проверки качества разностной схемы является сравнение численного решения, где это возможно, с точным решением задачи. В качестве такого эталонного решения построено точное решение задачи о сходящейся ударной волне и о динамическом сжатии газа, находящегося в сферическом сосуде с непроницаемой стенкой. В начальный момент времени наружная граница газа скачком начинает двигаться с отрицательной скоростью, и в газ от границы начинает распространяться ударная волна. Ускорение границы и сферичность определяют движение ударной волны и структуру течения газа между фронтом ударной волны и границей. Изложенная постановка задачи принципиально отличается от ранее известных постановок задачи о схождении автомодельной ударной волны к центру симметрии и ее отражении от центра, в которых отсутствует граница газа.
Ударная волна, аналитическое решение, идеальный газ, сферическая симметрия
Короткий адрес: https://sciup.org/147159356
IDR: 147159356 | УДК: 533.6.011.1 | DOI: 10.14529/mmp160101
Текст научной статьи Ударная волна в газовом шаре
1. Постановка задачи
Развитие теории размерности и подобия величин механики сплошной среды началось примерно в 1920 - 1930 гг. одновременно в Советском Союзе и за. рубежом. Эта. теория была использована для построения автомодельных решений задачи о фокусировке ударной волны (УВ) в идеальном газе с уравнением состояния
P = f ( s ) PY. (1)
Первой опубликованной работой была работа. Гудерлея [1], в которой предполагалось, что амплитуда. У В по мере ее приближения к центру симметрии неограниченно возрастает. Автомодельное решение задачи о сходящейся УВ было опубликовано Л.И. Седовым в 1945 г. [2] и К.П. Станюковичем в 1945 г. [3]. Обзор работ по фокусировке УВ и полостей в идеальном газе изложен в работе К.В. Брушлинского и Я.М. Каждана [4]. Все эти решения являются автомодельными. Они получены в рамках общей теории подобия и размерностей, построенной Л.14. Седовым [5]. В конце прошлого столетия появились работы А.Ф. Сидорова, и его учеников, посвященные построению автомодельных решений с безударным сжатием идеального газа [6]. Новые автомодельные решения для различных режимов безударного сжатия идеального газа и схлопывания сферической полости с образованием ударной волны получены А.Н. Крайко и его учениками [7]. В отличие от решений задачи о сходящейся УВ, в которых отсутствует граница газовой сферы, рассмотрим схождение ударной волны в газовом шаре с наружной границей. В момент t = t0 в газе давление P0 = 0, плотность р 0 = const, скор ость U0 = 0, удельная внутренняя энергия Е0 = 0. Граница газового шара находится в точке r0, t0 . На границе задана начальная скорость Ug0 < 0. Иными словами, на границе задан разрыв скорости. После распада разрыва в газ пойдет УВ. Граница при t > t0 будет двигаться по определенному закону, согласованному с движением У В.
2. Ударная волна
Сферически симметричная сходящаяся к центру ударная волна - это поверхность, движение которой определяется зависимостью r w ( t ). В случае распространения УВ по холодному покоящемуся идеальному газу с перечисленными выше параметрами условия на УВ имеют вид [8]
P w ( D — U w ) = р о D, P w = р о DU w , р о De w = P w U w , (2)
где e - удельная полная энергия, D - скорость У В. Индексом «0» обозначены величины перед УВ, индексом «w» - за УВ. В начальный момент времени t0 УВ выходит из точки r0, t0 со скоростью D0 , которая определяется скоростью границы шара Ug0. В момент фокусировки УВ tf ее координата rw(tf) равна нулю. Перечисленным условиям удовлетворяет уравнение траектории УВ rw = Г 0
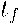 -t
t
f
- t
0
-t
t
f
- t
0
при n > 0. Скорость У В получаете -я дифференцированием rw
D =
r 0 n t f - t 0
t f -t n 1 .
t f - t 0
В момент фокусировки УВ при t = t f из-за сферичноети должно быть D = —то. Следовательно, показатель n должен удовлетворять условиям 0 < n < 1. При t = t 0 из (4) следует связь между r 0, 1 0, D 0 и n
D
о=
r 0 n t f - t 0
Поскольку величины r0, 10, D0 заданы при постановке задачи, то из (5) получается зависимость tf от показателя степени n tf
= t о —
r 0 n
D 0
а с помощью (5) выражение (4) принимает вид
D = D о
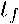 -t
t
0
-t
t
0
n - 1
В случае уравнения состояния идеального газа
P = ( y — 1) рЕ,
где E = 6 — 0 , 5 U 2, условия (2) на ударной волне упрощаются
Y + 1 тт 2
p w ~ 1 р 0 , U w । i D, P w р 0 DU w • (9)
При переходе от независимых термодинамических переменных р и E к переменным р и s давление принимает вид зависимости от энтропии и плотности (1). Подставив на ударной волне Pw и pw из (9) в (1), получим зависимость f (s) от скорости ударной волны f
Энтропия сохраняется вдоль траектории каждой частицы вещества, прошедшей через фронт ударной волны. Положение частицы меняется со временем, однако ее массовая координата m остается неизменной mw = 3 пр 0 rw • (И)
Поскольку D зависит от rw. то из (2). (7). (10) п (11) следует зависимость f ( m ) в газе за ударной волной, справедливая в любой момент времени, включая и момент фокусировки
Y 2(1 — n )
f ( s ) = Дт (ул) р 1-) D 0 ( m ) 3 n • 1121
3. Движение газа между ударной волной и границей
На фронте УВ газ приобретает скорость Uw < 0, поэтому в течение некоторого промежутка времени каждая частица движется к центру симметрии. Параметры течения газа определяются законом сохранения массы, уравнением движения и уравнением внутренней энергии др + и|р + р^ + 2^ = 0, + UY + т
∂t ∂r ∂r r ∂t ∂r ρ ∂r
% + ^ — + и|р
∂t ∂r ρ 2 ∂t ∂r
Для идеального газа (8) преобразуем это уравнение к виду dp + U^P + yP^ + 2U) =0 •
∂t ∂r ∂r r
Три уравнения (13), (14) содержат три характеристики движения газа P, р и U. Граничными условиями являются зависимости Pw (t), Uw (t) на ударной волне и Pg (t), Ug (t) на, границе газового шара. Для решепня (задачи перейдем от переменных r, t к новым переменным е(r,t), t. В результате такого перехода вместо уравнений (13), (14) будем рассматривать уравнения др + др де + и ар + дихде + ^ри = 0
∂t ∂ξ∂t ∂ξ ρ ∂ξ ∂r r ,
‘U + + GU. + 1 ТО =0 , (16)
∂t ∂ξ∂t ∂ξ ρ ∂ξ ∂r dP + ^ + (u^P + yP^) ^ =0. (17)
∂t ∂ξ ∂t ∂ξ ∂ξ ∂r r
Переменная .(r, t), выбирается следующим образом. Преобразуем уравнение траек тории ударной волны (3) так, чтобы комбинация rw и t была бы постоянной rw ()' = '■
В качестве . ( r,t ) возьмем такую функцию, чтобы она была бы постоянной на ударной волне. Проще всего взять ее в виде
. =
r tf - t0 n r0 tf - t .
На ударной волне r = rw и из (18), (19) следует, что .w = 1. Производные d. = rn /tf - tо\п d. = у /tf - tо д' r0 (tf — t) tf — t , dr r0 tf — t вместе co следующей из (19) зависимостью r(., t)
r = .r 0 ( f -; )
подставим в (15) -(17)
d p + n. d p + ( „эр + PdU ) 2. ( t f -t o)" + 2 pU ( f — ‘ о
∂t tf - t ∂ξ ∂ξ ∂ξ r0 tf - t r0ξ tf - t dU + ^LdU + fudU + 1 dP 1 n = o
∂t tf - t ∂ξ ∂ξ ρ ∂ξ r0 tf - t dP + ny dP + (,dP + Ypdu) у (tf-t ) n + 2YPU (‘fro) n = o.
∂t t f - t ∂ξ ∂ξ ∂ξ r 0 t f - t r 0 ξ t f - t
-
4. Разделение переменных
Согласно [8] будем искать решение системы уравнений (21) - (23) в виде
P = ар (t) П (.) ,р = ар (t) 5 (.), U = аи (t) M (.).(24)
Обозначим дифференцирование по t точкой сверху величины, дифференцирование по . - штрихом. Подставив (24) в (21) - (23), получим
Ф15 + ш.5 + M 5 + 5 M ‘ + 2м5 = 0, ф 25 M + шб. M ‘ + 5 MM ‘ + П ‘ = 0,(25)
Ф зП + ш. П ‘ + Mn ‘ + y nM ‘ + 2 y M^ = 0 ,
где
_ ар _ au a p n > at t f -t 0 n
Ф 1 = а Ф 2 = ав Ф 3 = а р в’ Ш = в ( t f - t ) ’ 9 = r 0 t f -1 ' "
Для разделения системы уравнений (25), (26) на две системы, одна из которых содержит величины, зависящие только от t , а вторая - только от £ , нужно, чтобы было
Ф 1 ( t ) = const ’ Ф 2 ( t ) = const ’ Ф 3 ( t ) = const ’ ш ( t ) = const .
Функции ар ( t ) ’ a u ( t ) , ap ( t ) определим на ударной волне. Предварительно преобразуем второе и третье уравнения (9) к виду
U w = ^ D t (т — ) ’ P w = Y -1 P w Y • (2S>
Y + 1 V f - 1 0/ 2
Из (24) и (28) на ударной волне следует
Y + 1
a P ( t ) ^ w p 0 ’ a u M w
Y - 1
2 D 0 ( t f - t ) - 1 1
Y + 1 U - 1 0) ’ “ p П
■ w 2 a p 5 w a u M w.
В этих уравнениях величины 5w, по аналогии с [2-4] примем, что
Mw 11 П w
не определены. Для устранения произвола
δ w
Y + 1
Y - 1 ’
M w
п w =Дт
Y + 1 Y + 1
.
При таком выборе 5w, Mw и П w , функции ар, аи и аР принимают вид
( t f - t 0 ) а р = P 0 , a u = D 0 t f - t J
t - t 2(1 - n )
’ “ p = P 0 D0 ("tf-t)
.
Из уравнений (27) и (30) определяются ф 1,
Ф 2- Ф 3 II Ш
n
Ф 1 = 0 , ф 2 = -
-
n
’ Ф 3 =
y n- 1 ,ш = - 1 . nn
-
5. Уравнения для M, д, Пи определение n
С помощью полученных значений ф 1, ф2, ф3 и ш уравнения (25) - (26) принимают вид дM‘ + (M - () д' = - 2M ’ д (M - ()M‘ + П‘ = - n—1 дM’(31)
ξn
YnM‘ + (M - ()П‘ = - 2yM^ - 2(n- 1) П.(32)
Уравнения (31), (32) образуют относительно д' , M ‘ , П ‘ систему линейных неоднородных уравнений. Если определитель этой системы
Z =(M - () (yП - д (M - ()2)(33)
не равен нулю, то система имеет единственное решение. Из (29) и (33) следует, что на ударной волне Z (1) = — )— < 0. В момент фокусировки £ = то й, следовательно, Z ( то ) = + то. если при £ ^ то M не стремится к + то кгяс £а. г,те а > 1. Посколь ку рассматривается газовый шар конечного размера и время фокусировки конечно, то естественно потребовать, чтобы M ^, П го и 5^ были бы конечны. Из сказанного следует, что существует такое значение £* при ко тором Z* = 0 и M, П, 5 принимают значения M * , П *, 5*. В областях 1 < £ < £* и £* < £ < то Z = 0 и в этих областях, как сказано выше, система уравнений (31), (32) имеет единственное решение. В точке же £* следует рассмотреть м;отрину коэффициентов | |A | | п расширенную матрицу | |B||.
где
И A | | =
5* M * — £*
5* (M * — £* ) 0
7 П * 0
(M * — £* )
|
5* M * — £* | |B | | = 5* (M * — £* ) 0 7 П * 0 |
0 _ 2M * 8 , ^ * 1 — n - 1 5* M * (M * — £* ) — 2П * jM“ + n - 1) |
Анализ матриц | | A | | и | |B | | показывает, что их ранги совпадают и равны 2, все миноры третьего порядка равны нулю и, следовательно, система (31), (32) при £ = £* имеет единственное решение. Легко показать, что равенство нулю всех миноров третьего порядка приводит к двум уравнениям
( n — 1) £* (2 (M * — £* ) — Y M * ) + 2 Yn M * (M * — £* ) = 0 , (34)
Z* = (M * — £* ) ( Y П * — 5* (M * — £* )2) = 0 , (35) содержащим n, 7 и величины M * , П *, 5*, £*, зависящие от n и 7 . Из уравнений (34) и (35) для каждого значения 7 находится соответствующее значение n . Результатом применения изложенной выше процедуры являются значения n ( 7 ), которые приведены в табл. 1.
Таблица 1
|
γ |
n |
ρ f |
t f |
|
1,1 |
0,795973 |
184,465 |
0,758066 |
|
1,2 |
0,757142 |
59,5525 |
0,688311 |
|
4/3 |
0,729259 |
26,5447 |
0,625079 |
|
1,4 |
0,717175 |
20,0714 |
0,5976454 |
|
5/3 |
0,688377 |
9,54968 |
0,5162826 |
В областях, где Z = 0, выпишем решение системы уравнений (31), (32)
|
M ' = Rm- , ξnR , |
., 5H6 5 ( £ — M) R n 5 = n£ (M — £ ) R’ П= n£R ' (3G> |
|
где |
R = y П — 5 (M — £ )2 , (37) |
R м = 2 ( n - 1) ( П + 2 Yn МП + ( n - 1) (5 M (M - ( ) ,
Rs — R м — 2 n M R, R n — R м — -— --
Функции M( ( ), 5 ( ( ), П( ( ), находятся при определенном значении п путем интегрирования уравнений (36) в области 1 < ( < то.
6. Решение
Для практических применений полученного решения нужно перейти от функций M( ( ), 5 ( ( ), П( ( ) к функциям U ( r, t ), р ( r, t ), P ( r, t ), характеризующим состояние и движение газа в переменных r, t . Они получаются из уравнений (24) следующим образом. В любой фиксированный момент времени t 0 < t < t f из (19) получается однозначная зависимость ( ( r ), после чего из уравнений (24) вычисляются
2(1 - n )
• (40)
U ( r,t ) — D 0 M( ( ( r,t )) ( f — ?) . P ( r,t )— р 0 D 0П( ( ( r,t )) f —г)
P ( r,t )— P о 5 ( ( ( r,t )) • (41)
Эти функции вычисляются в области rw < r < rg , занятой газ ом в момент t. Безразмерная координата границы газового шара (g в момент t находится из закона сохранения массы rg
14 nr2 р (r) dr — 3 про (r0 — rW) , rw который в переменных t, ( принимает вид
ξ g
/ 5( 2 d( — 3 ((1 —
( t— t о> D о ) " 3 ” — Л—0 .
r 0 n
Затем по найденному значению ( g для фиксированного t из (19) находится r g ( t ), а из зависимостей M ( ( ) п П ( ( ) определяются M g i1 П g. по которым из (24) находятся U g ( t ) ii P g ( t ). Таким образом, получаются табличные зависимости U g ( t ). P g ( t ) , r g ( t ).
7. Фокусировка ударной волны
Момент фокусировки ударной волны tf находится из (6) Ugо- rо- 10. Y- Dо — дтUgо- и па!Ueno n(y)• Для rо — 1. Ugо после того, как заданы — — 1. tо — 0 значения
времени фокусировки для разных y приведены в Табл. 1. В точке t — t f, r w — 0 находится ударная волна, за фронтом которой D — —то, U w — —то, P w — то, рw — ^^ + ^ 1, (w — 1. Из (19) следует, что при любом r > 0 значению t — t f соответствует значение ( — то. При интегрировании у равнений (36) значению ( — то соответствуют значения 5^- M ^. П ^. которые постоянны, т.к. из (36) - (39) следует, что 5' ^ 0. M ‘ ^ 0. П ‘ ^ 0 при ( ^ то. Из выраже!шй (30) для au. ар виднс). что аи — —то. ар — то njш t — t f п выражения для U и P принимают вид
U f — —то M ю, P f — то П ^.
Работа, совершенная над газовым шаром за время 0 < t < tf , конечна. Это значит, что и кинетическая, и внутренняя энергия газа в шаре конечны. Таким образом, чтобы скорость U и давление Р газа в момент фокусировки имели физически разумные значения (были ограничены), должно быть M го = 0 и П го = 0, ибо только в этом случае U й P можно получить, раскрыв в (24) неопределенности вида ( то • 0). Численное интегрирование уравнений (36) дает с высокой точностью именно такие значения M ^ = 0 и П ^ = 0. Конечно, значению £ = то соответствует много значений г. Но если взять t = t f — т , где т бесконечно малое число, то £ = то получается из (19) только при r = то . В этом случае из (40) следует, что в момент фокусировки
U^ = 0 , P^ = 0 , при , r = то.
Функции U ( r ) и P ( r ) при t = t f должны удовлетворять этим асимптотическим условиям. Из функций ар, au, ар (30) только ар = const. Таким образом, в момент фокусировки t f во всем газовом шаре в соответствии с (41)
P f = Р о 5Ю = const .
Значения pf , полученные для разных у , приведены в табл. 1. Профиль давления в момент фокусировки определим, используя зависимость энтропии от массы (12). Подставив f ( s ) из (12) и p f из (43) в уравнение состояния (1), получим
P ( r ) =
2 _2
Y +1 Р 0 D 0
Y — 1 7 / Y - ^ )
Y + 1)
r 0
2(1 — n ) n
Эта зависимость справедлива для всего газа, лежащего в промежутке 0 < r < rg. Формально ее можно считать справедливой и в области r > rg, т.е. вне газового шара. Это можно использовать для подтверждения изложенных выше результатов интегрирования. Действительно, из (44) следует, что Р^ = 0 пр и r = то. Удельная внутренняя энергия определяется из уравнений (8) и (44)
2(1 n ) 2(1 — n )
E ( r ) = 2 D 2 ( y — 1) Y- 1 ( Y + 1) - ( Y +1) C 1 - (r °) . (45)
Полная внутренняя энергия газового шара получается с помощью (45) в виде rg
Q E=/
4 nr 2 p о d^E ( r ) dr.
Работа, совершенная над газовым шаром на его границе, определяется уравнением
A =
t f
J 4 nr g ( t ) P g ( t ) U g ( t ) dt.
Следовательно, кинетическая энергия газа в момент фокусировки должна опреде
ляться выражением
r gf
Q k = A — Q e = У 2 nr 2 p f U 2 ( r ) dr.
Рассмотрим решение в момент времени t = t f — т (т - бесконечно малое число). С помощью (19) запишем (40) так
U = D о
1 - n
( V ) " М( « ) •
При t ^ t f представим зависимость М( £ ) в виде
М( ( ) = B ( ,
где B = const. Эта зависимость удовлетворяет выше сформулированному требованию М ^ = 0 пр и £ = то . Из (47), (48) следует зависимость скорости от радиуса в момент t очень близкий к фокусировке
1 - n
U = D о ( ’ ) B.
Постоянная B находится после подстановки (49) в (46) по формуле
B =
(5 n — 2) Q k
2(1 - n ) 5 n - 2
2 nnD 2 p f r 0 n r gf n
8. Эталонное решение
Изложенное решение было применено для оценки точности нескольких методов расчета ударных волн. Холодный газовый шар размером r g 0 = 1 имел параметры P 0 = 0, p о = 1, U о = 0, U g о = — 1, Y = 5 / 3. Граничное условие определялось с помощью уравнения (42) в соответствии с описанным в п. 6 алгоритмом. Зависимости давления и скорости границы от времени приведены в табл. 2. На рис. 1, 2, 3 приведены профили давления, плотности и скорости на три момента времени t = 0 , 4, t = 0 , 45 и t = 0 , 5. Сплошная линия - это аналитическое решение данной работы, -о— это расчеты по программе ВОЛНА [9] с выделением разрывов,-----расчеты по программе ВОЛНА без выделения разрывов, х - результаты, полученные при проведении расчета по методике [10]. Расчеты выполнены на равномерной по r сетке
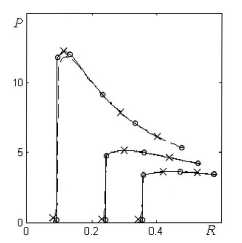
Рис. 1. Профили давления
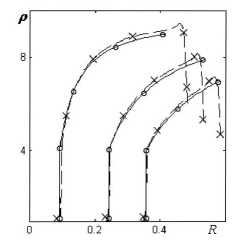
Рис. 2. Профили плотности
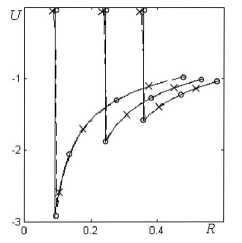
Рис. 3. Профили скорости
Таблица 2
Граничное условие
В табл. 3, 4 и 5 приведены зависимости U ( r ), р ( r ), P ( r ), полученные из аналитического решения, на моменты времени t = 0 , 4, t = 0 , 45, t = 0 , 5, соответственно. В табл. 6 приведены аналитические зависимости М( С ), П( С ) и 6 ( С ) в диапазоне 1 < С А 10. Для того, чтобы построить решение U ( r ). р ( r ). P ( r ) в любой выбран ный момент времени t* , задаем С из табл. 6 и находим r из формулы (19), затем по формулам (40) и (41) вычисляем U ( r ), р ( r ), P ( r ).
Таблица 3
Аналитическое решение на момент t = 0 , 4
|
№ |
r |
P ( r ) |
р ( r ) |
U ( r ) |
№ |
r |
P ( r ) |
р ( r ) |
U ( r ) |
|
1 |
0,3584 |
3,3761 |
4,0000 |
- 1,5912 |
24 |
0,4660 |
3,5944 |
5,9404 |
- 1,2335 |
|
2 |
0,3631 |
3,4043 |
4,1303 |
- 1,5681 |
25 |
0,4706 |
3,5912 |
5,9954 |
- 1,2232 |
|
3 |
0,3678 |
3,4299 |
4,2533 |
- 1,5460 |
26 |
0,4753 |
3,5874 |
6,0488 |
- 1,2132 |
|
4 |
0,3724 |
3,4533 |
4,3698 |
- 1,5249 |
27 |
0,4800 |
3,5831 |
6,1009 |
- 1,2034 |
|
5 |
0,3771 |
3,4744 |
4,4806 |
- 1,5047 |
28 |
0,4847 |
3,5783 |
6,1515 |
- 1,1938 |
|
6 |
0,3818 |
3,4935 |
4,5863 |
- 1,4854 |
29 |
0,4894 |
3,5730 |
6,2009 |
- 1,1845 |
|
7 |
0,3865 |
3,5106 |
4,6873 |
- 1,4668 |
30 |
0,4940 |
3,5672 |
6,2490 |
- 1,1755 |
|
8 |
0,3911 |
3,5258 |
4,7840 |
- 1,4489 |
31 |
0,4987 |
3,5611 |
6,2959 |
- 1,1666 |
|
9 |
0,3958 |
3,5394 |
4,8768 |
- 1,4318 |
32 |
0,5034 |
3,5545 |
6,3416 |
- 1,1579 |
|
10 |
0,4005 |
3,5513 |
4,9661 |
- 1,4153 |
33 |
0,5081 |
3,5476 |
6,3861 |
- 1,1495 |
Окончание таблицы 3
|
№ |
r |
P ( r ) |
Р ( r ) |
U ( r ) |
№ |
r |
P ( r ) |
Р ( r ) |
U ( r ) |
|
11 |
0,4052 |
3,5616 |
5,0519 |
- 1,3993 |
34 |
0,5127 |
3,5403 |
6,4296 |
- 1,1412 |
|
12 |
0,4098 |
3,5706 |
5,1347 |
- 1,3840 |
35 |
0,5174 |
3,5328 |
6,4721 |
- 1,1332 |
|
13 |
0,4145 |
3,5782 |
5,2145 |
- 1,3691 |
36 |
0,5221 |
3,5249 |
6,5136 |
- 1,1253 |
|
14 |
0,4192 |
3,5846 |
5,2915 |
- 1,3548 |
37 |
0,5268 |
3,5167 |
6,5540 |
- 1,1176 |
|
15 |
0,4239 |
3,5898 |
5,3660 |
- 1,3409 |
38 |
0,5314 |
3,5083 |
6,5936 |
- 1,1100 |
|
16 |
0,4286 |
3,5939 |
5,4380 |
- 1,3275 |
39 |
0,5361 |
3,4997 |
6,6322 |
- 1,1026 |
|
17 |
0,4332 |
3,5969 |
5,5078 |
- 1,3145 |
40 |
0,5408 |
3,4908 |
6,6700 |
- 1,0954 |
|
18 |
0,4379 |
3,5990 |
5,5753 |
- 1,3019 |
41 |
0,5455 |
3,4817 |
6,7069 |
- 1,0883 |
|
19 |
0,4426 |
3,6002 |
5,64078 |
- 1,2897 |
42 |
0,5502 |
3,4724 |
6,7430 |
- 1,0814 |
|
20 |
0,4473 |
3,6005 |
5,7043 |
- 1,2778 |
43 |
0,5548 |
3,4630 |
6,7783 |
- 1,0746 |
|
21 |
0,4519 |
3,6001 |
5,7659 |
- 1,2662 |
44 |
0,5595 |
3,4533 |
6,8128 |
- 1,0679 |
|
22 |
0,4566 |
3,5989 |
5,8258 |
- 1,2550 |
45 |
0,5876 |
3,3927 |
7,0053 |
- 1,0305 |
|
23 |
0,4613 |
3,5969 |
5,8839 |
- 1,2441 |
Таблица 4
Аналитическое решение на момент t = 0 , 45
|
№ |
r |
P ( r ) |
Р ( r ) |
U ( r ) |
№ |
r |
P ( r ) |
Р ( r ) |
U ( r ) |
|
1 |
0,2434 |
4,7924 |
4,0000 |
- 1,8959 |
24 |
0,3810 |
4,8977 |
6,8237 |
- 1,2698 |
|
2 |
0,2494 |
4,8648 |
4,2393 |
- 1,8450 |
25 |
0,3870 |
4,8712 |
6,8863 |
- 1,2554 |
|
3 |
0,2554 |
4,9253 |
4,4553 |
- 1,7983 |
26 |
0,3930 |
4,8441 |
6,9465 |
- 1,2415 |
|
4 |
0,2613 |
4,9752 |
4,6525 |
- 1,7552 |
27 |
0,3989 |
4,8165 |
7,0044 |
- 1,2280 |
|
5 |
0,2673 |
5,0156 |
4,8340 |
- 1,7153 |
28 |
0,4049 |
4,7883 |
7,0600 |
- 1,2150 |
|
6 |
0,2733 |
5,0475 |
5,0023 |
- 1,6782 |
29 |
0,4109 |
4,7598 |
7,1136 |
- 1,2025 |
|
7 |
0,2793 |
5,0720 |
5,1590 |
- 1,6435 |
30 |
0,4169 |
4,7310 |
7,1653 |
- 1,1903 |
|
8 |
0,2853 |
5,0899 |
5,3054 |
- 1,6111 |
31 |
0,4229 |
4,7018 |
7,2150 |
- 1,1785 |
|
9 |
0,2913 |
5,1019 |
5,4428 |
- 1,5806 |
32 |
0,4289 |
4,6725 |
7,2631 |
- 1,1671 |
|
10 |
0,2972 |
5,1088 |
5,5721 |
- 1,5518 |
33 |
0,4348 |
4,6431 |
7,3094 |
- 1,1561 |
|
11 |
0,3032 |
5,1111 |
5,6939 |
- 1,5247 |
34 |
0,4408 |
4,6135 |
7,3541 |
- 1,1454 |
|
12 |
0,3092 |
5,1093 |
5,8091 |
- 1,4990 |
35 |
0,4468 |
4,5839 |
7,3974 |
- 1,1350 |
|
13 |
0,3152 |
5,1039 |
5,9181 |
- 1,4747 |
36 |
0,4528 |
4,5542 |
7,4392 |
- 1,1249 |
|
14 |
0,3212 |
5,0953 |
6,0215 |
- 1,4515 |
37 |
0,4588 |
4,5245 |
7,4796 |
- 1,1151 |
|
15 |
0,3272 |
5,0838 |
6,1197 |
- 1,4295 |
38 |
0,4647 |
4,4949 |
7,5187 |
- 1,1055 |
|
16 |
0,3331 |
5,0699 |
6,2131 |
- 1,4085 |
39 |
0,4707 |
4,4653 |
7,5566 |
- 1,0962 |
|
17 |
0,3391 |
5,0538 |
6,3021 |
- 1,3885 |
40 |
0,4767 |
4,4358 |
7,5933 |
- 1,0872 |
|
18 |
0,3451 |
5,0357 |
6,3870 |
- 1,3694 |
41 |
0,4827 |
4,4065 |
7,6288 |
- 1,0784 |
|
19 |
0,3511 |
5,0159 |
6,4680 |
- 1,3510 |
42 |
0,4887 |
4,3772 |
7,6633 |
- 1,0698 |
|
20 |
0,3571 |
4,9946 |
6,5454 |
- 1,3335 |
43 |
0,4947 |
4,3481 |
7,6967 |
- 1,0615 |
|
21 |
0,3630 |
4,9720 |
6,6195 |
- 1,3166 |
44 |
0,5006 |
4,3192 |
7,7291 |
- 1,0533 |
|
22 |
0,3690 |
4,9482 |
6,6905 |
- 1,3004 |
45 |
0,5365 |
4,1495 |
7,9048 |
- 1,0084 |
|
23 |
0,3750 |
4,9234 |
6,7585 |
- 1,2848 |
Таблица 5
Аналитическое решение на момент t = 0 , 5
|
№ |
r |
P ( r ) |
P ( r ) |
U ( r ) |
№ |
r |
P ( r ) |
P ( r ) |
U ( r ) |
|
1 |
0,0926 |
11,4956 |
4,0000 |
- 2,9363 |
24 |
0,2777 |
8,1137 |
8,5003 |
- 1,3032 |
|
2 |
0,1007 |
11,9886 |
4,7516 |
- 2,6848 |
25 |
0,2858 |
7,9479 |
8,5430 |
- 1,2826 |
|
3 |
0,1087 |
12,2118 |
5,3157 |
- 2,4917 |
26 |
0,2938 |
7,7882 |
8,5829 |
- 1,2630 |
|
4 |
0,1168 |
12,2584 |
5,7648 |
- 2,3370 |
27 |
0,3019 |
7,6343 |
8,6202 |
- 1,2444 |
|
5 |
0,1248 |
12,1902 |
6,1336 |
- 2,2092 |
28 |
0,3099 |
7,4862 |
8,6552 |
- 1,2267 |
|
6 |
0,1328 |
12,0473 |
6,4426 |
- 2,1014 |
29 |
0,3180 |
7,3433 |
8,6879 |
- 1,2097 |
|
7 |
0,1409 |
11,8565 |
6,7055 |
- 2,0087 |
30 |
0,3260 |
7,2056 |
8,7187 |
- 1,1936 |
|
8 |
0,1489 |
11,6358 |
6,9319 |
- 1,9280 |
31 |
0,3341 |
7,0728 |
8,7477 |
- 1,1781 |
|
9 |
0,1570 |
11,3974 |
7,1288 |
- 1,8568 |
32 |
0,3421 |
6,9447 |
8,7750 |
- 1,1632 |
|
10 |
0,1650 |
11,1497 |
7,3015 |
- 1,7935 |
33 |
0,3502 |
6,8209 |
8,8007 |
- 1,1489 |
|
11 |
0,1731 |
10,8984 |
7,4540 |
- 1,7366 |
34 |
0,3582 |
6,7015 |
8,8251 |
- 1,1352 |
|
12 |
0,1811 |
10,6474 |
7,5896 |
- 1,6852 |
35 |
0,3663 |
6,5861 |
8,8481 |
- 1,1221 |
|
13 |
0,1892 |
10,3996 |
7,7109 |
- 1,6384 |
36 |
0,3743 |
6,4745 |
8,8699 |
- 1,1094 |
|
14 |
0,1972 |
10,1567 |
7,8199 |
- 1,5956 |
37 |
0,3824 |
6,3666 |
8,8906 |
- 1,0971 |
|
15 |
0,2053 |
9,9198 |
7,9184 |
- 1,5563 |
38 |
0,3904 |
6,2622 |
8,9103 |
- 1,0854 |
|
16 |
0,2133 |
9,6898 |
8,0076 |
- 1,5199 |
39 |
0,3985 |
6,1612 |
8,9290 |
- 1,0740 |
|
17 |
0,2214 |
9,4670 |
8,0889 |
- 1,4862 |
40 |
0,4065 |
6,0634 |
8,9468 |
- 1,0630 |
|
18 |
0,2294 |
9,2517 |
8,1632 |
- 1,4548 |
41 |
0,4146 |
5,9686 |
8,9637 |
- 1,0523 |
|
19 |
0,2375 |
9,0439 |
8,2312 |
- 1,4254 |
42 |
0,4226 |
5,8768 |
8,9799 |
- 1,0420 |
|
20 |
0,2455 |
8,8437 |
8,2938 |
- 1,3980 |
43 |
0,4307 |
5,7878 |
8,9953 |
- 1,0320 |
|
21 |
0,2536 |
8,6507 |
8,3515 |
- 1,3722 |
44 |
0,4387 |
5,7014 |
9,0100 |
- 1,0224 |
|
22 |
0,2616 |
8,4649 |
8,4049 |
- 1,3478 |
45 |
0,4870 |
5,2335 |
9,0860 |
- 0,9700 |
|
23 |
0,2697 |
8,2860 |
8,4543 |
- 1,3249 |
Таблица 6
Аналитическое решение
|
№ |
ξ |
n( ( ) |
5 ( ( ) |
M( ( ) |
№ |
ξ |
n( ( ) |
5 ( ( ) |
M( ( ) |
|
1 |
1,000 |
0,7500 |
4,0000 |
0,7500 |
24 |
1,828 |
0,7188 |
7,3840 |
0,4503 |
|
2 |
1,036 |
0,7660 |
4,3422 |
0,7211 |
25 |
1,864 |
0,7120 |
7,4454 |
0,4444 |
|
3 |
1,072 |
0,7781 |
4,6391 |
0,6955 |
26 |
1,900 |
0,7052 |
7,5039 |
0,4388 |
|
4 |
1,108 |
0,7870 |
4,9018 |
0,6727 |
27 |
1,936 |
0,6984 |
7,5597 |
0,4334 |
|
5 |
1,144 |
0,7933 |
5,1375 |
0,6521 |
28 |
1,972 |
0,6917 |
7,6129 |
0,4282 |
|
6 |
1,180 |
0,7973 |
5,3508 |
0,6334 |
29 |
2,296 |
0,6335 |
8,0000 |
0,3890 |
|
7 |
1,216 |
0,7993 |
5,5453 |
0,6163 |
30 |
2,620 |
0,5816 |
8,2718 |
0,3596 |
|
8 |
1,252 |
0,7999 |
5,7236 |
0,6005 |
31 |
2,944 |
0,5364 |
8,4716 |
0,3363 |
|
9 |
1,288 |
0,7990 |
5,8879 |
0,5860 |
32 |
3,268 |
0,4972 |
8,6236 |
0,3174 |
|
10 |
1,324 |
0,7971 |
6,0398 |
0,5726 |
33 |
3,592 |
0,4630 |
8,7426 |
0,3016 |
|
11 |
1,360 |
0,7942 |
6,1807 |
0,5601 |
34 |
3,916 |
0,4330 |
8,8379 |
0,2881 |
|
12 |
1,396 |
0,7906 |
6,3118 |
0,5484 |
35 |
4,240 |
0,4067 |
8,9156 |
0,2764 |
|
13 |
1,432 |
0,7863 |
6,4341 |
0,5375 |
36 |
4,564 |
0,3834 |
8,9799 |
0,2661 |
Окончание таблицы 6
|
14 |
1,468 |
0,7815 |
6,5485 |
0,5272 |
37 |
4,888 |
0,3626 |
9,0340 |
0,2570 |
|
15 |
1,504 |
0,7762 |
6,6558 |
0,5176 |
38 |
5,212 |
0,3440 |
9,0800 |
0,2489 |
|
16 |
1,540 |
0,7706 |
6,7565 |
0,5085 |
39 |
5,536 |
0,3272 |
9,1193 |
0,2415 |
|
17 |
1,576 |
0,7647 |
6,8513 |
0,4998 |
40 |
5,860 |
0,3120 |
9,1535 |
0,2348 |
|
18 |
1,612 |
0,7585 |
6,9406 |
0,4917 |
41 |
6,832 |
0,2741 |
9,2326 |
0,2178 |
|
19 |
1,648 |
0,7522 |
7,0249 |
0,4839 |
42 |
7,804 |
0,2445 |
9,2883 |
0,2043 |
|
20 |
1,684 |
0,7457 |
7,1046 |
0,4765 |
43 |
8,776 |
0,2209 |
9,3293 |
0,1931 |
|
21 |
1,720 |
0,7390 |
7,1801 |
0,4695 |
44 |
9,748 |
0,2016 |
9,3605 |
0,1838 |
|
22 |
1,756 |
0,7323 |
7,2516 |
0,4628 |
45 |
10,00 |
0,1971 |
9,3674 |
0,1816 |
|
23 |
1,792 |
0,7256 |
7,3195 |
0,4564 |
Работа проводилась при финансовой поддержке РФФИ. Грант 13-01-00072.
Список литературы Ударная волна в газовом шаре
- Guderley, G. Starke kugelige und zylindrische Verdichtungsstobe in der Nahe des Kugelmittelpunktes bzw. der Zylinderachse/G. Guderley//Luftfartforschung. -1942. -Т. 19, № 9. -С. 302-312.
- Седов, Л.И. О неустановившихся движениях сжимаемой жидкости/Л.И. Седов//Доклады Академии наук СССР. -1945. -Т. 47, № 2. -С. 94-96.
- Станюкович, К.П. Автомодельные решения уравнений гидромеханики, обладающих центральной симметрии/К.П. Станюкович//Доклады Академии наук СССР. -1945. -Т. 48, № 5. -С. 331-333.
- Брушлинский, К.В. Об автомодельных решениях некоторых задач газовой динамики/К.В. Брушлинский, Я.М. Каждан//Успехи математических наук. -1963. -Т. 18, № 2. -С. 3-23.
- Седов, Л.И. Методы подобия и размерности в механике/Л.И. Седов. -М.: Тех. теор. лит., 1954.
- Сидоров, А.Ф. Процессы безударного конического сжатия и разлета газа/А.Ф. Сидоров, О.Б. Хайруллина//Прикладная математика и механика. -1994. -Т. 58, № 4. -С. 81-92.
- Крайко, А.Н. Быстрое цилиндрически и сферически симметричное сильное сжатие идеального газа/А.Н. Крайко//Прикладная математика и механика. -2007. -Т. 71, № 5. -С. 744-760.
- Куропатенко, В.Ф. Модели механики сплошных сред/В.Ф. Куропатенко. -Челябинск: ЧелГУ, 2007.
- Куропатенко, В.Ф. Комплекс программ ВОЛНА и неоднородный разностный метод расчета неустановившихся движений сжимаемых сплошных сред/В.Ф. Куропатенко, В.И. Кузнецова, Г.Н. Михайлова, Г.В. Коваленко, Г.Н. Сапожникова//Вопросы атомной науки и техники. Серия: Математическое моделирование физических процессов. -1989. -№ 2. -С. 9-25.
- Kuropatenko, V.F. A Method for Shock Calculation/V.F. Kuropatenko, M.N. Yakimova//Journal of Computational and Engineering Mathematics. -2015. -V. 2, № 2. -P. 60-70.


