Удвоенное обращение волнового фронта при шестиволновом взаимодействии на тепловой нелинейности

Наряду с четырехволновым взаимодействием для получения волны с обращенным волновым фронтом может быть использовано шестиволновое взаимодействие. Переход от четырех- к шестиволновым взаимодействиям расширяет возможности управления параметрами отраженной (объектной) волны, позволяет, в частности, получить волну с удвоенным обращенным волновым фронтом [1; 2].

При реализации шестиволновых взаимодействий, как правило, рассматриваются среды с резонансной нелинейностью, в которых за счет подбора частот взаимодействующих волн можно существенно повысить коэффициент отражения шестиволновых преобразователей излучения [3–6]. В последние годы выполнены работы по высокоэффективному шестиволновому преобразованию излучения с удвоенным обращением волнового фронта на тепловой нелинейности в линейно поглощающих средах [7; 8].

При практическом использовании шестиволновых преобразователей излучения в системах коррекции фазовых искажений, системах обработки и преобразования изображения необходимо знать, насколько точно волновой фронт объектной волны соответствует сопряженному (удвоенно сопряженному) волновому фронту обращенной (сигнальной) волны. К настоящему времени этот вопрос исследован лишь для шестиволнового преобразователя на керровской нелинейности [2; 9]. Представляет практический интерес изучение качества обращения волнового фронта при шестиволновом взаимодействии на других типах нелинейности, в частности, на тепловой нелинейности.

1. Пространственная селективность шестиволнового преобразователя

Рассмотрим типичную схему взаимодействия волн, позволяющую получить волну с удвоенным обращенным волновым фронтом. В плоском слое линейно поглощающей среды толщиной £ распространяются навстречу друг другу две волны накачки с комплексными амплитудами A ₁ и ^ 2 , частотами to 1 и ® 2 и сигнальная волна с амплитудой A 3 , частотой е> 1 (рис. 1).

Распространение излучения в поглощающей среде приводит к изменению температуры среды (5 T ), а значит, к изменению показателя преломления (5 n ). При малом изменении показателя преломления (5 n <<  n 0 ) выражение для квадрата показателя преломления можно записать следующим образом:

„2   „2 -1. ² dn XT ¹ d 2 n X ф2

n = n _n< 1 +----- 5 T +--- _ 5 T

⁰ I     n 0 dT 2 dT ²

Здесь n ₀ – среднее значение показателя преломления.

В приближении заданного поля по волнам накачки (| A12I >> A3 41) , с учетом интерференции сигнальной волны с первой волной накачки, вы- ражение для интенсивности волн в нелинейной среде есть i = i о + Ai a3 + a; A3, где I0 = I1 + I2 , I1,2 = A1,2Al,2 .

Тогда изменение температуры можно представить в виде суммы медленно (5 Т 0 ) и быстро (5 7 31 ) меняющихся в зависимости от координат составляющих:

5 Т = 5 7 0 + 5 7 31 + 5 Т 31* .

Здесь 5 Т 31 — изменение температуры, обусловленное интерференцией волны накачки и сигнальной волны.

За шестиволновое взаимодействие отвечают квадратичные температурные решетки, вклад которых в изменение показателя преломления определяется слагаемым dn 5 Т dT2

Дифракция второй волны накачки на квадратичной температурной решетке (5 7 31 ) приводит к возникновению объектной волны с удвоенным обращенным волновым фронтом на частоте © 2 = © 1 + © 1 + © 2 - © 1 - © 1 с комплексной амплитудой

A ₆

—■

dn 2

—- ^{5 Т} 31 A 2 , dT ₂    31 2

распространяющейся навстречу сигнальной волне.

С учетом указанных выше приближений, при условии малого коэффициента отражения (|Аб| << Аз|), уравнение Гельмгольца, описывающие шестиволновое взаимодействие в среде с те- пловой нелинейностью, распадается на четыре уравнения [10]:

V² + /

1 + А- ( n io

dn 5 Т₀

dT ⁰

^{- 2} ik i ^a i ^ A 1,3 = 0,

Г          (9

L2 + / 2 1 +---

I          I

- 2ik2a2 \ A2 = 0, dn 5 7

dT ⁰

1 d ² n   2

+ 7"----9" 5 1q

2 dT ^{2   0}

А

-

V² + k 2

n ₂₀

dn 5 7

dT ⁰

, ¹ d ² n х m21

⁺ 7"---9" ⁵ А)

2 ат20

-

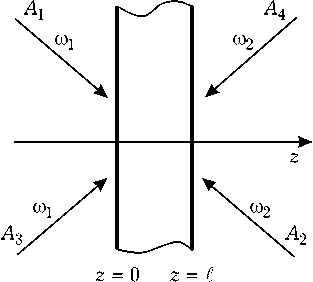
Рис. 1. Схема взаимодействия

Здесь к 12 = © 12 П 20 / c , ^а 12 и n 20 — коэффициент поглощения и показатель преломления на частоте © 12 .

Уравнения (1) дополняются уравнением Пуассона рии взаимодействия, система уравнений (1) пе-

странственного спектра объектной волны на передней грани нелинейного слоя есть

репишется следующим образом:

d^A 123 + Дк^ dz     n 10	dn 5 T dT	- +2 dT (5 T 0 )2.		"A 1,3 +
+ a 1 A 1,3 = 0, г d^A 2 - i j k^	d. 5 T	, 1 d 2 n T x2 + 2 dT 2(5 T 0) J , 1 d 2 n T x2 + 2 dT 2 (5 T 0) _ ^A 2 ( z ) x		*w ^2 -
dz    n 20 [ -a 2 A 2=0, d^A 6 - i k2	dT 0 dn 6 T			*w 4 6 -
dz    n20 k a 2 A6 i 2 n	dT 0 2 d 2 n 20 dT 2

ю

5 ^T 31 ^(к 1 т > ^z ) 8 7 31 ^(к t = ^к 6 ^{- к} 2 - ^к i t > ^z ) ^x

A 6 ( ^к 6 , ^z = 0 ) = i^"d-nAA 20 exp ^{[- С} 2 ( ^£ ) ] ^x 2 n 0 dT ²

£ ю xJJ5 T31 (к T1, z )x                              (6)

0 -ю x 5T31 (кT = к6 - к2 - кT1, z) x x exp [-i (k2z - k4z) z J dкт 1 dz .

Уравнение, описывающее изменение пространственного спектра быстро меняющейся в пространстве составляющей температуры, имеет вид

-I

' _ d 2_

₄ dz z^

)

^{- к} T ^{5 T} 31

+

-ю

^x exp [- i ( k 2z ^- к б z ) z J d к 1 т = 0.

+ ^a 1 " A 10" A 30 ^{exp [-} i ^{( k} 1 z ^{- k} 3 z ) ^{z - 2a} 1 ^z J = 0

^Л c p ^v

Уравнение Пуассона распадается на два урав-

нения:

V 2 5 T ₀ + ^а 1 ^{1 1 + а} 2 I ² = 0, ^л с _р v

( d ²

)

^{- к} T ⁵ 7 31

^а 1 A 1 A 3 exp ^[- i ( ^k 1 z ^{- k} 3 z ) ^z ]

+------------------------------- = 0.

^л c p ^v

При записи уравнений, описывающих изменение пространственного спектра объектной

волны по толщине нелинейного слоя, спектра температурной решетки 5 T 31 , считали, что к 6 = к 2 + к т + к 1 т , к т = К 1 - к 3 .

При выполнении граничных условий A 1 ( z = 0) = ^                 ^

= A 10 , A 2 ^{( z} = ^ ) = A 20 , A 3 ^(к 3 , ^z = ⁰⁾ = A 30 ^(к 3 ) ^решение первых трех уравнений системы (3) есть

A 1 ( z ) = A 10 exp [ - С 1 ( z ) ] ,

A 2 ( z ) = A 20 exp [ - С 2 ( / ) + С 2 ( z ) ] ,                  (5)

A 3 ^(к 3 , ^z ) = ^A 30 ( ^к 3 ) exp [ ^{- С} 1 ^{( z} ) ] .

Здесь

С 1,2 ( z ) = J j i 0 I

^k 1,2   dn

^{5 T} 0 ^{( z} 1 ) ^{+ n} 1,20 [ ^dT

⁺¹ dn ^{(5 т} ( d

С учетом (5) при выполнении граничного условия A 6 ( к 6 , z = I ) = 0 из (3) выражение для про-

При условии, что температура на гранях нелинейного слоя не меняется 5 7 31 ( к т , z = 0 ) = = 5 7 31 ( к т , z = £ ) = 0, решение уравнения (7) есть f

5 ^т31(к т,z) = 2   ^2- x р - к т

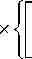
T

- { exp(-к tz ) [ exp(к т £ ) - exp(-P £ ) ] } +

^{£                                              (8)}

+--

2 sh к т

- exp(-P z ) ] } .

Здесь f = [« 1 Л ю AA з 0 (к 3 )]/(Л C p v), к т = |к т\ , в = = 2« 1 + i ( k 1 z - k 3 z ).

Выражение (6) с учетом (8) устанавливает однозначную связь между пространственными спектрами объектной и сигнальной волн. Из (6), (8) следует, что с учетом рассматриваемых приближений пространственная селективность шестиволнового преобразователя излучения, как и четырехволнового преобразователя [11], не зависит от тепловых параметров нелинейной среды (Л, C p ), а определяется только толщиной среды, частотами взаимодействующих волн и коэффициентом поглощения.

- { exp(к tz ) [ exp(-p Z ) - exp(-к т £ ) ] } -

2. Обсуждение результатов

Из требования, чтобы волна с удвоенным обращенным фронтом распространялась навстречу сигнальной волне, вытекает условие на частоты взаимодействующих волн вида

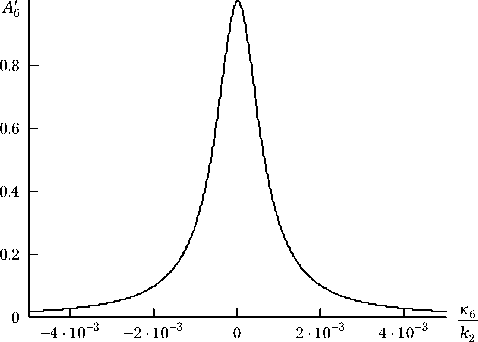
Рис. 2. Зависимость модуля спектра объектной волны от пространственной частоты при а^ = 1, 2 к 1 ^ = 10⁴, к/к 1 = 0.5

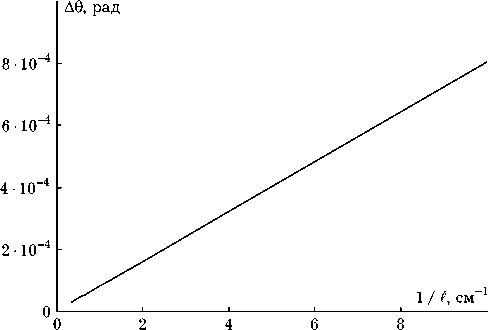
Рис. 3. Зависимость полуширины углового спектра объектной волны от обратной толщины нелинейного слоя при а 1 = 1 см ^{- 1}, к 1 = 7.85 ■ 10⁴ см^-1, к 2 = 2 к 1

^{2 n} 10 ® 1 = n 20 ® 2 • (9) Невыполнение условия (9) приводит к угловому повороту объектной волны по отношению к сигнальной волне.

Будем рассматривать случай, когда волны накачки распространяются строго вдоль оси Z , т. е. K 1 = к 2 = 0. На рис. 2 в параксиальном приближении ( k 1 z - к зz = к 3 / 2 k 1 , к 2_z - к б_z = = -к 6 / 2 k 2 ) для сигнальной волны от точечного источника, расположенного на передней грани нелинейного слоя ( A 3о (к 3 ) = 1), приведен характерный график нормированного на максимальное значение пространственного спектра объектной волны ( A 6 = A 6 ( к 6 , z = 0 )/ A 6max| , A 6max = A 6 ( к 6 = 0, z = 0 ) — наибольшее значение модуля пространственного спектра). Видно, что с увеличением пространственной частоты ( к б = |к 61) модуль пространственного спектра объектной волны уменьшается.

Угловой поворот второй волны накачки ( к 2 * 0 ) приводит к смещению положения максимума пространственного спектра объектной волны на величину поворота, при этом вид зависимости модуля пространственного спектра объектной волны от пространственной частоты не меняется.

Для характеристики качества удвоенного обращения волнового фронта шестиволновым преобразователем излучения введем полуширину полосы пространственных частот ( Ак ) , определяемую из уравнения

A 6 ( ^к 6 =^Ак, z = 0 ) = ¹ A 6max .

Для сигнальной волны с гауссовым пространственным спектром (Aз0(к3) = ехр[-к3 / кз0]) увеличение ее расходимости (кз0 ^ м) приводит к росту полуширины полосы пространственных частот объектной волны с последующим выходом на постоянное значение, которое равно значению полуширины полосы пространственных частот в случае сигнальной волны от точечного источника.

Увеличение толщины нелинейного слоя в области I < 2/а 1 , которая, как правило, реализуется в экспериментах по многоволновому взаимодействию в поглощающих средах, приводит к сужению полуширины углового спектра (А0 = Ак / к 2 ) объектной волны (рис. 3). Характер изменения полуширины углового спектра от толщины нелинейного слоя хорошо описывается зависимостью вида

А0 = в .

/

Здесь в — коэффициент, обратно пропорциональный частоте второй волны накачки.

Из выражения для пространственного спектра объектной волны (6) с учетом (8) следует, что изменение фазы объектной волны ( Аф ) на полуширине ее углового спектра незначительно: Аф < 10 ^{- 2} рад.

Анализ значений ширины углового спектра объектной волны показывает, что множитель exp [- i ( к 2z - к 4 z ) z ] в выражении (6) слабо влияет на пространственный спектр объектной волны. Пространственный спектр волны c удвоенным обращенным волновым фронтом определяется интегралом по толщине нелинейного слоя функций корреляций пространственных спектров температурных решеток . Это объясняет линейную зависимость ширины углового спектра объектной волны от обратного значения частоты второй волны накачки.

Приведем оценки полуширины углового спектра объектной волны. В качестве среды с тепловой нелинейностью возьмем этанольный раствор хлорида меди с коэффициентом поглощения a i = 2 мм 1 , толщиной £ = 0.5 мм [7]. Пусть длина волны первой волны накачки и сигнальной волны λ₁ = 1064 нм, длина волны второй волны накачки λ₂ =532 нм. Тогда полуширина углового спектра объектной волны будет равна ∆θ = 7,4 ⋅ 10 ^{- 4} рад.

Заключение