Удвоенное обращение волнового фронта при шестиволновом взаимодействии на керровской нелинейности в волноводе с бесконечно проводящими поверхностями

Наличие в среде нелинейной восприимчивости пятого порядка позволяет при реализации шестиволнового взаимодействия вида ω ₁ +ω ₁ -ω ₁ --ω ₁ +ω ₂ =ω ₂ получить волну, комплексная амплитуда которой пропорциональна квадрату комплексно сопряженной амплитуды сигнальной волны (волны с удвоенным обращенным волновым фронтом (УОВФ)) [1–2]. Генерация волны с УОВФ расширяет возможности использования шестиволновых преобразователей излучения в задачах коррекции фазовых искажений, преобразования сложных пространственно неоднородных волн и т. д. [3].

С целью увеличения эффективности многоволновых преобразователей целесообразно от рассмотрения взаимодействия в неограниченных по поперечным размерам средах перейти к исследованию взаимодействия в волноводах [4–6]. При этом, когда речь идет о преобразовании сложных пространственно неоднородных полей, всегда встает вопрос о качестве преобразования, то есть о соответствии комплексных амплитуд сигнальной волны и волны с удвоенным обращенным волновым фронтом [7–8].

В настоящей работе анализируется влияние на качество УОВФ при шестиволновом взаимодействии в волноводе с бесконечно проводящими поверхностями, заполненном средой с керровской нелинейностью, пространственной структуры волн накачки при условии, что отношение волновых чисел волн накачки кратно целому или полуцелому числам.

• 1.    Основная часть

Пусть в волноводе, расположенном между плоскостями, навстречу друг другу распространяются две волны накачки с комплексными амплитудами A i и A 2 , частотами ® 1 и ® 2 , сигнальная волна с комплексной амплитудой A ₃ на частоте ® 1 . В среде наводится нелинейная поляризация ( A i A 3 ) ² A 2 , являющая источником объектной волны с комплексной амплитудой A 6 на частоте ® 2 . Фаза объектной волны пропорциональна взятой со знаком минус удвоенной фазе сигнальной волны (волны с удвоенным обращенным волновым фронтом).

В приближении заданного поля по волнам накачки при малом коэффициенте преобразования без учета изменения показателя преломления из за самовоздействия волн накачки амплитуда объектной волны с УОВФ на передней грани волновода есть [9]:

N ₂

A 6 ( x ^, z = 0) = ^ a 6 r f r ( x ^, (% ) = r = 0

N ₂

i~ У

2 ^

^

f r ⁽ x ^{, (} 2 )

P r

N ₁ N ₁ N ₂ N ₁ N ₁ szsxz p = 0 p '= 0 m = 0 s = 0 s '= 0

a ⁽ 0Ц 0 ) a l p ^a ip'

( 0 ) ( 0 ) * ( 0 ) *

x ^; у >    , sin

2 m 3 s   3 s ' ^Y pp mss r

^А pp mss r ¹

2 к          7

x exp

—

pp mss r

Заметим, что если при четырехволновом взаимодействии знание ФРТ полностью описывает точность ОВФ, то нелинейный характер связи между комплексной амплитудой объектной волны и комплексной амплитудой сигнальной волны позволяет с использованием ФРТ говорить лишь качественно о точности УОВФ.

В качестве волновода рассмотрим двумерный волновод с бесконечно проводящими поверхностями, расположенными на расстоянии 2 a друг от друга, он заполнен средой с показателем преломления n 1 . Модами такого волновода являются функции [12]:

^{30 n} ®2 (5) (5)

Здесь g =----— x Г X ' - нелинейная восприим- c2

чивость пятого порядка; a^, a 30’ - коэффициенты в разложении амплитуд первой волны накачки, сигнальной волны на передней грани по модам волновода; a — m - коэффициенты в разложении амплитуды второй волны накачки на задней грани по модам волновода; f r ( x, о^ — ) и в r ( о^ ) - поперечная составляющая и постоянная распространения r -й моды волновода; N ₁ и N ₂ – число мод волновода на частотах 0) 1 и о — , учитываемых при расчете амплитуды волны с УОВФ;

f r ( ^x ) = “Г ^sin a

п ( r + 1)

------^J- ( x + a ) •

2 a

Для приосевых мод волновода постоянная распространения r -й моды есть

P r ^(о 1,2 ) ~ ^k 1,2 ^— 2 k

п ( r + 1 )

2 a

,

^А pp'mss'r = ^в p ^{+ в} p ' ^{— в} m — ^в s* — ^в s '* ^{+ в} r

– волновая расстройка;

Y pp' mss' r = f f p ( ^x , ⁽ 1 ) f p ' ( ^x , ⁽ 1 ) ^f m ( ^x , ⁽ 2 ) ^{x x} f s ( ^{x , (} 1 ) f s ' ( ^{x , (} 1 ) f r ( ^{x , (} 2 ) ^dx

( 1,2

где k 12 = ——n 1 ( ^ 12 ) - волновое число. ^, c ^,

Условие шестиволнового взаимодействия с УОВФ в длинном волноводе с бесконечно проводящими поверхностями запишется следующим образом:

h ( p + 1 ) ² + ( p ' + 1 ) ² — ( s + 1 ) ² — ( s ' + 1 ) ² —             (5)

( m + 1 ) ² — ( r + 1 ) ² = 0.

– интеграл перекрытия.

Для сигнальной волны от точечного источника

(A з ( x , z = 0) = 5 ( x — x 0 ), x 0 - координата, определя-

ющая смещение точечного источника относительно оси волновода) в случае длинных волноводов, то есть считаем выполняется условие Re( А      ) / »

pp mss r

» 1, если Re( А pp,mss,r ) ^ 0, выражение для амплитуды объектной волны примет вид

gt N — fr ( x , 0 2 )

^{G ( x , x} 0 ^, z = 0 ) = ^— i ^ ^—---- ^{x 2} r = 0     ^в r

N ₁ N ₁ N ₂ N ₁

хУУУУа(0 )a( 0 )a( 0) f   to x ^ ^ ^.^ alp alp' a2mfs(x0, (1)x p=0 p '=0 m=0 s=0

Здесь h = k 2 I k 1 .

В случае когда отношение волновых чисел волн накачки не равно целому или отношению целых чисел, условие (5) выполняется, только когда номер моды объектной волны совпадает с номером моды второй волны накачки ( r = m ). Это уменьшает количество комбинаций мод волновода, участвующих в формировании волны с УОВФ.

На рис. 1 приведены характерные нормированные графики зависимости модулей функций размытия точки, расположенной на оси волново-

^{x f}_s' ^{( x} 0 , ⁽ 1 h ppmssr •

r^r да ( G =	G ( x , x 0 = 0, z = 0 )	, G max - максимальное
	G max

Как и в случае рассмотрения качества обращения волнового фронта при четырехволновом взаимодействии [10-11], функцию G ( x , x 0 , z = 0) будем называть функцией размытия точки (ФРТ).

значение функции), от нормированной поперечной координаты при условии, что первая вол на накачки одномодовая с номером моды p = 0, а амплитуда второй волны накачки на задней грани волновода описывается гауссовой функцией

а

б

в                                                                   г

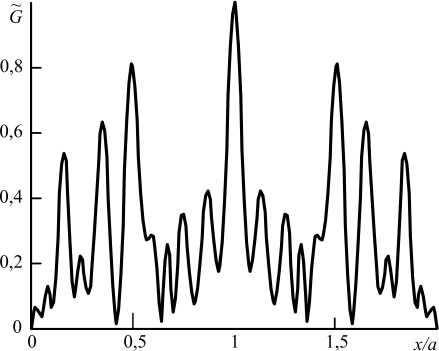
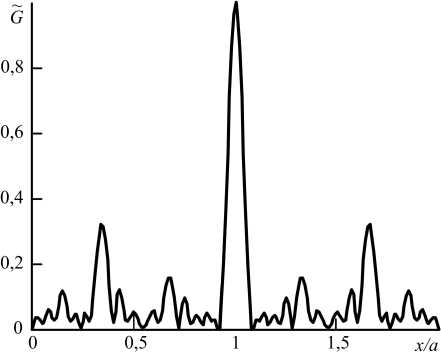
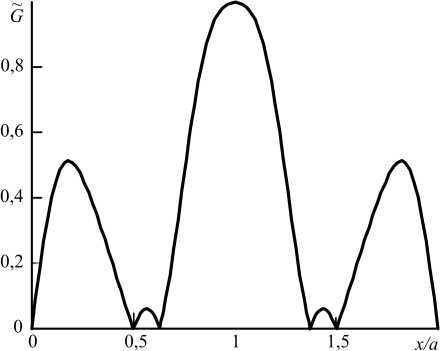
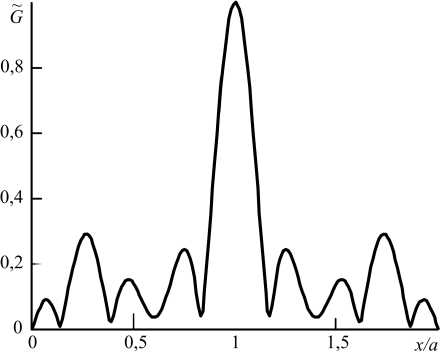
Рис. 1. Зависимость модуля ФРТ от поперечной координаты при h = 2 ( а , б) , 0,5 ( в , г ): первая волна накачки одномодовая с номером моды p = 0, амплитуда второй волны накачки меняется по гауссову закону, a/b = 1 ( а , в ), 8 ( б , г )

Fig. 1. Dependence of the PSF modulus on the transverse coordinate at h = 2 ( a , b ), 0,5 ( c , d ): the first pump wave is single-mode with the mode number p = 0, the amplitude of the second pump wave changes according to the Gaussian law, alb = 1 ( a , c ), 8 ( b , d )

A 2 ( x , z = I ) = exp( - x ² / b ² ). Здесь b - ширина волны накачки.

Аналогичные графики зависимости модулей функций размытия точки наблюдаются, когда одномодовой с номером моды m = 0 является вторая волна накачки, а амплитуда первой волны накачки на передней грани волновода описывается гауссовой функцией A 1 ( x , z = 0) = exp( - x ² / b ² ).

При расчете модуля ФРТ учитывали 20 мод сигнальной волны, первой волны накачки, и 20h мод объектной волны, второй волны накачки.

Как при учете гауссовой структуры первой волны накачки, так и при учете гауссовой структуры второй волны накачки модуль ФРТ состоит из центрального и боковых максимумов. При фиксированной частоте первой волны накачки увеличение частоты второй волны накачки повышает число побочных максимумов, уменьшает ширину центрального максимума. Изменение ширины га- уссовой волны накачки меняет соотношение между центральным и боковыми максимумами, влияет на ширину центрального максимума.

В качестве количественных параметров, характеризующих качество УОВФ, могут выступать полуширина центрального максимума модуля ФРТ ( Д x ), определяемая из решения уравнения

| G (x = Дx, x 0 = 0, z = 0 )|= (6) =1G (x = a,x 0 = 0,z = 0 )|, и контраст модуля ФРТ, определяемый как отношение значения центрального максимума к наибольшему значению одного из побочных максимумов (K).

Очевидно, что использование для анализа качества УОВФ полуширины центрального максимума модуля ФРТ предполагает наличие ярко выраженного центрального максимума. В противном случае, который наблюдается, например,

а

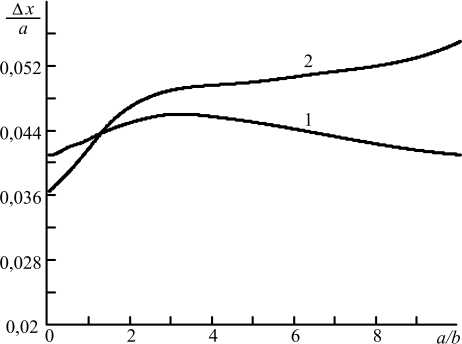
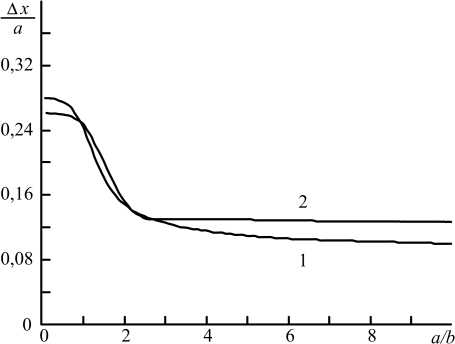
Рис. 2. Зависимость полуширины центрального максимума модуля ФРТ от ширины гауссовой волны накачки: вторая волна накачки гауссова, первая волна накачки одномодовая (1); первая волна накачки гауссова, вторая волна накачки одномодовая (2) при h = 2 ( а ), 0,5 ( б)

Fig. 2. Dependence of the half-width of the central maximum of the PSF module on the width of the Gaussian pump wave: the second pump wave is Gaussian, the first pump wave is single-mode (1); the first pump wave is Gaussian, the second pump wave is single-mode (2) at h = 2 ( a ), 0,5 ( b )

б

а

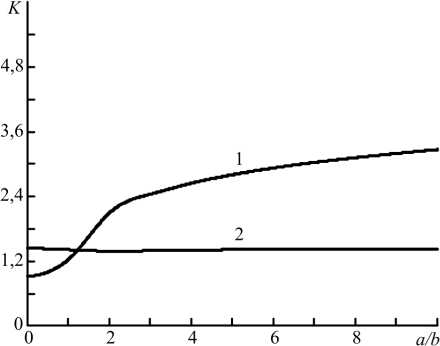
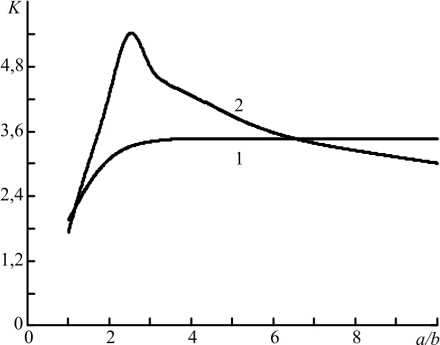
Рис. 3. Зависимость контраста модуля ФРТ от ширины гауссовой волны накачки: вторая волна накачки гауссова, первая волна накачки одномодовая (1); первая волна накачки гауссова, вторая волна накачки одномодовая (2) при h = 2 ( а ), 0,5 ( б )

Fig. 3. Dependence of the contrast of the PSF module on the width of the Gaussian pump wave: the second pump wave is Gaussian, the first pump wave is single-mode (1); the first pump wave is Gaussian, the second pump wave is single-mode (2) at h = 2 ( a ), 0,5 ( b )

б

при h = 0,5 и b > a , использовать этот параметр для анализа качества УОВФ не представляется возможным.

Улучшение качества УОВФ предполагает как сужение центрального максимума, так и увеличение контраста модуля ФРТ.

В случае h = 2 при уменьшении ширины второй гауссовой волны накачки при условии одномодовой первой волны накачки c номером моды p = 0 полуширина центрального максимума модуля ФРТ меняется слабо и монотонно увеличивается при уменьшении полуширины первой гауссовой волны накачки при условии одномодовой второй волны накачки c номером моды m = 0 (рис. 2, а). В диапазоне изменения ширины второй гауссовой волны накачки от b = 0,125а до b = 1,25а полуширина центрального максимума модуля ФРТ меняется от 0,043а до 0,047а, а при изменении в этом диапазоне ширины первой волны накачки увеличивается от 0,041а до 0,052а.

Контраст модуля ФРТ с уменьшением ширины второй гауссовой волны накачки при условии одномодовой первой волны накачки возрастает и слабо меняется с изменением ширины первой гауссовой волны накачки при условии одномодовой второй волны накачки (рис. 3, а ).

В случае h = 0,5 при уменьшении ширины либо первой, либо второй гауссовых волн накачки полуширина центрального максимума модуля ФРТ уменьшается (рис. 2, б). В диапазоне изменения b от 0,125a до 1,25a полуширина центрального максимума модуля ФРТ уменьшается от 0,26а до 0,13а при условии, что амплитуда первой волны накачки меняется по гауссову закону, от 0,26а до 0,10а - при условии, что амплитуда второй волны накачки меняется по гауссову закону

Контраст модуля ФРТ в диапазоне изменения b от 0,125 а до 1,25 а при уменьшении ширины второй гауссовой волны накачки, увеличиваясь, выходит на постоянное значение, равное 3,46. При уменьшении ширины первой гауссовой волны накачки контраст модуля ФРТ вначале увеличивается, достигает максимального значения, равного 5,41, а затем медленно уменьшается (рис. 3, б ).

Максимальное значение скорости изменения контраста, полуширины центрального максимума модуля ФРТ как для h = 2, так и для h = 0,5 наблюдается в диапазоне изменения ширины гауссовых волн накачки от b = 0,3 а до b = 2 а . При дальнейшем уменьшении ширины гауссовой волны накачки скорости изменения как полуширины центрального максимума, так и контраста модуля ФРТ значительно снижаются и в ряде случаев стремятся к нулю. Таким образом, основное влияние ширины гауссовой волны накачки на качество УОВФ наблюдается в диапазоне ширин волн накачки от b = 0,3 а до b = 2 а.

Заключение

При отношении волновых чисел второй и первой волн накачки, равном 2 и 0,5, проанализировано качество удвоенного обращения волнового фронта сигнальной волны от точечного источника при шестиволновом взаимодействии на керровской нелинейности в волноводе с бесконечно проводящими стенками.

Показано, что максимальное изменение характеристик волны с УОВФ наблюдается при изменении ширины гауссовых волн накачки от b = 0,3 а до b = 2 а. В этом диапазоне при h = 0,5 уменьшение ширины гауссовых волн накачки приводит как к сокращению полуширины центрального максимума, так и к увеличению контраста модуля ФРТ. При h = 2 уменьшение ширины первой гауссовой волны накачки при условии одномодовой второй волны накачки увеличивает полуширину центрального максимума и слабо влияет на контраст модуля ФРТ. Качество удвоенного обращения волнового фронта сигнальной волны от точечного источника, расположенного на передней грани волновода, с уменьшением ширины первой гауссовой волны накачки ухудшается.