Ultrasound Image Despeckling using Local Binary Pattern Weighted Linear Filtering

Published Online May 2013 in MECS

Ultrasound machine uses high frequency sound waves to capture pictures. The coherent nature of ultrasound imaging, results in the formation of a multiplicative noise called speckle noise. Speckle noise appears as a granular pattern which varies depending upon the type of biological tissue. The interference of backscattered signals result in speckle noise and its apparent resolution is beyond the functionalities of the imaging system. Noise content is usually stronger than the microstructure of tissue parenchyma and reduces the visibility and masks the tissue under investigation. Therefore the main challenge in despeckling is to filter the noise content without affecting the microstructures and edges.

Despeckling can be done in two ways. It can apply directly on phase of RF signal [2] and it can also be used as post processing techniques applied on images. Different methods like linear and non linear filtering, wavelet based despeckling etc. have been proposed to reduce the noise. Chinrungrueng et al. propose edge preserving noise reduction method using two dimensional Savitsky Golay filters which is based on the least square fitting of a polynomial function to image intensities [3],[4]. Though it takes less computation time than median filter the effect of noise reduction was same as that of median filter. A modified hybrid median filter and adaptive weighted median filter have been reported in the literature [5],[6]. Sivakumar et al. proposes an improved mean filter using fuzzy similarity [7]. A cumulative speckle reduction algorithm for spatial and diffusion filter and the modified anisotropic diffusion based on partial differential equation has been developed [8], [9]. Filtering using wavelet transformation, multi scale wavelet domain transformation, wavelet shrinkage, wavelet thresholding anisotropic diffusion etc. can be found in various studies [10]-[16]. Another method based on Ricardo reduces the split spectrum processing that occurs as a result of one dimensional narrow band filters [17]. Yang et al. [18] proposes an edge preserving denoising method based on bilateral filter and Gaussian scale mixtures in shiftable complex directional pyramid domain. Bhadauria et.al proposes an adaptive fusion of curvelet transform and total variation for denoising medical images [19].

The proposed system is tested with ultrasound placenta images and kidney images. Ultrasound placenta images of different grades are shown in Figure 1. Ultrasound is the best ideal tool to determine the fetal growth and position [20]. Noise suppression is very important to arrive at correct decision and to overcome the variability in diagnosis. Human interpretation and diagnosis becomes easy and accurate. The novelty of the proposed work is the introduction of local binary patterns to noise reduction process. No despeckling algorithm has been reported in the literature using the LBP approach.

The rest of the paper is organized as follows. Section 2 describes the speckle noise in ultrasound images and different noise reduction algorithms that are considered in this study. The proposed algorithm is also given. In section 3 result analysis using ultrasound images and discussion are presented. Conclusion and future work are given in the final section.

called speckle noise [21]. Multiple examination of the same object under different machine condition forms identical speckle patterns. Speckle patterns generally changes with the change in machine condition. There exists no relation between the speckle and texture pattern which depicts the actual histological structure of object. The output of ultrasound signal can be modeled as,

g ( x, У ) = f ( x, У ) n ( x, У ) + n ( x, У )

Where

g(x, y)

noise free pixel,

is the noisy pixel,

f(x,y)is the

^{n (} x , у ) and П ^(x , У ) represents the

multiplicative and additive noise respectively, x and y are the indices of the spatial locations which belong to the 2D space of real numbers. The effect of additive noise is less than that of multiplicative noise, therefore the above equation after logarithmic compression we can write as the sum of noise free pixel and noise

component.

g (x, У ) = f (x, У) + n (x, У )

Better image quality helps in easy and accurate diagnostic decision making. The widespread use of ultrasound imaging necessitates the need for developing despeckling filters for reducing noise. The performance of the proposed filter is compared with some of the existing filters such as mean filter, median filter, diffusion filter and wiener filter.

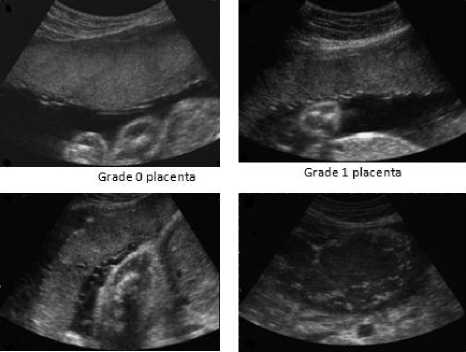
Grade 2 placenta                  Grade 3 placenta

Fig. 1: Sample images of ultrasound placenta in different grades

2.1 Mean Filter

Conventional mean filter replaces the value of every pixel in the image by the mean of the intensity level defined over a neighborhood. As a result sharp transitions in intensity get reduced. Mean filters fail to preserve edges and small details in an image. The basic linear filtering operation can be re presented as,

f (x, У ) = g ^ + w( x, У)(g (x, У ) - g ~ )

Where g is the local mean value of a region

surrounding and including the pixel

g(x, y)

,

w(x, y)

is the weight with values in the range [0, 1].

The image obtained will be blurred.

• 2.2 Wiener Filter

Wiener filter is more data driven and relies on the homogeneous appearance of the image. It is developed based on the assumption that the image properties and the characteristics of noise are same over different regions. This is not true in practical situation. Therefore adaptive wiener filtering has been developed. Wiener filter also uses local statistics in a moving window. The

y ) in equation 3 becomes

term

w(x,y)=(σ2-σ2n)/σ2

.

2 _σ ²

Where σ and ⁿ represent the variance in the moving window and the variance of noise in the image. In frequency domain wiener filter tends to weaken low energy components which give more information regarding image detail. In the power spectrum, the noise and image content show similar properties ^[22].

2.3 Diffusion Filter

Perona and Malik [23] proposed a PDE (Partial differential Equation) based speckle noise reduction method using the concept of scale space. In scale space representation the original image is embedded into a family of more simpler and global representation where semantic information can be extracted easily. They tried to reduce the diffusivity of edge like locations in which a transition in intensity level occurs. The diffusion coefficient is adjusted to give more priority to intraregional smoothing than interregional smoothing. Perona Malik diffusion is based on the flowing equation.

∂ u = div(g(I∇u 2)∇u

The diffusivity

g(s2)=

11+ s2/λ2

(λ >- 0)

The disadvantage of diffusion filtering is the correspondence problem which occurs mainly due to the dislocation of edge from finer to coarser region. Also there exists the chance of losing some relevant information while smoothing.

• 2.4    Median Filter

• 2.5    Proposed Local Binary Pattern Linear Filter

Median filter is a non linear order static filter that replaces the middle pixel in the neighborhood window with the median value [7]. Generally an odd number is chosen as the size of the neighborhood so that a well defined center value exists. If the neighborhood region of a median filter contains an edge, it preserves the edge under the following conditions: the edge is straight within the neighborhood region, the signal difference of the two regions incident to the edge exceeds the noise amplitude and the signal is locally constant within each of the two regions [24]. Its performance is poor when the number of noise pixels is greater than or equal to half the number of pixels in the neighborhood.

LBP is a gray scale invariant that describes local primitives such as curved edges, points, spot, flat areas etc.[25]. LBP methodology has contributed a vital role in texture analysis. It is widely used in different computer vision problems such as face recognition, motion analysis, medical image analysis, finger print recognition, palm print recognition, vessel extraction of conjunctiva images etc.[26]-[31]. Over the past ten years different variant to LBP such as uniform patterns, dominant local binary pattern, combination of Gabor and LBP, center symmetric local binary pattern etc. has been reported in the literature [32]-[35]. To generate LBP code for a neighborhood, the weight assigned to each pixel is multiplied with a numerical threshold. The process is repeated for a set of circular samples. Figure 2 shows the process of LBP code generation for a circular neighborhood.

Circular neighborhood

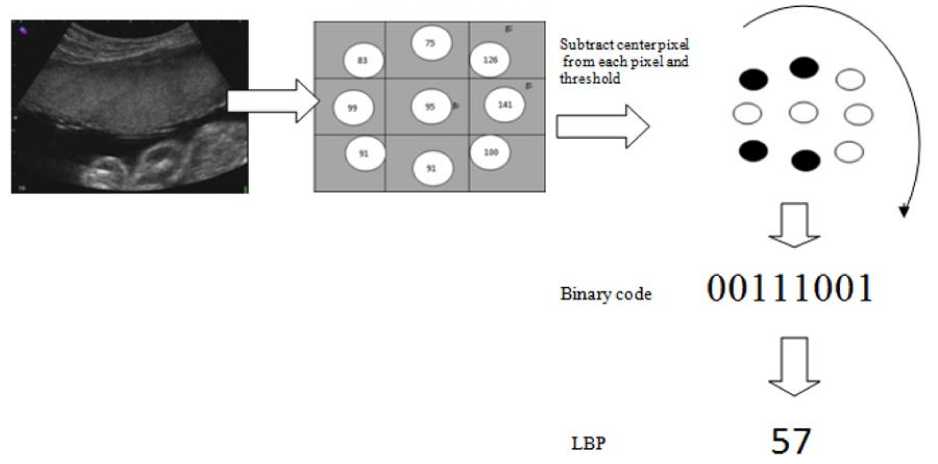
Fig. 2: Sample images of ultrasound placenta in different grades

Texture over a neighborhood of pixels can be defined as the joint distribution of the gray value of a central pixel of the neighborhood say g c and gray value of circular pixels located at distance P.

T = t(gc, g 0, g 1,.... gp-1)

The local texture pattern of a neighborhood can be obtained from the difference of central pixels and each pixel in the neighborhood. As the differences are independent this joint distribution can be factorized:

T * t ( gc ) t(g 0 - gc,-, gp-1 - gc )

ranging from 3.5 to 5 MHz. Machine settings were optimized to ensure that, the images taken are good in quality. The examinations were conducted transabdominally by an experienced radiologist. The despeckling process is carried out on a personal computer with Intel core 2 Duo processor of 2.93 GHz speed with 4.00 GB RAM. The algorithm is implemented using Matlab 7 with Windows 7 as operating system. Initially, the well known median filtering has been applied to make the ultrasound image noise free. To the noise free image, speckle noise of zero mean and variance 0.2 are added. Then the original image is reconstructed using despeckling filters. Figure 3 shows the example of a noisy image.

To make this invariant against all transformations the signs of the difference are also considered and the

overall luminance

t(gc)

contribute anything to texture analysis.

is ignored as it does not

T * t(s(g0 - gc X — s(gp-1 - gc))

s ( x ) =

Г 1 X >  0

0 x < 0

By assigning weight, this difference is converted to a Local Binary Pattern Code which is equivalent to the local texture. The following expression will generate 2p LBP values for a neighborhood of pixels located at distance p.

p - 1

LBPp,R (xc, yc) = Z s(gp - gc )2p p=0                             (9)

g

Where ^c is the gray value of a central pixel of the neighborhood. The process is repeated for a set of circular samples. The histogram of the LBP codes is widely used as texture descriptor. To reduce the size of the descriptors only uniform patterns- binary patterns that occurs more frequently than others are considered. These values are normalized and used for the filtering operation. The proposed approach uses the local binary patterns as the coefficient of filtering. The proposed method follows a weighted linear filtering approach. It replaces the conventional local statistics in weighted linear filtering with local binary pattern approach. This method uses LBP to calculate the weight in the linear filter of the form:

f(x, У) = g ^ + w( x, y)(g(x, y)- g ~ )

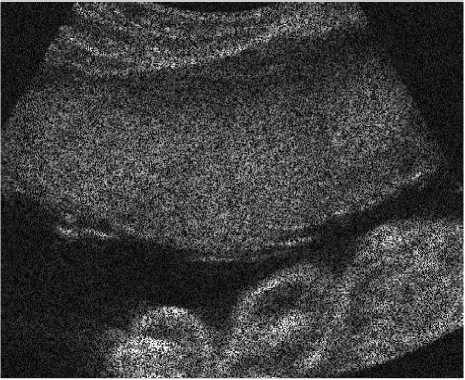
Fig. 3: ultrasound image corrupted with speckle noise

We compare the performance of the proposed method with some of the conventional approaches in speckle reduction: diffusion filtering, mean filtering and wiener filtering. The quantitative measurements used for performance evaluation are Mean Squared Error (MSE), Root Mean Squared Error (RMSE), Signal to noise Ratio (SNR), Peak Signal to noise Ratio (PSNR) and Structural Similarity Index (SSIN). The performance of the system is also evaluated using one of the best qualitative measurements - Universal Quality Index (UQI). It models any distortions in image as a combination of three factors such as loss of correlation, luminance distortion and contrast distortion.

following equations are used for computing measures.

1 MN

MSE =    ZS (g (x, У) - f (x, У ))2

mn t! 7=1

III. Results and Discussion

The ultrasound imaging was carried out using Sonoline G50 ultrasound system with frequency

MN

RMSE = A ---SS(g(x, У)- f(x, У))2 MN^

The these

z z ( g ( x , y ) 2 - f ( x , y ) 2 )

^SNR = 10^ 10       •----------------------

ЕЁ ⁽ g ^{( x} , y ) ^{- f ( x} , y ⁾⁾²

MSE

PSNR = - 10log10 —--- g max

SSIN =

(2g"f  I c1)(2^gf + c2)

(g " + f" + c1)(CT

2 g + CT2 f + c 2),

-1 < SSIN < 1

UQI =

^ gf     ² f g

2стст fg

ст f CT _s ( f ~ ) ² + ( g ~ ) ² ст² f + ст² _g

Where

- 1 <  UQI <  1

g(x,y)is the

noisy pixel, f ( x , y )

is the

noise free pixel, g and

f

are the local mean value

of a region in the noise free and noisy image, ^{c 1} and c ² represents the dynamic range of ultrasound images ; ^{CT g CT} f represents the standard deviations of original despeckled values of the analysis window and gf represents the covariance between original and despeckled windows.

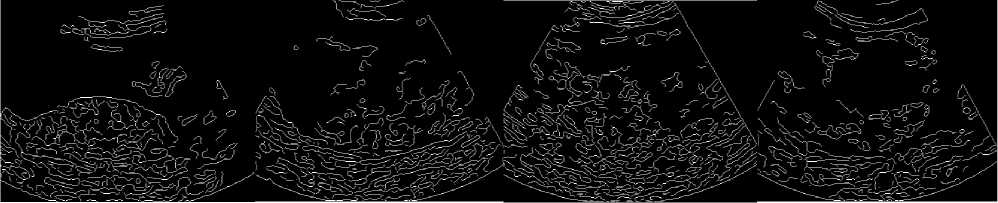
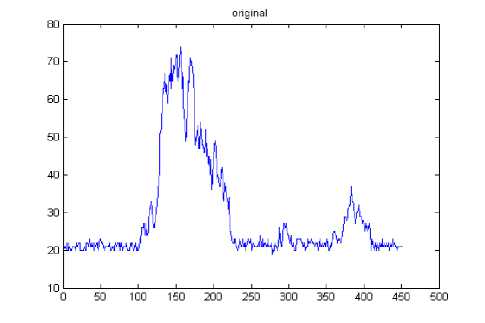
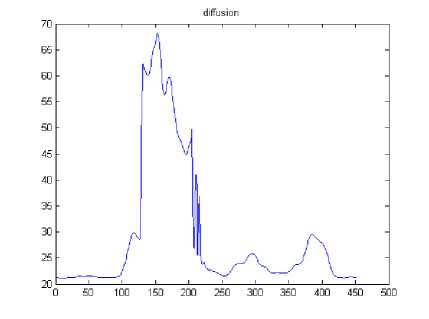
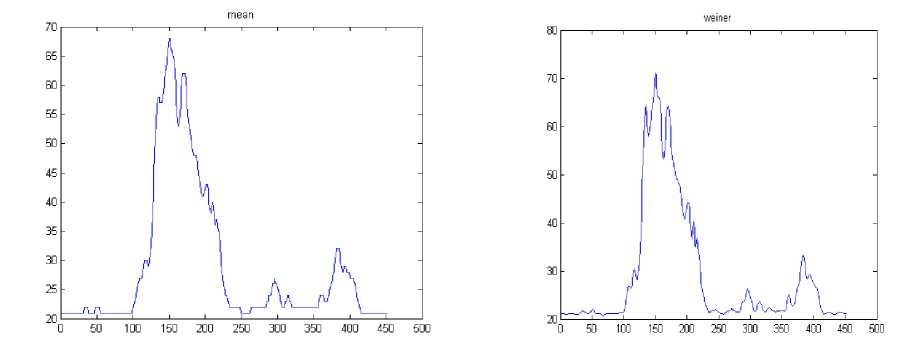
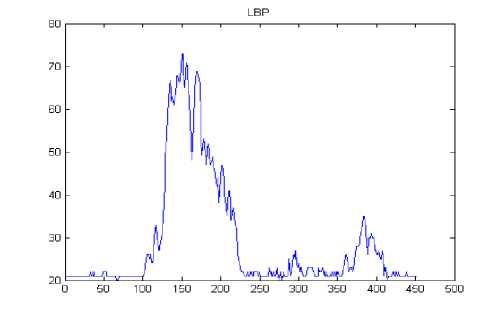
The results in Table 1 clearly demonstrate that the proposed method outperforms the other filters. The edge map of the proposed filter shows high similarity to edge map of original image than the other filters which indicate the superior performance of the proposed method in edge preservation. Figure 4 shows the horizontal intensity profile of a scan line passing through the centre of the original image and despeckled image using different filters such as diffusion, mean, wiener and proposed LBP filter. We can observe a close similarity between the intensity profile of the proposed LBP method and that of original image. The proposed method is also tested with ultrasound kidney images collected from ultrasound-images.com [36]. The quantitative results are shown in Table 2.

Table 1: MSE, RMSE, SNR, PSNR, SSIM, UQI values obtained for various filters

Grade 0 Placenta
	MSE	RMSE	SNR	PSNR	SSIM	UQI
diffusion filter	30.0673	5.4834	24.4235	35.1172	0.8126	0.4227
mean filter	30.2667	5.5015	24.3765	35.0885	0.8291	0.5468
wiener filter	19.7550	4.4447	26.2505	36.9414	0.8677	0.6335
proposed filter	11.1425	3.3380	28.7395	39.4283	0.9329	0.7991
Grade 1 Placenta
	MSE	RMSE	SNR	PSNR	SSIM	UQI
diffusion filter	23.4549	4.8430	4.8430	35.7524	0.8602	0.4019
mean filter	25.9858	5.0976	25.4537	35.3073	0.8736	0.5741
wiener filter	13.0994	3.6193	28.4503	38.2822	0.9167	0.6502
proposed filter	7.8416	2.8003	30.6802	40.5106	0.9561	0.7668
Grade 2 Placenta
	MSE	RMSE	SNR	PSNR	SSIM	UQI
diffusion filter	42.6805	6.5330	22.1915	32.5531	0.7860	0.4586
mean filter	63.3604	7.9599	20.4313	30.8372	0.7494	0.4717
wiener filter	36.9114	6.0755	22.8177	33.1838	0.8152	0.5792
proposed filter	19.1188	4.3725	25.6826	36.0408	0.9195	0.8236
Grade 3 Placenta
	MSE	RMSE	SNR	PSNR	SSIM	UQI
diffusion filter	20.3646	4.5127	22.8805	35.4047	0.8757	0.4078
mean filter	20.9073	4.5724	22.7414	35.2905	0.8895	0.5346
wiener filter	10.8094	3.2878	25.6424	38.1555	0.9266	0.6403
proposed filter	5.5919	2.3647	28.5127	41.0179	0.9671	0.8464

Table 2: MSE, RMSE, SNR, PSNR, SSIM, UQI values for various filters applied on ultrasound kidney images

	MSE	RMSE	SNR	PSNR	SSIM	UQI
diffusion filter	42.2944	6.5034	21.553	34.8783	0.8106	0.5223
mean filter	72.9593	8.5416	19.1161	32.5103	0.7715	0.6543
wiener filter	41.8041	6.4656	21.5932	34.9289	0.8283	0.7313
proposed filter	21.2596	4.6108	24.5443	37.8655	0.9351	0.8975

(a)                              (b)                              (c)                             (d)

(e)                              (f)                              (g)                             (h)

• (i)                                   (j)                                   (k)                                  (l)

  
  
  

(m)                          (n)                          (o)                          (p)

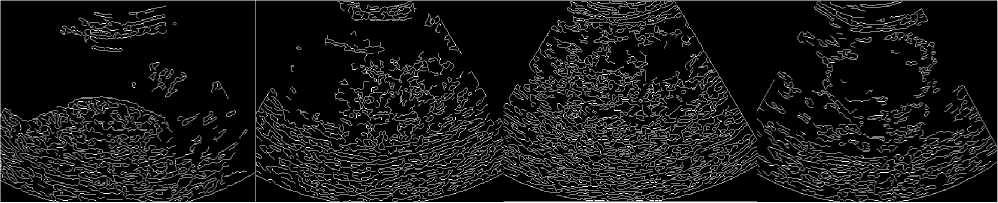
(q)                                (r)                                (s)                                (t)

Fig. 3: (a-d) dge map of noise free placenta images - grade 0 to grade 3, ( e-h) edge maps of despeckled placenta images using diffusion filter , (i-l) edge maps of despeckled placenta images using mean filter,

( m-p) edge maps of despeckled placenta images using wiener filter, (q-t) ) edge maps of despeckled placenta images using proposed LBP filter

(a)

(b)

(d)

(c)

(e)

Fig. 4: intensity profile of a scan line through the center of the image- grade 1.(a) original image, (b-e) despeckled image using diffusion filter, mean filter, wiener filter and proposed LBP filter.

• IV. Conclusion

In this paper, we have developed a liner filter for reducing the speckle noise in ultrasound images. The filter is based on uniform local binary patterns of the image. Compared to other filters the proposed filter produces better result by reducing noise without affecting the relevant information. The quantitative measures and edge preservation of the proposed LBP method is high. The proposed method is tested with ultrasound images of placenta and kidney which are of great clinical importance.