Улучшение нагрузочных характеристик радиальной опоры со сжимаемым смазочным слоем

Введение. В теории гидродинамической смазки эффект создания избыточного давления в тонком слое сжимаемой жидкости под действием вибрации называют обычно «вибронесущим» или эффектом «сдавливания слоя» и относят к разновидности гидродинамического эффекта [1, 2]. В теории вибронесущего слоя часто рассматриваются «медленные» течения смазки, которые обычно являются второстепенным процессом, связанным иногда с нежелательными явлениями, ухудшающими такие характеристики, как несущая способность, точность позиционирования подвеса и др. Однако процесс направленного течения смазки может быть существенно усилен и использован для создания ряда технических устройств компрессорного типа, дозаторов, газовых и жидкостных уплотнений и др. [3–5]. Этот же процесс можно использовать для нагнетания жидкой среды в смазочный слой, повышая тем самым ее количество и увеличивая смазочное действие подобно гидростатическим опорам [6]. Задача улучшения интегральных трибологических способностей смазочного слоя без увеличения массогабаритных и ухудшения других эксплута-ционных характеристик узла трения является актуальной.

В статье рассматривается направленное движение жидкости в зазоре с волнообразующими поверхностями с целью изучения нагнетательных свойств таких зазоров при наличии в них жидкости с различной величиной содержания газа. В качестве основного объекта исследования выбран цилиндрический сжимаемый слой, реализованный в зазоре со встречно направленными бегущими волнами колебаний, так как в этом случае можно отдельно изучить жесткостные и нагнeтaтeльныe характеристики такого типового «циклического» слоя, в котором увеличение давлений не всегда приводит к увеличению его несущей способности [2].

Показано, что для сжимаемых сред происходит увеличение давлений и массы в направлении движения бегущей волны, аналогично смазочным средам с несжимаемой жидкостной смазкой

[7, 8], но это увеличение с ростом частоты бегущей волны происходит не линейно, а имеет некоторый максимум, за которым наблюдается уменьшение эффекта нагнетания до уровней, присущих обычной вибронесущей опоре с равномерным сдавливанием слоя [2]. Если нагнетательные свойства слоев с бегущей волной уже достаточно изучены [6–8], то жесткость слоя и характеристики замкнутых подшипников на основе таких слоев смазки до сих пор не известны.

Математическая модель. В зазоре могут быть реализованы несколько разнонаправленных бегущих волн колебаний, производящих нагнетание среды или в центральную часть зазора, или к его периферии. Основным объектом исследования, как указывалось выше, является типовой узел – тонкий цилиндрический слой сжимаемый жидкости, ограниченный деформируемыми поверхностями, на одной из поверхностей которых реализованы две встречно направленные симметричные бегущие волны колебаний (рис. 1).

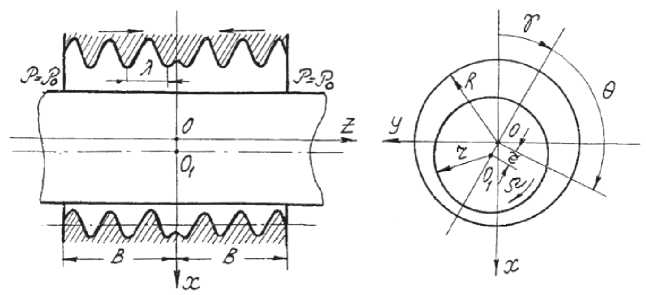
Рис. 1. Схема зазора с волнообразующими поверхностями

Безразмерную функцию зазора c бегущей волной запишем следующим образом: h

H =   = 1 + ecos6 + E0cos2n(T + r), в которой приняты обозначения: e = e / ho - безразмерный эксцентриситет; r = z / X - осевая ко ордината, отнесенная к длине бегущей волны X; в = B / X - безразмерная длина слоя; 6 - угловая координата; E0 = E / h0 - безразмерная амплитуда бегущей волны, h0 - номинальный зазор, т = tot.

В работе состояние сжимаемой среды описывается универсальными зависимостями следующего вида: плотность среды р = р ₁ + а ₁ ( р ₀ - p i ), где р ₀ и р ₁ - плотности газа и жидкости; вязкость среды ц = ц ₁ + а ₂ ( ц ₀ - ц ₁) , где ц ₀ и ц ₁ - вязкости газа и жидкости; зависимость между плотностью и давлением р = kP “ 3 , где а ₁, а ₂, а ₃ - параметры газосодержания, близкие друг другу ( ~а ) и определяемые в каждом конкретном случае по данным идентификационного эксперимента.

Ламинарное течение среды в зазоре при вращении одной из ограничивающих слой цилиндрических поверхностей с угловой скоростью Ω опишем с помощью усеченных уравнений Навье-Стокса [2], приведенных к виду уравнения для распределения давлений (Рейнольдса), в котором учтем параметр газосодержания α и соответствующие выбранной конфигурации слоя значения параметров Ламе:

л 5Т^а = ^{Л у} л , 5т

5 г 5 2а-1 H а 5Т1+а 2а-1 ^ 1 Т1+а5H а 1 5 г 5 2а-1 H а 5Т1+а 2а-1 ^ 1 Т1+а5H а 1 -ЛТа J 5 r 1 + а V 5 r 2а -1        5 r 2 56 1+а V 56 2а-1       56 / = где Лю = 12ц®R2 /(Poh02) и Л = 6цU0R/(Poh02) - безразмерные параметры «сдавливания» и «сжимаемости», в которых Uo = RQ - характерная относительная линейная скорость вращения ограничивающих слой поверхностей. Краевые условия для функции давлений Т можно получить на одном конце слоя как условие свободного края, а в геометрическом центре сопряжения в силу

Расчет и конструирование полной симметрии должно наблюдаться равенство нулю местного расхода среды в осевом на- правлении:

-     H i ( r = 0 , 0 , t) ,

f 2 a- 1                             2 a- 1 1

H . дТ ^{1 +}“     1      a д H ”

T

1 + a д r    2a -1        д r

= 0.

V r = 0

Для рассматриваемой конфигурации справедливо условие периодичности по угловой коор- динате:

T(r, 0 + 2n, t) = T (r, 0, t) .

В качестве начального условия принято

T ( r , 0 , t = 0 ) = 1 + e cos 0.

Для установившегося во времени процесса течения справедливо также условие периодично- сти во времени

T( r, 0, t + 1) = T( r, 0, t) .

Полученная смешанная краевая задача является нелинейной, что характерно для задач тонкого слоя со сжимаемой средой. Наиболее часто используемый метод решения – это метод малого параметра, в качестве которого обычно принимаются малые значения эксцентриситета e . Указанный подход дает вполне удовлетворительные результаты, так как обычно нормальное функционирование происходит при величине e , не превышающей 0,3. Вид граничных условий и функции зазора допускает искать решение в форме разложения по малому параметру е и тригонометрического ряда по θ, для первой гармонической составляющей которого можно записать:

T ^{1 +a} ( r , 0 , t ) = — 0 ^+a ( r , t ) + e U ( r , t ) cos 0- V ( r , t ) sin 0] . (7)

Подставим данное разложение и выражение для функции зазора (1) в уравнение (2) и соберем члены уравнений, содержащие е в нулевой и первой степени. Выделим затем члены уравнений при sinθ и соsθ и получим следующую систему смешанных краевых задач:

соосное положение цилиндров ( e = 0):

для функции Ψ 0

^f H0 д^ T0+a dH0La dTa дr ^ 1 + a дr 2a -1 дr y v дт ,

1 +a

TV'l r = 0. t) = HA (r = 0, t) ,

f H0 W0+a -0+a дH„ )

1 + a д r    2a-1 д r

^{V                               J} r = 0

= 0 , T a ( r , t = 0 ) = 1;

эксцентричное положение:

для функции U

дf H0 д U U дH0 1 H0       a

I                          I U + Л t 0 V

дr V1 + a дr 2a-1 дr V 1 + a 1 + a

_5_f H1 9V0+a д r V1 + a д r

-0+a дH1 Л

2a-1 д r _v

+ Лv

a д

1 + a дт

[T 0U ]

U (r = p. t) = H^ Ho a (r = p. t) , I -HS- ди - -U- UH01 = 0, U (r, t = 0) = 0; a                V1 + a дr 2a-1 дr Jr=0

для функции V

Af _H0_ ^V^H01 - _H0_ V -A_^Ta U = Av      [T0V ],

дr V1 + a дr 2a -1 дr J 1 + a      1 + a          1 + a дтL

V(r = e,t) = 0,1 -H^дт

V1+aдr

V д H ₀ 1 2 a- 1 д r J _r = 0

= 0, U ( r , т = 0 ) = 0 ,

^2a-1         T ,                           a- 1

2a-1_.

где H _o = [1 + E_o cos2 k ( t + r ) ] ^a , H =------ [1 + E _ocos2 n ( T + r ) ] ^a

Уравнение (8) является нелинейным, уравнения (10) и (12) линейны относительно искомых переменных, но наличие в уравнениях перекрестных членов приводит их, по сути, на уровень нелинейных.

Нагрузочные способности сжимаемого слоя. Используем для решения нелинейной смешанной краевой задачи (8)–(9) итерационную схему с линеаризацией по методу Ньютона и итерационный процесс строим по схеме [8, 9]

L- o(^ n+1) = L- o(^ n) - L (’n), (14) где L.0 - производная Фреше от пространственно-временного дифференциального оператора L, определяемого уравнением (8),. 0 - начальное приближение для искомой функции давлений, .n и .n+1— n и n+1 итерационное приближение. В результате уравнению (8) соответствует сле- дующее итерационное уравнение:

д . dr

1 2 -а

-[ H ~ а

5.0а ’n+1 (1 + а) ~ аф dr       2а-1 0 n+1

2 а - 1

^d H “ ] -Л#’^»₊ Н ^{1 - а}

dr        v дт n+1

=-Уг о ^а - ^{(1 +} а ) * а ф ан F H^а ■'■. ^, " ( ¹ + а ) _ф а Н а d r | ^[ а ⁽         dr     2а - 1  ^{0 n}    dr  ^{)]  (} 1 + а dr   2а - 1 ⁿ      dr

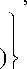
в котором введено обозначение . = . ^а .

Для построения дискретных уравнений использована идея балансных методов [10–12]. Для задач (10)–(13) получены трехточечные конечно-разностные уравнения, причем перекрестные члены уравнений (10) и (12) отнесены на предыдущий временной слой. Процедура решения аналогичной задачи уже была изложена нами в работах [5, 8] и здесь не приводится. В результате численного решения определяем избыточное давление в слое:

A P ( r , 0, т) = P ( r , 0, т) -1 = / {. ₀ ^{1 +а} ( r , т ) + e [ ^ ( r , t )cos 9- V ( r , T)sin 9 ] } ^{1 +а} / H ( r , 9, т) ^а ) -1, (16)

где Н ( r , θ, τ ) – функция зазора с бегущей волной, определяемая выражением (1).

При соосном положении ограничивающих цилиндрических поверхностей зазора (концентричный зазор) безразмерное давление определяется более просто:

P(r, т) = .0/ H а,(17)

а среднее за период бегущей волны избыточное давление равно

APc (r) = J (P (r, т) -1) d т.(18)

Для оценки нагнетательных свойств зазоров используем величину перепада среднего за период бегущей волны давления

AP = AP; (0)-APc (p).(19)

Проекции сил реакции двухфазного слоя на линию центров и линию ей перпендикулярную (см. рис. 1) вычисляем по формулам:

, P 2n _

Fe = Fe / <2p0RB) = — J J APC(r,9)Re(exp(jtot))d9dr,(20)

2 ^е 0 0

, p 2n _

Fy= FY /(2PRB) = — J J APc (r, 9)Jm (exp( jto t))d 9dr ,(21)

2 ^е 0 0

Соответствующие жесткости слоя равны:

Cе =Fe / е, Сγ =Fγ / γ, γ = arctg (Fγ / Fe),(22)

где e – эксцентриситет, γ – угол положения (см. рис. 1).

Расчет и конструирование

Результаты расчетов. В работе [8] автором рассмотрены нагнетательные свойства газовых слоев (α = 1) с бегущей волной. Показано, что зависимости среднего по времени перепада давлений имеют выраженный нелинейный характер, при этом максимум нагнетаемых давлений наблюдается в диапазоне малых значений частотного параметра (рис. 2). В отличие от зазоров, за-

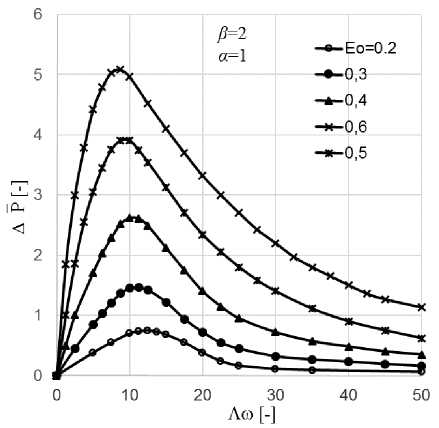
Рис. 2. Перепад средних по времени давлений в газовом слое с бегущей волной

сжимаемого слоя от параметра сдавливания

полненных несжимаемой жидкостью [6, 7], где в условиях неразрывности среды происходит непрерывный рост давлений при увеличении Λ ω , для сжимаемой среды при больших Λ_ω нагнетание среды не происходит. Увеличение параметра Λ ω соответствует увеличению скорости бегущей волны, при этом пропорционально скорости возрастают силы вязкого трения, препятствующие течению среды, и при достаточно больших Λ_ω течение будет отсутствовать, а действие бегущей волы сведется к обычному сдавливанию сжимаемого слоя с частотой волны [2]. Очевидно, что такой характер поведения нагнетаемых давлений должен существенно влиять на несущую способность и жесткость слоя, поэтому рассмотрим процессы в сжимаемом слое жидкости при эксцентричной форме зазора, определяющей кинематику нагружения тонкого слоя смазки.

Были рассчитаны зависимости жесткости Λω (без учета вращения цилиндров Λ=0 ), пред- ставленные на рис. 3. В диапазоне значений

Λω = 5...20 ранее были получены значительные уве-

личения средних по времени давлений (рис. 2), однако это, как оказалось, не привело к увеличению интегральных характеристик слоя. Более того, данные зависимости жесткости совпадают с соответствующими зависимостями для обычного цилиндрического вибронесущего слоя с равномерными по площади колебаниями [1, 2] (отметим только, что кривые выходят в зону асимптотического поведения при значениях Λω , в 2...3 раза превышающих значения Λω для обычного

слоя).

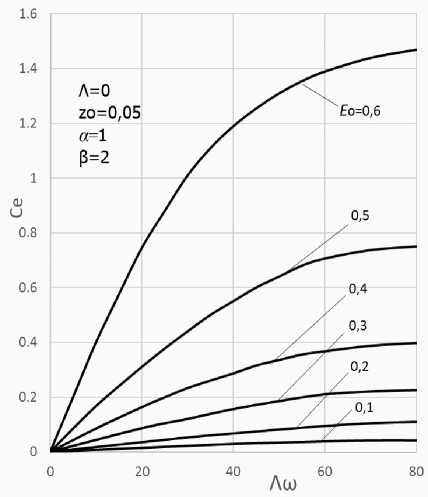
Рис. 3. Жесткость слоя с бегущей волной

Таким образом, увеличение давлений для полноохватных слоев, в отличие от неполноохватных, например, плоского кругового слоя, не приводит к увеличению интегральных характеристик.

Вращение поверхностей приводит к существенному изменению поведения интегральных характеристик.

На рис. 4а представлено распределение давлений вдоль оси при разных значениях угловой координаты. Видим, что распределение давлений без вращения поверхностей (Λ_ω = 20, Λ= 0) и с вращением (Λ_ω = 20, Λ = 10) значительно отличаются, при этом максимальный перепад давлений по угловой координате наблюдается на периферии слоя без вращения поверхностей и в плоскости симметрии – при вращении. Вращение в четыре раза увеличивает угловой перепад давлений и, следовательно, повышает несущую способность и жесткость слоя.

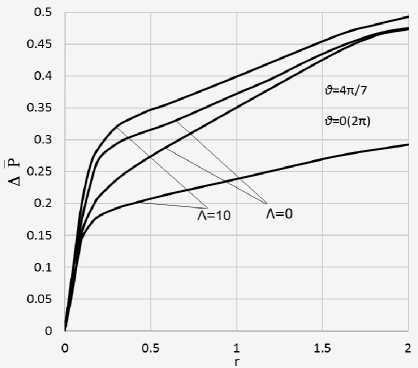
а)

Рис. 4. Распределение средних по времени избыточных давлений в газовом слое с бегущей волной при вращении ограничивающих слой поверхностей: а – влияние вращения; б – влияние частоты волны

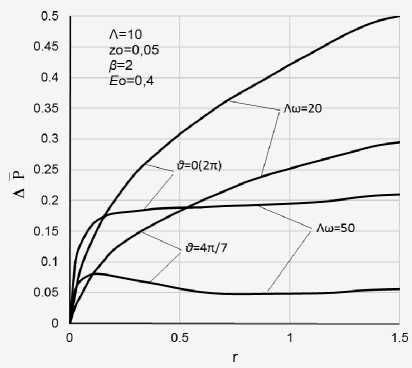
б)

Влияние скорости движения бегущей волны (параметр Λ_ω ) при вращении поверхностей зазора ( Λ = 10) можно проследить на рис. 4б. Очевидно, что для Λ_ω= 20 величина перепада давлений по угловой координате несколько больше, чем для Λ_ω = 50 и, кроме того, значительно больше сами величины нагнетаемых давлений, что можно объяснить близостью к экстремальным значениям давления при Λ_ω ≈ 10 (см. рис. 2).

Интегральные характеристики слоя представлены на рис. 5. На рис. 5а представлены зависимости проекций жесткости на линию центров Се и линию ей перпендикулярную С γ в зависимости от безразмерной длины слоя β в диапазоне значений β = 0,5...2. Как видим, в рассматриваемом диапазоне значений β наблюдается увеличение проекции жесткости на линию центров и незначительное уменьшение С γ. Аналогичные зависимости наблюдаются и для обычных вибронесущих слоев, однако крутизна представленных кривых существенно выше, что можно объяснить влиянием увеличения давлений в зазоре.

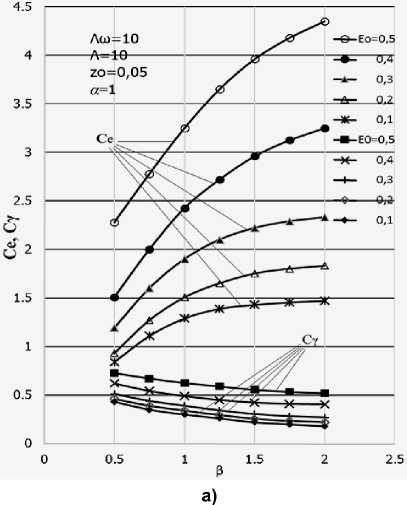
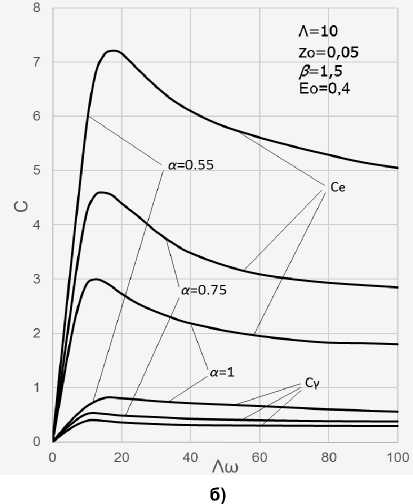
Рис. 5. Жесткость цилиндрического сжимаемого слоя с бегущей волной в зависимости: а – от длины зазора; б – от частоты волны

Расчет и конструирование

Еще большее увеличение интегральных характеристик происходит с уменьшением параметра газосодержания а. На рис 5б представлены зависимости жесткости Се и С y , которые показывают, что максимум той и другой жесткости наблюдается в том же диапазоне Λ_ω , где существуют максимальные значения перепада давлений. Очевидно, что участие вибронесущего эффекта здесь минимально, а основную роль играет сочетание высоких давлений, нагнетаемых встречно направленными бегущими волнами, и газодинамического эффекта со значением параметра сдавливания Λ= 10 [13]. Наиболее впечатляющим является влияние параметра газосодержания α, уменьшение которого приводит к теоретически бесконечным значениям жесткости слоя и столь же бесконечным уровням потребления энергии, затрачиваемой на сдавливание слоя. В данном рассмотрении используется кинематическое возбуждение слоя, поэтому энергетические аспекты остаются за пределами рассмотрения, хотя они и очевидны.

Заключение. Жесткость цилиндрического сжимаемого смазочного слоя, включающего симметричные встречно направленные бегущие волны, в различных условиях функционирования имеет значительные особенности.

• •    Действие бегущих волн в слое определяет появление радиальной и угловой жесткости, которые не имеет особенностей как в диапазоне частот бегущей волны, в котором наблюдается максимум нагнетаемого давления, так и за ним, при этом зависимости жесткостей повторяют аналогичные зависимости обычного цилиндрического вибронесущего слоя с равномерным вибрационным сдавливанием сжимаемой смазки. Графические зависимости жесткости от частоты выходят в зону так называемого «асимптотического» поведения [1] при значениях частоты движения бегущей волны, более чем в 2 раза превышающих аналогичные значения частоты нормальных зазору колебаний вибронесущего слоя с равномерным сдавливанием. Отсюда следует, что действие бегущей волны в циклических сжимаемых слоях смазки аналогично действию нормальных зазору равномерных колебаний и при достаточно больших частотах, когда движение смазки уже отсутствует (слой заперт), происходит обычное периодическое сдавливание слоя при разных угловых сдвигах по пространственной и временной координате.

• •    Добавочное вращение ограничивающих слой поверхностей с достаточно большой угловой скоростью приводит к появлению развитого эффекта «клина» [2], который в комбинации с эффектом нагнетания смазки от действия бегущей волны приводит к появлению комбинационных мультипликативных эффектов. В частности, в диапазоне частот бегущей волны, в котором наблюдается максимум нагнетаемого давления, происходит существенное увеличение жесткостей, определяемых эффектом клина: для газового смазочного слоя радиальная жесткость почти в два раза превышает жесткость без дополнительного нагнетания газа, а при больших частотах движения бегущей волны, т. е. в зоне асимптотического поведения слоя, полученные расчетные значения жесткости также являются комбинационными (взаимодействуют эффекты сдавливания и клина) и численно совпадают со значениями полученными, например, в работах [2, 13].

• •    Сочетание участков зазора с бегущей волной и участков развитого эффекта сдавливания смазочного слоя с равномерными нормальными зазору колебаниями также приводит к появлению комбинационных эффектов и, в частности, для обозначенного выше типового цилиндрического сопряжения, имеющего дополнительный участок сдавливания газового слоя в центре симметрии этого сопряжения, на частотах движения бегущей волны, определяющих максимальные значения давлений, радиальная жесткость тоже почти в два раза превышает аналогичные значения этого же участка смазочного слоя с обычным равномерным сдавливанием. Это значение соотносится с результатом на основе эффекта клина и подчеркивает тот факт, что эффект сдавливания является, по сути, его разновидностью.

• •    Влияние сжимаемости смазки проявляется в том, что с уменьшением доли газа, а значит и параметра газосодержания α , величины нагнетаемых давлений [8] и жесткости слоя возрастают и, например, при а = 1/4 они уже более чем на порядок превышают аналогичные значения газовых слоев смазки. Дальнейшее исследование характеристик сжимаемого слоя смазки с величиной а <  1/4 на предложенной математической модели связано со значительными вычислительными трудностями и лучше перейти на модель несжимаемой смазки с учетом проявлений сжимаемости [14–19], при этом надо учесть, что для несжимаемой смазки эффект сдавливания слоя не существует или, если использовать энергетическую трактовку, для его реализации требуется источник питания бесконечно большой мощности.

Действие зазоров с бегущей волной в устройствах триботехнического типа сводится в основном к эффекту нагнетания среды в смазочный слой, и пьезоактивный привод можно было бы в некоторых реализациях с успехом заменить на внешнее нагнетательное устройство подобно гидростатическим опорам. Однако при таком подходе получаем устройство другого класса, так как полностью теряется основное преимущество вибронесущих опор – автономность и компактность.

Область применения устройств на их основе к настоящему времени является достаточно узкой, так как они не могут конкурировать с обычными гидродинамическими и даже газодинамическими подшипниками из-за сложностей и особенностей реализации резонансных вибропреобразователей, требующих электронной системы питания. Эта проблема в радиотехнике и электротехнике давно решена созданием различного типа устройств с автоматической подстройкой частоты (АПЧ) на заданный сдвиг фаз нагрузки, максимум потребляемой мощности и т. д. Здесь же требуется разработка специализированных многоканальных импульсных усилителей мощности, согласующих фильтров, устройств АПЧ. Самодельные устройства в промышленных применениях эту проблему закрыть не могут.

Модульный принцип должен быть заложен и при изготовлении различных частей зазоров опорных узлов и изобретение автора (а.с. № 1225310 A, F 16 C 17/02, 1984) дает все основания для этого. В нем реализована конструкция вибропреобразователя цилиндрического типа, состоящего из пакета виброизолированных друг от друга пьезоактивных преобразователей кольцевой формы. Подключение набора таких преобразователей к многофазному генератору-усилителю (не будем здесь обсуждать его особенности) на одной из собственных частот радиальных колебаний кольцевых преобразователей [8] позволяет реализовать в зазоре бегущие волны, а подключение другой части пакета к однофазному генератору опять же на одной из радиальных форм колебаний с достаточно высокой собственной частотой обеспечит равномерное сдавливание слоя сжимаемой смазки и развитый вибронесущий эффект. Эти зоны можно комбинировать между собой, получая тем самым желаемые виброреологические характеристики [20] подвеса или подшипника.

Другой важной составляющей этой проблемы является задача создания сжимаемой смазочной среды. Подобно создаваемым современным материалам нужно создавать и жидкости с заданными свойствами и, в частности, с заданной сжимаемостью. Тогда при достаточно большой мощности источника питания можно, как было показано выше, многократно увеличить основные интегральные характеристики опорных узлов. Альтернатива решения этой задачи в виде дополнительного газирования или создания в слое развитого поля ультразвуковой кавитации не дает стабильных параметров среды и является, по сути, случайной, что лишает, на наш взгляд, это направление перспектив.