Улучшение сейсмического изображения на этапе интерпретации для решения задач сейсмофациального анализа

Для геометризации литологических ловушек в процессе интерпретации сейсмических данных одним из главных условий является наличие качественного сейсмического изображения, получение которого достигается сложением и умножением усилий на каждом этапе сейсмических исследований: от грамотного планирования полевых работ и их качественного проведения до тщательной обработки зарегистрированного волнового поля с последующим корректным применением разнообразных трансформаций на этапе интерпретации.

Качество исходных сейсмических данных во многом зависит от сейсмогеологических условий. Например, в Западной Сибири, по заключению А.А. Нежданова, информативность сейсмической записи резко снижают неоднородности строения верхней части разреза, обусловленные наличием многолетнемерзлых пород переменной толщины и присутствием низкоскоростных прослоев. В связи с этим в северных регионах Западной Сибири разрешающая способность данных сейсморазведки МОГТ априори ниже, чем в южных регионах и в районах Среднего Приобья, где глубины залегания продуктивных комплексов значительно меньше, а верхняя часть разреза имеет более однородное строение [1].

Одним из наиболее критичных факторов в изучении геологических седиментационных объектов является ограничение разрешающей способности сейсморазведки как дистанционного геофизического метода исследований. Применительно к задачам сейсмофациального анализа крайне важное значение имеет понимание механизма формирования сейсмического отклика в конкретных сейсмо-геологических условиях [2], учитывая тот факт, что большинство отражений представляет собой результат интерференции сигналов, отраженных от серии близкорасположенных акустических границ, а также наличие в исходном волновом поле разнообразных помех, способных исказить или завуалировать регистрируемые отражения.

Соотнесение геометрии изучаемых объектов с разрешающей способностью сейсморазведки позволяет определиться с приемами и методами работы, направленными на улучшение сейсмического изображения.

В данной статье затронута тема улучшения сейсмического изображения на этапе интерпретации сейсмических данных. Авторы статьи предлагают рассмотреть два направления. Первое направление касается использования возможных средств постобработки волнового поля. В статье приведен обзор причинно-следственных связей эффективного применения частотно-зависимых атрибутов. Второе направление связано с визуализацией данных и их возможной трансформацией инструментами обработки непосредственно статичных изображений. Для иллюстрации отдельных положений и выводов авторы фокусируются на таких седиментационных объектах, как палеоканалы [3].

Разрешающая способность сейсмического метода

Под разрешающей способностью сейсмических исследований понимается способность различать близкорасположенные объекты в двух направлениях: по вертикали (по времени и глубине) и по горизонтали (от трассы к трассе). Ключевым параметром в определении разрешающей способности метода является длина волны. В практических исследованиях длина волны варьирует в широких пределах — от 15 до 300 м [2], увеличиваясь с глубиной вследствие изменения скоростных характеристик среды в сторону повышения и снижения частоты колебаний . Основная часть энергии сейсмического импульса приходится на некоторую полосу частот, в центре которой оценивается доминирующая частота. В производственных исследованиях спектр характеризуется полосой частот от 7 до 120 Гц.

Обозначенные параметры связаны следующим соотношением:

длина волны X = скорость * период = скорость/частота.

Разрешающая способность по вертикали [2] оценивается в 1/8–1/4 длины волны. Р.Е. Шерифф допускает, что при простом строении среды, наличии четко выраженного опорного горизонта и при условии минимума помех возможно различать и более близкорасположенные границы. Обращает на себя внимание замечание этого автора о том, что разрешающую способность можно отнести к субъективным характеристикам, так как она зависит, в том числе, и от способности интерпретатора улавливать незначительные изменения формы сигнала. В современных реалиях эта способность тесно увязывается с профессиональным владением инструментами трансформации исходных данных (постобработки) для повышения качества сейсмического изображения.

На рис. 1 для акустически контрастного пласта на модельных данных продемонстрировано отношение длины волны и формы трассы при условии нульфазового импульса [4]. Рассмотрено два варианта. В первом варианте (см. рис. 1 A) кровле и подошве пласта соответствуют разноименные экстремумы (min/max), во втором варианте (см. рис. 1 B) — одноименные (max/max). Для первого варианта разрешенность оценивается в W4 (X — длина волны) [5-8]; для второго варианта — X/4,6 [9].

Для практических исследований динамической интерпретации и прогноза коллекторских свойств наиболее предпочтительными считаются сейсмические данные, приведенные к нульфазо-вому импульсу [8], так же как и в рассмотренном модельном примере. В качестве обоснования выдвигаются следующие положения: форма импульса симметричная, большая часть энергии сосредоточена в центральном экстремуме, экстремум соот-

ГЕОФИЗИЧЕСКИЕ ИССЛЕДОВАНИЯ

Рис. 1. Два варианта модели клина [4]

Fig. 1. Two versions of wedge model [4]

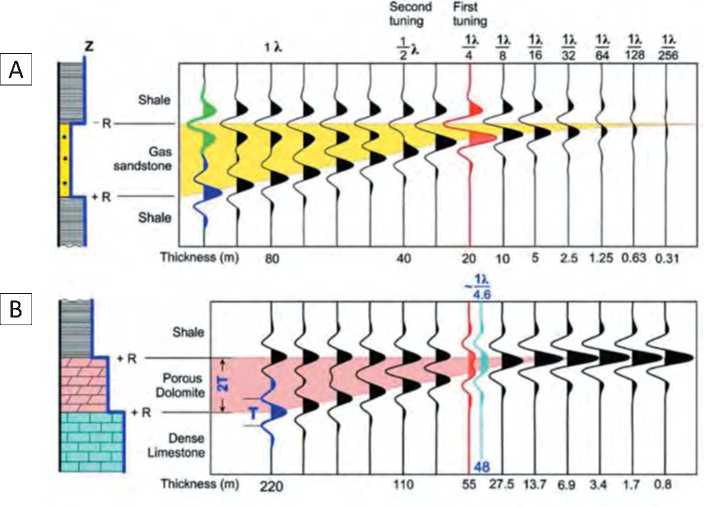
ветствует непосредственно акустической границе и совпадает с временным горизонтом, разрешен-ность данных выше, чем при использовании других форм импульса в том же частотном диапазоне. Однако реальные сейсмические импульсы в основном являются минимально-фазовыми (или близкими к таковым). Р.Е. Шерифф отмечает, что от формы элементарного импульса зависит, как будет выглядеть сложный сигнал, однако она не влияет непосредственно на разрешающую способность, если изменение не связано с изменением частотной характеристики.

Предел «видимости» (разрешенности) зависит в первую очередь от степени акустической контрастности кровли и подошвы пласта, а также общей зашумленности данных (рис. 2).

В табл. 1 [8] демонстрируется матрица из 20 различных ситуаций, иллюстрирующая широкий возможный диапазон разрешения данных. Некоторые постпроцессинговые трансформации позволяют получать дополнительную геолого-геофизическую информацию при разложении интерференционных сигналов на отдельные их составляющие и таким образом влиять на улучшение разрешенности сейсмической записи.

Наилучшим образом возможности разрешающей способности сейсмического метода демонстрируют синтетические модели.

На рис. 3 представлены результаты двухмерного синтетического моделирования. Геологическая основа создана в соответствии с современными аналогами фациальной модели сечения барьерного острова с приливно-отливным каналом. Литофации представлены песчаниками барьерного острова в виде двух прослоев во вмещающей их глинистой толще — песчаниками приливно-отливной отмели и аргиллито-алевролитовыми разностями, заполняющими приливно-отливной канал. В первой модели (см. рис. 3 B) использовался вейвлет с доминирующей частотой 20 Гц, во второй (см. рис. 3 C) — вейвлет с доминирующей частотой 35 Гц. Результаты моделирования показывают, что данные с частотой 20 Гц не отображают деталей геологического строения, заложенных изначально в модель. Два слоя песчаного коллектора, как и другие детали разреза, могут быть идентифицированы только на сейсмических данных с частотой 35 Гц. Выполненное моделирование позволило в процессе переобработки данных сфокусироваться на получении финальных разрезов с доминирующей частотой 35 Гц [10].

На рис. 4 продемонстрированы результаты синтетического моделирования системы палеоканалов. В модель заложены следующие параметры: ширина одного канала составляет 150 м (15 трасс), максимальная мощность одного канала составляет 8 м, область тонкого переслаивания песчаника существует в трассах 12-15 и 23-26. Мощности области вертикального наложения фаций палеоканалов составляют 3 и 4 м. Синтетическая модель рассчитывалась с доминирующей частотой 50 Гц (вейвлет Рикера, шаг дискретизации — 1 мс) [11].

Для палеоканалов в кровле тюменской свиты по результатам двухмерного сейсмогеологического моделирования установлено, что резкое увеличение толщин песчаников (от 0 до 25 м) может быть зафиксировано на сейсмических временных разрезах при рабочих частотах около 40 Гц и оно прак-

GEOPHYSICAL SURVEYS

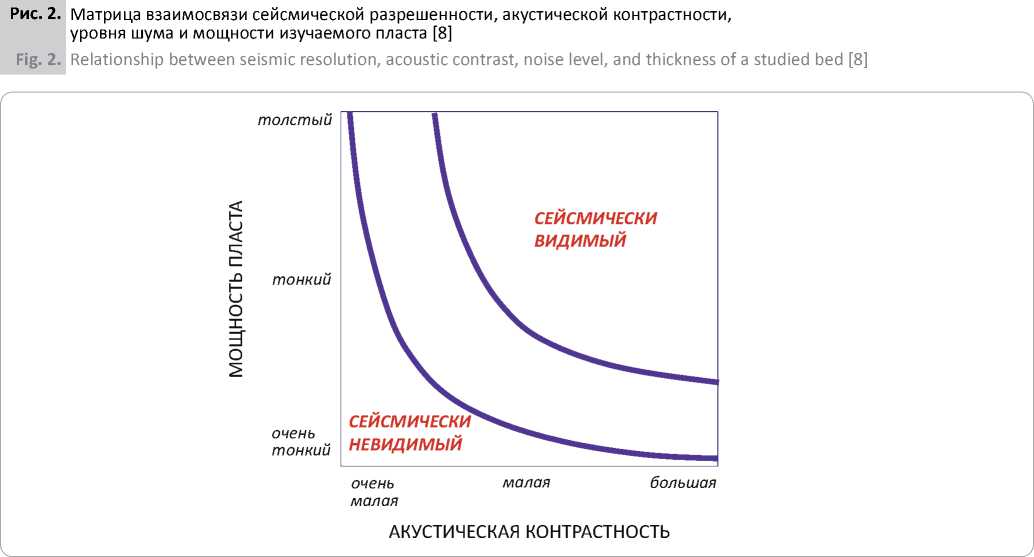
Табл. 1. Отличия в разрешающей способности при различных сейсмогеологических условиях [8]

Tab. 1. Comparison of resolution in different geoseismic conditions [8]

Возраст пород Очень молодые Молодые Средние Древние Очень древние Глубина залегания Очень малая Малая Средняя Глубокая Очень глубокая Скорость волны в горной породе, м/с 1600 2000 3500 5000 6000 Доминирующая частота, Гц 70 50 35 25 20 Длина волны, м λ 23 40 100 200 300 Предел «разделимости» λ/4 6 10 25 50 75 s 1- о S m c; OJ ^ OJ IZ Низкое отношение сигнал/ помеха Песчаник, насыщенный водой. Данные низкого качества ~λ/8 3 5 13 25 38 Среднее отношение сигнал/ помеха Песчаник, насыщенный водой/нефтью. Достаточно хорошее качество данных ~λ/12 2 3 8 17 25 Высокое отношение сигнал/ помеха Песчаник газовый. Хорошее качество данных ~λ/20 1 2 5 10 15 Очень высокое отношение сигнал/ помеха Песчаник газовый. Отличное качество данных ~λ/30 < 1 1 3 7 10 тически не проявляется на более низкочастотных разрезах [1].

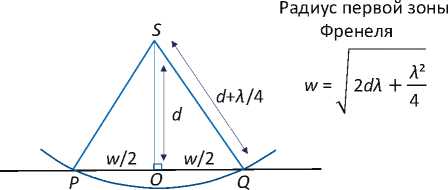
Разрешающая способность сейсмического метода по латерали определяется шириной первой зоны Френеля. Для оценки горизонтального разрешения использовались формулы следующих авторов: Денхам (1980), Клербоут (1985), Эмбри (1985), Фрилэнд, Хогг (1990), Эбром и др. (1995), Вермеер (1997) и др.

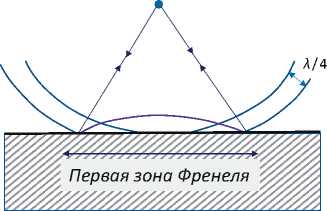
Представление о том, что отраженный сигнал генерируется не точкой, а некоторым фрагмен- том отражающей поверхности, является основой для понимания разрешающей способности метода (рис. 5, 6).

Размеры зоны Френеля зависят от частоты, так как частота влияет на длину волны (рис. 7). Следовательно, разным частотным компонентам сейсмической волны будут соответствовать разные по величине эффективной площади участки отражающей поверхности [2]. Например, в случае плоской отражающей поверхности, расположенной на глубине 1000 м при скорости сейсмических волн 2000 м/с,

ГЕОФИЗИЧЕСКИЕ ИССЛЕДОВАНИЯ

Рис. 3. Седиментационная модель (A) [10] и результаты синтетического моделирования (B, C)

Fig. 3. Depositional model (A) [10] and results of synthetic modelling (B, C)

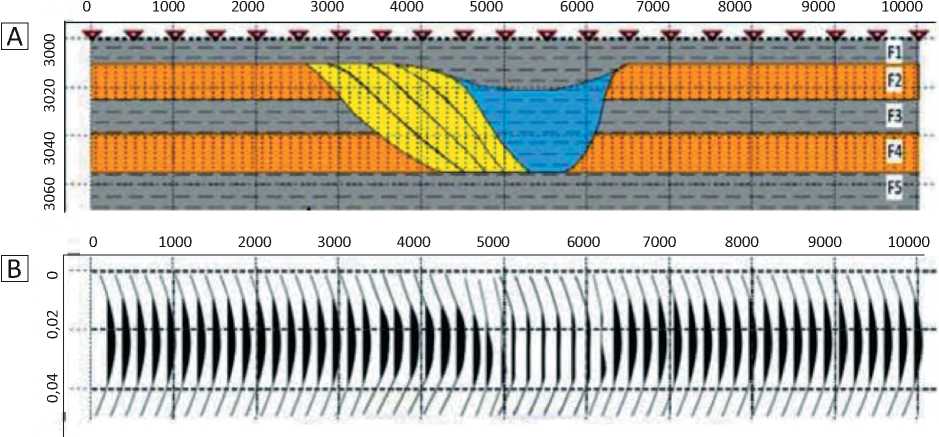
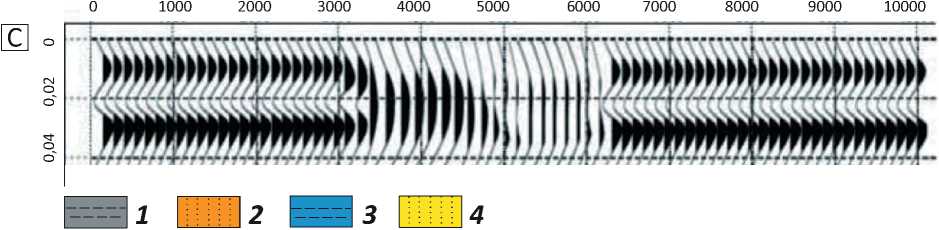
A — геологическая модель; результаты синтетического моделирования после сдвига фазы на 90° с доминирующей частотой, Гц: B — 20, C —35.

1 — глинистые отложения (слои F1, F3 и F5 мощностью 10, 13 и 15 м соответственно, скорость 2500 м/с);

2 — песчаники барьерного острова (слои F2 и F4 мощностью 15 и 16 м соответственно, скорость 3800 м/с);

3 — приливно-отливной канал (мощность 40 м, скорость 2900 м/с); 4 — приливно-отливная отмель (мощность 45 м, скорость 3500 м/с)

A — geological model; results of synthetic modelling after phase shift by 90° with a dominant frequency, Hz: B — 20, C — 35.

1 — argillaceous deposits (F1, F3, and F5 beds 10, 13, and 15 m thick, respectively, velocity 2500 m/s); 2 — barrier island sandstone (F2 and F4 beds 15 and 16 m thick, respectively, velocity 3800 m/s); 3 — distributary/tidal channel (40 m thick, velocity 2900 m/s); 4 — tidal flat (45 m thick, velocity 3500 m/s)

радиус первой зоны Френеля будет равен 130 м для волнового поля с частотой 60 Гц и 183 м для волнового поля с частотой 30 Гц. Размер зоны Френеля зависит также от расстояния до точки наблюдения ( d ) и кривизны отражающей поверхности.

Для условий Западной Сибири (при целевом интервале на 2,5 с, частоте 30–40 Гц, скорости 3,5– 4 км/с) ширина зоны Френеля составляет в среднем 450–600 м [1]. Существуют общие теоретические представления, применяемые в определении предельных размеров поисковых объектов при наблюдениях по методике многократных перекрытий, которые сводятся к значениям, равным 1/4 первой зоны Френеля. Для палеоканалов, идентифицируемых в отложениях тюменской свиты, ширина, как правило, составляет от 100 до 500 м.

В качестве основного метода улучшения горизонтального разрешения используются миграционные преобразования, направленные на смещение отражения в точку его изначального формирования; фокусировку энергии, распределенную по зоне Френеля, и нивелирование дифракционных эффектов, возникающих от отдельных неоднородностей среды. Очевидно, что наибольший эффект от применения миграции достигается для трехмерных сейсмических данных. Точность миграционных преобразований зависит от корректности скоростной модели, отношения сигнал/шум, выбранной апертуры миграции и конкретного алгоритма.

В работе [8] основные факторы, оказывающие влияние на разрешающую способность сейсмического метода, сведены в блок-схему (см. рис. 7).

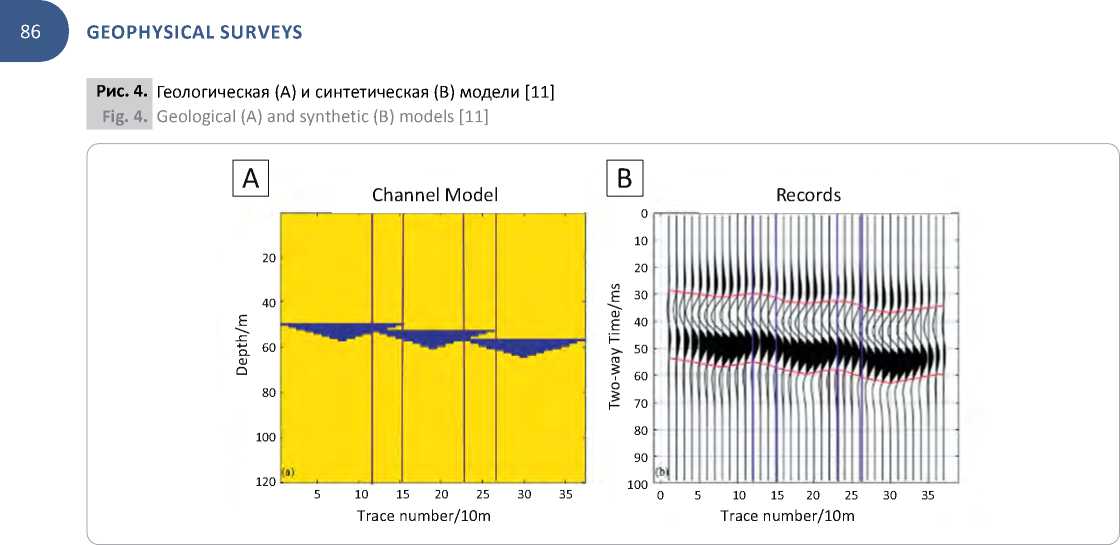
Рис. 5. Определение радиуса первой зоны Френеля [2]

Fig. 5. How the first Fresnel zone radius is determined [2]

Источник и приемник

Повышение качества сейсмического изображения на этапе интерпретации

Анализ разрешающей способности сейсмических исследований позволяет сделать вывод, что улучшение сейсмического изображения, повышение его детальности во многом определяется частотными характеристиками. Параметры амплитудно-частотного спектра являются важными индикаторами в процессе интерпретационного сопровождения обработки [12]. Доминирование низких частот в амплитудно-частотном спектре ведет к потере детальности сейсмогеологической интерпретации, однако трансформации, направленные на приоритетное выделение высоких частот, могут привести к расфокусировке опорных (условных) отражающих горизонтов.

На этапе интерпретации сейсмических данных работа с частотными характеристиками волнового поля может осуществляться через расчет соответствующих атрибутов и декомпозицию волнового поля по частотам.

Частотные атрибуты в библиотеке ПО Petrel

Instantaneous frequency (мгновенная частота) — характеризует скорость изменения фазы. Сейсмическое изображение атрибута смотрится достаточно разрешенным по сравнению с исходными амплитудными разрезами. Например, может выгодно подсветить на разрезе внутреннее строение клиноциклита. Однако параметр имеет тенденцию быть нестабильным в присутствии шума и его достаточно трудно интерпретировать.

ГЕОФИЗИЧЕСКИЕ ИССЛЕДОВАНИЯ

Рис. 6. Влияние частоты колебаний на размер зоны Френеля [2] Fig. 6. Oscillation frequency influence on the Fresnel zone size [2]

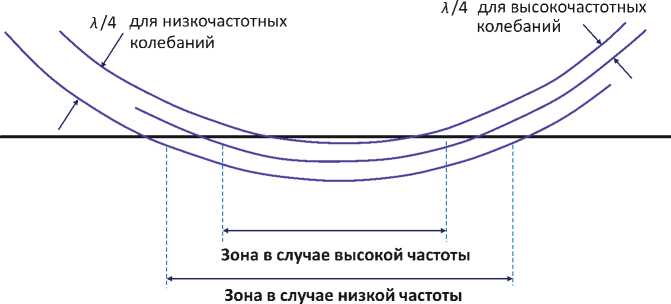
Рис. 7. Факторы, влияющие на разрешающую способность сейсмического метода [8]

Fig. 7. Factors influencing the seismic method resolution [8]

Высокие частоты при максимальной кратности регистрации данных

Миграция (2D или 3D)

Повышение отношения сигнал/помеха

Разрешающая способность

Горизонтальный минимальный размер ( выборка зоны Френеля )

Вертикальная минимальная мощность (импульс)

Деконволюция

Instantaneous bandwidth (Мгновенная ширина полосы частот). Атрибут отражает стандартное отклонение ширины мгновенного спектра от его среднего значения, представляет собой меру интенсивности относительного изменения мгновенной амплитуды.

Dominant frequency (Доминантная частота) определяется как корень квадратный от суммы квадратов Instantaneous frequency и Instantaneous bandwidth . Данную трансформацию исходного разреза можно использовать для обоснования сейсмо-стратиграфических комплексов, картирования поверхности фундамента и др.

Instantaneous bandwidth и Dominant frequency дополняют Instantaneous frequency . Совместно эти три атрибута представляют собой переменные во времени спектральные свойства сейсмических данных. С их помощью можно картировать низкочастотные области с нечеткими очертаниями.

Frequency filter (частотный фильтр) — атрибут позволяет усилить конкретное событие в волновом поле за счет переменной во времени фильтрации, сопровождается библиотекой фильтров низких, высоких частот, фильтрами Баттерворта, Ормсби и др.

Graphic equalizer — является интерактивным фильтром и позволяет получить сейсмический массив данных в выбранной полосе частот. На основе заданных пользователем параметров алгоритм рассчитывает индексированную весовую функцию для усиления или уменьшения выбранной частотной составляющей исходного сигнала.

t*Attenuation ( t *Затухание) — атрибут, вычисление которого основывается на оценке затухания частот в заданном окне. Физический смысл параметра для трещиноватого коллектора связывают с наличием трещин открытого типа и их плотностью (алгоритм запатентован компанией Шлюмберже).

Iso-frequency — запатентованная компанией Шлюмберже методика сейсмической декомпозиции, в процессе которой создается набор кубов атрибутов на заданных пользователем частотах.

Generalized Spectral Decomposition (обобщенное спектральное разложение) — атрибут позволяет раз-

GEOPHYSICAL SURVEYS

Рис. 8. Частотные атрибуты [8]

Fig. 8. Frequency attributes [8]

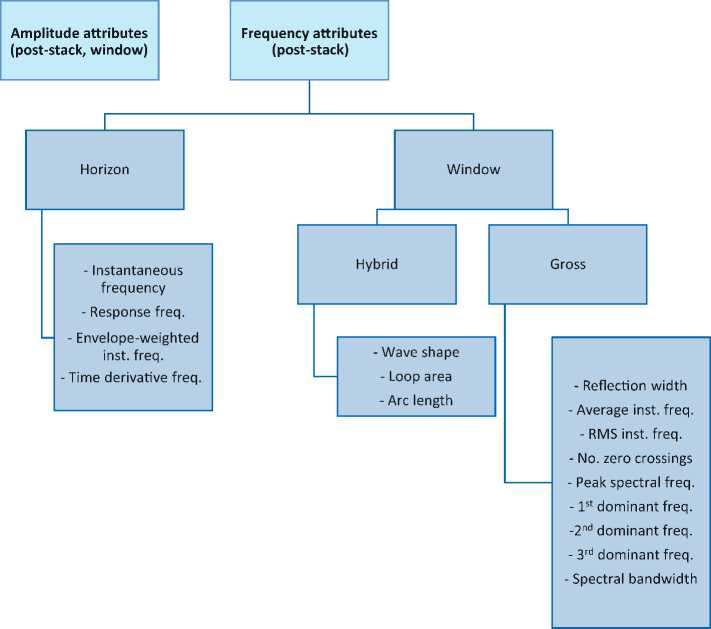
ложить сейсмический сигнал на составляющие его частоты, помогая интерпретатору выявить геологические объекты, находящие отклик в волновом поле на определенной частоте. В алгоритме GSD используется гибридный подход, основанный на преобразовании Фурье (STFT) и непрерывном вейвлет-пре-образовании (CWT) [13].

Обобщающая таблица рассмотренных частотных атрибутов представлена на рис. 8.

Спектральная декомпозиция.

Приемы визуализации

В настоящее время спектральная декомпозиция активно применяется при интерпретации сейсмических данных, этот подход позволяет «проявить» на слайсах геологические объекты, которые существенно хуже распознаются при анализе стандартных амплитудных атрибутов, рассчитанных в обычной полосе частот. В процессе декомпозиции сейсмический сигнал раскладывается на ряд частотных составляющих, что позволяет проанализировать амплитуду и фазу, настроенные на заданную длину волны. Учитывая тот факт, что сейсмические отражения в слоистом разрезе являются результатом интерференции от нескольких близкорасположенных границ, а геологические объекты с различной мощностью, литологическим составом и насыщением имеют различный частотный отклик в полях упругих волн, то спектральное разложение позволяет извлечь уникальную информацию, связанную с локальными объектами. Для анализа частотных компонент сигнала используются такие методы, как оконное преобразование Фурье во временной области (Short Time Fourier Transform) [14, 15], непрерывное вейвлет-преобразование (Continuous Wavelet Transform) [16] в переменном диапазоне временного окна, декомпозиция максимального подобия (MPD) и др.

Наибольшую эффективность спектральной декомпозиции специалисты отмечают в процессе интерпретации сейсмических данных, вмещающих отклик от палеоканалов.

В статье [17] приведен классический пример применения спектральной декомпозиции для изучения русловых отложений. Автором обоснован тот факт, что «тонкие» участки русла наилучшим образом фиксируются в амплитудах, снятых по горизонту в полосе высоких частот, в то время как увеличенные мощности русловых отложений более отчетливо выражены в диапазоне низких частот. В статье [18] представлено наглядное схематическое изображение данного случая (рис. 9), на котором демонстрируется, что в краевых зонах палеоканала, где мощность отложений невелика, тюнинг-эффект наблюдается на спектральной компоненте высоких частот, в осевой части русла — в области максимальных значений мощности [19].

Известно, что изучение палеорусловых систем сейсморазведкой сопряжено с ограничениями в

ГЕОФИЗИЧЕСКИЕ ИССЛЕДОВАНИЯ

Рис. 9. Классический пример использования спектральной декомпозиции для изучения русловых отложений

Fig. 9. Textbook example of using Frequency Decomposition in riverbed deposit studies

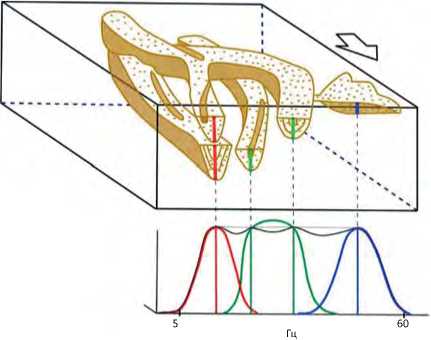
«Тонкие» участки русла наилучшим образом фиксируются в амплитудах, снятых по горизонту в полосе высоких частот, в то время как увеличенные мощности русловых отложений более отчетливо выражено в диапазоне низких частот (по [18], доработано авторами данной статьи)

“Thin” segments of riverbed are better seen in amplitudes taken along the horizon in high frequency band, while the segments of larger thickness are more clear in low frequencies (according to [18], modified by the authors)

латеральной и вертикальной разрешающей способности метода, так как для речных систем характерно многообразие фаций при незначительной мощности геологических тел. Например, типичными параметрами для изолированных меандри-рующих поясов можно считать мощность от 5 до 15–20 м, ширину — от 1 до 5 км; прирусловые валы рек имеют обычно высоту 0,5–1 м (у крупных рек редко до 5 м); у сформированных в периоды сильных паводков конусов прорыва (кревассов), сложенных пойменным аллювием, мощность составляет обычно 0,5–1, реже до 3 м. Аллювиальные системы отличаются крайней неоднородностью строения в силу того, что русла непрерывно трансформируются, претерпевая различные флуктуации. В связи с вышеизложенным, в волновом поле объект может проявляться фрагментарно, что затрудняет его интерпретацию. В большинстве случаев в сейсмическом изображении наблюдается интегральная картина сложного сочленения палеоканалов с частичным размывом и переотложением осадка, не отображающая современную морфологию речной палеосистем [20].

Одной из особенностей интерпретации результатов спектральной декомпозиции является синхронная визуализация, как правило, трех наиболее информативных амплитудных слайсов, полученных в разных полосах частотного диапазона при помощи аддитивной цветовой модели RGB (Red, Green, Blue — красный, зеленый, синий) (рис. 11). Технология визуализации является важным инструментом при интерпретации сейсмических данных, и, в случае спектральной декомпозиции, она сыграла ключевую роль в активном внедрении данного подхода. Схематическое пред- ставление спектральной декомпозиции и RGB-суммирования представлено на рис. 10.

Обработка цветовых изображений

Для улучшения разрешения цветовые изображения, получаемые в результате динамической интерпретации сейсмических данных, можно подвергнуть графической «дообработке». Для этого используются различные фоторедакторы, фильтрации, способы коррекции фотографий и рисунков, технологии компьютерного зрения, которые за последнее десятилетие получили широкое распространение.

В статье [21] представлено два способа фильтрации изображений, которые успешно зарекомендовали себя для картирования отложений типа «русло».

Первый способ основан на фильтрации изображения (карты какого-либо атрибута, где требуется найти «русло») с помощью библиотеки двухмерных импульсов Морле, также известных как фильтр Габора. Фильтр Габора широко применяется при обработке изображений со структурной избыточностью, имеющих квазипериодическую структуру, например при цифровом анализе отпечатков пальцев, выделении сосудов на изображениях биологических тканей.

Второй способ заключается в преобразовании каждого фрагмента изображения заданного размера в область Радона. Полученная таким образом «синограмма» отражает вероятность наличия линейной аномалии каждого направления на исходном фрагменте.

GEOPHYSICAL SURVEYS

Рис. 10. Принципиальная схема алгоритма спектральной декомпозиции и цветового (RGB) смешивания разночастотных компонент

Fig. 10. Schematics of Frequency Decomposition algorithm and RGB blending of components having different frequencies

Ориентация куба

Время

Исходный (0–125 Гц)

40–50 Гц

30–40 Гц

Рис. 11. Цветовая карта спектральной декомпозиции в визуализации RGB-смешивания и цветовые карты по отдельным цветам Fig. 11. Frequency Decomposition coloured map in RGB blending visualization and monochrome maps

ГЕОФИЗИЧЕСКИЕ ИССЛЕДОВАНИЯ

Рис. 12. Карта экстрагированных значений амплитуды Fig. 12. Map of extracted amplitude values

A — 20 мс вниз, B — 10 мс вниз

A — 20 ms down, B — 10 ms down

Авторы статьи [21] отмечают ограничение универсальности этих методов. Они позволяют выделить русла только заранее известной ширины, отличающиеся по амплитуде от вмещающих пород. В более сложных случаях (русло переменной ширины, русловая долина, пересекающиеся объекты) погрешность таких методик фильтрации изображений возрастает.

В статье [22] описан опыт применения криволинейного преобразования и морфологического фильтра для детектирования палеоканалов, показывающий хорошую способность изображения края кривой. Авторы подчеркивают, что именно сочетание морфологического градиента с криволинейным преобразованием позволяет более точно закартировать элементы палеоречной системы.

Развитие направления обработки цифровых изображений применительно к сейсмогеологи-ческой интерпретации, возможно, в будущем позволит решить задачу автоматизации процесса выделения палеоканалов. В настоящий момент на цветовых картах спектральной декомпозиции палеорусла выделяются вручную, что требует больших затрат времени, приводит к высокой неопределенности, так как ручная интерпретация достаточно субъективна, не учитывает индивидуальных особенностей зрительного восприятия.

Практический пример

Рассмотрим комплексный подход к интерпретации сейсмических данных для изучения палео-русловых систем тюменской свиты на примере одного из месторождений Ханты-Мансийского АО. Комплексирование полученной информации об изменчивости динамических характеристик волнового поля в пространстве позволило выделить и закартировать на площади исследования сеть

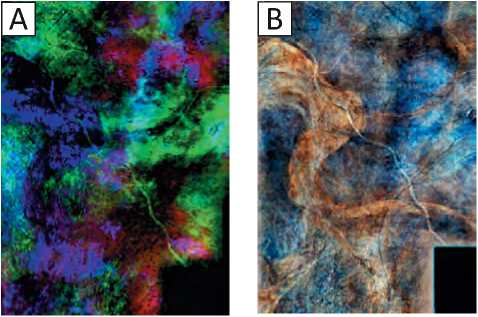
Рис. 13. Цветовые карты Fig. 13. Coloured maps

• 1    ГП 2    3

A — спектрального разложения, B — eXchroma.

1 — 15 Гц; 2 — 25 Гц; 3 — 35 Гц

A — spectral decomposition, B — eXchroma.

1 — 15 Hz; 2 — 25 Hz; 3 — 35 Hz палеорусел, изучение которых осложнено в связи с ограничениями разрешающей способности сейсмического метода. В данном примере были использованы следующие подходы сейсмофациального анализа.

• 1.    Атрибутный анализ поспособствовал экс-пресс-идентификации палеорусловых систем, позволил оценить качество исходных данных и характерные особенности шнурковых аномалий. Однако на картах отобразились только объекты, наиболее контрастно проявленные в волновом поле. В данной работе рассчитывались атрибуты, представленные в библиотеке ПО Petrel, вблизи ОГ T. Слайсы, демонстрирующие вариации амплитуд в пределах съемки 3D, представлены на рис. 12.

• 2.    Алгоритмы спектральной декомпозиции позволили в значительной степени уточнить конфигурацию и распространение палеорусел. Полученная схема представлена на рис. 13 A. Стоит отметить, что по сравнению с атрибутным анализом, русла и пояса меандрирования выделяются с более высокой степенью детальности и контрастности.

• 3.    Технология eXchroma, реализованная в ПО Petrel и заключающаяся в цветовом смешивании амплитудных срезов, сдвинутых относительно друг друга на дискреты по вертикали, позволила закартировать палеорусла с наиболее высокой степенью детальности. На изучаемой площади данная технология показала наиболее высокую степень детальности и информативности как для палеорусел, так и для поясов руслоформирования. Цветовая карта eXchroma представлена на рис. 13 B.

• 4.    Кластеризация по методу k -среднего применялась для фиксации наиболее критичных границ

  

  GEOPHYSICAL SURVEYS

  
  

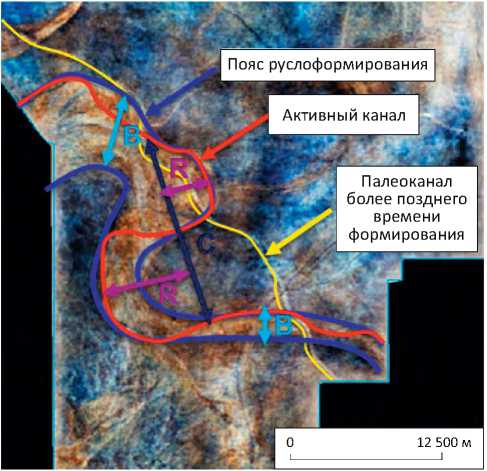
Рис. 14. Оценка морфологии палеорусла по параметрам синусоидальности Fig. 14. Judgmental estimate of paleo riverbed using harmonicity parameters

12 500 м

Пояс руслоформирования

Активный канал

Палеоканал более позднего времени формирования

в вариациях сейсмических атрибутов, что способствовало картированию характерных объектов и определению границ фациальных обстановок.

Оценка информативности перечисленных подходов происходила в процессе работы, в основном на экспертном уровне.

Применение вышеперечисленных подходов позволило закартировать в пределах целевого интервала несколько палеорусел. Для наиболее контрастно проявленного объекта авторами статьи выполнена оценка его морфометрических характеристик [23], представленных на рис. 14, таких как ширина пояса руслоформирования ( В ), длина излучины ( С ), радиус кривизны ( R ). В данном примере предполагаемая средняя мощность русловых отложений, рассчитанная по зависимости Collinson (1987), прогнозируется равной 14,6 ± 3 м. В табл. 2 представлены измеренные и рассчитанные параметры геометрии палеорусла.

Выводы

Предложенная авторами статья является обзорной и посвящена направлениям улучшения сейсмического изображения на этапе интерпретации сейсмических данных. Авторы проанализировали разнообразные подходы и их возможности, сосредоточив свое внимание на интерпретации таких седиментационных объектов, как палеоканалы. В первую очередь, получение сейсмического изображения подобных геологических событий зависит от разрешающей способности сейсмических исследований. Анализ вертикальной и горизонтальной разрешающей способности позволяет сделать вывод, что качественное сейсмическое изображение во многом зависит от частотных характеристик волнового поля. Примеры синтетического моделирования позволяют определиться с оптимальными значениями.

На этапе интерпретации сейсмических данных работа с частотными характеристиками волнового поля осуществляется интерпретатором через расчет соответствующих частотно-зависимых атрибутов и декомпозицию волнового поля по частотам. Одним из наиболее информативных подходов в настоящий момент является спектральная декомпозиция с синхронной визуализацией, как правило, трех наиболее информативных амплитудных слайсов, полученных в разных полосах частотного диапазона при помощи аддитивной цветовой модели RGB.

Интересным направлением интерпретации представляется графическая «дообработка» изображений, получаемых в результате динамической интерпретации. Развитие этого направления, возможно, в будущем позволит решить задачу автоматизации процесса выделения палеоканалов, что позволит снизить неопределенность и влияние фактора субъективности.

На практическом примере представлен комплексный подход интерпретации сейсмических данных для изучения палеорусловых систем тюменской свиты. В процессе работы для целевого интервала выполнен атрибутный анализ, спектральная декомпозиция, кластеризация, применен подход, реализованный в технологии eXchroma. Оценка информативности перечис-

ГЕОФИЗИЧЕСКИЕ ИССЛЕДОВАНИЯ

Табл. 2. Параметры морфологии палеорусла

Tab. 2. Parameters of paleo riverbed morphology

Параметры Значения, вычисленные по площади исследования Ширина пояса руслоформирования (В), м 4000 Ширина русла (W), м 450 Длина палеорусла, км 47 Длина долины палеорусла, км 25 Коэффициент извилистости 1,88 Длина излучины (С), м От 7000 до 10 000 Радиус кривизны (R), м От 1500 до 2500 Вычисленная средняя мощность в пределах пояса меандрирования (h), м 14,6 ± 3 ленных подходов осуществлялась на экспертном уровне. Применение вышеперечисленных подходов позволило закартировать в пределах целевого интервала несколько палеорусел и спрогнозировать для одного из них морфометрические характеристики.