Универсальный способ восстановления резервируемых данных с оптимизацией по скорости выполнения

Важность проблемы сохранности данных обусловлена принципиальной неустранимостью возможности их утраты. Наиболее распространенным способом повышения безопасности данных является периодическое создание резервных копий (далее РК).

Процесс восстановления данных сводится к объединению последовательности созданных резервных копий, называемой путем восстановления. Одной из основных характеристик процесса восстановления является скорость его выполнения. При автоматизированном восстановлении производится специализированная процедурадля каждого алгоритма резервного копирования. Для традиционно используемых алгоритмов, вопрос поиска пути восстановления данных не стоит. Так, при работе инкрементной схемы создается единственная цепочка копий, и при восстановлении к состоянию на любой момент резервирования существует лишь единственный путь. Путь восстановления для полного резервирования редуцируется в единственную полную копию данных на момент времени восстановления. Однако создание дополнительных избыточных копий по требованию пользователя, а также возможность утраты некоторой части резервных данных образуют отклонения от работы алгоритмов резервного копирования,поэтомуприменениеспециализи-рованных процедур восстановления значительно усложняется [1]. В таких случаях возможно, что выбранный системой путь восстановления не будет являться наилучшим по скорости. Возможно также, что система не сможет найти путь и управление будет передано пользователю. При работе более сложных алгоритмов создания резервных копий также появляется возможность восстанов- ления данных по нескольким путям [2]. Таким образом, в общем случае может существовать несколько различных путей, с различной скоростью восстановления, что обуславливает проблему выбора оптимального среди них.

Появляется необходимость в универсальном адаптивном способе, учитывающим возможности утраты резервных данных и дополнительного создания копий, подходящим не только для восстановления данных при работе алгоритмов резервного копирования, но для любого набора копий вообще. Требуется также возможность оптимизации поиска пути восстановления по времени выполнения. Существование унифицированной процедуры восстановления позволило бы отказаться от разработки специализированных процедур для каждого реализованного алгоритма резервирования.

Постановка задачи

Для совершенствования процесса восстановления данных в указанном направлении, необходим аппарат математического моделирования работы систем резервного копирования (далее СРК). В зарубежных источниках, посвященных резервному копированию (A. L. Chervenak, V. Vellanki, Z. Kurmas, V. Gupta, A. Costello, C. Umans, F. Wu, S. Romig, L. P. Cox), повсеместно используется словесно-графический способ описания работы алгоритмов, процессов резервирования и восстановления данных. Для исследования применяется эмпирический подход, то есть алгоритмы резервирования реализуются в составе некоторой системы, где их качества тестируются на выбранных данных. Средства компьютерного моделирования необходимо дополнять построением математических моделей. Существующие узкоспециализированные способы формализации (X. W ei, W. Min, А. Ю. Телешев) не подходят для решения поставленных задач. Требуется разработка модели процесса восстановления данных в системах резервного копирования. Необходимо выделить факторы, влияющие на скорость восстановления и учитывать их при выборе пути восстановления данных.

Моделирование процесса восстановления данных

Рассмотрим систему резервного копирования, которая создает копии данных в последовательные запланированные моменты времени {tk}, где k         . Систему данных для резер вного копирования на момент времени tj ∈ tk обозначим Dj. Будем отныне всегда предполагать, что начальное (момент t0) состояние данных D0 – пустое, а D1 нет, то есть D0 = Ø, D1 ≠ Ø. Каждая сделанная копия данных сохраняется в некотором хранилище данных (репозитории). Каждую такую копию будем называть элементом репозитория. Элемент репозитория, который содержит изменения между состояниями данных с момента ts до момента ts + n , то есть от Ds до Ds + n , обозначим Rsn или R(s, n), где s и n – целые, причем n > 0, s ≥ 0. Учитывая, что начальное состояние данных пустое, R0n фактически означает полную резервную копию состояния данных в момент tn, то есть копию Dn. Множество всех элементов репозитория будем обозначать как Rep.

Сущность алгоритма РК заключается в выборе способа создания копий данных, то есть алгоритм определяет, какая часть данных должна быть скопирована на каждый момент РК.

С помощью предложенной математической схемы описания процессов резервирования данных алгоритм может быть описан функцией выхода R_scheme ( t_j ) ^⊂ 2 ^Rep, задающей соответствие каждому моменту резервного копирования t_j множества генерируемых в СРК элементов репозитория. Алгоритм также можетбыть описан функцией Rscheme (tT ) ^{c 2} Rep , задающей соответствие каждому моменту резервного копирования t_j множества хранимых в СРК элементов репозитория [3].

Имеет смысл операция объединения элементов репозитория [4]. Например, объединяя полную резервную копию системы данных на момент t_s , то есть R ₀ ^s , с элементом репозитория, содержащим изменения между состояниями данных c момента времени t_s до момента t_{s + n} , то есть c R _s ⁿ , мы получаем полную резервную копию s+n системы данных на момент t s ₊ n , то есть R0 . Следует заметить, что не все элементы могут быть объединены друг с другом. Нет смысла, например, объединять элементы, содержащие изменения данных в непоследовательные периоды времени. Для объединения несочетаемых элементов репозитория введем элемент XRep , который будет обозначать некий «испорченный» элемент.

Множество всех элементов репозитория обозначим Rep . Rep включает все возможные элементы репозитория и «испорченный» элемент XRep :

^ReP = ^{{ X} ; R i ^} i= 0,1,2...; j = 1,2,3... =

123  123

= {AKep; R 0 ; ^R 0 ; ^R 0 . . r Kr ; К^_ ; Ky ... Kj^^ К ^K^ ...) .

Операцию объединения элементов репозитория ⊕ на множестве всех элементов репозитория Rep введем следующим образом:

XRep © XRep = XRep ;

R n © XRep = XRep © R n = XRep ;

R inn e r ⁿ/ =

R1+nj, (i < j) л (j = i + n); _ XRep.

Введенная операция объединения элементов репозитория является алгебраической бинарной ассоциативной операцией, а множество всех элементов репозитория с операцией объединения элементов репозитория, то есть Rep ⊕ , является полугруппой. Проверим заявленное утверждение.

Ассоциативность операции объединения соответствует возможности непоследовательного ее применения при объединении элементов в пути. Фактически это означает возможность разбить путь восстановления на составные подпути и оперировать с ними отдельно.

Дадим формализованное определение понятия пути восстановления.

Путем восстановления данных к состоянию на момент t_k называется конечная последовательность n элементов репозитория P={R i G Rep}_{i = x} ,„_n , для которой результат последовательного применения операции объединения равен R (0, k ), то есть R i © R 2 © © R n = R(0, k ).

Длиной пути будем называть количество элементов репозитория в пути.

Система резервного копирования, в которой были произведены операции РК в моменты времени { t_k }, где k = 0; 1; 2 … T , может произвести восстановление данных к состоянию на момент t_j , если в репозитории существуют элементы, образующие путь к состоянию данных на момент РК t .

j

Процесс восстановления заключается в выборе последовательности элементов репозитория и последующем их объединении. Для построения структурной модели процесса восстановления обратимся к разделу теоретической кибернетики – теории автоматов.

Представим процесс восстановления системы данных к некоторому моменту tk в виде дискрет- нодетерминированной модели конечного автомата Мили (finite automata):

F = ,

где x GXи z, z0 GZ [5].

Тактами функционирования дискретного автомата будут являться моменты подачи на вход каждого нового элемента из последовательности элементов репозитория, образующих путь.

Множество входных сигналов (входной алфавит) X , множество выходных сигналов (выходной алфавит) Y , множество внутренних состояний (внутренний алфавит, или алфавит состояний) Z , начальное состояние z ₀, z ₀ ∈ Z , функцию переходов ф ( z , x ) и функцию выходов ф ( z , x ) определим следующим образом:

X = R scheme Ok ) ^ Rep ^- все имеющиеся элементы репозитория для некоторого алгоритма «scheme» на момент восстановления;

Y = {–1, 0, 1} – выходной сигнал, представляет собой статус произведенной операции. При этом обозначим: «–1» – результат неудачного применения элемента репозитория, подаваемого на вход, то есть результат равен XRep ; «0» – результат удачного применения, то есть результат не равен XRep ; «1» – достижение целевого состояния автомата, что означает завершение работы процедуры восстановления, то есть в результате получен R (0, k );

Z = { D t = R( 0 , t) e Rep } t = i; 2 ... k - копии данных на моменты D_t , при этом целевым состоянием является D_k ; z ₀ = R (0,1) – начальное состояние, равное имеющейся на момент восстановления полной резервной копии, как правило, это R (0,1); Ф ( R 0 e Z , R ^ е X ) - фактически означает переход в новое состояние, если объединение элементов репозитория не является «испорченным состоянием» и не «дальше» требуемого состояния: то есть ( n+h ) <  k для получаемого R ₀ ^n+h ; Ф( R 0 n g Z , R ^ g X ) - функция результата перехода, определяемая выражением (2).

Полученный конечный автомат Мили первого рода может быть представлен в виде матрицы соединений или в виде графа, отражающего схему связей элементов репозитория для процедуры восстановления.

При представлении автомата в виде матрицы соединений строки соответствуют исходным состояниям, а столбцы – состояниям перехода. Элемент A_ij = x_k/y_s , стоящий на пересечении i -ой стоки и j -го столбца, в случае автомата Мили соответствует входному сигналу x _k, вызывающему переход из состояния z_i в состояние z_j , и выходному сигналу y_s , выдаваемому при переходе.

Граф автомата представляет собой набор вершин, соответствующих различным состояниям автомата и соединяющих вершины его дуг, соответствующих тем или иным переходам автомата. Если входной сигнал x_k вызывает переход из состояния z_i в состояние z_j , то на графе автомата дуга, соединяющая вершину z_i с вершиной z_j , обозначается x_k . Для того чтобы отобразить (задать) функцию выходов, дуги графа необходимо отметить соответствующими выходными сигналами. Маркировка дуг в данном случае может быть представлена как x_k / y_s .

Рассмотрим для примера задание одного простого автомата A в матричном виде:

D 1 D 2    D 3    D 4    D 5

D 1

R ₁ ¹ /0 R ₂ ¹ /0

D 2

A=_{D 3}

R ₃ ¹ /0 R ₄ ¹ /1

-

R ₃ ² /1    -

D 4

D 5

Представление в виде ориентированного графа показано на рис. 1, при этом отображены только некоторые переходы с неудачными исходами ( y = –1), которые не меняют состояния. Для примера приведены таковые только для D и D ₅. В дальнейшем опустим маркировку исходов на рисунках графов, так как она прослеживается умозрительно. Не будем также изображать петли переходов с неудачными исходами.

Представление работы процедуры восстановления в виде ориентированного графа конечного автомата Мили удобно для дальнейшего ее исследования на предмет поиска путей восстановления, оптимальных по скорости. Нетрудно заметить, что при данной модельной интерпретации в виде вершин отображены состояния

ϕ(R0n ∈Z,Rmh ∈X)=

⎨⎧R0n⊕Rmh, (R0n ⊕ Rmh ≠XRep)∧(n+h≤k);

R0n.

' 1, (R0n © Rmm ^ XRep) a (n + h = k);

ф ( R 0 g Z , R m _m g X) = ^ 0, (R ₀ ⁿ © R m _m Ф XRep) a ( n + h <  k );

- 1, (R ₀ ⁿ © R m _m = XRep) v ( n + h >  k ).

данных, а в виде дуг – элементы репозитория, хранящие данные об изменении между двумя их состояниями. При этом номера вершинам присвоены последовательно в соответствии с моментами резервного копирования t_k . Так, началом дуги, изображающей элемент репозитория R ( l, m ), является вершина, соответствующая D_l , а концом – соответствующая D_l+m .

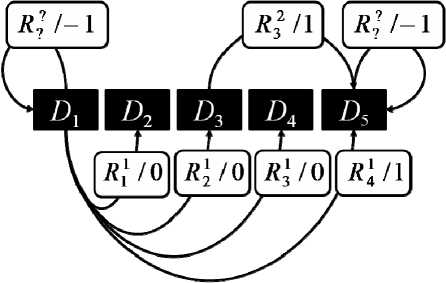
Рис. 1. Граф переходов состояний

Понятие пути восстановления в такой интерпретации становится наглядным и совпадает с понятием пути в орграфах. При этом возможно применение аппарата теории графов для отыскания кратчайших путей и путей, соответствующих некоторым наперед заданным условиям.

Факторы, влияющие на скорость операции восстановления

При отыскании оптимального пути восстановления может учитываться ряд факторов, влияющих на скорость восстановления. Объем данных для восстановления – основной фактор для решений на основе переносных носителей с последовательным доступом (магнитные ленты), так как за счет разных уровней избыточности в путях скорость восстановления может существенно отличаться.

Количество элементов репозитория в пути и объемы файловых индексов влияют на количество логических операций сравнения и объединения, что особенно важно в условиях хранилищ с произвольным доступом.

Значимость факторов может значительно отличаться в зависимости от реализации системы, при этом могут существовать дополнительные факторы. Переход к единому показателю практически невозможен, поэтому при поиске пути восстановления следует выделять наиболее значимые факторы и устанавливать для них приоритет. Далее производить поиск ряда оптимальных путей по первичному фактору, и при необходимости вести дополнительную оптимизацию по дополнительному фактору, имеющему наибольший вес в конкретном случае реализации системы.

В случае, когда данные всех элементов репозитория равнодоступны (например, если хранятся на жестком диске), процесс копирования будет занимать одинаковое количество времени для любого корректного пути, так как в любом случае будет скопировано одинаковое количество файлов.Разница во времени работы процесса восстановления будет обусловлена вычислительной скоростью алгоритмов поиска пути восстановления и скоростью работы операции определения места нахождения нужных версий файлов, зависящей от факторов длины пути и объема файловых индексов резервных данных.

Для иллюстрации важности учета обоих фак-торов,рассмотримследующийпример.Начальное состояние данных D ₀ пустое. D ₁ включает только некоторый файл A , то есть D ₁ = { A } и R (0, 1) = { A }. Далее этот файл изменяется и D ₂ = { B }, создается элемент репозитория R (0, 2), содержащий изменение данных от D ₀ до D ₂ состоящее из B . Далее процесс продолжается так, как отображено на рис. 2. Причем A^— в элементе R (1, 2) означает данные об удалении A . В результате для восстановления к моменту времени t ₃ имеются два пути: P 1 = { R (0,1); R (1,2)} и P ₂³= { R (0,2); R (2,1)}. Оба пути состоят из двух элементов репозитория каждый. Однако для объединения элементов репозитория для P₁ требуется проанализировать больше на { A } данных, чем для P₂ . Если предположить что { A } является не файлом, а совокупностью из нескольких тысяч файлов, то отличие времени работы процедуры восстановления для рассматриваемых путей может оказаться значительным.

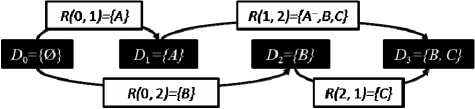
Рис. 2. Пример влияния фактора объема элементов репозитория в пути

Поэтому, при поиске оптимального пути нужно учитывать не только фактор количества элементов репозитория входящих в путь, но и их суммарный объем.

Выбор и применение алгоритмов поиска кратчайших путей

Требуется найти кратчайший путь, обладающий дополнительным свойством. Данную задачу можно рассматривать как задачу с некоторыми дополнительными ограничениями или как многоцелевую задачу, в которой учитывается не только длина, но и свойство объема файлов в элементах репозитория. Эти усложнения будут, вообще говоря, сильно увеличивать вычислительную работу, и с практической точки зрения более просто найти кратчайшие пути с минимальной длиной и выбрать среди них тот, который обладает нужным свойством.

Вообще говоря, необходимо получать простые цепи, так как наличие циклов в пути означает непригодность для восстановления.

Существует много алгоритмов, в которых заложено требование получения простых цепей, однако, как показывают исследования, это требование значительно осложняет работу алгоритма, что влечет за собой значительное увеличение времени работы алгоритма.

Следует заметить, что, как правило, для алгоритмов резервного копирования нет возможности получить цикл в пути восстановления, однако в принципе это не исключено. Ведь существует принципиальная возможность создавать элементы репозитория хранящие изменения по отношению к предыдущему состоянию данных как, к примеру, в обратной инкрементной схеме (англ. reverse incremental). Нужно иметь в виду такую возможность и в действительно универсальном алгоритме восстановления это нужно учитывать.

Можно было бы создать процедуру восстановления с использованием алгоритмов, исключающих циклы для тех схем резервного копирования, где наличие таких путей не исключено и другой алгоритм в противном случае. Но чтобы добиться действительной универсальности процедуры нахождения пути необходимо избавиться от требования излишних пользовательских параметров.

В таком случае имеет смысл использовать гибридные алгоритмы. При работе такого алгоритма, при поиске каждого последующего оптимального пути, изначально работает алгоритм, который не исключает появление циклов, найденный путь проверяется, и в случае обнаружения цикла, оптимальный путь находиться с использованием другого алгоритма, гарантирующего получение простого пути.

Оптимальность выбора гибридного алгоритма поиска K кратчайших путей как основы алгоритма поиска оптимального пути восстановления подтверждается исследованиями [6], проведенных на различных классах графов. По данным исследований гибридный алгоритм в составе с алгоритмом Йена превосходит по скорости поиска другие алгоритмы поиска простых путей, в том числе алгоритм Перко (Perko), алгоритм Йена в оригинале и модифицированный, алгоритм Мартинса и Паскоаля (Martins & Pascoal).

Таким образом, применение гибридного алгоритма отлично подходит для поиска оптимального пути восстановления в системах резервного копирования.

Для поиска путей с требованием минимизации по одному фактору будем использовать алгоритм Дейкстры.

В результате при работе процедуры построения пути восстановления будут работать три алгоритма теории графов: гибридный алгоритм, алгоритм Йена и алгоритм Дейкстры.

Алгоритм Дейкстры строит кратчайший (s, t) G(N, A) за время O(n2), где N – множество вершин, а А этом n = |N| – количество вершин, а m = |A| – количество дуг.

При реализации алгоритма в случае поиска пути восстановления необходимо учесть возможность множественных дуг между двумя вершинами. Поэтому при проверке вершин с временными метками следует рассматривать все возможные варианты дуг. При построении непосредственно пути надо учитывать не только последовательность прохождения вершин, но и использованные при этом дуги.

Удобно связывать с каждой вершиной v еще один список меток 0 ( v ) , в который следует заносить идентификатор указывающей на v дуги в ( )-пути, имеющем минимальный вес среди всех ( s, v )-путей, проходящих через вершины, получившие к данному моменту постоянные метки. Таких путей может быть несколько, поэтому 0 ( v ) в общем случае является списком, однако если требуется только один путь, то список следует понимать как просто метку. После того как вершина t получила свою постоянную метку, с помощью меток Θ можно легко указать последовательность вершин и дуг, составляющих кратчайший ( s, t )-путь.

Заметим, что для работы алгоритма Йена вкупе с алгоритмом Дейкстры для верной работы не требовалось бы указания всех возможных дуг в кратчайшем пути в работе алгоритма Дейкстры, потому что алгоритм Йена, перед тем как запускать каждый раз алгоритм Дейкстры, удаляет уже просмотренные дуги и рассматривает оставшиеся. Таким образом, нет возможности пропустить нужный путь. Для гибридного алгоритма ситуация сходная. Идеально для задачи подходит представление мультиграфа списками смежности. Так как требуется найти путь, кратчайший в смысле количества использованных элементов репозитория, следует считать все веса равными единице.

При поиске кратчайших путей по алгоритму Йена [8], работу алгоритма следует останавливать, как только следующий найденный путь будет обладать большей длиной, чем уже найденные. Затем из найденных путей следует выбрать оптимальный по второму фактору. Для этого достаточно найти путь с минимальным суммарным объемом входящих в него элементов репозитория. Так, каждой дуге (x, y) ∈ A поставлен в соответствие вес c е IR. Pk = {s,vk,vk,...,vk ,t} - k-ый xy                     , 2 , 3 ,, qk , кратчайший (s, t)-путь, где vi – его вершины. Пусть Pik – отклонение от пути Pik-1 в точке i. Под этим понимается следующее: Pik – кратчайший из путей, совпадающий с Pik-1 от s до i-ой вершины, а затем идущий к (i + 1)-ой вершине по дуге, отличной от дуг к (i + 1)-ой вершине тех (ранее уже построенных) кратчайших путей Pj (j =1; 2… k –1), которые имеют те же самые начальные подпути от s к i-ой вершине, что и Pk-1. Pkприходит в вершину t по кратчайшему подпути, не проходящему ни через одну из вершин {s, vk-1,vk-1,...,vk—1} , участвующих в формировании первой части пути Pik. Алгоритм начинает работу с нахождения кратчайшего пути P1 c помощью алгоритма Дейкстры. Далее находят следующий оптимальный путь Pk, k = 2. Для этого подбирают лучшие отклонения от заданного пути, используя на каждом шаге алгоритм Дейкстры. Кратчайший среди найденных кандидатов pk и будет являться Pk. Далее переходят к поиску Pk, для k = 3. И так далее. Временная сложность алгоритма O(Kn3) с учетом того, что используется алгоритм Дейкстры с неотрицательными весами.

При работе гибридного алгоритма [6], кратчайший ( s, t )-путь, который отклоняется от P^k на вершине v k , то есть p ^k , ищется в виде Root_P k ( s , v k ) ° ( v k , j ) ° T ( j ) , так, что дуга ⁽ v k . ^{j )} не принадлежит никакому из кандидатов P^j , найденных до этого. Здесь Root р ( s, v k ) - подпуть P^k от s до v k ; операция объединения путей p и q обозначена как Р ° q , при этом объединенный путь образован p и следующим за ним q .

Создание каждого нового кандидата таким способом более эффективно, так как процеду- ра отыскания кратчайшего пути на каждом этапе сводится к проблеме выбора нужной дуги (vik, j), что может быть сделано за время O(1), в отличие от применения алгоритма Дейкстры, который в нашем случае с неотрицательными весами выполняется за время O(n2). Однако такой алгоритм может вернуть путь с циклами, когда RootPk (s, vk) и Tt(j) содержат одинаковые узлы. В таком случае гибридный алгоритм переключается на использование алгоритма Йена. В худшем случае время работы гибридного алгоритма будет идентично алгоритму Йена, то есть O(Kn3), в лучшем же случае, когда в отклонениях циклов не будет, следует ожидать Ω(Kn + n2 + mlog n).

При практической реализации для тривиальных случаев работы схем РК, когда проблемы множественности путей не стоит и существует лишь единственный путь, процедура гибридного алгоритма может быть отключена и выполнение сводится к алгоритму Дейкстры, что максимизирует производительность.

Способ восстановления данных

Общая процедура восстановления может быть описана следующей последовательностью действий:

• 1.    Определить наиболее значимые факторы, влияющие на скорость восстановления, основываясь на особенностях реализации системы резервного копирования и типе использованных носителей.

• 2.    При создании каждого нового элемента репозитория сохранить метаданные, включающие файловые индексы.

• 3.    Произвести проверку корректности элементов репозитория, идентифицировать их доступность.

• 4.    Построить граф репозитория для автомата процесса восстановления данных к искомому состоянию.

• 5.    Произвести поиск кратчайших путей на графе репозитория сучетом выбранныхфакторов.Вслучае, если пути восстановления не существует,следует:

• 6.    Произвести восстановление данных по найденному пути.

• 7.    Проверить результат восстановления данных, используя хэш или другую информацию о целевом состоянии данных. В случае неудачного результата следует перейти к этапу 3. В случае, когда при втором проходе найден идентичный путь и восстановление невозможно следует прервать процедуру восстановления с ошибкой.

Способ поиска оптимального пути для восстановления данных был реализован в составе раз- работанной СРК, на базе которой проведен ряд испытаний на различных алгоритмах РК, среди которых полное, инкрементное, дифференциальное, мультиуровневое копирования, схема Костелло, Z Scheme, а также некоторые другие. Опыт эксплуатации показал применимость предложенного способа.

Заключение

В работе решена задача построения универсального способа поиска оптимального пути восстановления данных, пригодного для реализации автоматизированного восстановления при работе с любым набором элементарных копий в репозитории и не зависящего от используемого алгоритма РК. Для этого была формализована операция объединения элементов репозитория. Процедура восстановления сводится к объединению нужного множества элементарных копий в определенной последовательности. Процесс восстановления представляется конечным автоматом.

Произведен анализ возможных факторов, влияющих на оптимальность скорости восстановления по найденному пути. Ввиду практической невозможности построения агрегированного показателя в общем случае предлагается выделение таковых при реализации системы. Способ отыскания пути остается прежним в каждом случае, в чем и заключается его универсальность.

Для поиска путей, оптимальных по некоторым факторам применяется аппарат теории графов. Было осуществлено исследование современных методов отыскания кратчайших путей, в результате которого выявлена оптимальность применения гибридного алгоритма в составе с алгоритмом Йена для решения задачи отыскания оптимального пути восстановления в СРК.