Управление движением спутника-инспектора вблизи Международной космической станции

Международная космическая станция (МКС) является одним из крупнейших объектов человеческой техники в космосе, который требует регулярного технического обслуживания для эффективного и безопасного функционирования. Важное значение имеет обслуживание станции в открытом космосе. К числу работ за пределами МКС относятся, например, систематические обследования и ремонт солнечных батарей, обеспечивающих МКС электроэнергией; постоянный осмотр обшивки станции с целью поиска утечек воздуха или других повреждений, которые могут представлять угрозу для безопасности экипажа ; установка нового оборудования или сборка станции.

В настоящее время внешнее техническое обслуживание МКС осуществляют астронавты, используя скафандры и специализированное оборудование. Ввиду возможных поломок оборудования астронавта, потери контроля над движением, утечки кислорода или даже столкновения с космическим мусором, угроза для жизни человека при выходе в открытый космос очень высока.

В истории космонавтики такие ситуации уже случались. Например, 16 июля 2013 года выход К. Кэссиди и Л. Пармитано в открытый космос с борта МКС был внезапно прерван из-за утечки воды в скафандре европейца. Возникла угроза жизни и здоровью космонавта: образовался пузырь воды внушительных размеров , от которого Пармитано мог захлебнуться. Во время выхода в космос астронавты должны были проложить дополнительные кабели связи на внешней поверхности станции для работы нового российского Многофункционального лабораторного модуля . Те запланированные работы, которые не были выполнены во время упомянутой миссии, пришлось перенести на будущие выходы в открытый космос согласно расписанию [1, 2].

Из числа последних происшествий стоит упомянуть инцидент, произошедший 24 июня 2024 года, когда у астронавта NASA Трейси Дайсон из скафандра хлынула вода в открытое космическое пространство и стала мгновенно замерзать. Утечку быстро устранили, а астронавтов вернули на МКС. Однако им не удалось выполнить поставленные задачи [1].

Чтобы минимизировать существующие риски, для решения некоторых сервисных задач предлагается использовать спутник-инспектор (СИ) — малый космический аппарат, предназначенный для проверки и контроля состояния других космических объектов. Он обладает функциями наблюдения, фиксации и передачи данных, а также способностью проведения бесконтактной диагностики неисправностей и длительного облета вокруг МКС для оперативного реагирования на возникающие запросы технического обслуживания станции.

Стоить упомянуть существующий российский проект «Нивелир» по созданию серии СИ, которые предназначены для наблюдения и проведения ремонтных работ других спутников на орбите Земли. Спутники данной программы располагают широким спектром возможностей, среди ко- торых, удалённое наблюдение за другим спутником или объектом на орбите, наблюдение Земли, возможность сближения и контакта с объектом на орбите, изменение орбиты, диагностика неисправностей, фотосъёмка [3].

Построение движения СИ возможно с помощью системы уравнений Клохесси-Уилтшира [4], которая описывает относительное орбитальное движение одного тела относительно другого под действием их взаимного гравитационного воздействия. Эти уравнения были разработаны У. Х. Клохесси и Р. С. Уилтширом и впервые опубликованы в 1960 году. Вывод данной математической модели приведен в предыдущей работе по исследованию сближения СИ с другим космическим аппаратом (КА) [5]. Кроме того, используя эти уравнения, была произведена оценка параметров движения с точки зрения безопасности сближения, а также определены положения для длительного наблюдения за КА.

1    Постановка задачи

Движение СИ будем рассматривать в орбитальной системе координат (ОСК) [6], начало отсчета которой свяжем с центром масс Российского сегмента (РС) МКС. ОСК определяется следующим образом: ось Ox ₀ направлена по радиус-вектору, соединяющему центр масс Земли с центром масс РС МКС; ось Oy ₀ принадлежит плоскости траектории МКС и направлена в сторону ее движения; ось Oz ₀ дополняет систему до прямоугольной правой (рис. 1).

Для предотвращения столкновения СИ с МКС необходимо определить область вокруг МКС, в которой движение спутника небезопасно, и моделировать полет таким образом, чтобы избежать попадания в «запрещенную» зону.

В Спецификации РС МКС установлены следующие требования безопасности к движению в окрестности МКС:

• 1.    Облёт МКС должен выполняться на расстоянии 160-250 метров относительно большего диаметра ближайшего модуля РС МКС.

• 2.    Причаливание к стыковочному узлу допускается внутри виртуального конуса с углом ± 10 o в вершине относительно оси стыковочного узла.

• 3.    Находясь в установленном конусе, разрешается выполнять облет МКС, выдерживая дальность в диапазоне 40-60 метров от узла стыковки.

• 4.    Перед стыковкой необходимо выйти на ось стыковочного узла и выполнить зависание, поддерживая расстояние до узла в диапазоне 30-40 метров (положение 0, рис. 1).

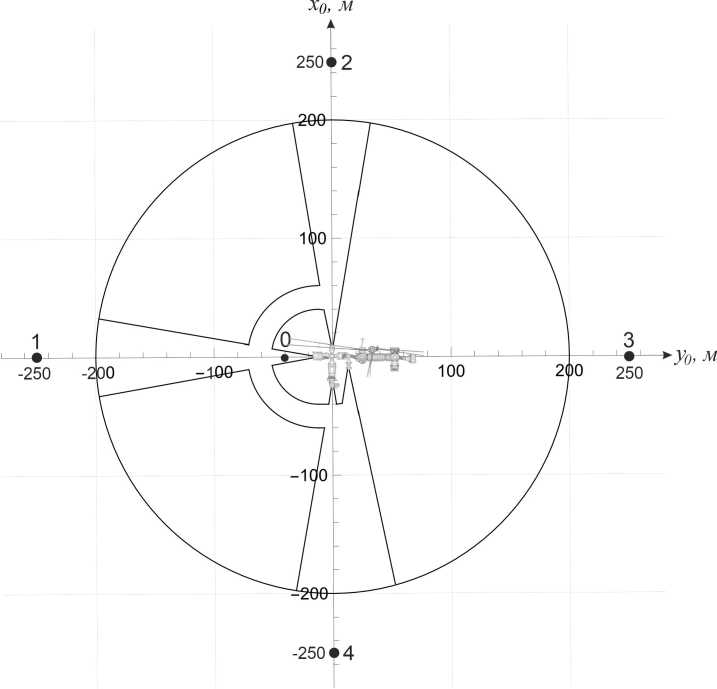
Рис. 1. Орбитальная система координат и зоны движения СИ в окрестности МКС

Пусть задачей СИ является облет вокруг МКС и выполнение зависания у узла стыковки, который обозначен положением 0 (рис. 1). Тогда с учетом поставленной задачи и перечисленных требований, определим в настоящей работе зону безопасного облета МКС для СИ за пределами окружности радиуса 200 м, проведенной из центра ОСК. Т.к. на РС МКС находятся 4 стыковочных узла, то движение СИ внутри установленной окружности разрешено в конусах с углом ± 10 ^o в вершине относительно оси каждого стыковочного узла и в полукольце, проведенном из выбранного узла стыковки (положение 0, рис. 1). Меньший радиус полукольца 40 м, а больший — 60 м (рис. 1).

Таким образом, ставится задача определения управления СИ с целью безаварийного попадания в стыковочную зону после облета МКС.

2    Математическая модель

Для построения относительного орбитального движения СИ используются вышеупомянутые уравнения Клохесси-Уилтшира:

x( t ) = 3 ш о x ( t ) + 2 ^ ₀ y ( t ),

y⁽ t ) = - 2 М 0 x ⁽ t ),                           (1)

z( t ) = -a 02 z (t ), где а0 =

GM

R

орбитальная скорость МКС, G — гравитационная по стоянная, M — масса Земли, R0 — радиус орбиты МКС.

Решив аналитически систему дифференциальных уравнений (1), получим закон пассивного движения СИ:

л      2y„ x„ .      , С x (t) = 4 x 0 +--°- +—-sin а 01 - 3 x 0 +--°- I cos a 01, a о a 0          ^

т x         2 xn (.     4 y„ ^ .         2 xn...

y ( t ) = - (6 a ₀ x ₀ + 3 y ₀ ) t + y ₀--⁰ + 6 x ₀ +---- I sin a ₀ 1 + —⁰ cos a ₀ 1 , (2)

a 0   I      a 0 J

z z (t) = —sin a 01 + z 0sin a 01, a 0

где x ₀ , y ₀ , z ₀ — начальные координаты СИ, x ₀ , y ₀ , z ₀— начальные скорости СИ, t — время полета СИ.

Закон изменения скоростей находится путем дифференцирования координат (2) по времени:

x(t) = x0 cos a01 + (3x0a0 + 2y 0 )sin a01, y (t) = -( 6a 0 x 0 + 3 y 0 ) + (6a 0 x 0 + 4 y 0) cos a 01 - 2 x 0sin a 01, (3)

z ( t ) = z ₀ cos a ₀ 1 - z ₀ a ₀ sin a ₀ 1 .

В настоящей работе для моделирования движения СИ с двигателем малой тяги (ДМТ) применяются уравнения Клохесси-Уилтшира (1), модернизированные путем добавления силы тяги двигателя:

F

x ( t ) = 3 a ₀ x ( t ) + 2 a ₀ y ( t ) + —- ,

m

F y ( t ) = - 2 a 0 . x ( t ) +      ,

m

F ^{z (} t ) = ^-a 0 ^{z (} t )⁺ —,

m где m — масса СИ, Fx — сила тяги двигателя, действующая по направлениям оси x, Fy — сила тяги двигателя, действующая по направлениям оси y.

В работе [5] процесс сближения СИ с КА моделировался на основе двухимпульсного маневра: мгновенных импульсов наведения и замедления, которые вычислялись с использованием систем уравнений (2) и (3). Данный подход является идеализированным и не учитывает длительность работы двигателя. Уравнения (4) позволяют устранить отмеченный недостаток.

В данном исследовании упомянутые импульсы производятся за счет включений двигателей, промежутки времени работы которых определяются с помощью второго закона Ньютона в импульсной форме:

m А V = F A t , (5)

где А V — импульс наведения/замедления, определенный с помощью уравнений (3).

Выразив искомую величину времени из формулы (5), получим

A t =

m А V

F

3    Моделирование движения

Полет СИ состоит из трех участков движения: первого управляемого движения, в конце которого спутник приобретает необходимую скорость для достижения конечной точки; пассивного движения; второго управляемого движения, обеспечивающего остановку СИ на заданных коорди -натах.

Моделирование первого управляемого движения начинается с вычисления импульса наведения в координатной форме. Данный процесс описан в работе [5]. Затем, используя выражение (6), определяется время работы ДМТ, по истечении которого спутник продолжает полет без управляющего воздействия. Для построения второго управляемого движения необходимо найти скорости СИ в конце участка пассивного движения. С учетом найденного импульса замедления вычисляется время работы ДМТ для торможения СИ и остановки в конечной точке. Тогда сила тяги на трех участках движения будет определяться следующими системами выражений

F_H ,0 <  t < A t_H , н_xн_x

F x =\

0, A t_H <  t <  t_K -A t₃ , н_xк з _x

F3 , tK зxк

—

A t₃

з _x

	F H у , 0 <  t <A t н у ,
F y	0, A t н у <  t <  t к -A t з у ,                    (8) F з у , t к — A t з у <  t <  t к ,

где F , FH — номинальная сила тяги двигателя, направление действия xy которой совпадает с направлением вектора импульса наведения СИ;

F3 , F3 — номинальная сила тяги двигателя, направление действия ко-xy торой противоположно вектору импульса замедления СИ; At , AtH — xy время работы ДМТ при импульсах наведения по координатам x и у со ответственно; A t3 , A t3 — время работы ДМТ при импульсах замедле-xy ния по координатам x и y соответственно, tк— конечное время полета СИ.

Таким образом, движение СИ моделируется на основе численного решения системы уравнений (4) с учетом найденных параметров работы ДМТ (7), (8).

4    Маневрирование вблизи МКС

Пусть СИ массой 50 кг находится на орбите МКС радиуса R 0 = 6780 - 10 3 м. Движение спутника будем рассматривать только в плоскости Ox ₀ y ₀ . В начальный момент времени относительное движение спутника отсутствует. СИ может начать движение из положений 1, 2, 3 или 4 (рис. 1). Тогда с учетом установленных зон безопасного движения в окрестности МКС, имеем следующие маршруты движения: 1-0, 2-1, 3-2, 4-3, 4-1.

Для математического моделирования и проведения вычислительных экспериментов было выбрано пять ДМТ с разными техническими характеристиками [7] (табл. 1).

Таблица 1

Двигатель	Номинальная сила тяги F , Н	Масса, кг	Время включения, с	Кол-во включений
МД08	0,819	0,105	0,05…100	80 000
МД5	4,9	0,35	0,012…3000	250 000
17Д58Э	13,3	0,55	0,03…10 000	450 000
РДМТ50М	54	1,3	0,03…300	100 000
11Д428А	130,5	1,5	0,03…2000	500 000

В данной работе проведен сравнительный анализ результатов моделирования движения с использованием двух ДМТ: двигателя с наименьшей номинальной силой тяги среди представленных – МД08 и наибольшей – 11Д428А. В результате построения полета СИ по уравнениям (4) его конечные координаты и скорости получились отличными от заданных, т.е. приобрели отклонения (табл. 2), которые визуально видны на рисунке 2. Эти отклонения возникли в виду того, что импульс наведения, вычисленный по уравнениям Клохесси-Уилтшира (2), предполагается мгновенным. В то время как на смоделированном участке движения СИ приобретает необходимые скорости по окончании работы двигателя (табл. 3).

Численные результаты, полученные при моделировании маршрута 4-1, рассматривать не имеет смысла, так как в данном случае СИ совершает полет с нарушением установленных зон безопасного движения вблизи МКС (рис. 2, рис. 3).

Таблица 2

Двигатель	Маршрут	Отклонение x , м	Отклонение y , м	Отклонение Vx , м/с	Отклонение Vy , м/с
МД08	1-0	11,289	42,992	0,052	0,004
	2-1	26,441	0,316	0,001	0,017
	3-2	8,226	23,642	0,003	0,005
	4-3	26,441	0,316	0,001	0,017
11Д428А	1-0	0,058	0,159	1,89 ⋅ 10 - 4	2,68 ⋅ 10 - 5
	2-1	0,172	-0,006	3,41 ⋅ 10 - 6	1,27 ⋅ 10 - 4
	3-2	0,053	0,153	2,03 ⋅ 10 - 4	2,47 ⋅ 10 - 5
	4-3	0,172	0,006	3,41 ⋅ 10 - 6	1,27 ⋅ 10 - 4

Таблица 3

Двигатель	Маршрут	tк , с	∆ tн x , с	∆ tн y , с	∆ t , с зx	∆ t , с зy
МД08	1-0	240	14,128	51,732	11,167	53,023
	2-1	600	16,858	40,966	30,654	9,034
	3-2	600	32,049	6,446	17,254	40,112
	4-3	600	16,858	40,966	30,654	9,034
	4-3-2-1-0 ( Σ )	2040	79,894	140,11	89,729	111,203
11Д428А	1-0	300	0,088	0,256	0,088	0,256
	2-1	600	0,106	0,257	0,201	0,201
	3-2	600	0,201	0,041	0,106	0,257
	4-3	600	0,106	0,257	0,201	0,201
	4-3-2-1-0 ( Σ )	2100	0,501	0,811	0,596	0,594

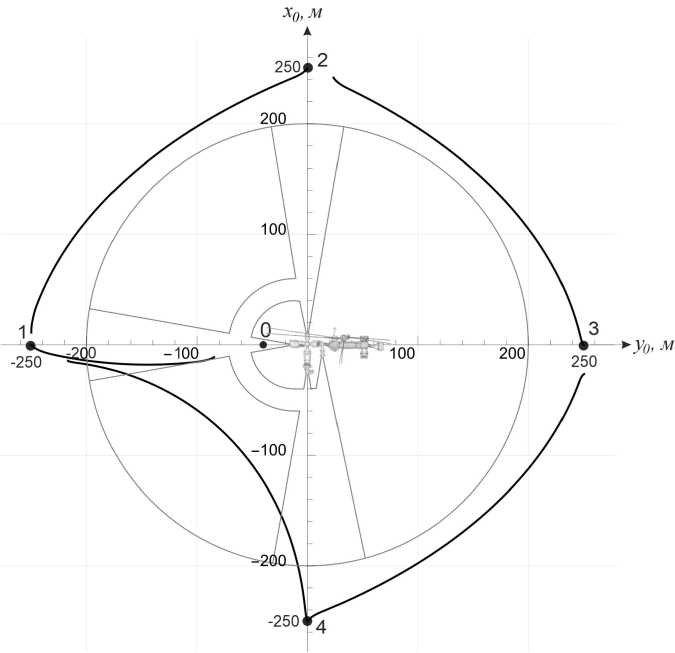
Рис. 2. Траектории движения СИ с ДМТ МД08

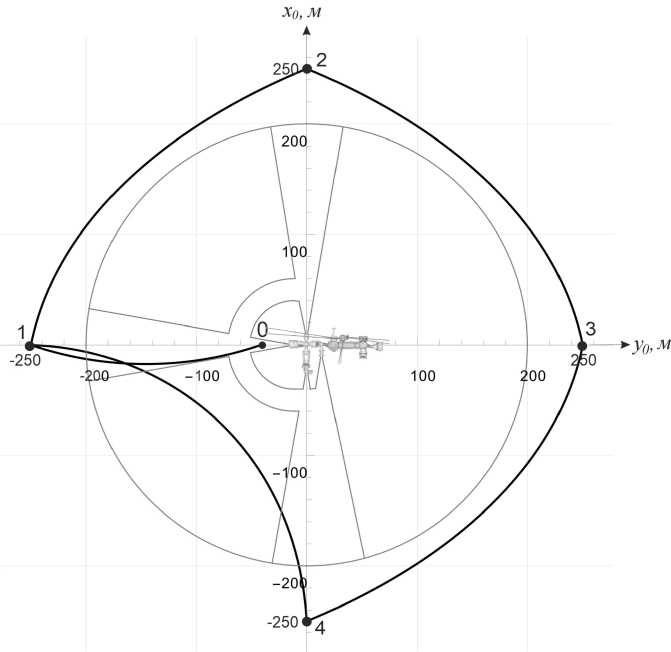
Рис. 3. Траектории движения СИ с ДМТ 11Д428А

Отклонения, полученные при моделировании движения с двигателем большей тяги близки к нулю (табл. 2). Однако масса такого двигателя в 14 раз превышает массу двигателя с наименьшей силой тяги (табл. 1), что в свою очередь значительно увеличит массу СИ, так как его конструкция в случае плоского движения предполагает наличие как минимум четырех ДМТ.

Таким образом, подбирать двигатель для СИ необходимо не только из соображений точности моделирования, но и учитывая изменение массы конструкции спутника при использовании выбранного двигателя.

Заключение

СИ может сыграть важную роль в обеспечении безопасности и эффективности работы МКС, а также для предотвращения возможных столкновений и конфликтов в космосе. Таким образом, математическое моделирование движения СИ и его исследование являются фундаментальными шагами для разрешения существующих трудностей технического обслуживания станции.

В качестве основных результатов работы следует отметить определение области безопасного маневрирования спутника вблизи МКС, построение уравнений движения СИ с ДМТ, определение параметров включения двигателей, а также сравнение использования двух ДМТ в результате математического моделирования полета спутника и проведения численных экспериментов.

Результаты работы могут быть использованы при проектировании и моделировании движения СИ или другого малого КА с двигателем малой тяги, в задачу которых входит длительный облет, сближение с другими космическими объектами, а также при расчете требуемого объема рабочего тела, при выборе двигателей и других компонентов конструируемого КА.