Управление фирмой в условиях нестабильности внешней среды

Управление фирмой в условиях нестабильности внешней среды является одной из ключевых задач современного менеджмента [1, 2]. Быстрые изменения в экономической, политической и технологической сферах создают высокую степень неопределенности, с которой сталкиваются организации. Учет нестабильности внешней среды в моделировании прибыли фирмы можно осуществить через стохастическое моделирование функции шоков [3], которое позволяет включать случайные переменные и неопределенности, отражая реальность более точно. Этот подход учитывает риски и вероятность различных исходов, что важно для принятия обоснованных решений и долгосрочного планирования, делая его наиболее эффективным способом анализа влияния внешних факторов на прибыль [4].

Цель исследования. В статье рассматривается модель управления прибылью фирмы, занимающейся розничной продажей автомобильного топлива. Особое внимание уделяется учету нестабильности факторов спроса при построении оптимизационной модели [5]. С помощью дискретной динамической стохастической модели частного (частичного) равновесия моделируются изменения цены и количества товара на рынке в течение определенного периода времени [6]. Учитываются риски и неопределенности, связанные с изменениями цены и количества товара на рынке, стратегия производства и ценообразования определяется в соответствии с этими рисками в виде интервала. На основе моделируемых данных определяется оптимальное количество товара, которое необходимо произвести для максимизации прибыли [7]. Определяется оптимальная цена товара [8], которая будет максимизировать прибыль при данном количестве товара.

Материалы и методы исследования. Теоретическая функция спроса описывает зависимость количества товара, которое потребители готовы купить, от его цены, доходов потребителей и множества других тесно связанных факторов. Используются функции спроса [5] различного вида, мы применим линейную аппроксимацию:

Р

Qd = Q - k-- max

W

l •--+ 3,

ИПЦ

Где Qd – спрос; Q – общий объём рынка; P – цена топлива; k – чувствительность к цене; l – чувствительность к доходам; W – денежные доходы населения; ИПЦ – индекс потребительских цен (основной показатель инфляции); 3 - шоки.

Динамику цен на бензин за последние 10 лет возьмем также из официальных открытых источников, оценим цену средним цен 4-х ви- дов топлива: дизель, АИ-92, АИ-95, АИ-98. Средняя цена и будет использована для вычисления эмпирической функции спроса.

Результаты и их обсуждение . Проанализировав данные за период работы фирмы с 2012 по 2022 год, можем составить эмпирическую функцию спроса, а также её прогноз на основной вид товара – бензин (рис. 1).

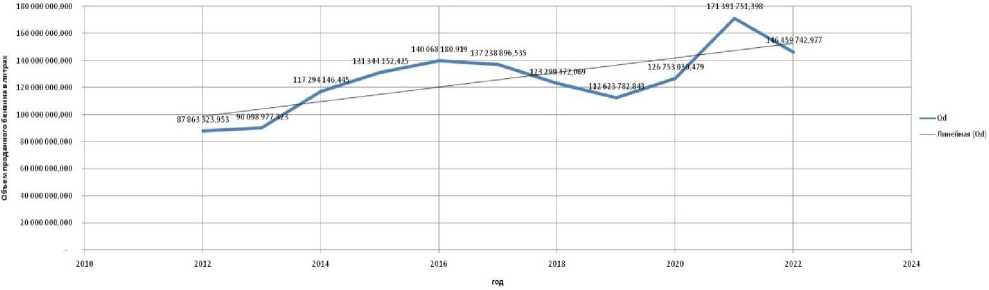
Рис. 1. Динамика спроса на бензин 2013-2022 гг. по Москве и МО

Общий объём рынка Q , чувствитель- найдём приблизительно с помощью метода ность к цене k, чувствительность к доходам l    наименьших квадратов.

Q _maх= 5 8 34 - 10⁵; k = 48 - 10⁵; l = 34 - 10⁵

Отклонение прогноза от реальной функции спроса будем считать влиянием шоков – эти события можно рассматривать, как нестабильность внешней среды. Подставив найденные коэффициенты в прогнозируемую модель, построим её график и наложим его на эмпирическую функцию спроса.

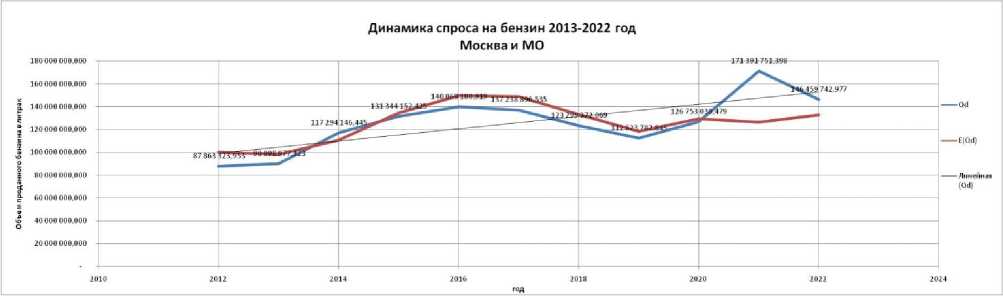
Рис. 2. Динамика спроса на бензин 2013-2022 гг. в Москве и МО

Шоки, с поправкой на инфляцию, можно выразить следующим образом:

s = E (Qd)- Qd

ИПЦ

Резкий рост прибыли в 2021 году почти на 35% привел к смещению среднего значения шоков, исключим это значение, чтобы полу- чить более объективный результат. На рисун ке 3 представлен график шоков.

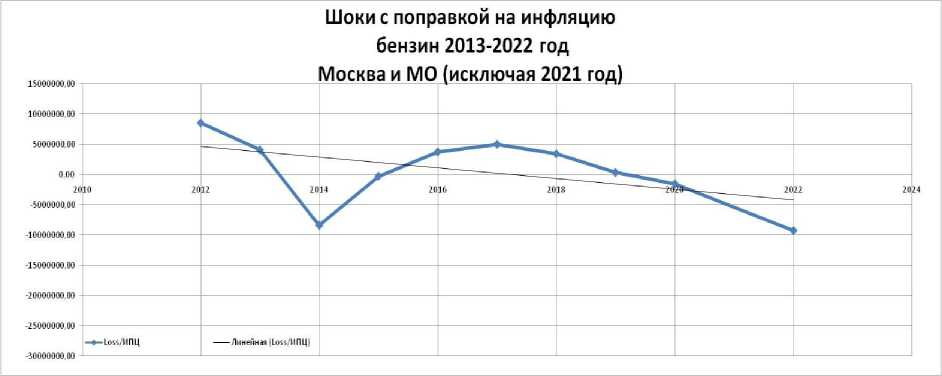
Рис. 3. График шоков на рынке бензина 2013-2022 г. Москва и МО

Форма функции Qs , описывающей зависимость между предложением и ценой, может варьироваться в зависимости от рыночной структуры, в которой действует предприятие. В случае монополии, где только одно пред- где q – количество товара, производимого монополистом.

Дискретная динамическая стохастическая модель частного (частичного) равновесия,

Данное уравнение отражает баланс между ценой товара и другими факторами, влияющими на спрос и предложение, и свидетельствует о том, что они находятся в равновесии. В случае изменения любого из этих факторов, равновесие может быть нарушено, что приведет к колебаниям цены товара до тех пор, пока не будет достигнуто новое равновесие.

приятие контролирует рынок (в т.ч. географической монополии, при которой точки продаж разных фирм достаточно удалены друг от друга, чтобы избегать конкуренции), функция Qs может быть представлена как

Qs = q ,                                   (4)

описывающая изменения количества товара на рынке в условиях неопределенности:

Qd = Qs , (5)

Функция выручки представляет собой математическую модель, которая показывает, какую выручку получает фирма от продажи определенного количества товара или услуг при заданных ценах. В простейшем случае функция выручки может быть представлена следующим уравнением:

TV = Qd ■ P ,                                 (6)

где P – цена товара или услуги; Функция   чества товара или услуг, и может быть описа- издержек показывает, какие затраты несет   на следующим уравнением фирма при производстве определенного коли-

TC = VC + FC,

где TC (q) - общие издержки фирмы при производстве товара или услуг в количестве q; FC – постоянные издержки (fixedcosts), которые не зависят от объема производства и включают в себя затраты на аренду помещений, оплату труда административного персонала, амортизацию и прочее; VC – перемен- ные издержки (variablecosts), которые зависят от объема производства и включают в себя затраты на сырье, материалы, энергоносители и т.д.

Функцию прибыли опишем как разность функции выручки и функции издержек:

П = TV - TC ,                             (8)

С учётом выражений (1) и (2) функцию выручки можно записать в следующем виде:

TV =

ИПЦ

48 - 10 5

- Qd + 5834 - 10 5

- 34 - 10⁵

W

ИПЦ

^

+ 8 Qd,

TC = 339 - 10 ^{- 10} Qd ² + 8.133 Qd + 15178 - 10⁵ + FC ,              (10)

Прогноз на прибыль в следующем периоде ности 98%, который будет определятся дове-найдём в виде доверительного интервала рительным интервалом для шоков.

П ( Qd H П ^ ; П right ] , с уровнем доверен-

П ( Qd ) =

ИПЦ

48 - 10⁵

- Qd

+ 5 8 34 - 10⁵ - 34 - 10⁵

W

ИПЦ

+ 8 Qd -

- ( 339 - 10 ^{- 10} ) Qd ² - 8.133 Qd - 15178 - 10⁵ - FC ,

С учётом доверительного интервала для шоков получим

П1е/;=-2391-10"10 -q2 + 39.914-q-15178-105, nief. = -2391 -10-10 - q2 + 44.283 - q -15178 -105,                  (12)

Если считать, что производитель всегда стремится получить наибольшую прибыль, то задачу максимизации прибыли можно концептуально описать следующим образом: требуется определить такую технологию (т.е. такие объемы затрат ресурсов), которые приносят максимальную прибыль. На самом деле, это может быть справедливо только для фирм, которые находятся в единоличном владении; если же у фирмы несколько собственников, то совершенно не обязательно, чтобы собственники ставили менеджерам задачу максимиза- ции прибыли – скорее они захотят максимизировать не прибыль, а стоимость фирмы. Кроме того, на выбор объема производства могут влиять стратегические соображения и ограничения на отдельные факторы производства.

Решая задачу максимизации прибыли, было получено оптимальное значение чистой прибыли в 2023 году П* e[1477 -105;5323 -105], которое достигается при соответствующем оптимальном объёме производства, заключенном в диапа- зоне q* ∈ [834 ⋅ 105;925 ⋅ 105] , в то время как диапазон безубыточности функции прибыли q ∈ [586 ⋅ 105;1083 ⋅ 105] , минимальная пороговая цена одного литра топлива – 54.84.

Фирма могла бы установить цену около 61.63-70.98 руб. за литр топлива, тогда монопольная сверхприбыль была бы максимальной. Такая цена топлива нарушает антимонопольный закон и вызвала бы вмешательство ФАС. Соответственно, активным становится ограничение на цену от государства – не более 60,64 руб. за литр в 2023 году. При коррекции стоимости литра топлива по рекомендации ФАС до 60,64 руб. за литр, ожидаемая прибыль значительно уменьшается. Если бы фирма предусмотрела возможное вмешательство ФАС, то могла бы избежать потери при- были, адаптировав объемы выпуска продукции.

Заключение. Разработана дискретная динамическая стохастическая модель частичного равновесия для описания функционирования фирмы в условиях нестабильности внешней среды. В рамках данной модели: построена эмпирическая функция спроса на основе статистических данных с применением метода наименьших квадратов. Также был определен оптимальный объем производства и соответствующая оптимальная прибыль фирмы в виде доверительного интервала с учетом выявленных шоков функции спроса.

Результаты работы могут быть использованы для принятия обоснованных управленческих решений в условиях нестабильности внешней среды.