Управление элементами экзоскелета с изменением параметров рядов Фурье для адаптивной реабилитации пациентов

RUSSIAN JOURNAL OF BIOMECHANICS

Биомеханика является одной из научных дисци- плин, оказывающих значительное влияние на развитие медицины. В частности, следует отметить вклад научных публикаций, посвященных моделированию движений верхних и нижних конечностей [1–4] и поясничного отдела [5–8], а также исследованиям в области спортивной медицины [9; 10] и судебно- медицинской экспертизе дорожно-транспортных происшествий [11]. В этом контексте особое внимание заслуживают статьи, посвященные экзоскелетам, ко- торые основаны на экспериментальных исследованиях направленных на анализ походки человека [12; 13] Экзоскелеты находят широкое применение в различных сферах, включая военную промышленность, про изводственные предприятия и реабилитацию пациентов. Рассмотрим подробнее последнюю сферу приме

0009-0002-9218-4267

0000-0001-5144-6895

Эта статья доступна в соответствии с условиями лицензии Creative Commons Attribution-NonCommercial 4.0 International

License (CC BY-NC 4.0)

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License (CC BY-NC 4.0)

нения экзоскелетов.

Экзоскелет для реабилитации ног – это носимое роботизированное устройство, предназначенное для помощи людям с проблемами подвижности в результате травм, операций или неврологических заболеваний, таких как травмы спинного мозга, инсульт или рассеянный склероз. Экзоскелеты помогают пациентам при восстановлении или улучшении функции ходьбы или выполнении других действий ногами, для имитации естественных движений [14–16]. Компонентами экзоскелета являются датчики, двигатели и приводы, которые помогают контролировать движение суставов, позволяя пациенту стоять и ходить. Многие экзоскелеты оснащены датчиками, которые определяют движения пользователя, позволяя устройству корректировать свои действия соответствующим образом [14–16].

В работе [17] был разработан и исследован реабилитационный экзоскелет нижней конечности. В статье [18] было представлено адаптивное нелинейное управление для системы реабилитации. Исследовались характеристики контроллера и устойчивость к параметрическим неопределенностям. Для управления системой экзоскелета использовали адаптивные частотные осцилляторы [19–22]. Применение этой стратегии управления позволяет экзоскелету адаптироваться к различным ритмам движения пользователя [23; 24]. В исследовании [12] показаны роботизированные устройства для тренировки походки, позволяющие улучшить подвижность пациентов при ходьбе, избегая при этом физического перенапряжения. Предложенные устройства тестировались на пациентах разных возрастных групп (взрослых и детях), и результаты показали их эффективность в соответствии со спецификациями конечных пользователей.

В работе [25] исследована аналитическая стратегия управления положением колена человека. Профиль угла наклона колена был представлен в виде семичленной экспоненциальной функции, которая определялась на основе начального и конечного угла наклона колена, скорости и крутящего момента. В статье [26] был разработан пассивный гравитационный балансирующий экзоскелет с целью изучения изменений в кинематике и кинетике походки пользователя. Динамическая модель движения тазобедренного и коленного суставов, основанная на методе Эйлера – Лагранжа, была представлена в [27]. В источнике [28] была предложена модель походки на основе Solidworks для моделирования системы нижних конечностей. Использование гравитационной балансировки позволяет снизить мощность, необходимую приводу во время движения, за счет использования соответствующих противовесов и пружин [29–31].

В последние годы в многочисленных исследованиях использовались методы аналитического управления для отслеживания опорных параметров системы и достижения целевых условий, включая электрические, механические и электромеханические системы. В работах [32–36] представлены экспоненциальные функции для создания профилей опорных параметров системы при достижении начальных и конечных условий. Аналитические входные данные были успешно использованы для управления и стабилизации систем в различных условиях, отличных от номинальных. В статье [37] использовались полиномиальные функции для формирования инфицированных клеток и вирусной нагрузки с целью лечения хронического гепатита В. Были разработаны два эффективных препарата для заселения инфекции и блокирования распространения вируса.

В текущей статье представлена функциональная методика управления движением человеческой нижней конечности. В первую очередь, в методике используется две функции Фурье по 8 членов каждая для формирования эталонных профилей углов бедра и колена. Затем оцениваются коэффициенты суставов при соблюдении граничных условий в начале, середине и конце времени выполнения движения. В итоге, на основе предложенной функции ряда Фурье определяются крутящие моменты в тазобедренном и коленном суставах, чтобы направить движение ноги, согласно созданным эталонам.

Методология

Модель нижней конечности человека может быть описана двумя углами поворота (β 1 , β 2 ) и двумя крутящими моментами ( T 1 , T 2 ) в тазобедренном и коленном суставах соответственно. На рис. 1 представлена предлагаемая модель.

Математическая модель нижней конечности человека описывается двумя дифференциальными уравнениями второго порядка [38]. Модель, представленная на рис. 1, получена с помощью метода Лагранжа

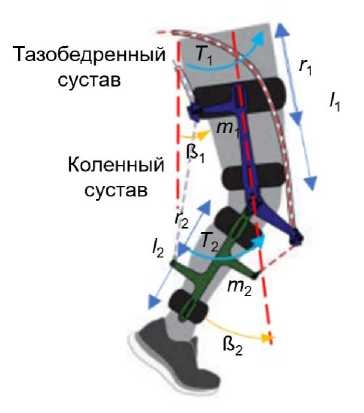
Рис. 1. Экзоскелет нижней конечности человека [39]

d dKe dt ^ap.

dKe  dU  dV

---1---+—⁷— = T, j = 1,2, dp.   dp.   dp. j

где K e , U и V – кинетическая, потенциальная и дисси-пационная энергии соответственно. Два дифференциальных уравнения второго порядка (А1) и (А2) представлены в приложении, где m 1 , ℓ 1 и r 1 – масса верхней части ноги, длина верхней части ноги, расстояние от тазобедренного сустава до центра верхней части ноги соответственно, а m 2 , ℓ 2 и r 2 – масса нижней части ноги, длина нижней части ноги, расстояние от коленного сустава до центра нижней части ноги соответственно.

Поскольку система включает в себя две зависимые переменные (углы наклона бедра и колена), необходимо учитывать ранг двух дифференциальных уравнений второго порядка. В результате крутящие моменты в тазобедренном и коленном суставах могут быть получены решением уравнений (А1) и (А2) (см. приложение) для T 1 , T 2 , как показано в уравнениях (2) и (3) соответственно:

T =

Э1 ( m l ' I² + m 2 r 2 ) + m 2^ r 2 ₽ 2 cos ( P 1 -₽ 2 ) ^{+ C} 1 P 1 ^+ m^r P 2 sin (Д -P₂ ) + g sin Pi ( m' + m ₂^i) _?

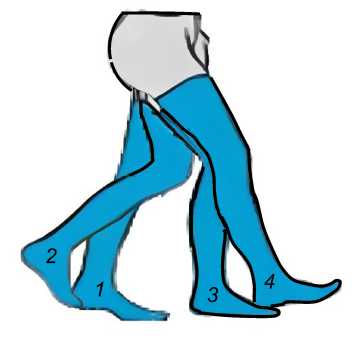
Рис. 2. Изменение углов наклона бедра и колена

бедра и колена на основе функций ряда Фурье, удовлетворяющих граничным условиям системы. Полученное аналитическое решение покажет эталонные траектории.

Опорные углы бедра и колена описываются с помощью функций ряда Фурье, как показано в уравнениях (4) и (5) соответственно:

T =

T 2

P l m 2 A r > P 2 cos ⁽P 1   P 2 ^{) +} m 2 ^Г 2 P 2

^ т₂£г p 2 sin ( pj -p₂ ) + m₂r₂g sin P₂ + c ₂p₂^

P refl

E i=1

(^{- 1} ) ' ^{+ 1 Г} 2 n - 1 sin ( ( ^{2i - 1} ) t ) +

( - 1 ) ' ^{+ 1} Г i cos ( 2it )

Крутящие моменты в тазобедренном и коленном суставах являются главными в управлении движения нижней конечности человека. Поэтому очень важно разработать адекватный метод, который бы эффективно находил необходимые крутящие моменты, тем самым помогая и направляя движения пациента на протяжении всего курса лечения. В данной работе представлена инновационная методология, использующая математические инструменты для управления движением нижней конечности человека. По методике рассчитываются крутящие моменты системы, основываясь на предположении, что движения бедра и колена соответствует поведению функции ряда Фурье. Эти модели описывают движения тазобедренного и коленного суставов с помощью суммы функций синуса и косинуса. Углы наклона тазобедренного и коленного суставов варьируются в диапазоне между – 20 и 20; 0 и 50 ° соответственно. На рис. 2 представлены режимы изменения углов тазобедренного и коленного суставов в заданных пределах. В режиме 1 бедро находится под углом – 20 °, а колено под углом 0 °. Режим 2 показывает угол бедра 0 ° и угол колена 50 °. Режим 3 показывает угол бедра 20 ° и угол колена 50 °. В режиме 4 угол наклона бедра установлен на 20 °, а угол наклона колена на 0 °.

В первую очередь, необходимо определить крутящие моменты для приведения ноги из исходного состояния в эталонное, придерживаясь заданной траектории. Первый шаг – создание угловых профилей

P ref 2 =

E i=1

(^{- 1} ) ‘ ^{+ 1 P} 2 n - 1 sin ( ( ^{2i - 1} ) t ) ⁺

( - 1 ) ' ^{+ 1} P ₂₁ cos ( 2it )

где ℾ i и P i – коэффициенты, параметризующие движения бедра и колена соответственно.

Эталонные угловые скорости бедра и колена могут быть получены из уравнений (6) и (7) соответственно:

Pref1 =E i=1

Pref2 =E i=1

( 2 i - 1 )( - 1 ) i ^{+ 1} Г 2 _; - 1 Cos ( ( 2 i - 1 ) t )

- 2 i ( - 1 ) " ^{+ 1} Г_2; sin ( 2 it )

( 2 i - 1 )( - 1 ) i ^{+ 1} P 2 n - 1 Cos ( ( 2 i - 1 ) t )

-2i ( - 1 ) 1⁺¹ P_2t sin ( 2 it )

,

,

Тогда эталонные угловые ускорения бедра и колена могут быть выражены уравнениями (8) и (9) соответственно

P ref1 = E i = 1

7 2 i - 1 ) ² ( - 1 ) i ^{+ 1} Г 2 i - 1 Cos ( ( 2 i - 1 ) t f

₄- 4 i ² (^{- 1} ) i ^{+ 1 Г} 2 i sin ( ²ⁱt )             _?

Pref2 =E i=1

7 2i - 1 ) ² ( - 1 ) i ^{+ 1} P 2 i - 1 Cos (( 2i - 1 ) t f ,- 4 i ² (^{- 1} ) i ^{+ 1 P} 2 , . sin ( ² it )              _?

Таблица 1

Граничные условия для нижней конечности человека

Параметр	Начальное состояние	Среднее состояние	Конечное состояние
Угол наклона бедра, °	– 20	20	– 20
Угол наклона колена, °	0	50	0
Скорость движения бедра, рад/с	0	0	0
Скорость движения колена, рад/с	0	0	0
Ускорение бедра, рад/с2	0	—	0
Ускорение колена, рад/с2	0	–	0
Время, с	0	0,5	1

Подставив уравнения (4)–(9) в уравнения (2) и (3), мы получим крутящие моменты тазобедренного и коленного суставов, представленные в приложении в формулах (А3) и (А4) соответственно.

По уравнениям (А3) и (А4) получены необходимые опорные переменные управления для обеспечения точного движения ноги. Однако для этого необходимо рассчитать 16 коэффициентов: восемь для создания эталонного профиля угла наклона бедра и остальные для определения профиля угла наклона колена. Таким образом, для вычисления 16 параметров (ℾ i , P i ) необходимо задать восемь граничных условий для каждого сустава.

В первую очередь, эталонный профиль угла наклона бедра формируется с помощью одной пары углов наклона бедра ( t 0 , β 1-0 ), скорости бедра ( t 0 , β 1-0 ) и ускорения бедра ( t 0 , β 1-0 ) в начальном положении. В конечном положении определяется одна пара: угол наклона бедра ( t f , β 1- f ), скорость бедра ( t f , β 1- f ) и ускорение бедра ( t f , β 1- f ). Кроме того, рассматривается одна пара из угла наклона бедра ( t m , β 1- m ), скорости бедра ( t m , β 1- m ) и ускорения бедра ( t m , β 1- m ).

Аналогичным образом эталонный профиль угла колена формируется с помощью одной пары углов колена ( t 0 , β 2-0 ), скорости колена ( t 0 , β 2-0 ) и ускорения колена ( t 0 , β 2-0 ) в начальном положении. В конечном положении определяется одна пара угла наклона колена ( t f , β 2- f ), скорости колена ( t f , β 2-f ) и ускорения колена ( t f , β 2- f ). Кроме того, рассматривается одна пара из угла наклона колена ( t m , β 2- m ), скорости колена ( t m , β 2- m ) и ускорения колена ( t m , β 2- m ).

В табл. 1 указаны граничные условия на нижней конечности человека, необходимые для формирования угловых профилей бедра и колена.

Чтобы получить соответствующие крутящие моменты системы, недостающие коэффициенты будут подставлены в уравнения (А3) и (А4) после применения граничных условий системы.

Крутящие моменты бедра и колена вычисляются аналитически путем определения 16 коэффициентов нижней конечности, исключая любые замкнутые системы управления. Таким образом, алгоритм способен автоматически удовлетворять желаемым положениям в системе нижних конечностей, когда известны граничные условия (начальные, промежуточные и конечные).

Результаты и их обсуждение

Основная цель алгоритмов управления движением нижней конечности человека – перемещение ноги по опорной траектории с учетом ограничений на управление и положение. Как правило, система строится на основе двух концепций: определения опорной траектории и разработки подхода к управлению для ее соблюдения. В данной работе, как уже говорилось ранее, была предложена новая аналитическая методология, которая позволяет эффективно направлять человеческую ногу на отслеживание сформированной рефлекторной траектории без использования управления с обратной связью.

На рис. 3 представлены профили углов наклона бедра и колена в зависимости от времени. Крутящие моменты эффективно направляют человеческую ногу для достижения желаемого положения, точно отслеживая заданные профили углов бедра и колена. Результаты подтверждают целесообразность предложенной схемы Фурье, гарантируя, что ни максимальный крутящий момент бедра ( T 1max = 90 Н⋅м), ни максимальный крутящий момент колена ( T 2max = 45 Н⋅м) не будут превышены [40]. На рис. 3 углы наклона бедра и колена начинаются с начальных условий β 1-0 = – 20 ° и β 2-0 = 0 ° соответственно и варьируются, достигая средних значений углов β 1-0 = 0 ° и β 2-0 = 50 ° соответственно. Затем они находятся в допустимых пределах, чтобы захватить желаемые углы бедра и колена β 1-0 = 20 ° и β 2-0 =0 ° соответственно с шагом в 1 с.

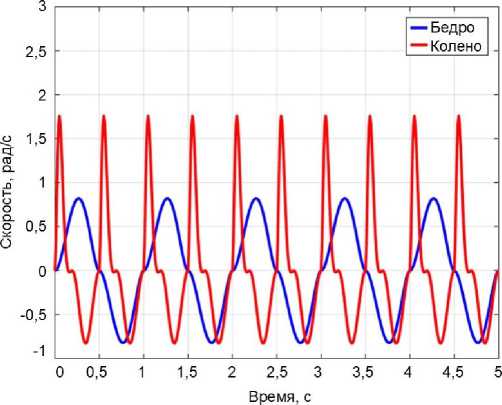
На рис. 4 показаны профили угла наклона бедра и колена, скорости движения и крутящего момента в зависимости от времени на пяти временных шагах,

а                                                       б

в

Рис. 3. Исходные положения нижней конечности в зависимости от времени: а - углы наклона бедра и колена; б - скорости бедра и колена; в - крутящие моменты чтобы показать движение нижней конечности человека на различных временных шагах.

Как показано на рис. 4, a , угол наклона тазобедренного сустава изменяется от - 20 ° до 20 °, а угол наклона коленного сустава от 0 ° до 50 °. В практическом смысле эти результаты соответствуют динамике взмахов ног человека. На рис. 3, a , показано, что угол тазобедренного сустава имеет меньшую амплитуду и более низкую частоту по сравнению с коленным суставом. На рис. 4, б , представлено движение тазобедренного сустава, которое происходит медленнее коленного. В конце процесса (рис. 4, в ) тазобедренный сустав требует больше усилий, чем коленный, из-за сложной структуры тазобедренного сустава, в то время как оба крутящих момента находятся в пределах допустимых ограничений для нижней конечности.

Надежность и работоспособность предложенного алгоритма нуждается в рассмотрении модели при различных характеристиках пациента.

Для решения этой проблемы будет применен метод моделирования Монте-Карло для проверки работы предложенного контроллера при нестандартных сценариях [41-43]. Метод Монте-Карло - это статистическая методология, применяемая для анализа и реализации поведения динамических систем с большим числом случайных положениях [44; 45]. В исследовании эффективность предложенного метода проверяется по характеристикам пациентов, таких как масса верхней и нижней части ноги и широкий диапазон начальных углов наклона бедра и колена. В табл. 2 представлены нестандартные и нормальные характеристики тела человека.

Наконец, в моделировании методом Монте-Карло участвовали 500 пациентов с широким диапазоном параметров системы и разбросом условий.

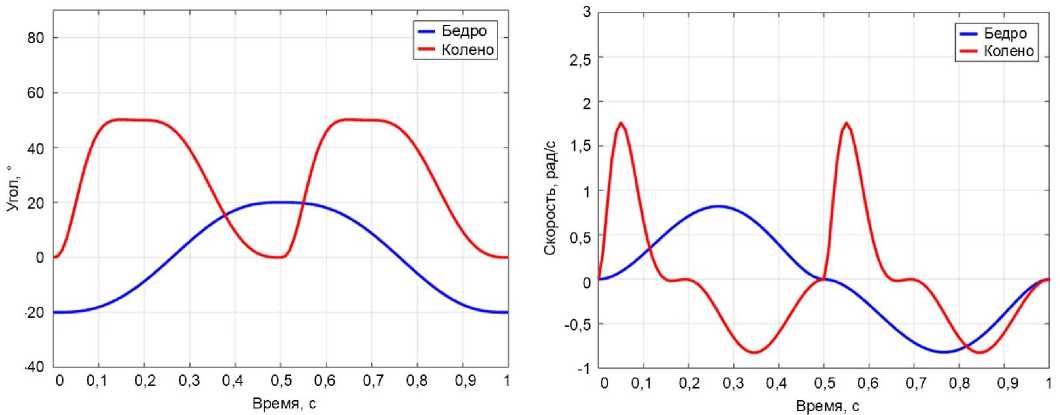
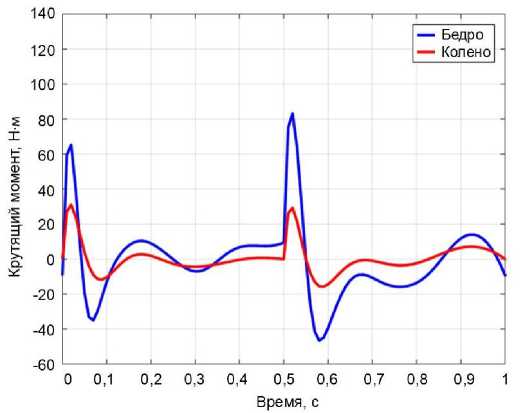
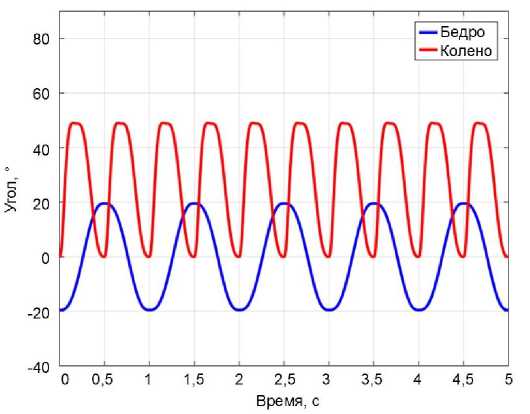
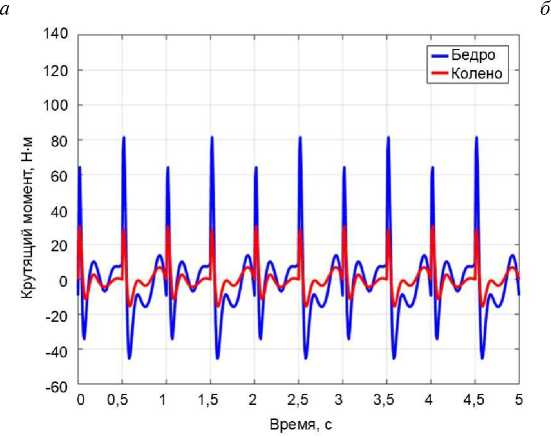
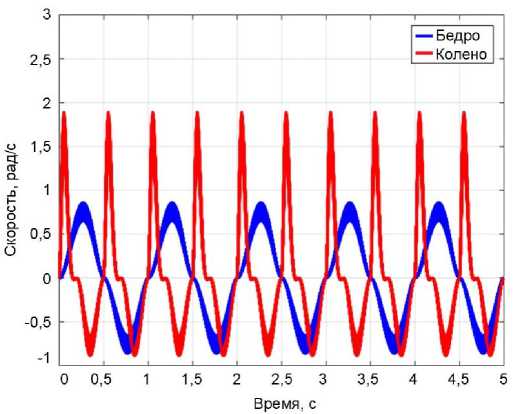
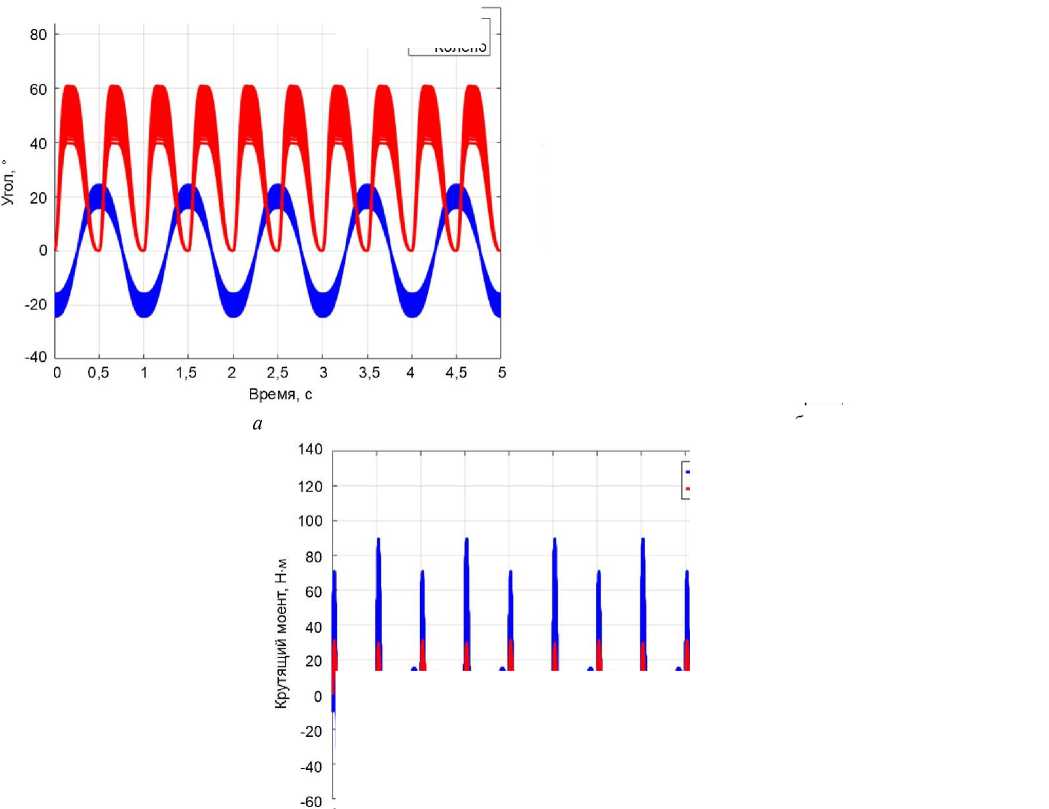
На рис. 5 показаны графики углов, скоростей и крутящих моментов в тазобедренном и коленном суставах в зависимости от времени. На рис. 5, а и б

в

Рис. 4. Эталонные и смоделированные профили бедра и колена в зависимости от времени с использованием функции Фурье в номинальных условиях в течение 5 шагов: а – углы наклона бедра и колена;

б – скорости бедра и колена; в – крутящие моменты бедра и колена

Таблица 2

Нормальные и нестандартные характеристики тела

Параметр Нормальное значение Максимальное значение Минимальное значение Масса верхней части ноги, кг 8,0 8,5 7,5 Масса нижней части ноги, кг 2,75 3,25 2,25 Начальный угол наклона бедра, ° 20,0 25,0 15,0 Начальный угол наклона колена, ° 50,0 62,5 37,5 тазобедренный и коленный суставы точно следуют сгенерированным ориентирам, несмотря на широкий диапазон характеристик пациента. Кроме того, на рис. 5, в показано, что для перемещения суставов ног требуется меньший крутящий момент, чем допустимые пределы, при всех случаях моделирования.

Результаты Монте-Карло подтверждают эффективность и надежность метода к отслеживанию заданных параметров без превышения ни максимального крутящего момента бедра (T1max = 90 Н⋅м), ни максимального крутящего момента колена (T2max = 45 Н⋅м).

Заключение

Из результатов предложенной методики к управлению можно сделать следующие выводы:

б

— Бедро

— Колено

— Бедро

— Колено

О 0.5

1,5    2    2,5    3    3,5    4    4,5    5

Время, с

в

Рис. 5. Динамика ног человека в зависимости от времени с использованием функции Фурье для тазобедренного и коленного суставов: а – угол; б – угловая скорость; в – крутящий момент

• 1.    Предложенные функции Фурье обеспечили крутящие моменты, которые эффективно позволили человеческой нижней конечности достичь желаемых положений, точно отслеживая заданные профили углов бедра и колена с высокой стабильностью.

• 2.    Отклики тазобедренного и коленного суставов были надежными и соответствовали сформированным траекториям в допустимых пределах, несмотря на значительные изменения параметров системы и дисперсии начальных условий.

• 3.    Коленный сустав показал максимальную скорость V knee = 1,92 рад/с и частоту около 1,86 Гц, в то время как тазобедренный сустав зарегистрировал максимальную скорость V hip = 0,82 рад/с и частоту около 0,93 Гц. Эти значения полностью совпадают с экспериментальными данными, полученными во время ходьбы [46; 47].

• 4.    Коленный сустав испытывал более быстрые и частые колебания значений по сравнению с тазобедренным суставом, что объясняется структурной про-

• стотой коленного сустава по сравнению со сложным образованием тазобедренного сустава.

• 5.    Наблюдаемый максимальный крутящий момент в тазобедренном суставе был определен как T 1 = 89 Н⋅м, в то время как в коленном суставе он составил T 2 = 39 Н⋅м. Разница в значениях объясняется тем, что тазобедренный сустав окружен более обширной и биомеханически сложной группой мышц по сравнению с коленным суставом, поэтому ему требуется большее усилие для движения в различных направлениях.