Управление корпорацией на основе мультиобъектного подхода

Если норма прибыли для всех предприятий одинакова и равна α , то конечная цена равна n

P = 5 (1 + a ) n ^{+ 1 - j} C + .           (2)

j = 1

Для той же самой технологической цепочки в случае, если n предприятий входят в консорциум, цена конечного продукта будет следующая:

n

Pk = (1 + a )£ C(3)

j = 1

Определим разность P и P_k .

nn

P - Pk = Z (1 + a) n+HC- (1 + a )5 C+ = j=1

n

= (1 + a )£ C+( (1 + a) n-j-1).(4)

j = 1

Эта разность всегда неотрицательна, в случае α = 0 она равна 0, в остальных случаях она

ВЕСТНИК 2013 № 2

положительна, то есть в концерне цена на конечный продукт меньше.

Определим эффективность организации предприятий в корпорацию как отношение

уменьшения цены конечного продукта к цене, получаемой при корпоративной деятельности.

Проиллюстрируем полученную зависимость.

Таблица 1

Зависимость эффективности организации предприятий в корпорацию (А) от числа предприятий и нормы прибыли

(1 + а ) Z C +( (1 + а ) n - j - 1 ) A = P  P k =       j = 1                  =

P         (1 + а ) £ C + J = 1

Z C + ( (1 + а ) n-j - 1 )

= j = 1         n                 .             (5)

z c ; i = 1

Пусть все предприятия привносят одинаковую дополнительную себестоимость:

£ ( (1 + а ) ⁿ - j - 1 ) £ (1 + а ) ⁿ - j - n

A = j1-----------= j1---------- nn

ВЕСТНИК 2013 № 2

n

Z (1 + а)n-j j=1

1(1 - (1 + а ) ⁿ ) 1 - (1 + а )

^{(1 + а} ) n ^{- 1}; (6) α

(1 + а ) ⁿ - 1

--n

A =---а------ n

(1 + а ) ⁿ - 1 - а n

α n

02 3S H S у H i * S к к	Норма прибыли ( a )
	0,2	0,4	0,6	0,8	1
1	0,00	0,00	0,00	0,00	0,00
2	0,10	0,20	0,30	0,40	0,50
3	0,21	0,45	0,72	1,01	1,33
4	0,34	0,78	1,31	1,97	2,75
5	0,49	1,19	2,16	3,47	5,20
6	0,65	1,72	3,38	5,88	9,50
7	0,85	2,41	5,15	9,75	17,14
8	1,06	3,30	7,74	16,06	30,88
9	1,31	4,46	11,54	26,41	55,78
10	1,60	5,98	17,16	43,51	101,30
11	1,92	7,98	25,50	71,92	185,09
12	2,30	10,60	37,95	119,40	340,25

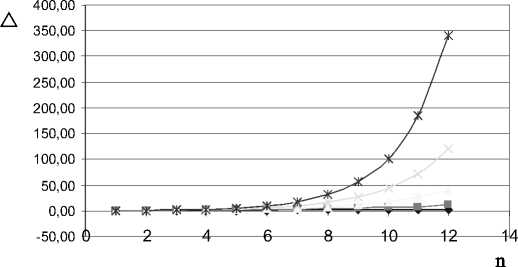
Рис. 1. Зависимость эффективности организации предприятий в корпорацию (Δ) от числа предприятий ( n ) и нормы прибыли ( α )

Представленные данные свидетельствуют о том, что чем выше норма прибыли предприятий и чем больше их число, тем выгоднее в плане снижения цены конечного продукта их интеграция в корпорацию.

Из полученного результата следует необходимость интеграции предприятий в рамках технологической цепочки.

Задача принятия решений в вертикально или горизонтально интегрированной корпорации хорошо решается при помощи дерева критериев, где каждый проект характеризуется набором критериев, определяемым лицами, принимающими решения (ЛПР). Агрегированные критерии получаются на основе критериев, определенных или рассчитанных ЛПР, по правилам, представленным в виде таблиц агрегирования. Любая задача агрегирования сводится к построению бинарного критериального дерева, где каждому критерию нижнего уровня сопоставле- ны определенные проекты, обеспечивающие достижение определенного уровня, а также соответствующие затраты. Происходит построение набора, позволяющего с минимальным уровнем затрат достичь оптимальных результатов, для чего выявляют напряженные состояния по всем представленным критериям [1].

Данный метод принятия решений можно значительно усовершенствовать, если рассматривать критерии любого уровня не в качестве значений, которые либо предоставляются ЛПР, либо получаются при помощи таблиц агрегирования, а как объекты, обладающие определенным набором свойств, определяющих состояние среды. Такое изменение позволяет расширить круг задач, решаемых при помощи критериальной схемы, так как для расчета результирующих критериев часто требуется целый набор дополнительных сведений, характеризующий исходное состояние среды. Допустим, требуется определить агрегированное значение степени осведомленности клиентов о продукте на рынке Российской Федерации, если в Москве о нем знают 17%, в Санкт-Петербурге – 3%, в Новосибирске – 2% клиентов. В этом случае объекты таблиц агрегирования должны иметь как минимум

Главное свойство объекта АВ 3	AB 3 =F AB3 (AB 3 ,A A ʼ,Bʼ) (В данном случае АВ 3 =2)
Набор свойств AB 3s (sЄ[1;k])	Набор дополнительных свойств объекта AB 3
Набор свойств Aʼ от исходного объекта А – Aʼ v Є (A 31 , A 32 ‚ …‚ А 3m ) (vЄ[1;m])	Необходимые свойства копируются из объекта-источника, количество скопированных свойств больше или равно 0, но не больше числа свойств объекта А

O AB3

AB 3 =2

Главное свойство объекта А 3

A 3 =F A3 (A 31 , A 32 ‚ …‚ А 3m ) (В данном случае А 3 =2)

два свойства: процент осведомленной клиентуры и размер населения города – чтобы произвести пересчет для всего населения региона. Если мы будем знать только первое значение, то мы не сможем определить агрегированный критерий.

Согласно мультиобъектной схеме, все объекты, принадлежащие одной таблице, имеют одинаковую структуру. Агрегированные объекты изменяют значения своих свойств на основании значений свойств исходных объектов, а также правил, определяемых ЛПР. Одно из свойств каждого из объектов функционирует как обыкновенный критерий – агрегированный, или предоставляемый ЛПР. Такие свойства, назовем их основными, определяют значения, откладываемые по осям таблиц агрегирования. Объекты могут хранить свойства, не являющиеся необходимыми для расчета собственных основных свойств, но требуемые для определения своих неосновных свойств, или основных свойств объектов большей степени агрегации.

В самом своем простом варианте, когда объекты имеют только основные свойства, схема превращается в обыкновенную модель принятия решений с вычислением критериев на основе значений предыдущего уровня [1].

ВЕСТНИК 2013 № 2

AB 2 =1

150	800	750
150	750	300
150	150	300

С-во А 31

C-ʙo A 32

F A31 (A 32 , …, A 3m )

F A32 (A 31 , A 33, …, A 3m )

OA2 }^

CD CD 1 =15 CD 2 =20 CD 3 =30

O CD1	O CD2	O CD3

A 3 =2

A 2 =1

B

1	1	2
0	1	2
0	1	2
B 1 = 0 B 2 =1   В з =2 O B1    O B2    O B3

C 3 =2

D

C 2 =1

15	20	30
15	10	20
15	15	10

D 1 = 0 D 2 =1   D 3 =2

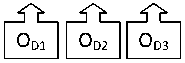
Рис. 2. Мультиобъектная схема при одинаковых неосновных свойствах одноуровневых объектов

ВЕСТНИК 2013 № 2

При упрощенном варианте работы (см. рис. 2) все объекты одного уровня имеют не только одинаковую структуру, но и одинаковые значения неосновных свойств (при определении информированности населения основным свойством выступает процент осведомленных людей, а неосновным – численность населения города, региона и так далее).

И в этом случае алгоритм работы аналогичен изложенному в работе [1], но при вычислении критериев верхнего уровня дополнительно используются значения неосновных свойств текущего и нижних уровней. На вход таблиц агрегирования подаются критериальные объекты нижнего уровня, например объект А₃, который имеет m неосновных свойств, определяемых как значения нециклических функций от других свойств. Частным случаем функции является константа. Агрегированный критериальный объект AB₃, полученный в трех элементах таблицы AB, ввиду однородности структур одноуровневых объектов и равенства соответствующих неосновных параметров объектов А и В может наследовать некоторые свойства объектов А, B и вычислять свои собственные свойства как нециклические функции от унаследованных или добавленных свойств. Напряженные варианты выбираются стандартным образом.

Самый сложный вариант работы с мульти-

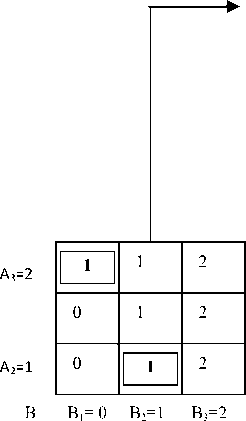
объектной схемой возникает, когда однородные (с одинаковой структурой) критериальные объекты имеют разные значения неосновных свойств. В этом случае может возникнуть коллизия – ситуация, когда при разных состояниях исходных объектов-критериев их основные свойства совпадают. Если коллизий не возникает, то работа производится согласно описанию в работе [1]. Коллизии опасны из-за того, что значения агрегированных критериев старшего уровня могут быть различными для разных исходных объектов, основные свойства которых совпадают, поэтому есть вероятность потери значений агрегированного критерия, если исходные критериальные объекты будут восприняты как один из-за равенства их основных свойств. Чтобы этого не произошло, в таблице агрегирования следующего уровня по одной из критериальных осей откладывают два (или более) одинаковых значения, соответствующих разным объектам (см. рис. 3).

На рисунке приведен пример коллизии. Объект C2D3 имеет одинаковое значение основного свойства с объектом C3D2 при разных значениях неосновных свойств. Если бы мы не разделили объекты на оси Х таблицы ABCD, то нам бы пришлось включить планы A3 = 2, B1 = 0, C2 = 1, D3= 2 и A1= 0, B2= 1, C2= 1, D3= 2 в набор напряженных вариантов. Но на рисунке видно, что в

O A3 >

OA2 }^

O A1 J^

O AB3^ AB 3 =2	150	800	700	750
OAB2 г^ AB 2 =1	150	750	300	300
OAB1 г>	150	150	200	300
CD	CD 1 =15	C 3 D 2 =20	C 2 D 3 =20	CD 3 =30

O C3> C 3 =2	15	20	30
OC2}^	15	10	20
OC1 J^ C 2 =1	15	15	10
D	D 1 = 0 D 2 =1   D 3 =2 O D1    O D2    O D3

Рис. 3. Мультиобъектная схема при разных неосновных свойствах одноуровневых объектов колонке объекта C2D3 таблицы ABCD нет напряженных элементов (заметьте, что столбец C2D3 сравнивается со столбцом CD1).

Современные средства объектно ориентированного программирования (ООП) идеально подходят для создания визуальной среды построения мультиобъектной схемы принятия решений. Критериальные объекты реализуются в виде компонентов, где свойства объектов становятся компонентными свойствами, а правила агрегирования – методами, осуществляющими их установку. Автоматизация мультиобъектной схемы принятия решений позволит, во-первых, ускорить работу и получить множество вариантов развития ситуации, и, во-вторых, охватить больший диапазон задач, чем в случае использования простого дерева критериев.