Управление космическим аппаратом дистанционного зондирования Земли с помощью роторов

Задачи нацеливания космического аппарата (КА) на определенный объект земной поверхности не теряет своей актуальности. Одним из наиболее распространенных способов переориентации КА дистанционного зондирования Земли (ДЗЗ) для нацеливания камеры или антенны является использование двигателей малой тяги, которые подразделяются на несколько категорий: на сжатом газе, на монотопливе на двухкомпонентном топливе; специальные установки и двигатели на закиси азота, аммиаке, газообразных водороде и кислороде; электроракетные системы на базе импульсных плазменных, ионных и стационарных плазменных двигателей [1].

Все вышеперечисленные способы подразумевают использование рабочего тела, запас которого ограничен на борту КА. Для решения проблемы с топливом предлагается использовать двигатели-маховики на основе управляемого моментного бесконтактного двигателя постоянного тока 1. Подобные КА называют спутниками-гиростатами. Данный способ является более эффективным из-за отсутствия необходимости в расходе рабочего тела, как следствие, уменьшения рабочей массы КА.

Задаче исследования движения гиростатов посвящено достаточно много работ отечественных и зарубежных ученых, например, В. В. Румянцева [2; 3], В. Н. Кошлякова [4], А. И. Нейштадта и М. Л. Пивоварова [5], Й. Виттенбурга [6], В. С. Асланова и А. В. Дорошина [7; 8] и многих других. В подавляющем большинстве работ исследуются динамика и устойчивость движения гиростатов, но мало внимания уделяется определению законов движения и управляющих воздействий, обеспечивающих данные движения.

В статье [9] приведено построение управления КА с помощью одного ротора для нацеливания на объект, который находится в плоскости орбиты КА. В данной работе ставится задача нахождения управляющих моментов, действующих на роторы гиростата для нацеливания на объект, находящийся вне плоскости орбиты КА ДЗЗ.

1 Математическая модель

Предположим, спутник представляет собой динамически несимметричное тело (тело 4) с тремя одинаковыми динамически симметричными роторами (тела 1, 2, 3), оси вращения которых совпадают с главными осями инерции всей системы (рис. 1). Вывод математической модели движения подобных систем приведен в разных работах [2–8]. Для наглядности и удобства обозначения координатных осей и других параметров на рисунке 1 роторы изображены схематично (вне несущего тела). На самом деле роторы находятся внутри КА.

Динамические уравнения движения строятся на основании теоремы об изменении кинетического момента механической системы и примут вид:

Ap + (С - B)qr + Io 1 +1(qo3 - ro2) = Mx;

Bq + (A - C)pr + Id2 +1(ro1 - po3) = My;(1)

Ci- + (B - A)pq + Io3 +1(po2 - qo1) = Mz, 4              44

где A = £ Ai, B = £ Bi, C = £ Ci; Ai, Bi, Ci (i = 1, 2, 3) — главные момен-i=1                 i=1

ты инерции роторов, вычисленные в своих связанных системах координат Ox i y i z i ( i = 1, 2, 3), а моменты инерции тела-носителя в системе координат Oxyz - A 4 , B₄, C₄ ; p, q, r — проекции угловой скорости несущего тела на оси системы координат Oxyz ; I = A 1 = B ₂ = C ₃ — осевые моменты инерции роторов. Правые части уравнений (1) представляют собой проекции момента внешних сил.

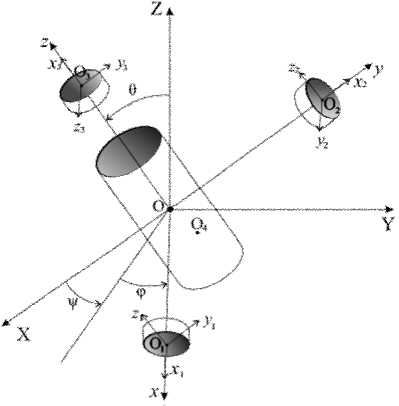
Рис. 1. Схема спутника гиростата и используемые системы координат

Кинематические уравнения для углов Эйлера несущего тела и углов относительного закручивания роторов:

p = / sin 9 sin ф + 9 cos ф ;

q = / sin 9 cos ф - 9 sin ф ;

r = / cos 9 + ф ;

o, = ct; o2 = в o3 = Y, где у, 9, ф — углы Эйлера, которые характеризуют положение несущего тела относительно кениговой системы OXYZ; а, в, у — углы относительного закручивания роторов; ох, <г2, <73 — относительные угловые скорости роторов.

Уравнения относительного движения роторов:

A 1 ( p + ⁷ 1 ) = M 1 х + M а ;

B 2 (q + 7 2 ) = M 2 у + M в ; C 3 (Г + (7 3 ) = M 3 z + M Y, где Ma, Mp, MY — моменты внутреннего взаимодействия тел вдоль оси вращения; M 1 X, M2y, M3z — моменты внешних сил, действующие на роторы.

Компоненты векторов угловых скоростей роторов 0 ) 1 ( p 1 , q 1 , r 1 ) , со ₂ ( p ₂ , q ₂ , r ₂ ) , О ₃ ( p ₃ , q ₃ , r ₃ ) , выраженные через компоненты угловой скорости несущего тела, имеют вид:

p 1 = p + ⁷ 1 ;

q 1 = q cos а + r sin a ; <  r 1 = r cos a - q sin a ,

p 2 = p cos в - r sin P ; q 2 = q + ⁷ 2 ;

r ₂ = r cos в + p sin P ,

p 3 = p cos Y + q sin y ;

q ₃ = q cos y - p sin y ; (4) r ₃ = r + < 7 ₃ .

Таким образом, уравнения (1) - (4) представляют собой замкнутую математическую модель движения спутника-гиростата относительно центра масс. Приведенные уравнения при добавлении начальных условий позволяют определить все параметры движения системы в зависимости от времени.

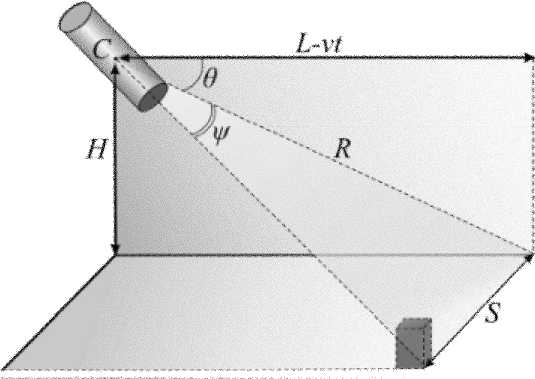
Рис. 2. Схема движения спутника-гиростата

С учетом перечисленных допущений уравнения движения спутника-гиростата преобразуются. Первые три из кинематических уравнений (2) примут вид:

p = 9;

q = у sin 0 ;                              (5)

r = у cos 0 .

Уравнения относительного движения роторов (3) запишутся следующим образом:

A 1 ( p + ⁷ 1 ) = M a ;

B 2 ⁽ q + ⁷ 2 ) = M в ;

C 3 ( r + 7 3 ) = M , .

В уравнениях (1) правая часть обнулится, а уравнения (4) не изменятся.

Таким образом, ставится задача определения внутренних управляющих моментов M _a , M _р , M _Y , обеспечивающих нацеливание КА ДЗЗ на объект наблюдения в течение некоторого интервала времени.

3 Определение управляющих моментов

0 и

В течение всего времени t активного участка полета углы нутации прецессии у могут быть определены по формулам (рис. 2):

L — vt

0 = arcctg H ,

7 H ² + ( L — vt ) ²

у = arcctg----------------.

Подставим данные значения углов нутации (6) и прецессии (7) в кинематические уравнения (5), получим зависимости проекций угловой скорости несущего тела от времени:

Р =

Hv

H ² + ( L - vt ) ² ’

_            HSv (L - vt)

q (H2 +(L-vt)2)(S2 + H2 + (L -vt)2)’ r  ______________Sv (L - vt)2______________

(H2 +(L -vt)2) (S2 + H2 + (L -vt)2).

Численно проинтегрируем систему дифференциальных уравнений (ДУ) (1) с учетом (8) при соответствующих начальных условиях. На рисунках 3-4 представлены зависимости относительных скоростей и ускорений роторов от времени.

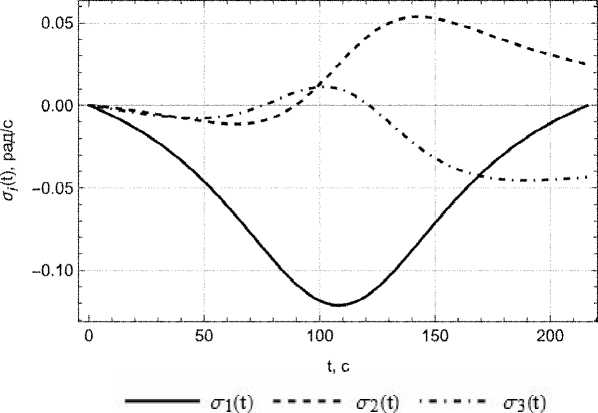
Рис. 3. График зависимостей относительных скоростей от времени

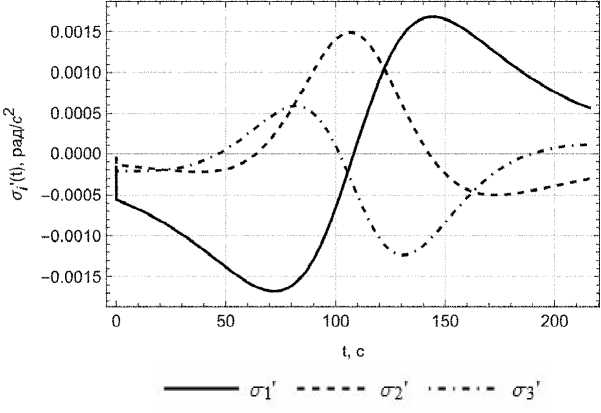
Рис. 4. График зависимостей относительных ускорений от времени

Подставим значения ускорений из решения системы ДУ (1) в уравнения относительного движения роторов и построим график зависимости управляющих моментов от времени (рис. 5).

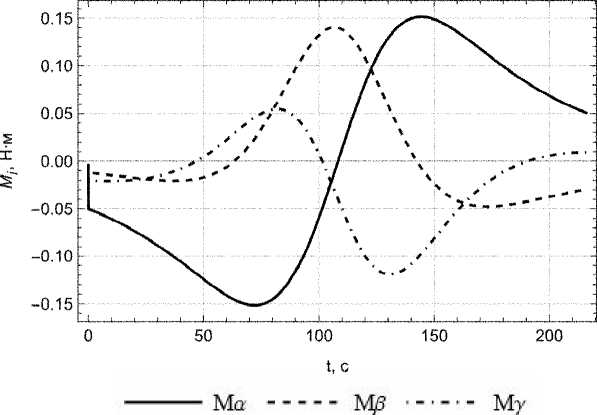
Рис. 5. График зависимостей управляющих моментов от времени

Полученные диапазоны значений управляющих моментов могут обеспечить двигатели-маховики, приведенные в [9].

Для визуального подтверждения верности полученных результатов построена анимация, визуализирующая движение спутника гиростата вблизи объекта наблюдения. Ось цилиндра, схематично изображающего

КА ДЗЗ, должна быть сонаправлена с прямой, соединяющей центр цилиндра и объект наблюдения. На рисунках 6–7 видно, что спутник точно направлен на объект наблюдения, что подтверждает работоспособность математической модели.

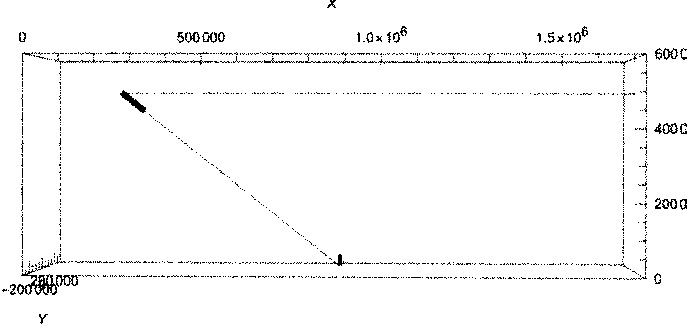
Рис. 6. Кадр визуализации, показывающий угол нутации θ

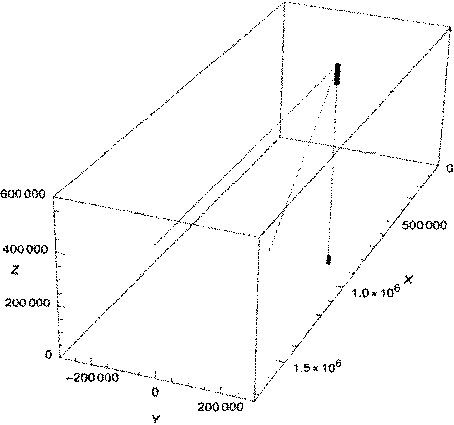
Рис. 7. Кадр визуализации, показывающий угол прецессии ψ

Заключение

В качестве основных результатов работы следует отметить определение законов изменения углов нутации и прецессии, обеспечивающих нацеленность КА ДЗЗ на объект наблюдения, получение зависимостей внутренних управляющих моментов от времени, оценку величины управляющего момента. Кроме того, проведено численное моделирование движения для проверки адекватности аналитических зависимостей.

Результаты работы могут быть использованы при проектировании КА ДЗЗ, использующих для переориентации частичную закрутку (маховики), а также для расчетов и моделирования движения существующих спутников-гиростатов.