Управление параметрами солнечно-синхронных орбит спутников-осветителей

В период полярной ночи в городах, находящихся севернее полярного круга, Солнце не показывается в течение месяцев над горизонтом, и круглые сутки темно. Для освещения таких населенных пунктов предлагается разместить на орбите Земли группировку спутников, оснащенных отражателями большой площади. Управляя положением каждого такого зеркала, можно добиться попадания отраженного солнечного света в район нужного города. Это повысит уровень освещенности заданной местности. В работах [1–3] говорится, что для достижения непрерывной в течение суток освещенности не менее 2 лк необходимо не менее 40 таких спутников, расположенных на низких круговых солнечносинхронных орбитах, при этом поясняется причина выбора именно такого типа орбит.

На космические аппараты (КА), расположенные на орбите Земли, постоянно действуют возмущающие силы, обусловленные несферичностью гравитационного поля Земли, притяжением со стороны Луны и Солнца, сопротивлением атмосферы. Также при освещении города световой поток оказывает регулярное давление на солнечный парус, и возникает периодическая возмущающая сила. Все эти воздействия приводят к вековому уходу параметров орбиты КА.

Для удержания спутников-осветителей вблизи требуемой орбиты управление предлагается осуществлять следующим образом: для коррекции траектории использовать силу солнечного давления. Однако предлагается это делать только на тех участках траектории, где спутник потенциально не может осветить цель, т. е. когда зеркало не используется для своей основной задачи — отражения солнечных лучей в заданный район Земли.

Участки траектории, на которых КА может осветить цель, будем называть рабочими либо участками освещения. Вне рабочего участка спутник находится на свободном участке траектории.

Таким образом, можно выделить три различных режима полета такого спутника:

• •    режим освещения, в котором КА располагает зеркало нужным образом для отражения солнечного света в район освещаемой точки (цели);

• •    режим коррекции, когда зеркало ориентируется так, чтобы сила солнечного давления возвращала аппарат на требуемую орбиту;

• •    режим, когда спутник-осветитель располагает зеркало ребром к Солнцу.

В данной работе использованы результаты, описанные в источнике [4], где рассматривались полярные орбиты с высотами ~4 000 км, которые поворачиваются вслед за Солнцем за счет сил светового давления, аналогично солнечносинхронным орбитам (ССО). Это было возможно, так как КА был оснащен круглым солнечным парусом площадью 785 000 м2, его радиус ~0,5 км. В данной работе, в отличие от источника [4], рассматриваются низкие ССО. При этом поворот орбиты по долготе восходящего узла осуществляется за счет несфе-ричности гравитационного поля, обусловленного полярным сжатием Земли. Радиус зеркала в 10 раз меньше — 50 м. Это делает более реалистичным наведение такого отражателя, так как его конструкция менее инертна [5].

управление параметрами орбиты

Функционал. Как и в работе [4], для реализации управления параметрами орбиты вводится функционал:

Φ = w ₁ ( r _π – r _π *)² + w ₂ ( r _α – r _α *)² + + w ₃ ( i – i *)² + w ₄ (Ω – α ₀ – α ₁ )²,

где (*) — требуемые параметры орбиты, а без (*) — текущие; r _π — радиус перигея (расстояние от центра Земли до перигея орбиты); r _α — радиус апогея (расстояние от центра Земли до апогея орбиты); i — наклонение орбиты; Ω — долгота восходящего узла; α ₀ — долгота Солнца; α ₁ — требуемый угол между долготой Солнца и долготой восходящего узла КА; w_i — весовые коэффициенты.

Алгоритм управления представляет собой следующие три режима:

• 0) режим освещения — непосредственно освещение цели; режим используется, когда спутник находится вне тени Земли и над горизонтом цели;

• 1)    режим коррекции орбиты, когда зеркало располагается нужным образом для возврата траектории к требуемым параметрам;

• 2)    режим с нулевой силой солнечного давления, когда зеркало располагается ребром к Солнцу.

Функционал (1) задает эллипсоид в 5-мерном пространстве. При нахождении спутника вне рабочего участка вводится зона нечувствительности:

• •    при Φ ≥ Φ ₂ = 0,08 спутник переходит в режим коррекции орбиты;

• •    при Φ ≤ Φ ₁ = 0,035 управление переводится в режим с нулевой силой солнечного давления: ( n ^→, s ^→ ) = 0 ( n ^→ — вектор нормали к поверхности зерка- →

ла; s — единичный вектор направления на Солнце).

Локально-оптимальный алгоритм управления. Для того, чтобы сделать текущую орбиту КА близкой к требуемой, достаточно приблизить значение функционала к нулю. Тогда оскулиру-ющие параметры орбиты будут достаточно близки к требуемым значениям. Следовательно, алгоритм управления сводится к отыскани _→ ю вектора силы солнечного давления F , зависящей от на- s _→ правления нормали зеркала n , которая обеспечивает уменьшение значения Φ.

В этом случае направление n ^→ выбирается таким, чтобы значени_.е производной функционала по времени Φ было мини_.-мальным. Предпочтительно, чтобы Φ была меньше нуля — это гарантирует уменьшение функционала и сближение текущей и требуемой орбит, однако в случае положительной производной ее минимум гарантирует слабое нарастание ошибки.

Дифференцируя Φ по времени, получим:

Φ ^. = 2 w ( r – r *) r ^. + 2 w ( r – r *) r ^. + 1 π π π         2 α α α

+ 2 w ₃ ( i – i *)( i ) + 2 w ₄ (Ω – α ₀ – α ₁ ) Ω –

–2 w ₄ (Ω – α ₀ – α ₁ )α ^. ₀ .                    (2)

Анализ производных по времени от оскулирующих параметров орбиты показал, что каждую _→ из _→→→ них можно представить в виде: э ^. = Ψ _эF , где э — од _→ ин из элементов орбиты ( r _π , r _α , i , Ω); F — вектор

→ возмущающей силы; Ψэ — некий вектор изменения соответствующего параметра орбит→ы э. Подробное содержание векторов Ψэ можно найти в работе [4], здесь приведем лишь алгоритм численного расчета компонентов этих векторов. В некой выбранной системе координат рассчитывается изменение элемента орбиты э, вы→званное поочер→едным дейст-в→ием сил F = (1, 0, 0)T; F = (0, 1, 0)T; F = (0, 0, 1)T. В результате каждая→сила задает одну из компонент векторов Ψэ.

Производная функционала по времени (2) может быть представлена в виде:

Φ ^. = Ψ^→ F ^→ – 2 w ₄ (Ω – α ₀ – α ₁ ) α ^. ₀ ,      (3)

где Ψ^→ = 2 w ₁ ( r _π – r _π *)Ψ^→ _π + 2 w ₂ ( r _α – r _α *)Ψ^→ _α +

+ 2 w ₃ ( i – i *) Ψ^→ _i + 2 w ₄ (Ω – α ₀ – α ₁ ) Ψ^→ _Ω .

При решении задачи ограничимся влиянием только второй гармоники разложения гравитационного потенциала Земли, в результате силу, действующую на спутник, можно представить в виде:

→→ →

F = F s + F J ₂,

→     3 µ J R ²

2E где FJ2 = 2 | →r |4

→       →→

[5(re, k)2 re – 2(re, k)k – re] — не- центральная гравитационная поправка к силе тяжести, обусловленная полярным сжатием Земли [6]: µ = 3,986004·105 км3/с2 — геоцентрическая константа гравитационного поля Земли; J2 — 1,082625·10–3 — зональный гармонический коэффициент второй степени; RE = 6 378 км — средний экваториальный радиус Земли; r→ — радиус- в вакууме; m = 500 кг — масса аппа-→ рата; n — вектор нормали зеркала; θ — угол между направлением на Солнце и вектором нормали зеркала (угол между векторами n→ и →s ).

Введем ортонормированный базис _→ в плоскости, натянутой на вектора ^→ s и Ψ, используя алгоритм Грама–Шмидта (рис. 1). Так как сила солнечного давления имеет вид (4), то максимум и минимум скалярного произведени _→ я достигаются только когда вектор F_s лежит в пло _→ скости, образованной векторами ^→ s и Ψ. Для упрощения дальнейших выкладок в качестве первого базисного _→ вектора возьмем нормированный вектор Ψ. Итого имеем:

→     →   → es – s

^→ e ₁ = ^Ψ _Ψ ; ^→ e ₂ = ₁^{1 1}_{– s 12} ; s 1 = (^→ e 1 ^→ s ).     (5)

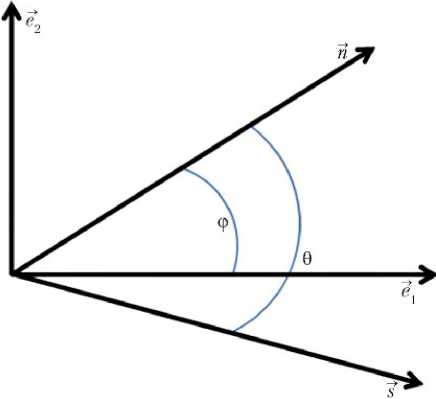
Рис. 1. Введение базиса методом Грама–Шмидта

В полученном базисе (5) нормаль будет иметь следующий вид:

→ n

→ → r вектор точки из центра Земли; re = | →r |

→→

→

n = e ₁ cosϕ + e ₂ sinϕ =

cosϕ sinϕ

^, e

е→диничный вектор, сонаправленный с r→; k — орт направлени→я «Земля – Северный полюс мира»; Fs — сила солнечно- го давления.

Полагается, что происходит полное зеркальное отражение от поверхности паруса. Поэтому сила солнечного давления имеет следующий вид:

F = —2СЛ ^cosQ |cosQ | = s cm                        (4)

= — Fsmax” cos® Icos® I, где С = 1 370 Вт/м2 — солнечная постоянная; A = πR2 = 7,85·103 м2 — площадь зеркала; с = 2,99792·108 м/с — скорость света где ϕ — угол между векторами n→ и →e1, а орт направления на Солнце будет иметь вид:

→ss s =              =

1 s1 es

→ ^→

При коллинеарности s и Ψ в качестве ^→ e ₂ для аналитического расчета берется произвольный _→ вектор, ортогональный ^→ e ₁ .

В случае Ψ = 0 вводится режим управления с нулевой силой солнечного давления (зеркало ребром к Солнцу), а данный базис не строится.

Найдем ϕ, подозрительные на экстремум для производной функционала. по времени

• (3). Возьмем производную от Φ по ϕ:

  →→→→

  
  

  ∂

  
  

  ∂

  
  

  → →→→

  
  

  ∂ → →→→      ∂    →   →→→ →      ∂ → →→→

  
  

  _{д ϕ} Φ    _{д ϕ}(Ψ F – 2 w 4 (Ω – α 0 – α 1 )α 0 ) _{д ϕ}(Ψ F )    _{д ϕ}(( F s + F j 2 )Ψ)    _{д ϕ}(Ψ F s );

  
  

  →

  
  

  F_s Ψ→ min _ϕ ; F_s =– F_{s max}

  
  

  Ψ ^→

  n ( s , n )|( s , n )|; e_x =     => - F _их( n , e_x )( s , n )|( s , n )|^min => ( n , e_x )( s , n )|( s , n )|^ max

  s max ϕϕ

  
  

  Введем обозначение Λ = ( n ^→, e ^→ ₁ )(^→ s , n ^→)|(^→ s , n ^→)|.

  Пусть (^→ s , n ^→) ≥ 0, иначе выберем n ^→: = – n ^→, так как обе стороны паруса считаются зеркальными. Тогда:

  Λ = ( n ^→, e ^→ ₁ ) (^→ s , n ^→)² = cosϕ(( s ₁ e ^→ ₁ – s ₂ e ^→ ₂ )×

  _→      1   _→                     1 1     2 2           ₍₆₎

  ×( e ₁ cosϕ + e ₂ sinϕ))² = cosϕ( s ₁ cosϕ – s ₂ sinϕ)².

  
  

  Производная (6) по ϕ имеет вид:

  
  

  ∂∂

  д Λ = д (cosϕ( s ₁ cosϕ – s ₂ sinϕ)²) =

  = –sinϕ( s ₁ cosϕ – s ₂ sinϕ)²+

  + cosϕ( s ₁ cosϕ – s ₂ sinϕ)2(– s ₁ sinϕ – s ₂ cosϕ).

  ∂

  Λ = 0, следовательно:

  д ϕ

  1) ( s ₁ cosϕ – s ₂ sinϕ) = 0 => n ^→ = ( s ₁ s ₂ ) ^T ⊥ ^→ s ;

  
  

  2) –sinϕ( s ₁ cosϕ – s ₂ sinϕ) + +2cosϕ(– s ₁ sinϕ – s ₂ cosϕ) = 0.

  Разделим на cos²ϕ ≠ 0 ( s ₂ ≠ 0)

  –tgϕ( s ₁ – s ₂ tgϕ) + 2(– s ₁ tgϕ – s ₂ ) = 0;

  tgϕ = t => – t ( s ₁ – s ₂ t ) + 2(– s ₁ t – s ₂ ) = 0;

  s ₂ t ² – 3 s ₁ t – 2 s ₂ = 0;

  
  

  ^t 1,2

  
  

  3 s ₁ ± s ₁ ² – s ₁ ²

  
  

  2 s ₂

  
  

  ϕ ₃

  
  

  3 s – s ² + 8 arctg ^{1      1}      ;

  2 1 – s ₁ ²

  
  

  3 s – s ² + 8

  ϕ = arctg 1     1+

  ⁴              2 1 – s ₁ ²

  ^s

  ϕ = arctg 1;

  s ₁

  ^s

  ϕ = arctg 1+

  ⁶              1 – s ₁ ²

  
  

  → ^→

  При s ₁ = 1, т. е. когда s и Ψ коллинеарны (вырожденный случай), точки, подозрительные на экстремум:

  
  

  ϕ ₁ = 0;  ϕ ₂ = ^π ₂ ;  ϕ ₃ = π;  ϕ ₄ = ³ ₂ ^π .

  
  

  s ₂ = 1 – s ₁ ²;

  
  

  tgϕ =

  
  

  3 s 1    ^ s 2 + 8

  
  

  2 1 – s ₁ ²

  
  

  Имеем для угла ϕ следующие точки, подозрительные на экстремум:

  
  

  ϕ ₁ = arctg

  
  

  3 s 1 + ^ s 2 + 8

  2 1 – s ₁ ²

  
  

  ϕ ₂ = arctg

  
  

  3 s ₁ + s ₁ ² + 8

  2 1 – s ₁ ²

  
  

  + π;

  
  

  Остается только среди значений функционала в этих точках найти наименьшее. Выбор осуществляется программным образом. При этом, если (^→ s , n ^→) < 0, то данное значение ϕ отбраковывается.

  На каждом такте управления рассчитывается оптимальное направление нормали зеркала, которое обеспечивает уменьшение функционала (1), тем самым приближая текущие значения элементов орбиты к заданным.

  Коэффициенты функционала. Для численного моделирования решения задачи подобраны весовые коэффициенты построенного функционала. Выбор коэффициентов осуществлялся по следующему принципу. Добавка к гравитационному полю, обусловленная полярным сжатием Земли, не дает векового ухода радиусам перигея и апогея и наклонению, однако эти значения не остаются постоянными и осциллируют. Величина долготы восходящего узла имеет также колебательный характер. Значение функционала при амплитудном отклонении текущих параметров орбиты от требуемых должно не превышать Φ ₁ . Поэтому величина каждого слагаемого w_i (Δ э )² ≤ Φ ₁ /4. Если взять амплитудное отклонение Δ э , то неравенство превратится в равенство. Таким образом, весовые коэффициенты функционала выбираются

  
  

как обратные квадраты амплитуд элементов орбиты:

w ₁ = w ₂ = 25·10^–11 м^–2;

w ₃ = 2·10⁶ рад^–2;

w ₄ = 1,25·10⁴ рад^–2.

Результаты моделирования. Для верификации предложенной концепции управления таким спутником было проведено математическое моделирование. Траектория спутника рассчитывается на основе уравнений движения в оскули-рующих элементах [7]. При этом положения всех объектов пересчитываются в инерциальную систему координат эпохи t [8].

При моделировании движения КА вокруг Земли с применением управления вводились следующие допущения. Парус считался плоским круглым полотном с двухсторонней отражающей поверхностью. Нормальное световое давление принималось постоянным, поток солнечных лучей — равномерным, но не параллельным: для расчета площади светового пятна на поверхности планеты угловым размером Солнца не пренебре-галось. Гравитационное влияние Луны и Солнца, а также аэродинамическое сопротивление не учитывались. Считалось, что КА обладает массой 500 кг.

Далее приведены результаты математического моделирования поведения параметров орбиты, полученной как одной из наиболее подходящих для освещения Норильска в работах [1–3]. Параметры этой орбиты:

h = 1 335 км; e = 0; Q = 6°; го = 0°; i = 101,1°.

При этом в течение полета также моделировалось освещение Норильска на «рабочих» участках траектории, что обуславливало в значительной мере уход орбиты.

По графикам, представленным на рис. 2, 3, видно, что параметры орбиты достаточно близки к требуемым значениям. Орбита остается солнечно-синхронной в течение всего периода моделирования, составляющего 50 сут. Значения функционала (1) все время превышают Ф 2 , однако это означает, что управление постоянно включено и стремится сократить рассогласование. То, что значение функционала (рис. 3) увеличивается до 4, а потом снижается, связано со следующим. Производная по времени долготы Солнца не постоянна. Следовательно, «красная» линия на графике долготы восходящего узла (рис. 2) не прямая.

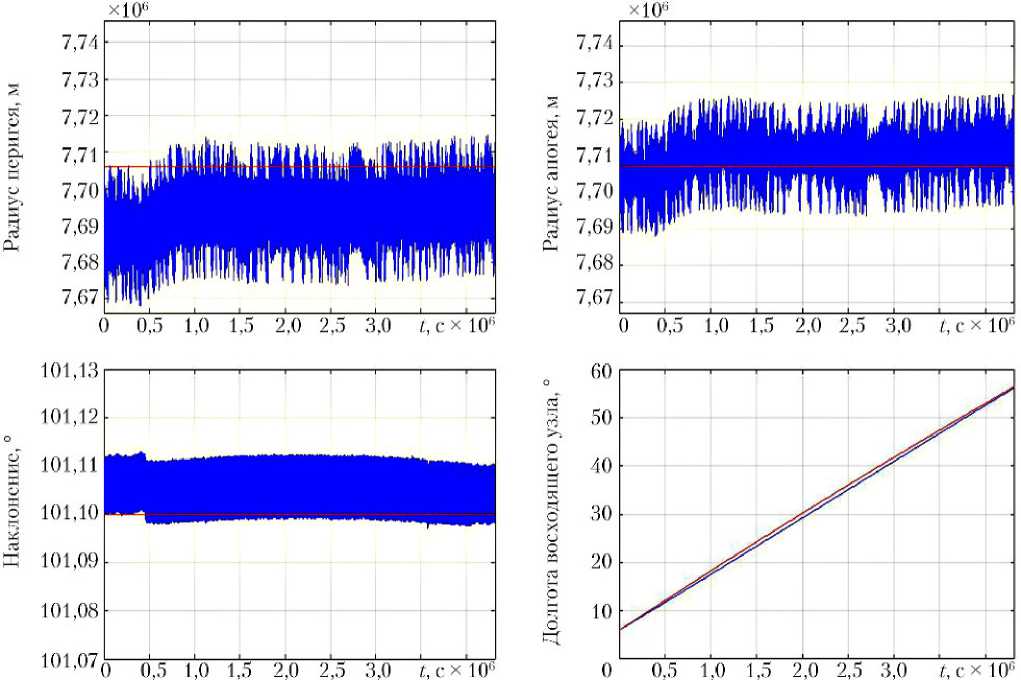
Рис. 2. Оскулирующие параметры «дневной» солнечно-синхронной орбиты при управлении силами солнечного давления на протяжении 50 сут

Отклонение от требуемого значения не превышает 1°. Так как рассогласование не увеличивается, становится очевидным, что управления достаточно для удержания параметров орбиты близкими к требуемым значениям.

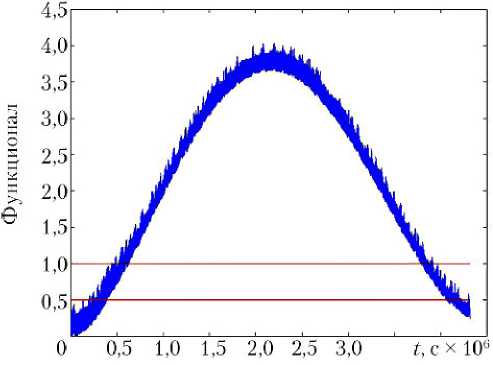
Рис. 3. Поведение функционала

График, представленный на рис. 4, иллюстрирует поведение производной функционала в течение пяти витков. Анализируя его, можно видеть, что производная является непрерывной функцией, что позволяет удостовериться в возможности применения описанного выше алгоритма поиска оптимального направления нормали зеркала.

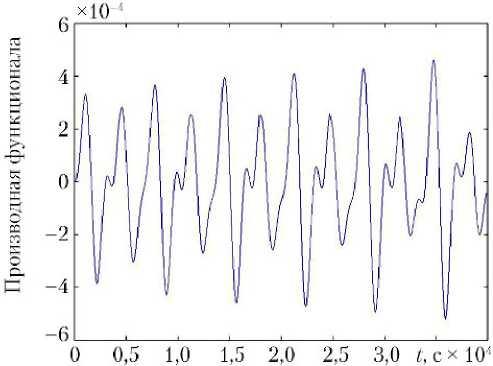
Рис. 4. Производная функционала

Вывод. В данной работе построен алгоритм управления параметрами ССО с использованием силы солнечного давления. Для верификации управления было проведено математическое моделирование поведения параметров орбиты и значения функционала (1). Результаты демонстрируют правильность работы алгоритма.

Выводы из математического моделирования позволяют заключить, что зеркала площадью 7 850 м2 достаточно для удержания параметров орбиты КА массой 500 кг вблизи требуемых значений.

заключение

В работе показана возможность управления элементами орбиты спутника силами светового давления. Предложенный метод управления элементами орбиты позволяет удерживать их вблизи заданных значений. Ввиду того, что в качестве управляющего воздействия используется сила солнечного давления, управление орбитой КА происходит без затрат топлива, являющегося дорогим и ограниченным ресурсом на борту КА. В результате использование солнечного паруса позволяет увеличить срок эксплуатации спутника.

Также сделан вывод, что выбранной площади отражателя недостаточно для систематического изменения долготы восходящего узла, а хватает только для коррекции ее значения.

Предложенный в работе метод может быть использован не только для коррекции орбит спутников-осветителей, но и для создания больших апертур в околоземном космическом пространстве.

В качестве продолжения работы планируется изучить функционал, содержащий большую полуось и эксцентриситет орбиты вместо радиусов апогея и перигея. Это позволит более точно и наглядно отслеживать параметры орбиты.

Работа проводилась при частичной финансовой поддержке РФФИ по грантам № 170801635 и № 180801379.