Управление роботом-манипулятором при смене топливных баков двигательной установки геостационарного спутника

В связи с возросшими требованиями к глобальности, скорости и объемам информационного обмена в настоящее время многие страны приступили к реализации низкоорбитальных спутниковых систем связи, состоящих из тысяч мини-спутников на орбитах высотой от 500 до 1600 км. Достойный ответ традиционной космической связи на основе геостационарных платформ противостоит этим вызовам. Такие перспективные платформы собираются на геостационарной орбите (ГСО) космическими роботами-манипуляторами (КРМ) из сменных и пополняемых компонентов, а затем регулярно обслуживаются КРМ в течение нескольких десятилетий.

Традиционные геостационарные спутники связи (ГСС) имеют гарантированный срок службы до 15 лет. При продлении срока службы

ГСС важнейшей является проблема дозаправки топливом их электрореактивных двигательных установок (ЭДУ). В системе управления движением (СУД) КРМ применяются исполнительные органы в виде кластера гиродинов (ГД) – двухстепенных силовых гироскопов и ЭДУ на основе как плазменных, так и каталитических электро-реактивных двигателей (ЭРД) [1,2]. В штатном режиме СУД измерение координат движения космического аппарата (КА) выполняется бес-платформенной инерциальной навигационной системой (БИНС) с коррекцией сигналами от навигационных спутников GPS/ ГЛОНАСС и звездных датчиков.

В статье рассматриваются вопросы управления КРМ при дозаправке ЭДУ на основе смены топливных баков. Предлагается стратегия и разрабатываются методы управления КРМ в этом режиме при одновременной стабилизации углового движения механической связки КРМ с ГСС. Определяются требования к электромеханическим приводам робота-манипулятора и представляются результаты компьютерной имитации динамических процессов.

ОПИСАНИЕ ЗАДАЧИ И СТРАТЕГИЯ УПРАВЛЕНИЯ

Рассматривается задача управления КРМ при смене топливных баков двигательной установки ГСС. Предполагается, что КРМ и ГСС жестко состыкованы, а механические манипуляции с баками происходят в автоматическом режиме. Концевое звено манипулятора содержит специальный механизм – ключ, который при замыкании жестко удерживает очередной топливный бак.

Целями исследования являются: анализ стратегии управления – последовательности действий манипулятора при захвате/освобож-дении баков и их перемещениях в заданные положения; выбор кинематической схемы манипулятора, числа его звеньев, их геометрических и инерционных характеристик, а также параметров электромеханических приводов; расчет рабочей зоны манипулятора; оценка динамических характеристик СУД при угловой стабилизации связки КРМ и ГСС в процессе смены баков. Компоновка жесткой сцепки КРМ с ГСС, для компактности без отображения панелей солнечных батарей (СБ), представлена на рис. 1, где все размеры указаны в метрах.

На рисунке 1 приведены используемые формы и размеры компонентов механической связки: корпус КРМ – цилиндр диаметром 1 м и длиной 2.5 м с установленными на нем манипулятором и контейнерами с баками, частично вы- ступающими за его обвод; корпус ГСС – цилиндр диаметром 1.1 м и длиной 2.7 м. Было принято, что каждый сменный топливный бак имеет размеры 0.4 х 0.4 х 0.5 м, объем 80 литров, масса полного бака равна 90 кг, а пустого бака – 10 кг. При выбранных геометрических параметрах на каждой из двух продольных сторон корпуса КРМ допускается размещение до пяти контейнеров. Для начала последовательности смены топливных баков один из контейнеров в корпусе КРМ должен быть пустым, см. например, контейнер a на рис. 1.

На рисунке 2 представлена кинематическая схема бортового манипулятора антропоморфной структуры с 4 звеньями ( i = 1,2,...4 = 1 ^ 4 ) и 6 степенями свободы, которым соответствуют угловые координаты q s , s = 1 ^ 6. Здесь указаны концы звеньев манипулятора в точках А , B , C и концевая точка D ключа замкового механиз-

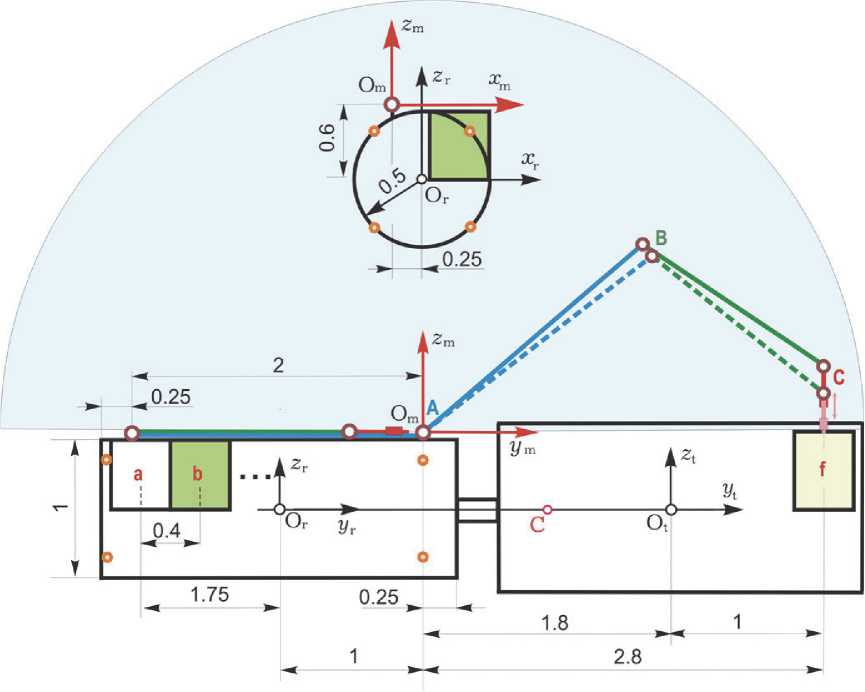
Рис. 1. Схема управления манипулятором и его рабочая зона при смене топливных баков

+

Рис 2. Кинематическая схема манипулятора

ма. В точках А и С применяются двухстепенные шарниры, которые однозначно формализуются двумя стандартными одноосными шарнирами при значениях длины фиктивных звеньев 1 ₀₁ = 1 ₀₃ = о, см. рис. 2. Последний шарнир обеспечивает вращение ключа открытия/закрытия замка вокруг продольной оси бака, а остальные – совмещение точки С манипулятора с заданной в рабочей зоне при произвольной ориентации последнего звена.

Манипулятор закреплен на корпусе КРМ стойкой (master) в точке O _m системы координат O _m x _m y _m z _m , которая фиксирована в системе координат O r x _r y _r z _r , связанной с корпусом КРМ (robot) в его центре масс O _r , см. рис. 1. Захват бака достигается перемещением ключа по нормали к плоскости крышки бака (см. рис. 1) с последующим его поворотом на угол п /2.

Применяемая стратегия смены топливных баков ЭДУ использует такие положения:

• 1)    пустые баки поочередно перемещаются манипулятором из контейнеров ГСС в контейнеры КРМ, а заполненные топливом баки – наоборот, из контейнеров КРМ в контейнеры ГСС;

• 2)    установка баков в контейнеры завершается их автоматической механической фиксацией;

• 3)    включение /отключение системы подачи топлива от каждого бака к ЭДУ осуществляется роботизированным мехатронным модулем, встроенным в каждый контейнер ГСС.

МАТЕМАТИЧЕСКИЕ МОДЕЛИ И ПОСТАНОВКА ЗАДАЧИ

При описании движения механической связки КРМ с ГСС применяются (i) экваториальная инерциальная системы координат (ИСК)

I _е с началом в центре Земли O _e , (ii) связанная система координат (ССК) B (О xyz ) с началом в полюсе O , которая совпадает с системой координат O _r x _r y _r z _r , КРМ (iii) орбитальная система координат (ОСК) O (O x ^o y ^o z °) с началом в полюсе O и ортами r^o , т^о , n ^o , которая имеет следующие направления осей и ортов: ось O x ^о направлена по радиали r^o , ось O z ^о - по нормали no к плоскости орбиты, а ось O y ^о - по трансверсали т ^о и направлена в сторону орбитального движения, см. рис 1, где представлена также система координат O _t x _t y _t z _t , связанная с корпусом ГСС (цель, target) в его центре масс O _t .

Далее используются общепринятые обозначения col( - ) = { • } , line( - ) = [ • ] , GO, М, ( • ) , [ a x ] и ° для векторов, матриц и кватернионов, матриц [ a ] i стандартного элементарного поворота вокруг i -ой оси на угол a , i = 1 ^ 3 , а также C _a = cos a , S _a = sin a .

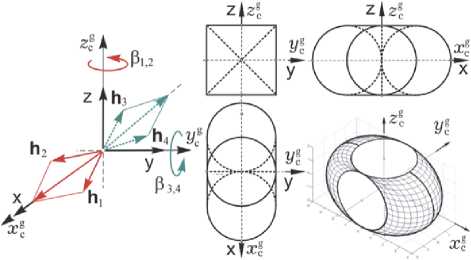
Рис. 3. Схема СГК и область вариации его КМ

Для управления ориентацией связки КРМ с ГСС применяется силовой гироскопический кластер (СГК) на основе четырех ГД по схеме 2-SPE с ортами векторов кинетических момен тов (КМ) hp (вp), p = 1 ^ 4, см. рис. 3, где приведена также область вариации нормирован- ного вектора КМ h(p) = Sh p (в p) кластера со столбцом Р = {Рp} и ее проекции на плоскости базиса Oxgygzg. Применяемый явный аналитический закон настройки СГК (распределения трехмерного вектора его управляющего момента Мg = {Мg} между четырьмя ГД) позволяет исключить избыточность данного кластера с вектором кинетического момента H = hgh(P), где hg - одинаковое для всех четырех ГД постоянное значение модуля собственного КМ.

Ориентация ССК B в ИСК I _@ определяется кватернионом Л = ( X₀, X ) , где X = { X i } , вектором модифицированных параметров Родрига (МПР) ст = { о i } = e g ( Ф /4) с ортом e оси Эйлера и углом Φ собственного поворота.

В ИСК I _@ кинематические уравнения для вектора r _o расположения КРМ, кватерниона Л и вектора МПР ^σ имеют вид

г0 = г' + ®х г0;    Л = Л ° ®/2;

о= ^(1 -о2)го+ 2 охш+2(0, ю)о, где вектор ω представляет абсолютную угловую скорость корпуса КРМ и используется обозначение (•)‘ локальной производной по времени. Кватернион Лo ориентации базиса O относительно базиса Iе определяется

A ° ° o/T уравнением Л = Л ° ю/2, углами рыскания ф1 = v, крена ф2 = Ф и тангажа ф3 = 0 в последовательности 132, а также матрицей направляющих косинусов координатного перехода от ОСК к ССК C0 = [ф2]2 [ф3]3 [ф1]1. В свою очередь, погрешность ориентации базиса B в орбитальном базисе O определяется кватернионом E = Л0 ° Л- (e0,e), где e0 = Cфс/2, e = Sфe/2ee с ортом оси Эйлера ee и углом ошибки Фе, матрицей Ce = I3 - 2[ex]Qe, где Qe = I3 e0 + [ex], вектором угловой погрешности 5ф = {5фi} = {2e0ei} и вектором МПР Oe = {о®} = ee tg(Фe /4). При этом вектор Sto погрешности угловой скорости определяется как Sto = to - Ceto0 (t).

При моделировании движения связки КРМ с ГСС применяется векторная форма классических уравнений Эйлера-Лагранжа [3].

В ССК Oxyz с полюсом O векторы рi, i = 1 ^ 4 определяют положения центров масс ci звеньев манипулятора с массами mi и собственными тензорами инерции Jic, а векторы рг = 0 и рt - положения центров масс Or и Ot робота (индекс r) и цели (индекс t) с массами и собственными тензорами инерции mr, Jc и mt, Jc соответственно. Положение центра масс C связки КРМ и ГСС (робот, манипулятор с 4 звеньями и цель, см. рис. 1) суммарной мас- сы

P c

m = m_r + Z m i + m_t определяется вектором

= { x _c, У _c, z _c} по соотношению

L - m Pc = mr Pr +Zm i pi + mt Pt, где введен вектор статического момента Тензор инерции J механической системы в люсе O вычисляется по соотношению

L .

по-

j - и_$ | = j 0 + z j 0 + j 0 , где при единичном тензоре E

J 0 = J c ; J 0 = J c + m i ( E P t P i - P i P i ) ;

J ° = J? + mt (E pt p,-p,p *).

При векторе v _o скорости полюса O поступательное движение связки КРМ с ГСС описывается векторным уравнением

mv° -Lхю = юх(Lхю)

-E,(m(2toxp‘ + p’)) + Pe + Fgr,    (2)

где v ° = v ° +®^x v ° ; p‘ = ² s ^{(( d}p , ^{/ d} q s ⁾ q s ⁾ ;

p>2 s ((dp,/d qs) qs + 2 k (d2 p,/d qk d qs)), векторы Pe и Fgr представляют силы тяги ЭДУ, центрированной в полюсе O , и гравитации.

Через ω _i обозначим вектор угловой скорости i -го звена манипулятора в ССК. Производная этого вектора по времени имеет вид (to i = to i + to x to i . В ССК O xyz с полюсом O вращательное движение связки указанных твердых тел описывается векторным уравнением

L x v ° + Jto = -L x (юх v°)

-юх(Jrn+H) -R + Mg + Me + Mgr, (3)

где

R = Z i ( J 0 to i + to x J 0 ®. + to i x J 0 ( to + to i )

⁺ m i - P i - ^{x ( to x ( to x} P i -) + ^{2 to x} P i + P i ")

^, векторы M^g = - H ‘ и M^e - M представляют управляющие моменты СГК с вектором КМ H и ЭДУ на основе 8 каталитических ЭРД, а вектор M ^gr - гравитационный момент.

Векторные уравнения Эйлера (2), (3) дополняются стандартными уравнениями Лагранжа по степеням подвижности q_s манипулятора, где в правых частях наряду с обобщенными силами Q_s , представляющими моменты электромеханических приводов, имеются механические моменты [3], которые обусловлены пространственным движением связки КРМ с ГСС.

При цифровом управлении u g (t ) = {u g, _g ( t )} СГК с периодом T u , где для k е N₀ - [0,1,2,...) компоненты ^u g_t ⁽ t ⁾ = ^up_k V t е [ t_k ^, t_k J, t k + 1 = t k + T u формируют вектор управляющего момента СГК

■

M k ( t ) = - h g A h ( в ( t ) u k ( t ) ; в ( t ) = u k ( t ) , (4)

где матрица Якоби A _h ( в ) = Э М ( в ) /дР .

В процессе угловой стабилизации связки КРМ с ГСС в ОСК при законе наведения Л°(t), to°(t), to 0(t) = E0(t) после дискретной фильтрации измеренных значений вектора углового рассогласования £ a =-5ф l, l е N0 с периодом T = T /4 формируются значения вектора 8kf, k е N 0, которые применяются в алгоритме управления СГК с периодом Tu в виде а a a a af ~ a a a af

gk+i = в gk + c ek; mk = к (gk + p 8k);Mk = юk х Gk + J(Ckeg + [Ckto>]tok + mk). (5)

Здесь вектор Gk =Jωk + Hk и используются постоянные диагональные матрицы Ka, Ba, Ca и Pa. Далее вектор Mk с помощью явного закона распределения команд между четырьмя ГД [4] «пересчитывается» в столбец uf = {и®.} командных сигналов управления гиродинами, которые фиксируются на полуинтервалах цифрового управления СГК с периодом Tu при формировании его управляющего момента Mk (t) по соотношениям (4).

В статье решаются следующие задачи:

• (i)    обоснование кинематической схемы, параметров манипулятора и его рабочей зоны;

• (ii)    синтез законов наведения схвата манипулятора;

• (iii)    оценка потребных характеристик электромеханических приводов манипулятора;

• (iv)    компьютерный анализ динамики СУД при смене топливных баков ЭДУ.

ПАРАМЕТРЫ МАНИПУЛЯТОРА И ЕГО РАБОЧАЯ ЗОНА

Будем считать, что начало O _m системы координат (СК) манипулятора O _m x _m y _m z _m определяется вектором r _m = { — 0.2, — 1, — 0.6} м в СК O r x _r y _r z _r корпуса КРМ, см. рис. 1, где также показаны контейнеры a (пустой) и b c центрами крышек {0.55, - 1.75, - 0.1} м и {0.55, - 1.35, - 0.1} м, соответственно. Здесь центры крышек баков лежат в одной плоскости, т.е. рабочая зона манипулятора должна располагается над плоскостью крышек ( z _m >  0 ) и в ней не должно быть мешающих элементов конструкции КРМ и ГСС.

Положение центра масс ГСС относительно полюса O определяется вектором p _t = {0, 2.8, 0} м. Пустой (заменяемый) бак f в системе координат ГСС O _t x _t y _t z _t имеет координаты центра крышки {0,1,0} м. Расстояние от контейнера a КРМ до бака в контейнере f ГСС составляет 5.6 м. Из простых геометрических расчетов следует, что для суммы длин первых двух звеньев манипулятора должно выполняться условие 1 1 + l 2 >  3.3 м. Этим условиям удовлетворяет манипулятор с кинематической схемой на рис. 2 при длинах звеньев

• 1 1 = 2 м, l ₂ = 1.5 м, l ₃ = 0.5 м, когда 1 ₄ = 0 (без бака) и 1 ₄ = 0.25 м (с баком), и с рабочей зоной в виде полусферы с радиусом 3 м, выделенной на рис. 1 голубым цветом, при следующих ограничениях на угловые координаты:

• - П < q1 < П, 0 < q2 < п;

• -п< q i <п , i = 3 ^ 6.         (6)

С каждым i -ым ( i = 1 ^ 4 ) звеном связывается СК с началом в точке сопряжения i -ой пары звеньев, см. рис. 2. Кинематическая модель манипулятора обязательно включает формулы решения прямой и обратной задачи кинематики [5].

Прямая задача состоит в расчете векторов декартовых координат r ( q ) , линейных скоростей v ( q , q ) и ускорений w ⁽ q , q , ^{q )} заданных точек в кинематической цепи манипулятора, а также кватернионов либо матриц ориентации, в системе координат манипулятора O _m x _m y _m z _m при заданных значениях векторов угловых координат q = { q s }, s = 1 ^ 6, скоростей q и ускорений q звеньев. Для решения прямой задачи кинематики используется обратный рекуррентный переход из i -ой в ( i — 1) -ую СК, начиная с последнего звена до стойки при i = 1 [6].

Обратная задача кинематики манипулятора состоит в определении вектора угловых координат q = { q_s } по заданным декартовым координатам вектора r _D = { x _D , y _D , z _D } точки D схвата и ориентации СК последнего звена манипулятора относительно СК O _m x _m y _m z _m стойки (master) при ограничениях (6). В общем случае решение обратной задачи неоднозначно. Для схемы на рис. 2 единственное решение этой задачи получается однозначно при наличии возможности перемещения звена 3 с точкой D в отрицательном направлении оси O _m z _m , см. рис. 1.

ЗАКОНЫ НАВЕДЕНИЯ СХВАТА И УПРАВЛЕНИЯ ПРИВОДАМИ

Синтез законов программного наведения схвата манипулятора при переходах между целевыми состояниями с краевым условиям по каждой из угловых координат q_s включает два аспекта: (i) расчет значений времени начала t i (initial), завершения t _f (final) и длительности T_m = t _f — t i выполнения каждого этапа и (ii) формирование временных зависимостей углов q_s ( t ) , скоростей q _s ( t ) и ускорений q_s ( t ) при ограничениях на углы (6), а также на модули скоростей и ускорений

I <7 s ⁽ t ) 1 ^ <7 *, I ^q s ⁽ t ) ^ 4 ^ t e T m = [ t i , t f ] (7) при заданных значениях параметров q * и q* . Здесь каждый из последовательных этапов перемещения включает стандартные участки разгона, движения с постоянной скоростью и торможения.

При цифровом управлении редукторными электроприводами по степеням подвижности манипулятора применятся адаптивно-робастные алгоритмы с эталонной моделью наведения [7].

ОЦЕНКА МОМЕНТНЫХ СВОЙСТВ ПРИВОДОВ МАНИПУЛЯТОРА

Для простейшей оценки потребных моментных характеристик электромеханических приводов вычисляются обобщенные силы – кру- тящие моменты на выходных валах приводов манипулятора, когда их нагрузка представлена только обобщенными силами инерции при движении звеньев, а разнообразные моменты сил сопротивления такому движению не учитываются. В этом случае обобщенные силы Q = Q(t) вычисляются по соотношению

^{Q (} t ⁾ = A ⁽ q ( t ⁾⁾ q ( t ⁾ + b ( q ( t ^{), q} ( t ^)), (8)

где A ( q ) = A ( q ( t ) — симметричная матрица инерции и b ( q ( t ), q ( t ) - вектор центробежных и кориолиссовых сил, приведенных к выходным валам приводов в шарнирах манипулятора.

АНАЛИЗ ДИНАМИКИ СИСТЕМЫ УПРАВЛЕНИЯ ДВИЖЕНИЕМ

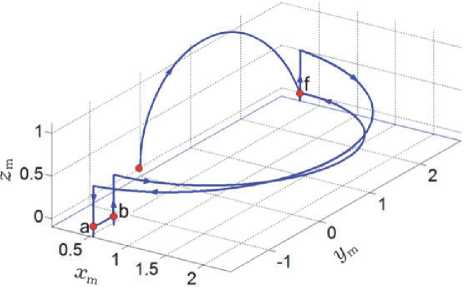
Рис. 4. Траектория схвата манипулятора при замене первого топливного бака ЭДУ

Анализ динамики СУД при смене топливных баков ЭДУ выполнен на основе методов и средств компьютерной имитации для следующих значений инерционных параметров меха- нической системы твердых тел:

т _г = 2800 кг; J ° = 10³ diag{5,3,4}кгм²;

m _t = 3500 кг; J } = 10³ diag{20,18,13}KrM²; массы первых трёх звеньев манипулятора равны 50, 35 и 15 кг; масса 4-го звена составляет 10 кг (с пустым баком) или 90 кг (с заполненным баком), а сцепка КРМ и ГСС со всеми топливными баками имеет массу m = 6800 кг.

Было принято, что период цифрового управления СГК T u = 4 с, каждый ГД имеет собственный КМ h _g = 30 Нмс, а ограничения для приводов манипулятора таковы: q * = 0.025c^-1; q* = 0.0125c - ².

При смене баков манипулятор выполняет типовые действия, поэтому далее кратко приводятся результаты компьютерной имитации замены только первого топливного бака, когда

• 1)    схват переводится из транспортного положения r_D = { x _D , y _D , z _D } = {0,0,0} сначала к контейнеру ГСС с пустым баком f (см. рис. 4), который затем перемещается в пустой контейнер a КРМ;

• 2)    схват переходит к контейнеру b КРМ и далее перемещает полный бак b в контейнер f ГСС.

Декартовые координаты целевых точек рабочей зоны манипулятора в его системе координат O _m x _m y _m z _m и последовательность действий во времени представлены в табл. 1.

На рисунках 5 и 6 представлены изменения угловых координат звеньев манипулятора и оценки соответствующих им потребных моментов на выходных валах приводов при замене первого топливного бака. При использовании редукторов с передаточным отношением

Таблица 1. Состояния манипулятора, координаты схвата, время выполнения этапов и их длительность

№	Последовательность состояний манипулятора и положения хвата	Координаты схвата при завершении этапа, м			Отметки времени и длительность, с
		x D	У D	z D	t i	t f	T m
1	Развертывание, переход к баку f и зависание	0.25	2.8	0	0	102	102
2	Вставка ключа в пустой бак f ГСС	0.25	2.8	- 0.1	102	108	6
3	Закрытие замка и захват бака f	0.25	2.8	- 0.1	108	175	67
4	Вытягивание бака f из контейнера f ГСС	0.25	2.8	0.25	175	186	11
5	Бак f выведен из контейнера f ГСС	0.25	2.8	0.5	186	195	9
6	Переход к баку а КРМ и зависание	0.25	- 1.75	0.5	195	309	114
7	Вставка бака f в контейнер а	0.55	- 1.75	- 0.1	309	333	24
8	Открытие замка бака f в контейнере а КРМ	0.55	- 1.75	- 0.1	333	384	51
9	Зависание над контейнером а КРМ	0.55	- 1.75	0	384	391	7
10	Переход к баку b КРМ и зависание	0.55	- 1.35	0	391	405	14
11	Вставка ключа и захват бака b КРМ	0.55	- 1.35	- 0.1	405	476	71
12	Вытягивание бака b из контейнера b КРМ	0.55	- 1.35	0.5	476	503	27
13	Переход к контейнеру f ГСС и зависание	0.25	2.8	0	503	614	111
14	Вставка бака b в контейнер f ГСС	0.25	2.8	- 0.1	614	725	111

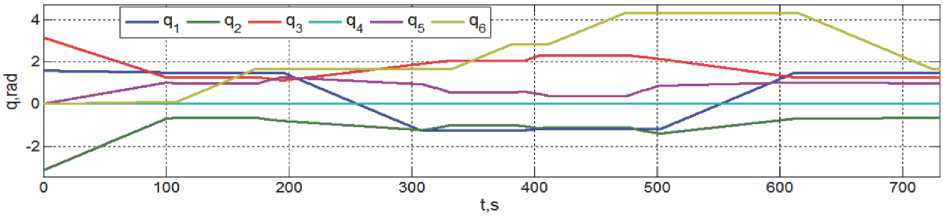
Рис. 5. Изменение угловых координат манипулятора при замене первого топливного бака

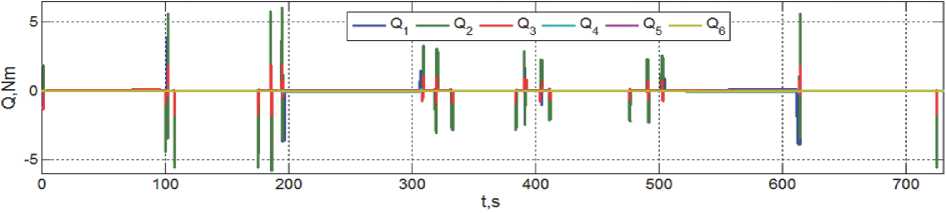
Рис. 6. Оценки потребных моментов на выходных валах приводов манипулятора

О           100          200          300          400          500          600          700

t, s

Рис. 7. Угловое отклонение ССК относительно OCK при смене топливного бака

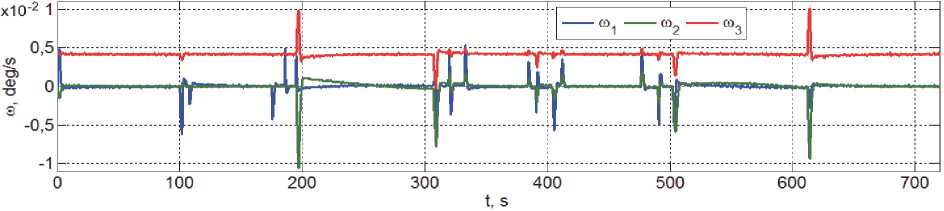
Рис. 8. Изменение вектора угловой скорости связки КРМ и ГСС при смене бака

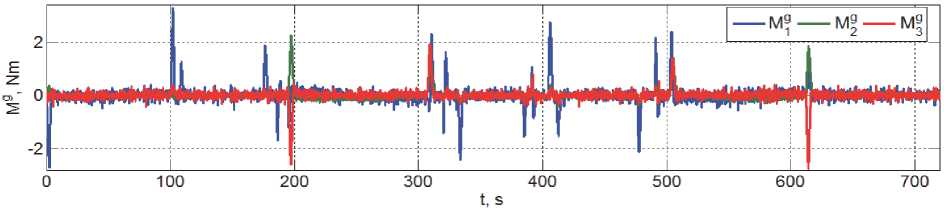
Рис. 9. Управляющий момент силового гироскопического кластера при смене бака

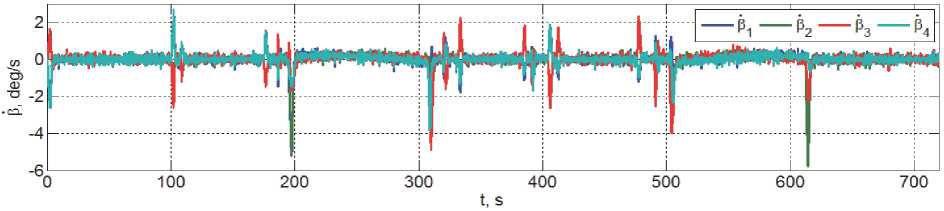
Рис. 10. Изменения угловых скоростей гиродинов при смене топливного бака

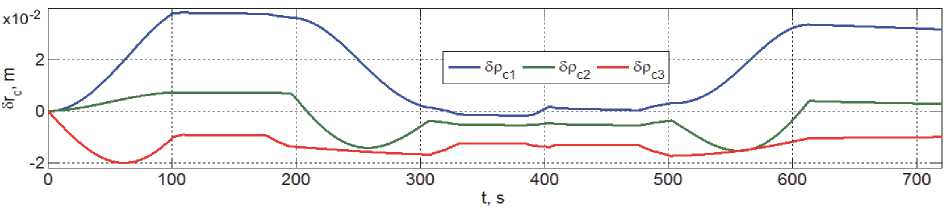
Рис. 11. Изменение вектора положения центра масс связки КРМ и ГСС при смене бака

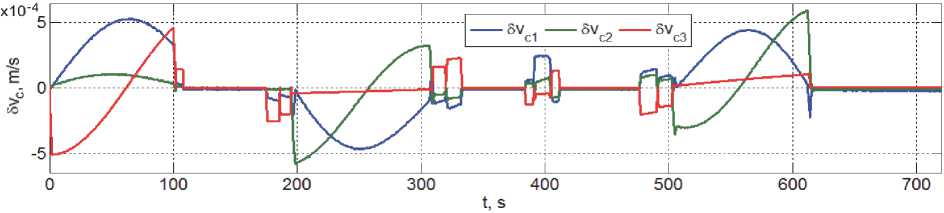
Рис. 12. Изменение вектора скорости центра масс связки КРМ и ГСС при смене бака

1:400 потребные моменты с учетом возможных потерь не превысят 10 Нм, что позволяет использовать шаговые двигатели с номинальным моментом 0.025 Нм и максимальной скоростью 100 об/мин.

Изменения кинематических параметров ориентации связки КРМ и ГСС относительно OСК при смене бака приведены на рис. 7 и 8, а соответствующие изменения вектора управляющего момента СГК и угловых скоростей гиро-динов – на рис. 9 и 10.

Наконец, на рисунках 11 и 12 представлены изменения векторов положения и скорости поступательного движения центра масс связки КРМ и ГСС при смене бака.

ЗАКЛЮЧЕНИЕ

Кратко представлены стратегия и методы управления космическим роботом-манипулятором при смене топливных баков электро-реактивной двигательной установки геостационарного спутника связи. Для конкретных исходных данных установлены требования к электромеханическим приводам манипулятора и представлены результаты компьютерной имитации динамических процессов при смене топливных баков с одновременной угловой стабилизацией механической связки робота и геостационарного спутника в орбитальной системе координат.