Управление с обратной связью в классической системе типа «хищник-жертва»

Нелинейные модели популяционной динамики, предложенные в работах Лотки и Вольтерра [7, 10], к настоящему времени получили самое широкое распространение. Их разнообразные обобщения нашли применение не только в биологии, но и в медицине, экономике, социальных науках. Особый интерес представляют задачи управления в подобных системах. Здесь можно отметить следующие работы,

Русаков Сергей Владимирович, д.ф.-м.н., профессор кафедры прикладной математики и информатики, Пермь

Чирков Михаил Владимирович, аспирант кафедры прикладной математики и информатики, Пермь посвященные использованию системы «хищник–жертва» в различных областях. Обобщение модели Лотки–Вольтерра для описания взаимодействия одновалентных антител с размножающимся одновалентным антигеном предложено в работе [6]. Исследование поведения траекторий этой модели проведено в работах [8, 9], где показано, что в рассматриваемой модели существуют устойчивые периодические решения малой и большой амплитуды, а также приведена биологическая интерпретация полученных результатов. В работе [4] рассматривается оптимальное дискретное управление в системе «хищник–жертва», предложенный алгоритм основан на сведении нелинейной системы к кусочно-линейной, для построения управляющей функции решается классическая задача линейного программирования. Показано, что описанный алгоритм позволяет приводить нелинейную систему Лотки–Вольтерра в состояние равновесия. Применение системы «хищник–жертва» в социальных процессах анализируется в работе [2]. В монографии [3] решен целый ряд задач по стабилизации и управлению в экосистемах, имеется обширная библиография по исследуемой проблематике. В работе [5] предложен и исследован алгоритм управления с обратной связью системой типа «хищник–жертва».

В технических системах, рассматриваемых как «черный (серый, белый) ящик», популярным способом управления с обратной связью является использование так называемых ПИД-регуляторов (пропорциональных, интегральных, дифференциальных), позволяющих перевести систему из одного состояния в другое. Применение этой «технологии управления» к системам типа популяционной динамики практически не исследовано.

Настоящая работа посвящена изучению классической системы типа «хищник– жертва», для которой имеет место нетривиальная особая точка типа «центр». Выбор авторами этой модели обусловлен двумя моментами: с одной стороны, она является достаточно типичным представителем класса моделей популяционной динамики, с другой – имеет достаточно простую структуру и небольшое число параметров, что позволяет провести ее детальное аналитическое исследование. Поставлена задача управления этой системой, обеспечивающего ее перевод в устойчивое стационарное состояние и реализуемого с помощью ПИД-регулятора. Кроме того, предложен алгоритм идентификации параметров данной системы, базирующийся на результатах управления ею.

Постановка задачи

Рассмотрим следующую задачу управления для классической системы типа «хищник–жертва» [3]:

X = a 1 X - в 1 XY + U ( t , X , Y ), Y = - a 2 Y + k в 1 XY , t >  0,

0 <  k <  1, a 1 , в 1 , a₂ >  0, X (0) = X 0 , Y (0) = Y o , X 0 , Y o >  0.

Будем полагать, что значения параметров задачи (1)–(2) нам неизвестны, но значения функций X ( t ) и Y ( t ) могут быть получены (измерены) в любой момент времени с необходимой точностью (кибернетическая модель «белый ящик»), а управление U ( t , X , Y ) означает возможность добавлять (убавлять) в систему извне любое необходимое количество «жертвы».

Цель управления – обеспечить асимптотическую стабилизацию функции Y ( t ) около заданного значения:

Y ( t ) — --- > A = const > 0.

V 7 t ^^

Проведем обезразмеривание задачи (1)–(2), выбрав в качестве характерного значения и «хищника», и «жертвы» величину A , а характерного времени - величину A t = а 21 ; сохраняя прежнее обозначение для времени, получим

x = а х - в xy + u ( t , x , y ), y = - y + k в xy ,

где

0 <  k <  1, а, в >  0,

x ⁽⁰⁾ = x ₀, y ⁽0) = y o , x o , y о >  0,

y ( t ) ——^ 1,                             (6)

α        β                   U ( t , X , Y )

а = —, в = ~ A , u ( t , x , y ) =--------- .

^α 2        ^α 2                    ^α 2 ^A

Для начала проанализируем вариант u ( t , x , y ) = const с помощью первого метода Ляпунова. Нетрудно установить, что в этом случае нетривиальным стационарным решением задачи (4)–(5) является

_    1        _          - 1 I x * = —,  y * = 1, u * = — 1

k в                k (

-

α

и корни соответствующего характеристического уравнения равны

^ 1,2 =

а - в

± Dd ,

D =

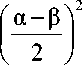
- в

При а < в это решение является устойчивым узлом в случае D >  0 и устойчивым фокусом при D <  0. В случае а >  в имеем соответственно неустойчивый узел и неустойчивый фокус. Таким образом, в этом варианте устойчивое решение получится только в случае выполнения условия α < β .

Управление с помощью ПИД-регулятора

Поскольку параметры системы (1) нам неизвестны, достижение цели управления (3) возможно только при использовании алгоритмов управления с обратной связью. Для реализации такого алгоритма рассмотрим управляющую функцию в виде ПИД-регулятора, широко используемого при управлении в различных технических системах (см. например [1]):

t

u ( t , x , y ) = K П • e ( y ) + K И j e (t) d т + K д • e ? ( y ), K _n, K и , K д , = const,          (10)

где e(y ) - функция рассогласования; e ( y ) = 1 - y ( t ).

Для исследования устойчивости системы (4) с управлением вида (10) методом Ляпунова предварительно преобразуем ее, продифференцировав первое уравнение:

x = z, z = (a - вy)z + вxy(1 — kвx) + u(t, x, y, z),(11)

y = - y + k вxy, где ui (t, x, y, z) = - y (1 - kвx)(-K П + KД (1 - kвx)) + K И (1 - y) - K д kв zy.(12)

Соответствующее характеристическое уравнение имеет вид

X3 + a1k2 + a 2X + a 3 = 0,(13)

где a1 = в(1 + KДk) - a, a2 = в(1 + KПk), a3 = KИkв.(14)

Воспользуемся критерием Рауса–Гурвица, согласно которому все корни характеристического уравнения (13) имеют отрицательную действительную часть тогда и только тогда, когда выполняются условия

T = a 1 = в(1 + K _Д k ) - a >  0,

T =

1 2

a ₁

a ₃

a ₂

= a 1 a ₂ - a ₃ = (в(1 + K _Д k ) - а)в(1 + K _П k ) - K И k в >  0.

Нетрудно показать, что следствием соотношений (15) являются ограничения

Д

1 1 a

-

k ( в

¹ = ^K Д * ,

K _и <  |(в(1 + K д k ) - a)(1 + K n k ) = K И .                     (17)

Таким образом, основное функциональное назначение составных частей (слагаемых) ПИД-регулятора заключается в следующем:

– «дифференциальная» составляющая обеспечивает устойчивость управления в случае α > β (условие (16));

– «интегральное» слагаемое дает необходимое значение величины управления

t

К и J e (t) d т t ^„ >  u *                               (18)

и должно удовлетворять условию (17);

– «пропорциональная» составляющая позволяет регулировать скорость выхода на стационарное решение.

Полученные результаты иллюстрируются на рисунке, где приведены данные расчетов для некоторых наборов параметров. Во всех случаях параметры модели имели значения a = 2, в = 1, k = 0,8, начальные условия x ₀ = 1, y ₀ = 0,8. Варьировались коэффициенты ПИД-регулятора. Рассматриваются четыре варианта, здесь же приведены значения критериев (16)–(17) и собственные значения соответствующего уравнения (13):

* 77 ‘(Д ‘X ‘1>1 \1>X ‘^X               * И W ‘X ‘v)?7 \М ‘^Х                 * 77 ‘(.Л ‘X ‘^П \^£ \^Х                * 77 ‘(^ ‘X ‘^П ‘(^Л \^Х

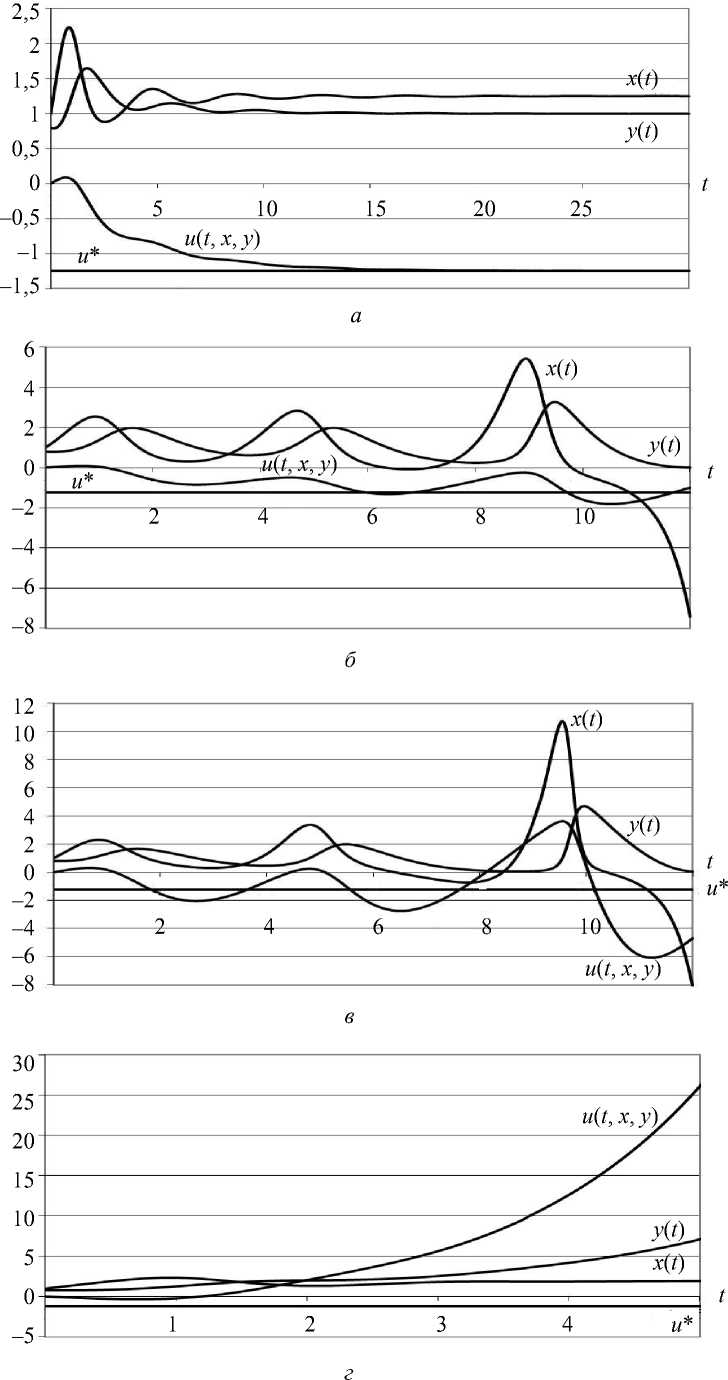
Рис. Результаты управления: а – вариант 1; б – вариант 2; в – вариант 3; г – вариант 4

1) K _П = 2, K И = 0,8, K _Д = 2, K _Д * = 1,25, K * = 1,95, X , «- 0,255, X ₂,₃ «- 0,173 ± i - 1,576;

2) K _П = 2, K И = 0,8, K _Д = 1, K Д * = 1,25, K * =- 0,65, X 1 «- 0,237,X ₂,₃ « 0,218 ± i - 1,730;

• 3)    K _П = 2, K И = 3, K _Д = 2, K Д * = 1,25, K * = 1,95, X 1 «- 0,852, X ₂,₃ « 0,126 ± i - 1,673;

• 4)    K _П = 2, K И =- 3, K _Д = 1, K Д * = 1,25, K * =- 0,65, X 1,₂ «- 0,293 ± i - 1,724, X ₃ « 0,785.

В варианте 1 выполняются оба условия (16)–(17) и наблюдается устойчивый выход на стационарные решения. В варианте 2 нарушаются оба условия (16)–(17) и видно, что в системе нарастают колебания, в результате которых численность жертвы становится отрицательной. В варианте 3 нарушается только условие (17), здесь качественное поведение решения аналогично варианту 2. В варианте 4 нарушается только условие (16) и наблюдается монотонный рост численности «хищника» и функции управления. Таким образом, данные расчетов подтверждают полученные выше теоретические оценки.

Идентификация параметров

Полученные результаты можно использовать при идентификации параметров реальной системы типа «хищник–жертва», для которой имеется возможность проводить серию экспериментов. В случае отсутствия управления тип особой точки «центр» и размерное время, за которое система совершает полный цикл, определяется из соотношения

T c =

2π

α1α2

Поскольку эта величина достаточно просто определяется из экспериментальных данных, то мы получаем соотношение для параметров системы

α1α2

2n

T к c )

Кроме того, эксперимент дает возможность оценить снизу и сверху отношение α₁ / β₁ . При применении стабилизирующего управления, обеспечивающего значение У , = A , количество «жертвы» и интегральная составляющая ПИД-регулятора стремятся к значениям (8)

X« = — = —, * к в к в 1

Г

U. = A 1 * к

к

;)

k

г

A

к

о . )

в 1 )

Таким образом, для определения четырех параметров системы (1) α₁, α₂, β₁, k мы имеем 3 соотношения (20)–(22). Если провести две серии экспериментов со стабилизацией численности «хищника» около значений A i ( i = 1, 2), получим

U ( i ) = *

a l f i - a 1 к к в J

A

к a1

J

i = 1,2.

Тогда из уравнений (23) имеем

A ₁ - A ₂

^k    _{U ∗} (1) _{- U ∗} (2) ^,

α1 = A -k⋅U(1), β1       1           ∗ и система уравнений (20), (21), (25) легко разрешается относительно неизвестных α1, α2, β1.

Таким образом, использование управления в виде ПИД-регулятора позволяет эффективно решать обратную задачу определения параметров классической системы «хищник–жертва».

Заключение

Таким образом, решена задача управления системой типа «хищник–жертва» с неизвестными заранее значениями параметров. При этом использован способ управления с обратной связью в виде ПИД-регулятора. Показано, что для рассматриваемой системы недостаточно ПИ-регулятора и только наличие Д-компоненты обеспечивает возможность устойчивого управления для любого соотношения параметров системы. В случае, если имеется возможность проводить натурные эксперименты, данный способ управления позволяет определить все параметры исследуемой системы, используя результаты двух серий испытаний с разным значением цели управления.