Управление сетью передачи данных на базе нейронных сетей

Постоянный рост количества пользователей Internet предъявляет новые требования к пропускной способности сетей связи и компьютерных сетей. Всемирная паутина привела к появлению различных видов трафика. Графическая информация, голосовые данные, а также видеоприложения предъявляют свои особые требования к таким сетям. Для удовлетворения всех запросов одного увеличения емкости сети недостаточно. Поскольку количество пользователей Internet и различных сетевых приложений увеличивается с каждым днем, сеть нуждается в средствах, которые обеспечивали бы поддержку как существующих, так и появляющихся новых приложений и служб.

Метод управления сетью передачи данных на основе искусственных нейронных сетей

Для управления современной сетью передачи данных необходимо применять эффективные методы маршрутизации, управления трафиком и контроля загруженности сети, которые основывались бы на данных, предоставляемых инструментом прогнозирования трафика на основе предыдущих значений.

Наиболее подходящим инструментом для прогнозирования являются ИНС [1]. Можно было бы использовать статистические методы, однако в настоящее время структура сетей очень быстро изменяется, и такие методы в некоторых случаях могут не справиться с данной задачей. В отличие от этих методов, использование ИНС позволяет не только выполнять заранее запрограммированную последовательность действий на заранее определенном наборе данных, но и анализировать вновь поступающую информацию, находить в ней закономерности, адаптироваться и проводить прогнозирование сети. Таким образом, ИНС непрерывно обучаются на основе предыдущих значений данных. Процесс обучения ИНС показан на рис. 1.

Рис.1. Процесс обучения ИНС

Рассмотрим формулировку и основные принципы организации вычислений при решении подобного рода задач. Пусть для некоторой группы узлов сети с известными расстояниями между ними требуется найти кратчайший маршрут. Обозначим узлы буквами А, В, С..., а расстояния между ними dAB, dAC,…dBC… Решением является упорядоченное множество из n узлов. Последовательность, в которой перебираются узлы, удобно представлять матрицей n×n, строки которой соот- ветствуют узлам, а столбцы номерам узлов в последовательности. Например, для пяти узлов А, В, С, D, Е последовательность обхода этих узлов может быть задана матрицей вида

А О   1   О   ОО

SOOO1O

С 1   0   0   00

£>0  0  0  01

£00100

Таким образом, узел С подключается первым, узел А – вторым и т.д. Длина маршрута равна d_CA + d_AE +…+ d_DC … В каждом столбце и в каждой строке этой матрицы может быть только одна единица, так как в каждый момент подключается только один узел и каждый узел подключается только один раз. Матрицу вида (1) можно воспринимать как состояние нейронной сети из N = n ² нейронов. Задача состоит в том, чтобы из ^2 , маршрутов выбрать один с наименьшей длиной. Состояние каждого нейрона описывается двумя индексами, которые соответствуют узлу и порядковому номеру его подключения в маршруте. Например, Y_xj = 1 показывает, что узел х был j -ым по порядку узлом маршрута.

Запишем функцию вычислительной энергии для сети, предназначенной для решения задачи маршрутизации, в которой состояние с наименьшей энергией соответствует самому короткому маршруту. В общем виде такая функция для рассматриваемой сети имеет следующий вид [1]

E—X-l.y.»,YiYl-y.l,Yl+lLT1Y„

I j J (2)

где Е – искусственная энергия сети, w_ij – вес от выхода нейрона i к входу нейрона j , Y_j – выход нейрона j , I_j – внешний вход нейрона j , Т_j – порог нейрона j .

Изменение энергии, вызванное изменением состояния j -го нейрона, можно вычислить следующим образом:

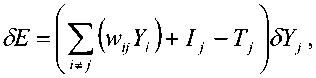
где 5Е – изменение выхода j -го нейрона.

Каждому состоянию системы соответствует конкретная величина вычислительной энергии. Устойчивое состояние имеет меньшую энергию, чем неустойчивое. Эволюция системы во времени

– это движение в пространстве состояний в поисках минимума энергии и остановка в этой точке.

Для рассматриваемой системы функция энергии должна удовлетворять следующим требованиям [2]: во-первых, она должна поддерживать устойчивые состояния в форме матрицы (1); во-вторых, из всех возможных решений функция энергии должна поддерживать те решения, которые соответствуют коротким маршрутам. Этим требованиям удовлетворяет функция энергии вида [1-2]:

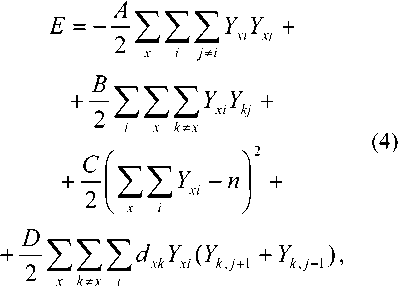
при этом Y_xj = 0; 1.

Первые три члена выражения (4) поддерживают первое требование, четвертый член – второе; А, В, С, D – положительные множители. Первый член равен нулю, если каждая строка х содержит не больше одной единицы. Второй член равен нулю, если каждый столбец содержит не более одной единицы. Третий член равен нулю, если в матрице вида (1) n единиц. Таким образом, без учета четвертого члена функция энергии имеет минимумы ( Е = 0) во всех состояниях, представленных матрицей с одной единицей в каждом столбце и каждой строке. Все другие состояния имеют более высокую энергию. Короткие маршруты поддерживает четвертый член. В нем индексы i берутся по mod n , для того чтобы показать, что i -ый узел соседствует в маршруте с ( n – 1)-ым и первым, то есть Y_k,n+j = Y_kj . Четвертый член численно равен длине маршрута.

Раскрывая скобки в (4) и приравнивая коэффициенты при квадратичных и линейных членах в полученном выражении и общей формуле энергии [1], определяем матрицу связей и внешние взаимодействия:

w^AS^-SyVBS^-S^-

-C-Ddxk(5,,w +Shi_^ , где 5y = 1, если i = j, в противном случае 5y = 0. Кроме того, каждый нейрон имеет смещающий вес Ixi = Сп.

Первый член в (5) задает связи нейронов в каждой строке, второй – внутри каждого столбца, третий и четвертый – глобальные связи. И в (4) и в (5) три первых члена отвечают за общие ограничения для любой задачи маршрутизации и приводят сеть к финальному состоянию в виде (1). Четвертый член управляет тем, какое из ^П/2п возможных различных финальных состояний соответствует самому короткому маршруту.

Выбор маршрутов, максимизирующих степень узла в сети, позволяет спланировать работу так, чтобы время ее выполнения было минимальным. Степень узла для этого случая, определяется как сумма всех потоков, поступающих в узел и исходящих от узла. Например, линия, которая должна активироваться, три раза добавляет поток из трех единиц к обоим узлам, которые она соединяет. При этом критерий качества работы, выбираемый для задачи маршрутизации, должен отражать цели, связанные с соответствующей задачей составления плана работы линий связи. Показатель качества работы должен согласовываться со структурой соответствующей ИНС.

Выходные напряжения нейронов, которые и определяют их состояния, такой ИНС приближаются к двоичным значениям по мере перехода сети к состоянию устойчивого равновесия с минимальной «энергией». Соединения между нейронами i и j описываются весом T_ij , который положителен, если соединение возбуждающее, и отрицателен, если соединение тормозящее.

Иногда ИНС не может провести распознавание образов (образцов) и выдает на выходе несуществующий образ. Это связано с проблемой ограниченности возможностей искусственной нейронной сети. Так, для ИНС Хопфилда число запоминаемых образов m не должно превышать значения равного 0,15 n . Кроме того, если два образа А и Б сильно похожи, они могут вызывать у сети перекрестные ассоциации, то есть предъявление на входы сети вектора А приведет к появлению на ее выходах вектора Б и наоборот. Еще одним недостатком сетей Хопфилда является их тенденция стабилизироваться в локальном, а не в глобальном минимуме.

В тех случаях, когда не требуется, чтобы ИНС в явном виде выдавала образ (образец), т.е. достаточно получить номер образца, задача может быть успешно решена с помощью ИНС Хэмминга (см. рис. 2). Модели на основе ИНС Хэмминга, по сравнению с ИНС Хопфилда, имеют меньшие затраты на память и объем вычислений. ИНС Хэмминга состоит из двух слоев: первый и второй слои имеют m нейронов, где m – число образ- цов. Нейроны первого слоя имеют по n синапсов, соединенных с входами сети. Нейроны второго слоя связаны между собой отрицательными обратными синаптическими связями. Роль первого слоя условна, воспользовавшись один раз на 1-ом шаге значениями его весовых коэффициентов, сеть больше не обращается к нему. Поэтому первый слой может быть исключен из сети и заменен на матрицу весовых коэффициентов.

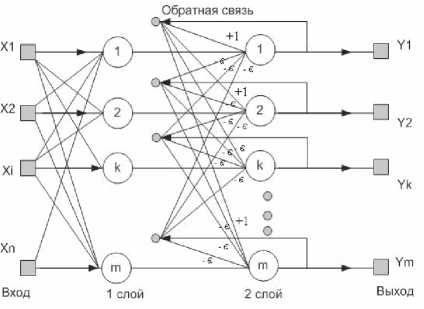
Рис. 2. Структурная схема ИНС Хэмминга

Идея работы ИНС Хэмминга – определение расстояния Хэмминга от тестируемого образца до всех образцов. Расстоянием Хэмминга называется число отличающихся битов в двух бинарных векторах. Сеть должна выбрать образец с минимальным расстоянием Хэмминга до неизвестного входного сигнала, в результате активизируется только один выход сети, соответствующий данному образцу.

Наиболее широко применяемый протокол в Internet сетях это протокол TCP/IP. Для ускорения и оптимизации процесса передачи больших объемов данных протокол TCP определяет метод управления потоком, называемый методом скользящего окна, который позволяет отправителю посылать очередной сегмент, не дожидаясь подтверждения о получении в пункте назначения предшествующего сегмента [3].

Если заранее получать данные о переполнении буфера оборудования или возрастающих задержках в сети, то можно управлять сетью для предотвращения потери данных и увеличения сохранности передаваемой информации. Решение этой задачи производится ИНС Хэмминга, на вход которой подаются данные об объеме буфера или задержках в сети. Данная ИНС позволяет прогнозировать будущее поведение трафика сети на основе известных данных, собранных заранее.

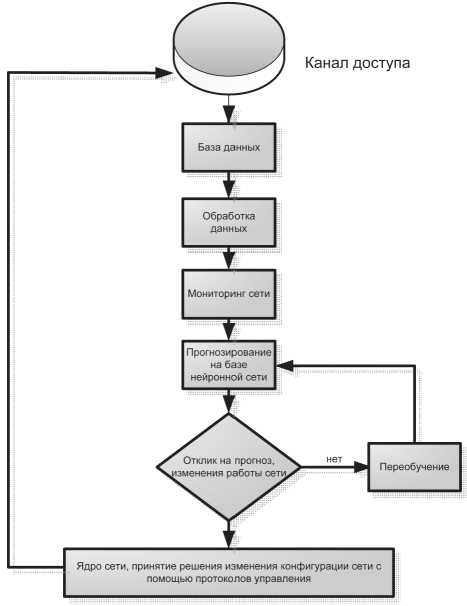
Рис. 3. Алгоритм управления сетью передачи данных на базе ИНС

Ниже представлена блок-схема алгоритма, реализующего прогноз и принятие решения для управления сетью передачи данных, который иллюстрирует рис. 3. В качестве входных данных для процесса прогнозирования нейронной сети используются заранее собранные данные о трафике сети в блоке базы данных. Поступивший трафик N анализируется на наличие необходимых элементов: широкополосный трафик, избыточность, задержка сети, полоса пропускания, надежность и загруженность сети. На основе выбранных данных происходит прогнозирование повторного появления выбранного объекта исследования ( N + 1). Шаг прогнозирования можно увеличить, но при этом достоверность прогноза уменьшается.

На основе спрогнозированных данных происходит воздействие на сеть: под воздействием понимается активация сетевых команд для предотвращения появления спрогнозированного объекта (управляющее воздействие на пропускную способность канала, очистка буферов активных сетевых элементов, активации фильтров и т.д.).

Заключение

Вопросы прогнозирования и управления трафиком современных сетей передачи данных очень важны и требуют самого пристального внимания. Наиболее хорошо обучаемыми для целей прогнозирования в настоящее время являются искусственные нейронные сети. Предложенный метод управления сетью передачи данных на базе обучаемых ИНС обеспечивает прогнозирование трафика, более стабильную работу сети передачи данных с сохранением самих данных, и как следствие сокращение времени простоя сети в случаях обнаружения нежелательного трафика.