Управление в бинарных моделях с разладкой

Процессы со сменой режимов находятся в сфере постоянных интересов исследователей. Специальный класс этих процессов называют процессами с разладкой. В этой связи, следует отметить работы Ширяева и его учеников [1–5], в которых изучается задача быстрого обнаружения разладки. В [6] процессы с разладкой применялись как средство аппроксимации решения стохастического дифференциального уравнения. В [6] разладки совпадали с моментами достижений случайными процессами определенных уровней, то есть являлись моментами остановки.

Число работ, посвященных обнаружению разладки, с каждым годом растет. Поиск по базе данных arxiv.org показывает больше ста работ за 2021 год, так или иначе связанных с проблемой обнаружения разладки в случайном процессе. Несомненно, существует потребность в алгоритмах решения задач оптимального управления для процессов с разладкой. Работ, связанных с оптимальным управлением процессами с разладкой, по-видимому, значительно меньше. В этой же базе данных не удалось обнаружить ни одной.

В работе [7] рассматривались задачи управления в моделях со сменой режимов в случайные моменты времени, которые были моментами остановки.

В статье рассматривается бинарная аппроксимация модели Блэка – Шоулза с разладкой, поскольку, на наш взгляд, бинарная модель с разладкой – единственная модель, которая предоставляет возможность получения вычислительного результата при вычислении оптимального управления для этой модели.

В большом количестве работ изучают бинарную аппроксимацию диффузионных процессов. В основном эти работы посвящены сходимости биномиальной цены финансового обязательства к цене Блэка – Шоулса. Первое доказательство сходимости биномиальной цены опциона к цене Блэка–Шоулза было дано в работе Кокса, Росса и Рубинштейна [8]. Более общее доказательство сходимости было приведено в работе Hsia [9]. Первая оценка разницы между биномиальной ценой и ценой Блэка – Шоулса была дана в работе Heston and Zhou [10]. Эта оценка была порядка 1Д/П- Для финансовых обязательств опционов европейского типа эта оценка имеет порядок 1/n. Эту оценку можно найти в работах [11–13]. Заметим лишь, что для специальных случаев были получены оценки более высоких порядков, см., например, работы [14, 15].

Для получения бинарной аппроксимации диффузии мы используем результаты работы [16]. Остановимся на этой работе. В работе рассматривается стохастическое дифференциальное уравнение: dYt = ^(Yt,t) dt + a(Yt,t) dWt, с начальным значением Yo. В уравнении Wt - стандартный винеровский процесс. Предлагаемая бинарная аппроксимация Y является процессом с кусочно-постоянными траекториями, скачки траекторий происходят в фиксированные моменты времени, которые находятся на расстоянии h друг от друга. Размер скачков вверх или скачков вниз, а также вероятности вверх или вниз определяются тремя функ- циями: U (y, t, h) = ^

h^⁽y^,t),D(y^,t,h) = ^— VMy,^ и q(y,t,h). Таким образом,

(Ay = C/Yt i)^ = q(Y (h - ₁) ₁ , (i —

Y th = Y ₀ + 52 AY ih l ^ ih ^ t } . Условная вероятность P i=1

-

^{1)h h )} I {c=u(y^h, ,(i - 1)h,h) } + (1

q(Y(h-1)h, (i — 1)h,h))I{c=D(Y(t1)h,(i-1)h,h)}. Вероят- ность q выбирается из условия: E (AYih/Y^-^h) = ^(Y(i_1)h, (i — 1)h)h. Отсюда q(y, t, h) = 2 + ^(y^y, с естественным ограничением на параметры в виде неравенства: Му^1Vh < ^(y,t).

В работе [16] гарантируется слабая сходимость кусочно-постоянных случайных траекторий к решению стохастического дифференциального уравнения при выполнении следующих условий:

t

• 1)    уравнение имеет единственное сильное решение Y _t = Y ₀ + J ^(Y s , s) ds +

t

J a(Y s ,t) dW s ;

• 2)    функции ^(y,t), a(y,t) - непрерывные функции, функция a(y,t) - неотрицательная ограниченная функция.

Из слабой сходимости кусочно-постоянных траекторий следует сходимость средних от функционалов на кусочно-постоянных траекториях, и скорость сходимости, как отмечалось выше, имеет порядок 1 /n .

В качестве примера управления случайным процессом с разладкой в работе рассматривается динамическая задача управления портфелем. Динамическая задача управления портфелем инвестиций относится к задачам оптимального управления случайными процессами.

Несмотря на очевидную значимость динамической задачи, основные результаты получены для одношаговой модели. Для одношаговой модели задача впервые рассмотрена Марковицем [17]. С момента ее публикации на эту работу насчитывается более 25 000 ссылок, однако, качественно отличающиеся от диверсификации по Марковицу результаты были получены в конце 90-х. В связи с этим отметим работу Рокфеллера и Урясева [18]. В нашей работе использованы критерий из работы Марковица и критерий из работы Рокафеллера и Урясева, а также несимметричный критерий качества портфеля, заимствованный из машинного обучения [19].

Работы по динамическому управлению портфелем в основном связаны с машинным обучением, применяемом для построения стационарного портфеля. Поскольку машинное обучение не связано с темой данной работы, приведем лишь одну из монографий, посвященных машинному обучению в связи с оптимальными инвестициями [20]. Данная монография наиболее полно излагает методы машинного обучения, которые используются для вычисления оптимального портфеля.

Структура работы такова. Второй раздел посвящен разладке в бинарной последовательности. Основной результат заключается в сопоставлении разладки с кластеризацией вершин дерева на два класса. К первому классу относятся вершины, в которых происходит разладка. Сначала вершины бинарного дерева разделяются на два класса моментом остановки, оценивающем разладку, затем излагается нечеткая кластеризация. Для четкой кластеризации, бинарная последовательность рассматривается как случайное блуждание по вершинам дерева, и оценкой разладки является минимальный момент времени, в который случайное блуждание оказывается в вершине первого класса при четкой кластеризации. При нечеткой кластеризации используется схема Монте-Карло.

В третьем разделе рассматривается популярная в финансовой математике модель Кокса – Росса – Рубинштейна с добавлением разладки. В этом же разделе решается одна из задач оптимального управления, которая относится к динамическому управлению портфелем инвестиций.

Четвертый раздел посвящен вычислительным примерам, в задачу которых входит в основном иллюстрация предложенных методов.

1.    Оценка разладки

Стохастическая модель разладки. Рассмотрим бинарный случайный процесс X t со значениями X t Е { 0,1 } и дискретным временем t Е { 1,...,n,... } на естественном стохастическом базисе - ( Q, (F _n ) _n> 1 ,F, P ) . В базисе пространство элементарных случайных событий Q - множество бинарных последовательностей ш = (^ 1 ,..., ш _п ,...), элементы фильтрации а-подалгебры F n = а(Х 1 , ..., X _n ), а-алгебра F = U _n> 1 F _n , P - вероятность. Рассмотрим случайную величину 6 Е { 1, ... ,n,... } , которую будем называть разладкой. Для любой последовательности ω определена условная элементарная вероятность р (ш/6 = п), и определено распределение вероятностей для случайной величины 6 — р(п). Элементарная вероятность вычисляется по формуле полной вероятности р(ш) = ^ р (ш/6 = п) р(п).

n > 1

Будем считать, что определены два типа элементарных вероятностей р ₀ (ш) и р ^ (ш ). В этих элементарных вероятностях содержатся два крайних случая: разладка наступила с самого начала и разладка не наступила.

Для условной вероятности будем использовать следующую формулу:

Р (ш/6 = п) = Р ^ (Ш 1 , . . . , Ш п - 1 )р о (Ш п , Ш п+1 , ...,Ш т ,... ),

Р (ш/6 = 1) = Р о (Ш 1 ,Ш 2 , . . . ,Ш т , . . . ).                                       (1)

То есть последовательность ω составляется из двух независимых подпоследовательностей. Кроме этого, р ^ (ш х ,..., Ш п - 1 ) = Пи Р ^ (ш i ), Р о (ш х ,..., Ш п - 1 ) = П i > n Р ₀ (ш _i ). Для каждого фактора в этих формулах справедливо выражение:

Р о (ш i ) = q ^ (1 — q o ) ' ■ , р ^ (ш i ) = q . (1 — q . ) ^{1 -} ^ .                   (2)

Информационное дерево и моменты остановки. В связи с бинарной последовательностью рассмотрим бинарное дерево с набором вершин [(A j ) 2₌₀ ¹ ]N_{= 0} в котором A ^j ^ { A 2-+ 1 , A 2++ ¹ } . Нетрудно установить изоморфизм между отрезками бинарной последовательности ω и вершинами дерева A _i ^j . Этот изоморфизм задается стандартным образом: отрезок бинарной последовательности ω изоморфен вершине i

A j тогда и только тогда, когда j = ^2 2 i - k ш _к .

k=1

Рассмотрим произвольный момент остановки τ . Момент остановки разделяет вершины дерева на два класса в соответствии с правилом: вершина A _i ^j относится к первому классу (H i ) вершин, если т(A j ) = i; если A j относится к первому классу, то вершины A j 1 и A j¹ также относятся к первому классу, естественно т(А^ 1 ) = т (A j ¹ ) = i. Остальные вершины дерева относятся ко второму классу (H ₂ ). Теперь последовательность ω можно рассматривать как случайное блуждание по бинарному дереву, если блуждание в некоторый момент времени оказывается в вершине первого класса, то оставшаяся часть блуждания будет происходить по вершинам этого класса.

Задача оценки разладки. Задача обнаружения разладки заключается в вычислении момента остановки τ ∗ , расположенного как можно ближе к случайной величине θ . В упомянутых ранее работах задача обнаружения разладки рассматривается как задача оптимальной остановки марковского процесса [14]. Линейный критерий в задаче об оптимальной остановке имеет вид: P(9 > т ) + аЕ(т — 9) ⁺ . Первое слагаемое -вероятность «ложной тревоги», второе – среднее запаздывание. Стандартным образом показывается [8], что задача об оптимальной остановке для дискретного времени и конечным горизонтом с приведенным критерием сводится к следующей задаче оптимальной остановки:

т — 1

V =

min

0 < т < Т

E[1 ^— у_т + ^а ^^ y i \.

i=1

В (3) y _n = P (9 ^ n/F n ) — последовательность апостериорных вероятностей. По формуле Байеса:

n

Е p (X 1 ,X ₂ ,...,X n /9 = j ) P (9 = j )

ϕ n

j=1 ________________________________________

p(X 1 ,...,X n )

Одновременно с этой последовательностью рассмотрим последовательность отношений правдоподобия:

E p (X 1 ,...,X n /9 = j) P (9 = j )

У п   = j =0 _____________________________

1 — У п” p . (X 1 ,...,X n )P (9 > n)

Задача (3) выражается в терминах этой последовательности следующим образом:

V = min E [ + a   ——— ] .

¹< т < T [ 1 + ф т     ^=1 ^ i + 1 j

Последовательность отношений правдоподобия является достаточной статистикой для оценки разладки и может быть использована непосредственно для оценки разладки, например, следующим образом:

т = inf { n: ф _п ^ a } .

Порог a может быть выбран, исходя из разных соображений. Например, исходя из ограничения: E (т = _TO) ^ T , где T - параметр, принимающий большое значение. Смысл ограничения заключается в следующем. Среднее время неправильного обнаружения разладки (ложной тревоги) должно быть большим.

С помощью последовательности отношений правдоподобия можно реализовать нечеткую кластеризацию вершин дерева. Будем считать, что принадлежность вершины Ain к первому классу является случайным событием, вероятность которого i Фп(An)

P^{(А п е Я 1 )}"1+ * „ (А п ) •

При нечеткой кластеризации может быть использована схема Монте-Карло. В этой схеме одновременно с вычислением отношений правдоподобия генерируется последовательность независимых равномерно распределенных на интервале [0,1] случайных величин ν n , и оценка разладки вычисляется следующим образом:

т = inf

{ n :

ν n

<

ψ n

• ¹    + ^ф п

.

Последовательность отношений правдоподобия. Для кластеризации вершин дерева необходимо вычислить значение последовательности отношений правдоподобия ψ n в каждой вершине дерева. При независимости и одинаковой распределенности нужные вероятности имеют следующий вид:

к —1

p _ (X 1 ,..., X k - 1 ) = (1 - q . ) ^k-1 (           i ^¹ i

• V¹ - q^z

,

n

X i

P o (X k , X k+1 , ...,X n ) = (1 - q o ) ^n-k-1 1 -°^ J i = k

.

Отсюда

n n              Xi

,... ,X n ) = P _{( 6} >  _{n )} £U'^R-1 P (6 = k),

L = J¹' " , R = q ⁰ '',- ^ ) . Для вывода рекуррентного уравнения рассмотрим

ф п+1 (X 1 ’ . . . ’ X n+1 ) =

P (6 > n) Г LR X n +1 у L-+«RtkXip<6 = J = P(6>n + 1) PP (6>n) k=1       R     (   k)] P         [ LR^ . ( фГ (X,..., .у + P          ) 1 . p(6 > n +1) [        \                    p (6 > n) /_

Данное рекуррентное уравнение можно связать с вершинами дерева:

ф п+1 ( А 2 + )

P (6>n)            iX ,P (6 = n +1)M p(6>n + 1) [LR Vn (A n ) 1    P(6>n)     ’        (6)

2i         ^{P 6} ' UlAq ^{P ( 6} = n + 1)

^{Ф п+1 (А п} +1 )      p(6>n +1) [LT n ^{(A n )+} P (6>n) J]’

ф 1 (А 1 )

= LrP^ , Ф1 (A 0 ) = lP(^=4. P (6 > 1)’         1J     P (6 > 1)

Уравнение (6) позволяет вычислить отношение правдоподобия для всех вершин де-

рева.

Рассмотрим пример с геометрическим законом распределения разладки P (6 =

j ) = (1 — A)A j 1 , j = 1,.... Необходимые для расчетов отношения:

P (6 = n + 1) P (6 > n)

P (6 > n) p(6 > n + 1)

1 λ,

= 1 — А, являются постоянными, что позволяет записать равенство (5)

следующим образом:

ф п (X 1 ,...,X n ) = (1 - А)

/L\ ^{n +1}    /АА k _nE X i

Vа) и Ыл“

.

2.    Оценка разладки

Оптимальный портфель для бинарной модели. В работе [22] исследована задача:

min E ^(Y(T),()),

β Y/X ^, y 0

при ограничениях

Y ^{(t) —} y o +

t

I e Y/x (s) dX s , t E [0,T], 0

X (t) — X o +

t

I a x (s) ds +

t

I в х (s) dW s , 0

yo < a, и предложен метод ее решения. Функция Ф(х, у) - выпуклая по первому аргументу функция при любом значении второго аргумента. Естественным дискретным, бинарным аналогом данной задачи является задача следующего вида:

^min E⁽Ф^(Y N ,()) β Y/X ^,y 0

при ограничениях:

n

Yn — Уо + ^ eY/U (i)AUi,  n Е {!,..., N}, i=1

AU n — ^(U n - 1 )a n

/ bn И an      ,

X n E { 0,1 } ,

У о <  a.

Уравнение (9) рассматривается на естественном стохастическом базисе: (Q, (F)n,F,P\ F0 — ^{0, Q}, Fn — ^{X1,... ,Xn}. Для этого базиса случайные величины an, bn, eY/x(n) — предсказуемы (an,bn,ву/х(n) E Fn-1). Условная вероятность P(Xn — 1|Fn-1) — pn, pn - предсказуемая случайная величина. Предположим, что существует единственная мартингальная мера P*: E*(AUn|Fn-1) — 0, и задача min E(Ф(п,£)) при условии E*п ^ а имеет решение - п*, то решение задачи (7) имеет η решение, которое получается следующим образом:

• 1)    вычисляется мартингал U n — E * (n * | F n );

• 2)    вычисляется разложение мартингала Y по мартингалу U : Y _n — у о + n

У^ e Y/u (i)AU i . Существование разложения следует из единственности мартин- i =1

гальной меры. Подробнее см. [21].

Таким образом, для решения задачи мартингальным методом требуется суще- ствование и единственность мартингальной меры. Для вычисления мартингальной меры необходимым и достаточным условием является равенство: E*(AUn|Fn-1) — 0

- a n _. b _n - a _n

или b n р П + a n (1 — р П ) — 0. Решением этого уравнения является величина р П —

Поскольку р* - вероятность, то должно выполняться неравенство: 0 < -t—an- < 1. Это n                                                                            bn -an двойное неравенство будет выполняться, если an < 0 < bn. Таким образом, единствен- ная мартингальная мера существует, если выполняется данное двойное неравенство для параметров модели.

Модель с разладкой. Рассмотрим следующую модель:

AU n = _V(U n - 1 )a n (—A , X n g{ 0, 1 } , P(X n = 1/n<9) = q _ , a _n

P (X n = 1/n >  9 q o .

Бинарной последовательности X соответствует информационное дерево. Применяя методы, изложенные в предыдущем разделе, вычисляем момент остановки, оценивающий разладку, который разделяет вершины дерева на два класса – H ₁ , H ₂ . В соответствии с классификацией вершин бинарного дерева определяют-

ся

параметры модели: a _n

₂ n -1 _{- 1}

E а(АП-1 )I(An-1), a«-1) = i=0

^ 1 , A n - 1 ^G H 2

М 2 , A n - 1 ^G H 1 ,

b n

² n -1 ^-1 v A i G H

E ^An—JI(An-1), b(An—1) = i ,,’             • Исходная мера в данной i=o                                   I V2, An-1 G H1

модели вычисляется с помощью рекуррентных уравнений:

A 2»+^     / q 0 ^P (A nn - 1 ),

^{P (}A ⁿ ) = I q ^ P(A n - i ),

i ^A n - 1

i ^A n - 1

^G H 1 A2^ = / ^{(1 — q} o ^)P(A n - 1 ),  A n - 1

G H 2 ’ P⁽A ⁿ )   1 (1 — q . )P (A n - 1 ), A n - 1

G

G

H 1

H 2 ^,

Мартингальная мера в

P (A 0 ) = 1.

данной модели вычисляется следующим образом:

P * (АЩ ⁺1 )= q(A n - i )P * (A n - i ),

P * (A 2i ) = (1 - q(A n - i ))P * (A n - i ),

q(A n — 1 ) =

^— М 1

^V 1 ^— М 1 ’

- М 2

^v 2 ^— М 2 ’

^{A i} n - 1 ^{G H} 2

A ⁱ _{n- 1} G H 1

p * (A 0 ) = 1.

Для существования и единственности мартингальной меры достаточным условием является выполнение неравенств: м ₁ < 0 < v ₁ , м 2 < 0 < v ₂ .

Оптимальное управление портфелем. Далее мы будем рассматривать задачу оптимального управления динамическим портфелем для уравнения Кокса–Росса– Рубинштейна (КРР) с разладкой. Задача заключается в выборе оптимальной стратегии инвестиций γ в рисковый актив, стоимость которого S подчиняется КРР уравнению:

AS n = S n - 1 a n (b n ) a n

,

X n G{ 0,1 } , P(X n = 1/n<0) = q ^ ,

P(X n = 1/n >  9) = q o •

Уравнение (10) является частным случаем уравнения (8). Эффект от динамического портфеля п = (Y,e) — выражается в капитале Y. Капитал Yn = YnSn + enBn, в этом равенстве Bn – стоимость безрискового актива, например, стоимость банковского счета. Безрисковость второго актива, входящего в портфель, означает, что стоимости Bn являются константами. Не нарушая общности, можно считать, что Bn = 1. Портфель называется самофинансируемым если: AYn = YnASn. Качество портфеля определяется доходностью портфеля в некий финальный момент времени N: RN = YN. Будем считать, опять же не нарушая общности, что Yo = 1, и известна цель - целевая доходность, выраженная случайной величиной ξ , которая предполагается неотрицательной и ограниченной. При этом штраф взымается, если капитал не совпадает с целью. Средний квадратический штраф, штраф по Марковицу [17] приводит к задаче min E(£ — Yn)2, AYn = YnASn,E*Yn = 1, Yn > 0            (11)

γ

AS n удовлетворяет уравнению (9). Последнее неравенство означает, что рассматриваются допустимые портфели, капитал, которых неотрицателен.

Решение задачи (11) начнем с предложения, утверждающего, что все участвующие в задаче (11) случайные величины интегрируемы с квадратом.

Действительно, во-первых, для конечного пространства элементарных случайных событий свойство интегрируемости с квадратом эквивалентно свойству ограниченности, при условии, что все атомы нагружены, во-вторых, цель ξ и стоимости рискового актива S n – ограниченные случайные величины по естественным причинам. Отсюда непосредственно следует ограниченность случайных величин Y _n .

Следуя схеме, изложенной ранее, для решения задачи (11) следует решить задачу:

min E (£ — n) ² , E * п = 1, П ^ 0.                       (12)

η

Без последнего ограничения решение задачи (12) можно найти с помощью функции Лагранжа. Решение задачи будет иметь вид:

*    .   1 — E * (

^П = ^⁺   E * Z z.

В этой формуле значение случайной величины z в вершине A N : Z(A N ) = P_p(AN. ) .

P (A N )

Для того, чтобы портфель был допустимым, должно выполняться неравенство: £ + 1 — E * £

_ z >  0.

E ^* Z

Далее применяется схема вычисления портфеля, приведенная выше.

Приведем пример, использования среднего квадратического портфеля. Допустим, мы хотим выяснить, возможно ли получить доходность выше доходности рискового актива, используя средний квадратический портфель или портфель оптимальный по Марковицу. Ответ заключается в следующем. Это можно сделать тогда и только тогда, когда So > E*Sn • Действительно, в качестве цели определим доходность £ = a SN, a > 1 и подставим ее в формулу для доходности оптимального портфе- а т? * о

_S E S _N

⁰ z . Необходимым и достаточным

E * z

1 —

ля, в результате получим п* = a —N- + So условием выполнения неравенства п* > £ является неравенство a < ES-• Отсюда непосредственно следует приведенное утверждение. N

Недостатком среднего квадратического штрафа является его симметричности. В качестве несимметричного штрафа можно предложить следующий штраф: f (x, y) = max { y — x, 0 } , который применяется машинном обучении [19]. С таким штрафом вспомогательная задача об оптимальном портфеле будет иметь вид:

min E max { £ +1 — п, 0 } , E * п = 1, П ^ 0. ^η

Является справедливым неравенство I { _n< ^ } С max { £ + 1 — п, 0 } , поэтому P(п N £) С E max { £ + 1 — п, 0 } .

Анализ задачи. В задаче (13) целевая функция является выпуклой, единственное ограничение линейное, поэтому можно использовать сильную двойственность [23]. Двойственная задача выглядит следующим образом max min(E max{£ + 1 — n, 0} + ц(ЕП— — ^ Ln>0 x

Легко проверяется следующее утверждение.

Утверждение 1. Оптимальное значение µ больше либо равно нуля.

Пусть F(м) = min(E max{^ + 1 — n, 0} + ^(E*n — 1)). Упорядочим по возрастанию последовательность отношений Z(i) = P-^ANN)-, и рассмотрим разбиение положительной P (AN)

полуоси R ₊ точками Z (i) - Непосредственным вычислением доказывается справедливость следующего утверждения.

Утверждение 2. Функция F(м) - вогнутая кусочно-линейная функция, определя-j                       2NNi емая равенством F(м) = J2p(i)«i + 1) + Ml S Pu)(Ci + 1) - 1 ), Z(j) < M < Z(j+1). i=0                   4=j+1                  '

В этом равенстве p (i) = P (A ^) ) , P (i) = P * (А^) .

2 N - 1

Пусть k * = min { j: ^ pE(C (i) + 1) ^ 1 } . Используя утверждение (2), получим i=j+1

решение задачи (13). Это решение имеет следующий вид:

<

П (*) = ^<

0,

2 N -1

1 - E p ( _г ) (£_w+1) i = k * + 1

p ( k ‘)

^ (i) + 1,

ik .

При этом оптимальное значение м * = Z (k * ) .

После того как найдено η , вычисляется оптимальный портфель.

Оптимальный портфель для модели Блэка – Шоулса с разладкой. В модели Блэка – Шоулса с разладкой эволюция стоимости рискового актива описывается с помощью уравнения:

dS t = S t (( m i I(t <  9) + m ₂ I(t ^ 9) ) dt + adW t ) ,

с заданным начальным значением S ₀ . В (14) W _t - винеровский процесс.

Для приближения модели (14) бинарной моделью, моделью КРР, используем результаты уже упомянутой работы [16]. Интервал [0, T] разбивается на N частей с шагом h = T/N . Бинарное приближение имеет вид:

N

S h = S o +Е^Д5 «К I { ih« } ,  ^ ^si h = S h - 1)h aVh(— 1) ^X - ⁺¹ .           (15)

i=1

c условными вероятностями q ^ = P (X i = 1/i <  9) = 2 + ^ ¹ ₂ ^^h , q ₀ = P (X i = 1/i ^ 9) = 2 + ^ 7 >^h . Все остальные вычисления производятся также, как и в предыдущем разделе.

Редукция NP -полной задачи к P -полной задаче. Рассматриваемые задачи являются N P -полными, однако формулы (15), с помощью которых вычисляется стоимость рискового актива, позволяют редуцировать N P -полную задачу к P -полной задаче. Для этого рассмотрим случайное блуждание: Z o = 0, Z n = Z n - i + X " , которое образует марковскую цепь. Рассмотрим дерево с вершинами { А " } "=₀ , n = 1, 2,..., N, и дугами А П ^ А "+₁ , А " ^ А "+¹ ₁ , которое соответствует этому случайному блужданию. Стоимость актива в точках разбиения выражается через случайное блуждание следующим образом: S hh = S h (1 + aVh) ^{Z n} (1 — a\/hj" ^zn , и поэтому связана с вершинами дерева. Для управления процессами с разладкой требуется классификация вершин дерева с использованием двух классов. Для данного дерева мы используем нечеткую классификацию. Мы будем рассматривать принадлежность вершины классу как случайное событие, которое наступает с апостериорной вероятностью P(A " G H ₁ ) = р _П , ₍ . Далее мы будем считать, что случайная величина ξ в целевом функционале задачи (11) будет функцией от стоимости рискового актива £ (S N ). Для решения задачи (11) нам потребуется вычислить вероятности, связанные с вершинами последнего слоя – P(A^k N ). Аналогично тому, как это было сделано в предыдущем разделе, вычисления производятся с помощью рекуррентных формул:

P (А 0 ) = 1, P (А " )= P (A " - i ) ( (1 — q o )P n - i,o + (1 — q - )(1 — Р п - 1,0 ) ) ,    (16)

^{P (А} П ) = ^P(А П - 1 ) ( ^q o ^p n - 1,n + ^q ^ ^{(1 — р} п - 1,п ) ) ,

^{P (А} П ) = ^{P (А} П - 1 ) ( ^{(1 — q} 0 ^)p n - 1,i + ^{(1 — q} ^ ^{)(1 — p} " - 1,i ⁾ ) +

+ ^{P (А} _П- 1 ) ( ^q 0 ^p n — 1,( + ^q ^ ^{(1 p} n — 1,i ⁾ ) , i = ⁰, i = ⁿ-

Мартингальная мера вычисляется аналогично тому, как это было сделано в предыдущем разделе. Для мартингальной меры вероятности, связанные с вершинами последнего слоя P * (A N ) = C N (2) . Дальнейшие расчеты приведены в предыдущем разделе. Отметим, что порядок числа необходимых вычислений сократился с 2 N ⁺¹ до N ² .

Вероятности p _n,i . Для расчетов по формулам (16) требуются вероятности p _n,i .

n

Рассмотрим Z " (i) = 52 P (Z " = i/9 = j )P (9 = j ), i = 0,1,...,n; и рекуррентное j =1

уравнение, связывающее Z"(i) и Z"+1(i)- Сперва приведем формулу для Z"+1(0) = (1—q0) (Zn(0) + (1—q^)"P(9 = n+1)), затем для Zn+1(n+1) = q0(Z"(n)+qnP(9 = n+1)), и наконец Zn+1(i) = q0^Z"(i — 1) + Cn-1qi-1(1 — q^)"-i+1P(9 = n + 1)) + (1 — q0)(Z"(i) + Ciq^o (1 — q-)"-iP(9 = n + 1)), i = 1, 2,-.., n. Для начальных значений справедливы равенства: Z1(0) = P(X1 = 0/9 = 1) = 1 — q0, Z1(1) = P(X1 = 1/9 = 1) = q0. Ве p (e^n/Zn=i) p (o>n/Zn=i)

личины Z " (i) позволяют вычислить отношения правдоподобия ^ _П (i) =

Z n (i)P (9 < n) C n qi^ (1 - q ^ ) ^{n - i} P (9>n)

, а отношения правдоподобия, в свою очередь, позволяют вычис- лить вероятности рП^ = 1+"n(i(i). Последние равенства завершают необходимые для расчетов формулы.

3.    Вычислительные примеры

Обнаружение разладки. Рассматривается стохастическое дифференциальное уравнение с разладкой:

dYt = (m1I{t <9} + m2I{t > 9}) dt + adWt, в котором Wt – стандартный винеровский процесс, случайная величина θ распределена по показательному закону распределения с плотностью pg (x) = ^e-^t. Одновременно с этим уравнением рассматривается соответствующее дискретное уравнение:

AY i = ( m 1 I { i <9 } + m ₂ 1 { i >  9 }) h + aVhe i , в котором h – шаг разбиения оси времени, θ – случайная величина с геометрическим распределением вероятностей P(9 = j) = (1 — A)A j ^-1 , j ^ 1, E i - независимые стандартные нормальные случайные величины. Параметр A = e ^- ^ ^h . Последовательность Y i приближается бинарной последовательностью Y i следующим образом

Y i = Y - 1 + ( — aVh)^{1 +Xi} , в которой X i = {

1, Y i

0, Y

Y i - 1

Y i - 1

> 0

< 0 . При таком приближе-

нии условные вероятности q _∞

= P (X i = 1/i <  9) = 2

+    . , q o = p (X i = 1/i <

9) = 2 +

2σ

. Задача о разладке рассматривается на интервале [0,1] с начальным значением Yo = 0, параметр ^ выбирается из условия P(9 > 1) ^ —, то есть ^ = ln а.

Было проведено значительное число экспериментов с разными значениями параметров, результаты одного из них приведены ниже. Определим значения параметров. Пусть

— = 0,0005, m1 = 0,5, m2 = 1,5, a = 0,2, N = 100, h = 0,01, M = 1000, a = aVh = 0,02, д = In ^—^ « 7,6, A = exp(-^h) ~ 0,93, тогда

q ^ = 0,5 + ^h = 0,625.

2a по формуле:

q o = 0,5 + ^2? h = 0,875, 2a

Вычисляем значения процесса (Y i ) N=_o

Y o = 0,  Y i = Y i - 1 + щ1 (i

< 9)h + ^ 2 1 (i ^ 9)h + ^Vhe i .

Напомним, что θ распределено по геометрическому закону распределения. Последовательность случайных величин e = (E _i ) N=₁ может иметь три разных распределения.

Случай 1. Стандартное нормальное распределение (как и предполагается в модели).

Случай 2. Равномерное распределение на отрезке [ — 1,1].

Случай 3. Радемахеровское распределение.

В случаях 2 и 3 мы использовали распределения, которые отличаются от модельного.

Проведено M экспериментов. В каждом эксперименте генерировалась значение случайной величины θ, имеющей геометрическое распределение с параметром λ.

Величина ошибки аппроксимации вычисляется по формуле mis =

M

- У

M j=1

N

^ N Y NF(Y j — Y ^j ) ² '

процессы (Y j ) N=o , (Y ij ) N=o соответствуют эксперименту с номером j.

M k ^{1 ,j}             M k ¹ ,

Экспериментальные вероятности qo = MM   Tj0-i, q^ = MM у N—Tj, тj - значение j=1 τ               j=1 τ момента остановки в эксперименте с номером j, k^’j - число Xi = 1, i = 1,..., тj — 1, k^ - число Xi = 1, i = тj,...,N. Процесс (Xi)=o соответствует эксперименту с номером j .

Результаты эксперимента приведены в табл. 1. В первой строке приведены эмпирические вероятности q 0 , q ∞ для каждого рассматриваемого случая. Нетрудно заметить, что эти вероятности приблизительно совпадают с расчетными для данной модели. Напомним, что эти вероятности таковы: q o = 0,875, q ^ = 0,625. Во второй строке приведена средняя квадратическая ошибка аппроксимации. Видно, что самая маленькая ошибка получилась во втором случае. Это произошло потому, что, во-первых, значение стандартной нормальной случайной величины концентрируется в окрестности нуля в то время, как значения равномерной случайной величины распределены по всему интервалу [ - 1,1]. Во-вторых, в третьем случае случайная величина принимает только два значения, 1 и — 1, что, естественно, сказывается на величине ошибки. В третьей строке приведена средняя абсолютная ошибка обнаружения разладки, вычисленная с помощью отношения правдоподобия. В четвёртой строке приведена средняя абсолютная ошибка обнаружения разладки, вычисленная с помощью метода Монте-Карло с апостериорной вероятностью обнаружения разладки. Сопоставление третьей и четвёртой строки говорит о том, что для первого случая ошибка метода Монте-Карло существенно меньше ошибки, полученной в результате использования апостериорного отношения правдоподобия. Во втором и третьем случае наоборот. Этому есть естественное объяснение. Метод Монте-Карло зависит от распределения вероятностей и не обладает робастным свойством.

Таблица 1

Результаты эксперимента

	Случай 1	Случай 2	Случай 3
Эмпирические вероятности q 0 , q ∞	q o - 0,865 q ^ - 0,641	q o - 0,874 q ^ - 0,647	q o - 0,868 q ^ - 0,62
Величина ошибки аппроксимации	0,038	0,017	0,038
Величина ошибки при вычислении разладки детерминированным методом	0,08169	0,07345	0,08658
Величина ошибки при вычислении разладки методом Монте-Карло	0,010139	0,09418	0,10735

На рисунке приведена иллюстрация аппроксимации процесса Y процессом Y . Непрерывная кривая соответствует процессу Y . Прерывистая кривая соответствует процессу Y . Из рисунка можно сделать о хорошем качестве аппроксимации.

Минимизация риска. Рассматривается следующее уравнение: AS n = S n - i (—a) X n , S o = 1, P(X n = 1/n <  9) = q ^ , P(X n = 1/n >  9) = q o , P(9 = j ) = (1 — A)A j ^-1 , j = 1,...

Используются следующие значения параметров: q ^ = 0,8; q _o G { 0,2; 0,3; 0,4; 0,5 } ; A = 0 , 5; N = 10.

Результаты приведены в табл. 2. Во второй строке таблицы приведены оптимальные значения критерия задачи (13) для различных значений q ₀ . В задаче (13) целью является случайная величина £ = SS N +0,01, то есть мы хотим добиться большего по сравнению со стратегией: ≪ В начале купить, в конце продать ≫ .

Приведем интерпретацию полученных результатов. Как уже отмечалось ранее числа, приведенные во второй строке являются оценками сверху вероятностей недостижения цели. Первые два столбца соответствуют ситуации: рост–падение. Падение стоимости акции наступает в момент разладки. Оптимальное поведение в этом случае заключается в покупке акции вначале и продаже ее в момент разладки. Сложность

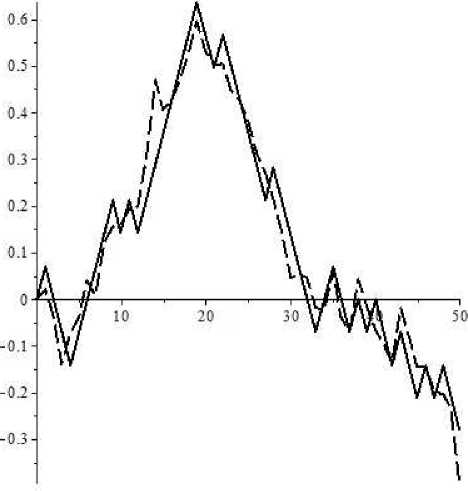
Аппроксимация процесса Y процессом Y

Таблица 2

qo 0,2 0,3 0,4 0,5 Значение критерия 0,0139 0,1213 0,5306 0,9876 реализации такой стратегии заключается в обнаружении разладки. Поскольку предлагаемый в статье метод связан с обнаружением разладки, то вероятности превзойти стратегию ≪вначале купи, в конце продай≫ на один процент равны в первом случае: 0,9782, во втором случае: 0,6876, что тоже неплохо. В третьем и четвертом вариантах тренд стоимости акции после разладки приблизительно равен нулю, поэтому оптимальному портфелю добиться однопроцентного преимущества значительно сложнее.

Заключение

Рассмотрение процессов с разладкой в задачах управления обусловлено воздействием на управляемую систему внешних случайных факторов, изменяющих внутреннюю случайную структуру объекта управления. С такими явлениями приходится считаться в условиях нестабильности, чтобы придать устойчивость развитию объекта управления. Предложенное решение ≪ встроитьfrqq разладку в модель с применением апостериорного подхода, на наш взгляд, является оправданным, по крайней мере, имеет право на существование. В работе рассматриваются бинарные модели управляемых процессов.

Для процессов диффузии естественным способом реализации вычислительного метода является бинарная аппроксимация управляемого процесса. Даже при таком упрощенном способе аппроксимации задача управления становиться NP -полной и рассчитывать приходится на специальные методы ее решения, например, на параллельные вычислительные процессы. Дополнительно к распараллеливанию можно использовать автомодельность броуновского движения и рассматривать задачу управления на фиксированном интервале.

Тем не менее может возникнуть ситуация, когда количество вычислений зашкаливает. В этом случае, при определенных ограничениях на модель возможна редукция

N P -полной задачи к P -полной с потерей информации, необходимой для обнаружения разладки. Один из таких способов предложен в работе, однако, для определения насколько потеря информации сказывается на качестве управления требует дополнительного исследования.

Вычислительные примеры являются иллюстрацией работы предложенного метода, их не следует рассматривать как доказательства чего-либо. Все доводы в пользу предлагаемого метода приведены в остальной части статьи. Экспериментов было проведено достаточное количество с качественно не отличающимися результатами.

Работа выполнена при финансовой поддержке Российского научного фонда (проект № 17-19-01038).