Управление жизненным циклом лактирующих коров на основе вероятностно-статистических и динамических моделей
Автор: Михайленко И.М.
Журнал: Сельскохозяйственная биология @agrobiology
Рубрика: Продуктивность и воспроизвоство поголовья
Статья в выпуске: 4 т.50, 2015 года.
Бесплатный доступ
Проблема воспроизводства поголовья молочного стада в последнее время становится все более острой. Тенденция к его снижению проявляется повсеместно во всех странах с развитым молочным животноводством, а среднее число лактаций по молочному стаду приближается к трем при генетическом потенциале многих пород скота более десяти лактаций. Для решения этой проблемы давно назрела необходимость привлечения самой современной теоретической базы из многих смежных наук. Целью настоящей работы стало теоретическое обоснование первого, ключевого этапа общей концепции управления состоянием здоровья лактирующих коров, предложенной в нашей предыдущей работе (И.М. Михайленко, 2014). На указанном этапе управление заключается в программировании жизненного цикла животных от первой до последней, экономически целесообразной лактации. При этом минимизируется риск отбраковки животных и затрат на их содержание. Такая задача решается впервые в биологической науке. В статье предложены новые динамические модели пожизненных годовых надоев, отражающие возраст животного и потребление питательных веществ в рационах кормления. Важнейшая особенность решения задачи управления жизненным циклом - введение вероятностно-статистических моделей процессов отбраковки коров по состоянию здоровья. Рассматриваются все возможные физиологические состояния коровы, от нетели до последней лактации, и выявляются все потоки и возможные причины отбраковки дойного стада. Эти модели позволяют оценивать риск от возможных потерь поголовья стада, который минимизируется по составам годовых рационов кормления. Разработан алгоритм решения задачи, формирующий последовательность рационов кормления по всем годам жизненного цикла (стратегии кормления молочного скота), которая обеспечивает заданные параметры воспроизводства молочного стада, а также оптимальное число возможных лактаций и оптимальные годовые надои. За счет решения такой задачи достигается нормированное использование лактирующей коровы, обеспечивающее сохранение ее здоровья, при максимально допустимой рентабельности производства молока. В связи с тем, что индивидуальный подход к кормлению коров служит существенным резервом повышения общей рентабельности молочного стада, задача управления жизненным циклом рассматривается как индивидуально, так и в среднем по стаду. Здесь условием для выбора варианта решения задачи служит наличие средств индивидуального контроля за состоянием здоровья животного и дозированием концентрированных кормов и пищевых добавок. Проблема практической реализации предложенной задачи управления в основном связана с отсутствием данных по полномасштабному зооветеринарному мониторингу молочного стада за 10-12 лет, по которым должна осуществляться идентификация математических моделей и апробация алгоритма, разработанного для управления жизненным циклом лактирующих коров.
Молочное животноводство, воспроизводство, концепция управления, состояние здоровья, жизненный цикл, лактационный период, алгоритмы управления, математические модели
Короткий адрес: https://sciup.org/142133608
IDR: 142133608 | УДК: 636/639:636.2.034:51-76 | DOI: 10.15389/agrobiology.2015.4.467rus
Текст научной статьи Управление жизненным циклом лактирующих коров на основе вероятностно-статистических и динамических моделей
Рост продуктивности коров в лучших хозяйствах в ряде областей Российской Федерации, наблюдающийся в последние десятилетия и обусловленный генетическим прогрессом, в целом не сопровождается увеличением продуктивного долголетия и улучшением качества получаемой продукции. По оценкам экспертов, 65 % прибыли в молочном скотоводстве определяется длительностью хозяйственного использования коров. В Канаде она в целом по стране составляет 5 лактаций, в США — 4, на лучших племзаводах Российской Федерации — 3,8, во многих товарных хозяйствах — 2,5 и менее, тогда как оцененный биологический и экономический оптимум — 7-8 лактаций (1-7).
В странах Скандинавии предпринимаются попытки разведения коров, дающих 100 т молока за 10 лактаций. При существующих в нашей стране условиях продление сроков продуктивного использования коров на 6 мес по экономическому эффекту эквивалентно увеличению численности дойного стада на 12 %. То есть имеется значительный ресурс для повышения эффективности молочного скотоводства за счет роста пожизненной продуктивности коров (8, 9).
Потери от недополучения ремонтного молодняка в молочном животноводстве занимают одно из первых мест среди всех экономических убытков. Кроме того, от каждой бесплодной коровы хозяйство недополучает минимум 25 % ее удоя за лактацию. К этому нужно добавить расходы на лечение, на многочисленные безрезультатные осеменения и потери, связанные с преждевременной выбраковкой ценных, часто молодых, коров (10).
В нашей предыдущей работе (11) была дана общая характеристика проблемы воспроизводства в молочном животноводстве — центральной в этой важной отрасли для всех стран с развитым сельским хозяйством. В этой связи предлагалась общая концепция управления состоянием здоровья животных (8). В соответствии с ней целью управления должно быть не достижение максимальной продуктивности, как сейчас повсеместно принято, а максимизация прибыли, получаемой за все время жизни животного. Эта цель может быть достигнута при соблюдении трех взаимосвязанных требований: обеспечения прохождения всего жизненного цикла от первой до последней генетически возможной и экономически целесообразной лактации; получения условного максимума прибыли по каждому лактационному периоду всего жизненного цикла; индивидуальной коррекции условного максимума прибыли для коров и стада в реальном времени.
В настоящей работе рассматриваются теоретические основы решения задачи по управлению жизненным циклом. При этом в зависимости от технической и технологической базы конкретной фермы возможны два подхода. В первом случае, когда такая база позволяет учитывать состояние здоровья каждой коровы, осуществляется управление индивидуальным жизненным циклом. Оно достигается даже при отсутствии полномасштабного персонального кормления животного и без создания для него специальных условий содержания, то есть только за счет индивидуальной дозировки концентрированных кормов, витаминов и премиксов. Во втором случае, когда оценка состояния здоровья осуществляется выборочно и этот показатель определяется в среднем по стаду, дополнительно возникает необходимость управлять жизненным циклом в среднем по стаду.
Основное условие реализации полного жизненного цикла коровы — сохранение репродуктивной функции, которая может быть утеряна из-за неадекватного ухода и кормления и, как результат, возникающих болезней и патологий. Чаще всего причинами отбраковки лактирующих коров оказываются нарушения обмена веществ, болезни пищевой системы, вымени, половых органов, послеродовые осложнения, маститы, болезни суставов и другие заболевания, связанные с особенностями кормления и содержания животных. Всего насчитывается более 20 видов заболеваний, приводящих к отбраковке коров и прекращению их жизненного цикла (10).
Поскольку появление любой патологии носит вероятностный характер, наступление очередной лактации рассматривается как случайное событие (продолжение индивидуального жизненного цикла). Это приводит к тому, что в общем стаде формируются случайные потоки животных, переходящих из одного состояния в другое (рис.). Из всех возможных состояний нас интересуют только те, на которых вероятна отбраковка, в результате чего жизненный цикл животного обрывается и изменяется структура стада.
Введем обозначения отбраковочных потоков λ:
из состояния s = 2 (нетели) — λ 26 ( t , Z 26 );
из состояния s = 3 (сухостойные) — λ 36 ( t , Z 36 );
из состояния s = 4 (новотелы) — λ 46 ( t , Z 46 );
из состояния s = 5 (лактирующие) — λ57(t, ρ57), где λij(t, Zij) — число отбракованных коров в единицу времени (сут), которое обычно рассматривается как интенсивность отбраковки; Zij — нозологические векторы отбраковки, включающие все виды заболеваний, свойствен- ные соответствующему состоянию и приводящие к отбраковке; ρ57 — пра- вило, по которому осуществляется вывод лактирующих коров из оборота.
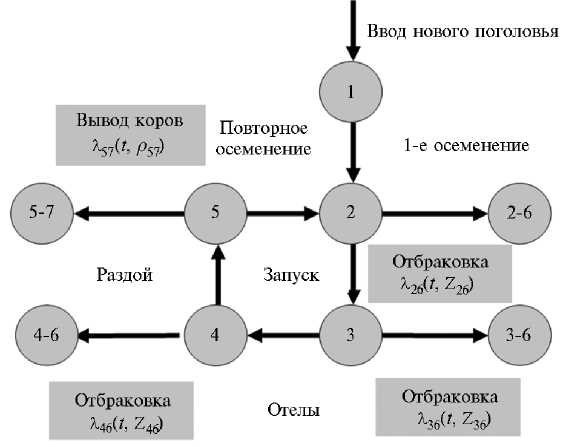
Граф-схема оборота поголовья в стаде: 1 — телки, 2 — нетели, 3 — сухостойные коровы, 4 — новотелы, 5 — лак-тирующие коровы, 6 — отбракованные коровы, 7 — коровы, выведенные из оборота по критерию эффективности.
Если формирование потоков отбраковки в состояниях s = 2, 3, 4 — это результат несовершенства и неадекватности управления состоянием стада в среднем, то формирование отбраковочного потока лак-тирующих коров (s = 7) — локальная компонента управления, напрямую ориентированная на получение дополнительной прибыли.
Общие алгоритмы управления жиз- ненным циклом лакти-рующих коров. При индивидуальном управлении жизненным циклом лак- тирующей коровы следует иметь в виду, что из всех состояний, в которых может находиться животное, для критериальной оценки наиболее важны s = 5 (лактация) и s = 6 (отбраковка). Каждое из этих состояний случайное и зависит от состояния здоровья животного. Поэтому индивидуальное управление жизненным циклом отдельного животного должно минимизировать риск потерь, связанных с ненаступлением очередной лактации.
Выражение для риска управления состоянием здоровья отдельного животного выглядит следующим образом:
∗ п -1
^(n ∗ ,ий)= х [^-(i-^cz^-c^ncu1 n ) -r(U 1 n^"Рп№к , 1 n 1 n
И = 1
П (U) где n = 1, 2, …, n* — номера лактаций (от первой до последней, экономически целесообразной); Mn∗— заданная программа получения прибыли от одной коровы по всему жизненному циклу; сn — прогнозы цен на молоко, П(U1n) — годовые надои по всему жизненному циклу (функция вектора управления U1n, компонентами которого служат расходы всех видов питательных веществ в рационах кормления); pn(Z) — вероятность отбраковки коровы на n-й лактации, зависящая от вектора заболеваний Z; r(U1n) — годовые затраты на содержание коровы (функция вектора управления U1n); сk — стоимость отбраковываемой коровы; Пn∗— генетическая программа продуктивности соответствующей породы. Выражение [1] представляет собой взвешенную по вероятностям состояний разность между доходами, полученными на момент отбраковки (n = n*), и ущербом от потери животного при его отбраковке. Достижение поставленной цели управления жизненным циклом коровы соответствует минимизации риска по числу лактаций n* и последовательности векторов управления по всем лактациям: , пй(и)^п^й<0,5;^ = 1=0 . При управлении жизненным циклом «в среднем по стаду» выражение для риска управления будет иметь следующий вид: _ и* — 1 _ _ _ ~ ^(^ ’U ) = Т, \м ~ ^—рА//У Anj\//1W(u УЛ-с^рА^члУ Гг 1 7l 7l 7lJ И ИХ 1n 1n кп тг, n n [3] Пи(ии)-Пи;^<0’5;^ = 1=0 , где Pn(Z) — вероятность ненаступления n-й лактации в среднем по стаду (отбраковки), определяемая вектором заболеваний Z для состояния з∼доро-вья «в среднем по стаду»; n — средний по стаду годовой надой; 1n — средний п∼о стаду вектор управления в соответствующий лактационный период; r(u1n) — средние по стаду затраты на рацион. Как и для задачи индивидуального управления жизненным циклом, достижение поставленной цели при управлении «в среднем по стаду» соответствует минимизации критерия [1] по числу циклов и последова- тельности векторов управления в отдельные лактационные периоды: R(n*, U )------------------------->min , 1n * ' 1n 1n = 1 1n = n Пй(ий)<П*; /?й<0,5;^й = 1=0 . Решением задач [2] и [4] является последовательность векторов управления для всех периодов лактации U1n и U1n, а также оптимальное число лактаций n*. В этой связи потребуются математические модели, учитывающие все параметры состояний, по которым оценивается риск управления жизненным циклом. Как показывает анализ отечественных и зарубежных публикаций, ничего подобного пока не представлено (12-27). Основная направленность в таких разработках — создание аппроксимирующих функций, максимально отражающих форму лактационных кривых, однако они непригодны для решения задач управления. Ниже предложены новые модели, отражающие возрастную динамику коров и процессы их отбраковки. Модели индивидуальных и средних по стаду пожизненных надоев: Πn + 1 = aΠn + bTU1n + cTf[n], n∈ (1,n* - 1), Π(1) = Π0; fT[n] = [n n2n3], U1n = НRn, где Π — годовые надои, кг; U1 — вектор питательных элементов, расходуемых за год, R — вектор кормовых компонентов (рацион), H — матрица содержания питательных элементов в кормовых компонентах; fT[n] = [n n2 n3] — вектор функций времени, учитывающих возраст животного. Модели вероятности индивидуальной и средней по стаду отбраковки коров: Xn = DUn, Yn = Xn -∆, Cn = WYn, и п = О, если р = hTC <5 ; z z п 2 = z , если р = (hT С ) > 6 ; FZ 'Z Z П^ Z ’ * п=п ^СЛИ-^^О; . Рп^ = Е р^ , [7] S = 1 где Xn — вектор параметров состояния здоровья лактирующих коров на n-й лактации (среднее значение вектора состояния здоровья в интервал периода лактации Xn); Yn — вектор диагностических признаков, равный размерности вектора параметров состояния здоровья; ∆ — вектор допустимых значений показателей состояние здоровья, отклонения от которых служат диагностическими признаками; Cn — вектор патологических синдромов, представляющий собой линейную комбинацию векторов диагностических симптомов; W — матрица линейных комбинаций диагностических симптомов; h — векторы дискриминантных функций обнаружения заболеваний, ведущих к отбраковке коров; P{(hTz Cn⋅t∑) ∈ ΩZ} — вероятность попадания значений дискриминантной функции в область допустимых значений; t — суммарное время превышения параметром состояния здоровья допустимых значений; ΩZ — области допустимых значений дискриминантных функций обнаружения заболеваний. Алгоритм индивидуального решения для животного. Смысл задачи заключается в минимизации риска ∗ 77* -1 R 11 И = 1 П 11 /7 77 77 77 и k [8] П .(U) 77 7 77 77 77 = 1 для следующей динамической системы: Πn + 1 = aΠn + bTU1n + cTf[n], n ∈ (1,n*- 1), Π(1) = Π0; [9] fT = [n n2n3], U1n = НRn. Гамильтониан системы [8], [9] имеет вид: H=^-d-pAmc n(R )-C^RJ—Lр(Z )с,) + И И /7 77 77 к И * И П К +А(аПи+ЬТ HR^+c1^/?]), модель сопряженной переменной — соответственно дН А , --R = -aX +(1-р (Z)c ) й + 1 ЭП п 77 х 77 , а смысл оптимизационной задачи заключается в минимизации критерия [8] посредством использования гамильтониана [10] и сопряженной переменной [11]. Подробный алгоритм такого решения приведен ниже. В описанной задаче исходной информацией служат программа получения прибыли по лактациям Mn∗ , цены на молоко по лактационным периодам cn, стоимость самих коров сk, цены на корма и кормовые добавки, по которым определяются затраты на кормление по лактациям i(U1a), параметры математических моделей a, bT, cT, hT, 5Z. Кроме того, здесь имеются «фазовые» ограничения по состоянию здоровья, задающие генетические ограничения и возможность отбраковки: . 1и п п Z7 = 1 С учетом последних замечаний задача оптимизации индивидуального жизненного цикла животного имеет следующий вид: Я(»’,кп)= S [М*-(1-Р„(2))' /7 = 1 •(^Д, (R7 ) - ''(к 7))] - -Pn(Zn) ck ------------->min Rp - R^» e^\ . Пошаговый алгоритм. Опишем полученную последовательность действий при решении задачи. Шаг 0. Задаются циклическая переменная алгоритма i = 0, начальная длительность жизненного цикла, то есть предельно возможное число лактаций ni*, начальная программа «пожизненного кормления» животных в виде последовательности векторов рационов Rni, n = 1, 2, …ni* и последовательность вероятностей отбраковки pni. Шаг 1 для i = 1. Для интервала n = 1, 2, …n* решается система: Пn + 1,i = aПn,i + bTU1n,i + cTf[n], ; fT[n] = [n n2n3], [13] U1n,i = НRn,i; Xn,i = DUn,i, далее вычисляется последовательность вероятностей отбраковки по всем лактациям Y ■ = X ■ - A n,i n,i - ∆, C = WY ■ Сn,i W n,i, , np znp z np z , z+l . ИЛ z z ,=z , если p . = (hT C .)>5 up n znp z np z , z N: p -(z)= E p\- ) np /i n z = 1 Шаг 2. Решается в обратном времени уравнение для сопряженной переменной по каждой лактации: ЭН . ) , [15] ne (nz*+i,1); x^7/+J=0 , формируется массив решения ХЛ;7. Шаг 3 для i = 1. Вычисляются частные производные гамильтониа- на по вектору рационов по каждой лактации: эн . . n,z dR vn,i R n,i Шаг 4 для i = 1. Уточняется последовательность векторов рационов по лактациям: RR И,1 + 1 п,1 П,1 И,1 Пр+1 RR , далее — переход к шагу 1. Шаг 5 для i > 1. Вычисляются частные производные гамильтониана по вектору рационов по лактациям: = (1-^ .(Z))Cr + A .НЧ+ . Шаг 6 для i > 1. Уточняется последовательность векторов рационов: R И,1 +1 R Z ; n,i nj nj п,1 + 1 — и и R R ∗ далее — переход к шагу 2, если Rni > 5p; в случае, когда это условие не выполняется, процесс завершается. Результатом решения задачи являются последовательность оптимальных годовых рационов по всем периодам лактации R∗n , предельное число лактаций n* и оптимальные годовые надои Πn*, которые используются в качестве интегральных ограничений в процессе управления каж- дым лактационным периодом. Алгоритм решения задачи управления жизненным циклом коров в среднем по стаду отличается от алгоритма индивидуального управления только переменными состояния. В результате, кроме средних по стаду оптимальных годовых рационов кормления по всем периодам лактации R∗n и оптимальных средних годовых надоев П„, получают ожидаемое число выбытия коров Nn = pn(Z)N, где N — общее поголовье стада на ферме, и общий риск по дойному стаду (n*). В связи с тем, что в статье раскрывается только общий теоретический подход, мы не описываем содержания всех векторов состояния и управления. Нагляднее всего показать это на практических примерах, что будет сделано в последующих работах. Таким образом, обоснована теория управления жизненным циклом лактирующих коров. Она заключается в минимизации риска потерь от отбраковки животных и затрат на их содержание. Теория базируется на новых динамических моделях годовых надоев и вероятностно-статических моделях процессов отбраковки коров по болезни и экономической целесообразности. По своей сути решение этой задачи позволяет получить научно обоснованные нормы кормления животных по всем лактациям жизненного цикла, обеспечивающие заданный темп воспроизводства. Про- блема практической реализации предложенной теории заключается в отсутствии информации (мониторинга) о состоянии здоровья животных в течение длительного периода (не менее 10 лет) в зависимости от фактических рационов кормления. Это связано с утратой соответствующих функций современной ветеринарной службой хозяйств. Ситуация может быть исправлена только созданием опытной модельной молочной фермы на 100150 гол., оборудованной всеми необходимыми системами мониторинга за состоянием здоровья лактирующих коров и биохимическим составом всех компонентов используемых кормов. Идентификация предложенных математических моделей по мониторинговой информации позволит реализовать на практике задачу управления жизненными циклами лактирующих коров и тем самым решить проблему воспроизводства поголовья дойного стада. Л И Т Е Р А Т У Р А ФГБУН Агрофизический институт, Поступила в редакцию 195220 Россия, г. Санкт-Петербург, Гражданский просп., 14, 28 августа 2014 года Sel’skokhozyaistvennaya biologiya [Agricultural Biology], 2015, V. 50, ¹ 4, pp. 467-475 NEW PROBABILISTIC STATISTICAL AND DYNAMIC MODELS TO CONTROL LIFE CYCLE IN LACTING COWS
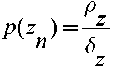
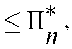
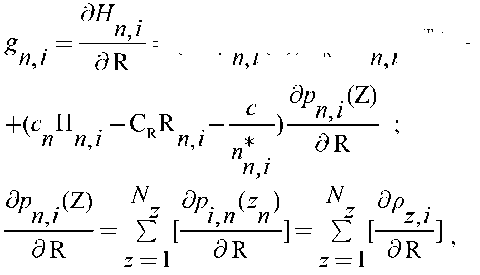
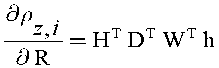
Список литературы Управление жизненным циклом лактирующих коров на основе вероятностно-статистических и динамических моделей
- Ferris T.A., Mao I.L., Anderson C.R. Selecting for lactation curve and milk yield in dairy cattle. J. Dairy Sci., 1985, 68: 1438-1448 ( ) DOI: 10.3168/jds.S0022-0302(85)80981-4
- Oltenacu P.A., Rousaville T.R., Milligan R.A., Foote R.H. System analysis for designing reproductive management programs to increase production and profit in dairy herds. J. Dairy Sci., 1981, 64: 2096-2104 ( ) DOI: 10.3168/jds.S0022-0302(81)82813-5
- Haile-Mariam M., Goddard M.E. Genetic and phenotypic parameters of lactations longer than 305 days (extended lactations). Animal, 2008, 2: 325-335 ( ) DOI: 10.1017/S1751731107001425
- Kirkpatrick M., Lofsvold D., Bulmer M. Analysis of the inheritance, selection and evolution of growth trajectories. Genetics, 1990, 124: 979-993.
- Meuwissen T.H.E. Optimization of dairy cattle breeding plans with increased female reproductive rates. Thesis. Research Institute for Animal Production «Schoonoord», Wageningen, 1990.
- Oltenacu P.A., Rousaville T.R., Milligan R.A., Foote R.H. System analysis for designing reproductive management programs to increase production and profit in dairy herds. J. Dairy Sci., 1981, 64: 2096-2104 ( ) DOI: 10.3168/jds.S0022-0302(81)82813-5
- Vargas B., Koops W.J., Herrero M., Van Arendonk J.A. Modeling extended lactations of dairy cows. J. Dairy Sci., 2000, 83: 1371-1380 ( ) DOI: 10.3168/jds.S0022-0302(00)75005-3
- Михайленко И.М. Системные основы точного животноводства. В кн.: Точное сельское хозяйство (Precision Agriculture). СПб, 2010: 321-336.
- Trofimov A.A., Chugin I.V. Modeling turnover herds of cattle and optimal planning of the production of farms. In: Simulation of innovation processes and economic dynamics. Moscow, 2006: 212-225.
- Справочник по ветеринарной медицине/Под ред. А.Ф. Кузнецова. СПб, 2004.
- Михайленко И.М. Автоматизированные системы управления здоровьем животных как стратегическая основа оптимизации воспроизводства в молочном скотоводстве. Сельскохозяйственная биология, 2014, 2: 50-58 ( , 10.15389/agrobiology.2014.2.50eng) DOI: 10.15389/agrobiology.2014.2.50rus
- Dijkstra J., Lopez S., Bannink A., Dhanoa M.S., Kebreab E., Odongo N.E., Fathi Nasri M.H., Behera U.K., Hernandez-Ferrer D., France J. Evaluation of a mechanistic lactation model using cow, goat and sheep data. J. Agr. Sci., 2010, 148: 249-262 ( ) DOI: 10.1017/S0021859609990578
- Grossman M., Koops W.J. Modeling extended lactation curves of dairy cattle: a biological basis for the multiphasic approach. J. Dairy Sci., 2003, 86: 988-998 ( ) DOI: 10.3168/jds.S0022-0302(03)73682-0
- Jaffrezic F., White I.M.S., Thompson R., Hill W.G. A link function approach to model heterogeneity of residual variances over time in lactation curve analyses. J. Dairy Sci., 2000, 83: 1089-1093 ( ) DOI: 10.3168/jds.S0022-0302(00)74973-3
- Macciotta N.P.P., Dimauro C., Steri R., Cappio-Borlino A. Mathematical modelling of goat lactation curves. In: Dairy goats feeding and nutrition/A. Cannas, G. Pulina (eds.). CAB International, Wallingford, UK, 2008: 31-46.
- Congleton W.R. Jr. Dynamic model for combined simulation of dairy management strategies. J. Dairy Sci., 1984, 67: 644-660 ( ) DOI: 10.3168/jds.S0022-0302(84)81350-8
- Dijkhuizen A.A., Stelwagen J., Renkema J.A. A stochastic model for the simulation of management decisions in dairy herds, with special reference to production, reproduction, culling and income. Prev. Vet. Med., 1986, 4: 274-289 ( ) DOI: 10.1016/0167-5877(86)90010-3
- Guo Q., White R.E. Cubic spline regression for the open-circuit potential curves of a lithium-ion battery. J. Electrochem. Soc., 2005, 152: A343-A350 ( ) DOI: 10.1149/1.1845336
- Leon-Velarde C.U. A simulation model to analyze the bio-economic function of cows in intensive dairy farms using a systems approach. Thesis Ph.D. University of Guelph, 1991.
- Mayer D.G., Belward J.A., Burrage K. Use of advanced techniques to optimize a multidimensional dairy model. Agricultural Systems, 1996, 50: 239-253.
- Oltenacu P.A., Milligan R.A., Rounsaville T.R., Foote R.H. Modelling reproduction in a herd of dairy cattle. Agricultural Systems, 1980, 8: 193-205.
- Quiroz R., Arce B., Cañas R. Aguilar C. Development and use of simulation models in animal production.systems research. In: Animal production system research; methodological and analytical guidelines. IDRC/IICA-RISPAL; San José, C.R., 1994: 103-149.
- Wilson D.J., González R.N., Hertl J., Schulte H.F., Bennet G.J., Schukken Y.H., Gröhn Y.T. Effect of clinical mastitis on the lactation curve: a mixed model estimation using daily milk weights. J. Dairy Sci., 2004, 87: 2073-2084 ( ) DOI: 10.3168/jds.S0022-0302(04)70025-9
- White I.M.S., Thompson R., Brotherstone S. Genetic and environmental smoothing of lactation curves with cubic splines. J. Dairy Sci., 1999, 82: 632-638 ( ) DOI: 10.3168/jds.S0022-0302(99)75277-X
- Wang Z., Goonewardene L.A. The use of MIXED models in the analysis of animal experiments with repeated measures data. Can. J. Anim. Sci., 2004, 84: 1-11 ( ) DOI: 10.4141/A03-123
- Vetharaniam I., Davis S.R., Upsdell M., Kolver E.S., Pleasants A.B. Modeling the effect of energy status on mammary gland growth and lactation. J. Dairy Sci., 2003, 86: 3148-3156 ( ) DOI: 10.3168/jds.S0022-0302(03)73916-2
- Sorensen A., Muir D.D., Knight C.H. Extended lactation in dairy cows: effects of milking frequency, calving season and nutrition on lactation persistency and milk quality. J. Dairy Res., 2008, 75: 90-97 ( ) DOI: 10.1017/S0022029907002944


