Управляемость, наблюдаемость, стабилизируемость нелинейных систем

В связи с интенсивным развитием промышленности, электроэнергетики, теории нелинейных колебаний, автоматического регулирования, оптимальных процессов развивается теория сингулярно возмущенных дифференциальных уравнений и ее методы активно применяются для решения задач из различных областей естествознания и техники. Для анализа нелинейных разнотемповых систем применяется метод декомпозиции, основанный на теории интегральных многообразий быстрых и медленных движений. Декомпозиция подразумевает частотное разделение движений на быстрые и медленные. Данная работа посвящена изучению свойств управляемости, наблюдаемости, стабилизируемости трехтемповой нелинейной автономной системы.

Цель работы:

• •    Понижение размерности задачи управляемости, наблюдаемости и стабилизируемости нелинейной трехтемповой автономной системы так, чтобы модель меньшей размерности с большой степенью точности отражала все свойства исходной системы.

• •    Получение достаточных условий, управляемости, наблюдаемости и стабилизируемости сингулярно возмущенных систем.

РАСЩЕПЛЯЮЩЕЕ ПРЕОБРАЗОВАНИЕ

Рассмотрим модель трехтемповой системы вида:

су — а_г (у, z, у, z, е, ц) = Ь_т (у, z, е, д)и,

E[iz — а₂ (у, z,y, z, е, ц) = Ь₂ (у, z, е, p.)u,

где – переменные состояния, – управляющие воздействия, – измеряемая координата, – векторные функции, – матричные функции соответствующих размерностей, равномерно непрерывные и ограниченные с достаточным числом частных производных по всем аргументам,    – малые положительные параметры, е Е (0, е0],^ Е (O,go],t Е К.

Введем обозначения,               Полу чим трехтемповую систему:

у = X_vz = Х_г,ЕХ_г = а₁(у,2,Х₁,Х₂,£,д)

+ ^^,2, E,fl)u, ЕЦХ_г⁼ О-2^У'²’^Х1'^Х2’^Е’Н)

Пусть для системы (2) выполняются следующие условия [1,2]:

Уравнение                       имеет изолированное решение

В области

11^2 - h-^b.z.x^) || <  р₂,е Е (0, е₀], /z £ (О,д_о]}

,   ...... ,(о,о)                   _ функции            имеют достаточное чис ло равномерно непрерывных и ограниченных частных производных по всем переменным.

Собственные значения

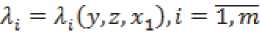
матрицы

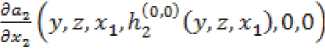
удовлетворяют неравенству

При выполнении таких условий система у = xvz =х2,ех1 = a1(y,zrx1,x2,E,li), имеет интегральное многообразие медленных движений л- = :: д z .v j .. ■ В движение по которому описывается системой

У = XpZ = h,₂(y,Z,Xp£,fl),EX₁ =

= Я^ (у, Z,Xph₂(y, Z, Хр£, fl),E, ц). (3)

Пусть для системы (3) выполняются следую щие условия:

1’) Уравнение

: у- - z V ; = : имеет

г(о,о)г '

изолированное решение л = ■: У -

2’) В области nt = {(у,^хре,д): 1%! - h^ (y,z)|| < pve е (o.zj,д е (o,gj,

-_ г- .._    ..- . функции ;, <      •:- имеют достаточное число равномерно непрерывных и ограниченных частных производных по всем переменным.

3’) Собственные значения .\ = .\ 'v z- . й, (О,О) г

= _ - датри     —ыу, 2, гц т (0,0)^ т (0,0) / x « — x ■д у 2 у 2- - - ■ удовлетворяет неравенству Р-£ .'. 1 -£■_ < В.

При выполнении таких условий система (3) имеет интегральное многообразие медленных движений л = < у 2 _- Функции ■: ■:- определяют интегральное многообразие самых медленных движений х_т = ^(v^Vq, е,ц),х₂ = h,₂(yQ,VQ, ^;: У- ■ г г г .. ■ , движение по ко -торому" описывается системой У = ^(v^v^s.^.z = ^(у^г^к^.г^Е,

■ i .. ■. Используя метод декомпозиции [4], основанный на теории интегральных многообразий, произведем расщепление управляемой системы (2). Произведем замену переменных вида У = Vo¹ + ^£Hoto + ^£P^Hoto.^z = ^vo + ^£Hoto + ^£Р^но(2}-

%_t = v₁ + ^ + fiHpX₂ = v₂ + h₂.

В результате такой замены, получим систему блочно-треугольного вида:

Vq = h^.V^E,^) -

+ S1(v^v02,v1,v2,e,^)u,£^v2 = A2(Vq, Vq , Vp V2, E, fl) + B2 (Vq , V^, E, fl)u,W =

= у py у у у j .. ■ (4)

где Ji = ajCy^.y^.Vj -М^с ^Т'^)' ^(Уо-Уо-¹⁷! + ^1,£,д),Е,д) - a^y^.y^.

^hi (Уо- У о -^Е-1¹)- ^hi (Уо- Уо- ^ki' ^Е- В)-^Е- Р) ~

Shi Г7 Z 1   2 I 7 Z 1   2

• - ^£ ^Г ^vi - ^£^| [^2(Уо^Уо^^vi + ^fci(Уо^Уо

Е, fl), Е, fl) - h₂ (Уо,Уо- hl (Уо-Уо -^Е- н). Е. д)],Л₁(г_о¹,р_о²,О,е,д) = 0,A₂Vvq,v^,v_vv₂, Е, fl) = а₂ (Vq¹ + EH^_to + EflH^.V^ + Е ■ ^ti0(2) + ^Ho^yi + ^1 + цН^, v₂ + h₂, е, fl) - ^(Vq¹ + sH^Y) + EfiH^_to.Vo + eH^₂-) -VsiiHq^,^ + 7^ + fiH^,h₂,s,fi) — £Д^ ■ ^V2 -^5^ (^ai(^vo + ^£//0(D + ^EHH_oto,v_o +^£ti0(2) + ^£^0(2),^vi + h-t + fiH^,v₂ + h₂, E,fi) - g^Vq + EH^_to + EfiH^.v^ + ^eH Oto + ^E^^H 0(2}- ^V1 + ^hi + pH^,h₂,s,fi), A₂(yo,Vo,v_vO,E,fi) = 0,B₂(v^,v^,e,/i) = = ^(Vq¹ + £H^_to + EflH^.V^ + EH^_a + ЕЦН0(2}-^E-P-) ~ H ^ ^1(Vq + EHod) + E ■ B^HOto- ^V0 + ^S^0(2) + EflH^.E,^)^! =

= ^(Уо.Уо.Е.^-^В^.^.Е,!!)^ = Vq¹ + ^еНо(1}.Уо = W + ^£^0(2)-

Функции л-" . /=22 л " равномерно непрерывны и ограничены с достаточным числом частных производных по всем аргументам. Функции Н" . ■:. / = 2 _ л" можно искать в виде асимптотических разложений [5]

Vq , Up fl), H^ (y^, Уо, У!, V₂, E, fl) = 5_k>₀ ^//^(yo^yo^yi, V₂, Е), Но^ОУо-Уо-У!-^-⁵-^) = = T._k>₀B^kH^_k(y^y^ypV₂,E),i = 0,1;

; ■: = '.': - йл-" . ; = 2 2 из соответствующих уравнений

3h2     ,     8h2 , ,              x .3h

Efl—^XT + Eft —^h2Vy,Z,XpE,fl) +{1—^ -dy         dzdx^

Shi 7 Z 1   2 X 1 Shi 7 z 12

^£5^ Ь1(Уо -Уо -E,fl) + E-^h₂(y₀ ,y₀ , hi(yo,yo,E,fi),E,fi) = ^(Уо^УоЛгСУолУо²,

Е, Р). ^2 (Уо'Уо. ^к1(Уо.Уо. ^£. Р). Е, Д), Е, р)

^^НоСр 7 ( I 2 Л I ^Н^^ 7 Г I 2 е-гч-П1(^₀,г₀,е,д) + е — —n₂(v₀,v₀

dv0                         dv0

^1 (Vq, V², E, fl), E, ц) + -^-л ! (Vq¹, V_o², V_v s, д) = Д^,; = 1,2; Д^ = ^(УолУо^^д) -^(т^т^дХД^ = /1₂(Уо,Уо,^1(Уо, у², Е, fl), Е, ц) - h₂ (Vq , Vq , И_г (Vq, v², Е, д), х ^fl. <12 X . ^ЭНО(П

Е,Р); ец-^-п^о.Уо.Е.ц) + ЕЦ-^--

Л₂ (Уо, Уо ^ ^vi + ^Л1 (Уо - Уо» е, р), е, д) + Д ■ ^^“1 (Уо-Уо- ^vi + ^к1 (Уо- Уо- е, р\ h₂ (уд¹, y₀²,Vi + &!б£,у£б,д),8,д),6,д) + ^£' Л₂(у₀¹,г^,у₁,у₂,£,д) = ^/ = ^2; ДЬ1 = M^vo + s^od) + £pH§_w, и£ + еН^ +

ЕрН^.Е.р) - ^(Уо.Уо.Е.р); ^ДМ = A₂(Vq + £^₍i) + spH^.v^ + еН^) + £ ■ дЯ₀²₍₂₎,171 + ^(v^ + eH^_w + ед//^^, Vq + ^£^q(₂) + £ДЯ^₍₂),£,д),£,д) - h₂(y£,y£, ^vi + ЬхСУо.Уо.Е.кО.Е.^У.ЕР^М^о.Уо» Е, ц) + £Д ^ к₂(Уо.Уо. Ч + ^(Уо.Уо. Е, р). Е, д) + Д ^ ^а1(У0'У0' ^vi + ^(Уо-Уо» е,р")Л₂1Уо.Уо.^т1 + ^(Уо-Уо.е.рУе.Р^.е,

а

д) +

дН, л /■ 1   2                >        z 1 1

^Л2(г0,г0,г1,р2,£,/1) = a^Vo +

eHq_W + eilH^.v^ + £^(2) + ЕрН^,17_г +ЬМ>Уо.Е,р) + gH^,V₂ + ^(Vq¹ + £ ■

#0(1) + ецН^.г^ + eHq^ + £ДН₀²₍₂₎,Г₁ +

+^1(Уо,Уо,^£,д) + д#1,^£,д),^£,д) - ^а1(Уо у², v_t + h_t(Уо.Уо, Е,р), £,р),h₂ (уд,у², г_г + hl (Уо, Уо. Е, р), E, р), Е, р).

УПРАВЛЯЕМОСТЬ И НАБЛЮДАЕМОСТЬ

Рассмотрим задачу о приведении системы (4) из некоторой окрестности начала координат в начало координат с помощью гладкого управления. пусть . : = : с ■ = ; = : 2. Линейная модель для системы (4) в окрестности начала координат имеет вид:

v₀ = Л_ог_о + B_ou,v_o = (v^v²)';

ег₁ = A₁v₁ + В^; spv₂ = A₂v₂ + B₂u;

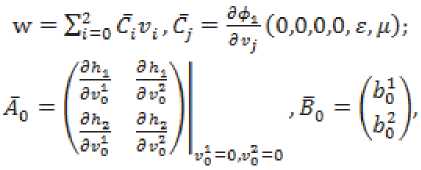
ЭН1 г л

^Ьо ⁼ — (0.070,0, £,/х)В₂ (ОД £,/1),1

1,2; В, = В, (0,0,0,0, Е,ц),Вп = S₇(0,0, е, piYA, = ^(0,0,0,£,д),Л₂ = ^(0,0,0,0,

E»P).j ⁼ 0,1,2.

Используя подход, предложенный в работе [6], можно доказать следующие утверждения.

Теорема 1. Рассмотрим модель управляемого процесса (4) с ограничивающим множеством v. ^ У/ содержащим внутри себя точку :. = ". Предположим, что: 1) ^(ОД^д) = 0, fi₂(0,0,/i₁(0,0, £,д), е, р,) = 0;2) rank (В₀,А₀В₀ .....Л^^^^Во)

= ^ + п₂; 3) rank ^В^А^В^...,^^{1 1}В^

= ■; : = 2 2. Тогда существуют такие ;' :- 2 ..' :- 2 что при всех £ е (О,е*],£* <  £₀,р € (О,д*],д? < д₀.

область :- нуль-управляемости открыта в 71" ■-^- ■= (т.е. система (4) локально управляема вблизи нуля).

Теорема 2. Рассмотрим модель наблюдаемого процесса (4) в 71" ' -“'■: , Пусть функции системы (4) непрерывно дифференцируемые в окрестности точки '.'-; = 2 ■. -" = 2 с = 2 с- = 2 :. = 2 с входными сигналами -- : _- .. ■ 2 £ 7 7 2 в -■! и выходными сигналами Ф1 ^(t,E,[l), Vq (t, Е, р.), V_x (t, Е, р.), V₂ (t, Е, р), Е, pt)

в Предположим, что 1) ^(0,0,£,д) = О.^^.ОЛ^О.О.Е.^.Е.р) = 0;

• 2.    С тс 7- 7- .. 7- ■- :- - 7- = : - :_:;

• 3)    rank (С',А'С', ..., (A')”i"¹C_i') = n_ir i = 1,2.

Тогда существуют такие" ": -    ": - что при всех

Е Е (0, £*],£* < £о,д Е (О,д*],д* < д0, система (4) локально вполне наблюдаема вблизи начала координат.

СТАБИЛИЗИРУЕМОСТЬ

В системе (4) выберем управление следующим образом: 5 с-" с-" с с- _■ .. ■:. = -A^v^v^v^e,^") + А^^Лг^^г^е, Ю и = -Л2 (t’o , t^, i^, f:, E, н) - A;; v:, где матрицы .4 : = 2 2 произвольные гурвицевы матрицы [7], соответствующие уравнениям Ля- пунова с положительно определенным решением Рр т.е. д;л+ми = -1,1 = i,2. Следовательно, собственные значения Хк,к = 1,пг матриц Д^ имеют отрицательные вещественные части, т.е. удовлетворяют неравенствам ReXk<-pk<0. Подставим выбранное управление в результирующую систему (4):

Vq = h^v^.v^.E.p) - ^^(-^(v^v^, vv v2 ,£,//)+ Л Z2 v2 ), v2 = h2 (Vq1, v 2, hl(vq,Vq, £,P)»E,P) - ^7^(-^2Oo-uo-

Vp^^^) + ^22V2)^1 = A1VP ^2 = Л22и2. (5)

Исследуем устойчивость системы (5). Движение по интегральному многообразию v_± = 0, v₂ = 0, самых медленных движений системы (5), описывается системой Vq = ^(v^V^E,^),^ = h₂(v^,V^, ^(^^.Ел^лЕлД). Следовательно, система (5) сводится к системе блочно-диагонального вида Vq = h^V^r^E,^, Vq = ^2 C^' V ², h_T (v£, V 2_{л E;} д)_{л E;} p^, ЕР_г =А₁₁г₁,ецг₂ =A₂₂v₂, две быстрые подсистемы которой асимптотически устойчивы. Итак, задача устойчивости системы (5) сведена к задаче устойчивости на интегральном многообразии.

ПРИМЕР

Рассмотрим систему P нелинейных осцилляторов [8]:

ex_l + а,х? + b_ix_i = Y[U,i = l,n;

E^Xj + CjXj^xJ - 1) + djXj = Yj-u-j = n + 1, p; z = S^=1 hkxk, где коэффициенты

a_if bp Cj, dj, y_k, h_k, i = 1, n,j = n +1, p, к = 1, p отличны от нуля, u – скалярное управление, переводящее систему из начального положения в начало координат за минимальное время, |u| <  l,E,p – малые положительные параметры. Введем обозначения

1, n, j = n + 1, p, тогда

-aixt3-biyi+yiu,i =

^i = Yi-^j = z_? i = система примет вид: if = Yi^j = yj^Yi ^:=

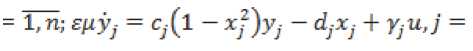
П + l,p; Z =2^=1 ^k^k-

Пусть для системы (6) выполняются условия 1) – 3), 1’) – 3’). Произведем замену переменных

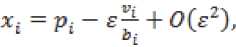
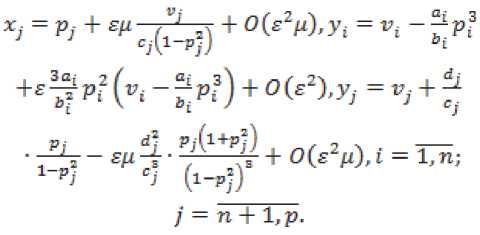
В результате получим систему блочно-треуголь-

ного вида:

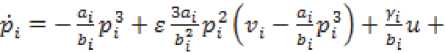
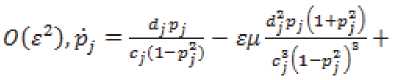
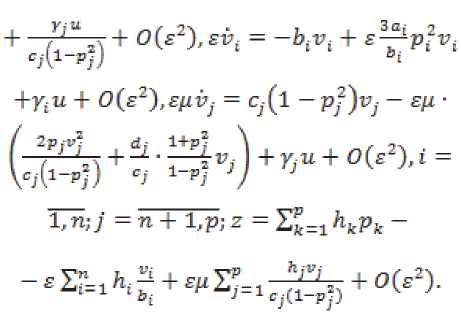
Система блочно-треугольного вида является локально вполне управляемой вблизи начала координат и локально вполне наблюдаемой вблизи начала координат, так как медленная подсистема нулевого приближения, первая быстрая подсистема первого приближения и вторая быстрая подсистема второго приближения локально вполне наблюдаемы вблизи начала координат. Так как блочно-треугольная система получена из системы (6) с помощью обратимой замены переменных, то система (6) локально вполне управляемая и локально вполне наблюдаемая вблизи начала координат.

ЗАКЛЮЧЕНИЕ

В настоящей работе проведено исследование моделей систем, описываемых сингулярно возмущенными системами дифференциальных уравнений и изучены свойства управляемости, наблюдаемости, стабилизируемости. Проведена декомпозиция моделей управляемых и наблюдаемых нелинейных автономных трехтемповых систем. Сформулированы достаточные условия управляемости и наблюдаемости нелинейных трехтемповых систем. Изучены свойства управляемости и наблюдаемости автономной трехтемповой системы нелинейных осцилляторов вблизи начала координат.

Автор выражает глубокую признательность профессору В.А. Соболеву за полезные обсуждения и ценные советы.