Управляемые системы: условия экстремальности, оптимальности и идентификация алгебраической структуры

• I.    Условия экстремальности в управляемых системах и задачах оптимального управления

Рассмотрим управляемую систему x = f (t,x,u) u(t) E U

на произвольном отрезке времени T = [t o ,t i ] и всевозможные процессы этой системы — пары функций (x,u) E AC(T,Rⁿ) • L ^ (T,U ), удовлетворяющие (1) почти всюду на T .

Предполагая функцию f непрерывной и достаточно гладкой, определим функцию Понтряги- на:

H(t,x,p,u) = p • f (t,x,u)

и сопряженную систему p = -Hx(t,x,p,u), q = -Ht(t,x,p,u).

Экстремалью системы (1) назовем любой процесс (x,u), для которого существует решение (p(t),q(t)) = 0 системы (2), обеспечивающее условия максимума функции H по u E U :

^H(t, ^x(t), p^(t), ^u(t)) + q(t) = 0,

^H(t, ^x(t), p^(t), v) ⁺ q^(t) 6 ⁰

t∈T, при      (t, v) E T • U.

В этом случае набор функций y = (x(t), u(t), p(t), q(t)) назовем биэкстремалью системы (1), а пару (p, q) — коэкстремалью. (По поводу этих понятий см. [1-4].)

Ясно, что оптимальное решение любой задачи динамической оптимизации в системе (1) (без поточечных фазовых и смешанных ограничений) следует искать среди биэкстремалей системы, удовлетворяющих дополнительно соответствующим краевым условиям. Но это уже будут биэкстремали задачи (соответственно экстремали и коэкстремали задачи). Отметим, что в подобной ситуации биэкстремали иногда называют каноническими экстремалями [5] и даже просто экстремалями [1, 2]. Компоненту q(t) сопряженной системы (2) при этом часто опускают, хотя в задачах с нефиксированными моментами времени её введение эффективно и почти неизбежно (хотя бы в неявной форме). Из (3) следует стандартное условие максимума функции H по u ∈ U, которым можно ограничиться в задачах управления на фиксированном отрезке T , что и делается далее. В этой ситуации условия экстремальности в системе (1) принимают вид канонической системы:

x = H p , p = -H x                                 (4)

и условия максимума:

u G U * (t,x,p).                                               (5)

Здесь

U*(t,x,p) = {u G U|u G Arg max H(t,x,p,u)} u∈U

— множество предэкстремальных управления (предстратегий). Обозначим через E множество троек функций (x,u,p), удовлетворяющих условиям (4), (5) на отрезке времени T .

Заметим, что при аналитическом исследовании конкретных задач оптимального управления с помощью принципа максимума Понтрягина (ПМП) имеют дело именно с системой (4), (5). Для дальнейшего важно иметь в виду связь системы условий экстремальности с решением уравнения Гамильтона–Якоби–Беллмана методом характеристик [6, 7] и его версиями при использовании неравенств Гамильтона–Якоби [3, 6, 8--10]. А именно, если в системе (1) рассматривается задача терминального управления со свободным правым концом, то есть при условиях

x(t o ) = x o , x(t 1 )      свободно,       J(u) = l(x(t 1 )) ^ min,                 (6)

то имеет место равенство (для простоты считаем, что оптимальное управление существует)

min J (u) = min { l(x(t i )) | (x,u,p) G E ,x(t o ) = x o ,p(t i ) = — l(x(t i )) } , U = L ^ (T,U ).       (7)

Его естественный аналог имеет место и для функции Беллмана семейства задач типа (1), (6) с варьируемой начальной позицией (t o ,x o ). Однако задач оптимального синтеза мы не касаемся.

• II.    Монотонные потенциалы канонической системы и их приложения

Перейдем к предлагаемому обобщению методов, основанных на использовании неравенств (и уравнений) Гамильтона-Якоби. Пусть F — множество функций S(t,x,p) : T х Rn х Rn ^ R непрерывных и гладких по (x,p) при фиксированных t G T и липшицевых по t при фиксированных (x,p) (тогда функции S суперпозиционно абсолютно непрерывны и даже липшицевы вдоль траекторий (x,p) канонической системы (4)). На таких функциях, которые условимся называть потенциалами, определим оператор r[S] = S полной производной по t в силу системы (4), то есть в краткой записи:

r[S ] = S t + S x H p

—

S p H x .

При фиксированной S G F правая часть есть функция (t,x,p,u) и можно определить функцию (или оператор)

r * [S] = maxr[S] = max S ,                                (9)

если множество U компактно.

По аналогии с [8, 9, 11, 12] введем следующие понятия:

S сильно убывает (относительно системы (4) на множестве Ю : = T х Rⁿ х R ⁿ ), если

r*[S](t,x,p) 6 СнаЮ или r[S](t,x,p,u) 6 СнаЮ х U;

S слабо возрастает, если

r * [S](t,x,p) >  СнаЮ.

Заметим, что S — первый интеграл канонической системы, если r[S] = 0; он относится к сильно убывающим потенциалам. К ним относим и решения уравнения r * [S] = 0.

Поясним, что если S сильно убывает, то суперпозиция S (t, x(t), p(t)) монотонно не возрастает вдоль любого решения (x,p) системы (4) с графиком в Q. Предположим, что в системе (1) при любом выборе управления решение существует на T , а в системе (4) множество скоростей компактно и выпукло. Тогда если S слабо возрастает, то для любой точки (t * , x * , p * ) Е Q- существует хотя бы одно правостороннее решение системы (4), начинающееся в этой точке и имеющее график в Q, вдоль которого S(t, x(t), p(t)) не убывает. Введенное сочетание свойств монотонности потенциалов можно заменить на комбинацию «сильно возрастает — слабо убывает» путем замены оператора Г * на r * [S] = min _uGu r[S] и смены знака неравенств на противоположный. Ясно, что эти формальные изменения соответствуют смене знака функции S Е F.

В частном случае — для функций, не зависящих от p , — потенциалы переходят в функции типа Ляпунова управляемой системы (1), если их трактовать достаточно широко, как в канонической теории оптимальности Гамильтона–Якоби [3, 9--12]. При этом неравенства (10), (12) трансформируются в стандартные неравенства Гамильтона–Якоби:

S t + H (t, x, S x )

6 0

> 0

на     Q, на     Q,

где

H (t,x,p) = max H (t,x,p,u) u ∈ U

• — гамильтониан. (В этом контексте отметим, что мы называем систему (4) канонической, а не гамильтоновой, в которую она переходит при замене функции Понтрягина H на H, то есть при выборе управления из (5). Однако это требует нетипичной гладкости гамильтониана.)

Как и в случае стандартных потенциалов (не зависящих от p) сильно монотонные функции позволяют получать внешние оценки множества соединимых точек (множества достижимости) канонической системы и оценки снизу целевого функционала задачи оптимизации, следовательно, с их помощью можно получать достаточные условия оптимальности. Напротив, слабо монотонные потенциалы дают внутренние аппроксимации множества соединимых точек системы (4) и оценки сверху целевого функционала. Таким образом, они приспособлены для получения необходимых условий оптимальности, а также методов улучшения неоптимального управления по схеме работ [9, 11, 13], см. также ниже п. 4.

Ограничимся здесь одним из результатов.

Обозначим через R [ a,b ] множество точек, соединимых решениями системы (4) на отрезке [a,b] С T , то есть

^R [ a,b ] = ^{q ^:= ^(x(a), P^(a); ^x(b), P(^b)) l (x( - )> P0) - решение ⁽⁴⁾ на      ^[a,b]}.

Теорема 1. Пусть X C F — произвольное множество сильно убывающих потенциалов. Тогда имеет место включение

R [ a,b ] C E [ a,b ] (X), где множество E [ _a,b ] (X) состоит из векторов q = (x _a ,p _a ; Х ь ,р ь ), удовлетворяющих системе неравенств

S(Ь,х ь ,р ь ) - S(a,X a ,P a ) 6 0 V S Е X.                              (13)

Вспоминая равенство (7), сформируем следующую конечномерную задачу оптимизации, вспомогательную (терминальную) по отношению к задаче управления (1), (6):

l(x) ^ min; q Е E T (X),

где множество E t (X) соответствует [a,b] = T и учету условия x(t g ) = x g .

Следствие 1. а) min u GU J (u) >  min _qGE T (_S) l(x) =: ^(X);

• б) если для управления и Е U и соответствующей траектории X найдется такое множество X C F сильно убывающих потенциалов, что l(x(t i )) = ^(X), то и — оптимальное управление.

С учетом предваряющих пояснений эти утверждения почти очевидны. Отметим лишь, что при формировании множества E T (X) условия трансверсальности для котраекторий не обязательно считать выполненными (соответствующие примеры имеются в [3]).

Следствие 1 распространяет достаточные условия оптимальности с множеством сильно монотонных функций типа Ляпунова на случай потенциалов и формально охватывает их. Хотя к настоящему моменту времени не накоплен достаточный опыт работы по изложенной схеме, представляется, что альтернативные варианты могут не уступать ей в эффективности. Опишем их кратко.

• 1)    Переход к стандартным потенциалам. Если множество X достаточно богато, то по его функционально независимым наборам из n потенциалов можно построить некоторое множество стандартных сильно монотонных потенциалов (путем ввостановления функции по заданному градиенту) и далее действовать по традиционной схеме. В этом случае оценочное множество (13) и ограничения терминальной задачи (14) будут подмножествами фазового пространства, что более естественно. Например, для управляемых L-систем, обладающих набором из n первых интегралов канонической системы (4), линейных относительно импульса p, этот путь может оказаться особенно эффектным, и не только для анализа ПМП, приведенного в [14].

• 2)    Множество стандратных потенциалов, построенных по варианту 1), можно использовать в модифицированных условиях оптимальности Каратеодори и Кротова [9, 10], рассматривая соответствующий обобщенный лагранжиан задачи (см. [15] и конструкцию K -функций в [16]).

Для иллюстрации рассмотрим элементарный

Пример 1. задачи оптимального управления в одномерной L-системе:

x = (x — 1)u, u E [0,1], x(0) = 0, J = x ³ (1).

Условие ПМП таковы: H = p(x — 1)u, p = —pu, p(1) = —3x2(1), p(x — 1)u ^ max; u E [0,1]                   (15)

(то есть H u (x,p)u ^ max; u E [0,1]).

Во-первых, заметим, что H u = 0, то есть S 1 (x,p) = p(x — 1) — первый потенциал, диктуемый теорией L-систем. Он является частным решением неравенства сильной монотонности (11):

[(x — 1)S x — pS p ]u 6 0.

Но оно имеет, как легко убедиться, с учетом краевых условий еще два решения: S 2 (x) = x и S ³ (p) = — p.

Далее, естественное использование S ¹ для упрощения ПМП, описанное в [14], предписывает заменить условие максимума из (15) на следующее: cu ^ max; u E [0,1], то есть u E sign c, где константа с зависит от искомой траектории (x,p) через равенство S ¹ = с. Возникает необходимость перебора вариантов значений c при выполнении условий

• — 3x ² (1)(x(1) — 1) = с, x(1) 6 0 ( это дает     S 2 ).

Отсюда с >  0 и возможны два случая:

• (а)    с = 0, тогда x(1) = 0, откуда р * = 0, x * = 0, u * = 0 — особая биэкстремаль задачи;

• (б)    с > 0, тогда u = 1, x(t) = 1 — e t — неособая экстремаль.

Поскольку задача невыпуклая, то это все, что дает ПМП. Так как оптимальное управление в задаче существует, то очевидно, что u — решение задачи. Однако интересно, что дают формальные методы без привлечения теоремы существования.

Покажем, что особое управление u * = 0 не оптимально (заметим, что все локальные условия оптимальности оказываются не эффективными в силу глубокого вырождения этой экстремали). Воспользуемся конструкцией улучшения управления из [9, 11]: так как S ² слабо (и сильно) убывает, то для любой траектории x( - )

x(1) — J(u * ) = x(1) 6 0 и, следовательно, x ³ (1) — J(u * ) 6 0, что и требовалось.

Установим теперь оптимальность u = 1, пользуясь достаточными условиями следствия 1 с учетом замечания 1). Потенциал S ¹ порождает (из равенства S _x = р = c/(x — 1)) функцию

S (t,x) = ln(1 — x)£(t), где ((t) > 0 — произвольная гладкая функция. Для нее (см. (9))

с

r * [S ] = max S = ((4+ 1 = 0, u G U       ((t)

если выбрать ((t) = ((0)e ^{- t} , ((0) > 0. При этой ( S (t,x) удволетворяет уравнению Гамильтона-Якоби и, следовательно, сильно убывает. Положив теперь в следствии 1 X = { S } — одноэлементное множество, убеждаемся, что xq1) является решением терминальной задачи (14). Это и означает оптимальность управления u.

• III.    Системы с алгебраической структурой

Определение 1 [14, 17]. Система с управлением u l (в (1) f (t,x,u) = +(x)u)

n xk = X +k (x)ul(t),     k =i,n,                               (16)

l =1

называется L-системой, если для функций +k(x) выполнены условия det||+k (x)||=0,                                                  (17)

где обозначено

[X i ,X j ] = X C j X k , C k = const, i,j, k = 1,n, k =1

n k∂

^i dxk, l = 1,n, k=1

[X i ,X j ] — коммутатор операторов (19):

n

XX ] = X { X i + (x)

k =1

- X ^(x)} ..

Пример 2. Уравнение Ньютона ms = u(t) — es ² , определяющее одномерное движение управляемой точки при наличии сопротивления пропорционального квадрату скорости, погружается в L-систему

(x \    / 1 2x x2 \ / u1 \ y   =   0 2 2x u2                               (21)

z У у 0 0 ey У \ и3 У при следующей специализации переменных:

x = ms, y = — 2se/m, u ¹ = u(t), u ² = 0, u ³ = — в/(т) 2 .

Для соответствующих системе (21) операторов (19)

X 1 = I-, X 2 = 2x^X +2 ^, X 3 = x^{2 X} + 2x^ + e y               (22)

∂x         ∂x ∂y         ∂x ∂y ∂z выполняется условие (18) с постоянными C12 = 2, С2з = 1, С3з = 2 (здесь и далее приводятся только ненулевые структурные постоянные Cikj , удовлетворяющие условию i < j). Третье уравнение в (21) добавлено, чтобы матрица в (21) стала квадратной и для нее были бы справедливы условия (17), (18).

Условия (17), (18) удостоверяют, что операторы (19) могут быть приняты за базис алгебры Ли, которой соответствует просто транзитивная n-параметрическая группа:

x k = g k (x 0 , ..., x o , v 1 , ..., v n ), k = 1,n,

определенным образом построенная по базисным операторам (19) [14, 20]. Любая пара { u(t), T } , где u(t) — конкретное подставленное в (15) управление, определяет преобразование пространства R n (x): сдвиг вдоль решений x(t) начальных точек x g = x(0) в конечные x(T ). Показывается [19], что для каждой пары { u(t), T } найдется набор параметров v ¹ . ..., v n , определяющий при помощи (23) соответствующее паре { u(t), T } преобразование сдвига вдоль решений системы. Показывается также [17, 19], что по функциям v k (x), задающим L-систему (15), строится система уравнений для нахождения генераторов n-параметрической группы симметрий системы (15). Опуская вычисления, приведем уравнения группы симметрий для системы (21):

__ x + T i ( e y — xz )

x =    1—T1Z   , y = y + T2 - 2ln(1 - Tiz),

~ _ z ( e ^T2 — T 1 T 2 + T 3 )

z           1 — T 1 z      .

Каждому набору параметров T i , T 2 . T 3 соответствует замена переменных в (21), не меняющая вид правых частей, и любое решение u(t), x(t). y(t). z(t) системы (21) группа переводит в решение u(t), x(t), y(t), z(t) (функции u(t), x(t), y(t), z(t) подставляются в правую часть уравнений группы).

• IV.    Классы эквивалентности для L-систем

Для L-систем справедлив следующий результат, который приведем без доказательства. Теорема 2 [14, 20]. Две L -системы: (15) и n zk = X SPk ИМ k = 1.n.

l =1

удовлетворяют условиям (17)--(19) с одними и теми же постоянными C _i ^k _j в (18) тогда и только тогда, когда они связаны диффеоморфизмом z = z(x).

Если системы (15), (24), связанные диффеоморфизмом x О z, считать эквивалентными, то каждому классу эквивалентности соответствуют постоянные C _i ^k _j :

' ^x k = E / =i V k ^(xW

^ {C } .

<       | x О z zk = Pn=i Vk(z)u1

Соответствие — взаимно однозначно: по структурным постоянным C _i ^k _j вычисляется некотoрый базис X i . .... X n алгебры Ли [14, 20], по операторам X j определяется представитель (15) класса эквивалентности (25) с возможностью диффеоморфизмом перейти к другому представителю. Набор C _i ^k _j являет собой пример инвариантной математической модели динамической системы. По этому набору можно исследовать те свойства системы, которые сохраняются при заменах переменных: управляемость, структура оптимального управления и т.д. Aлгебраическая структура, определяемая C _i ^k _j , позволяет строить в соответствующем классе эквивалентности (25) представители специального вида: линейного, билинейного, двухуровневого, блочного и т.д.

Пример 3. Линейная стационарная (автономная) управляемая система (A = || а ^ | , B = || b k || — числовые матрицы)

x = Ax + Bu, x Е Rⁿ.   u E R.

погружается в класс L -систем:

x0 VP 0 W 1 A

5c ) у Ax E J у Bu )

(E — единичная матрица) добавлением к (26) верхнего уравнения. Проверка для (27) условия (18) приводит к постоянным в (18): C0k = —ak, l.k = 1.n (нумерация столбцов в (27) и соответствующих операторов в (19) начинается с номера 0). Постоянные ClQk = —alk, l.k = 1.n, определяют инвариантную модель { Cikj } соответствующую классу эквивалентности (25), которому принадлежит система (27), то есть в соответствии с теоремой 2 любая, в том числе и нелинейная, неособенная замена переменных в (27) приведет к L-системе (24) с таким же, как у (27), набором постоянных Cl№ = —ak, l,k = 1,n, в (18). Теорема 2 дает ответ и на вопрос: возможно ли конкретную нелинейную систему заменой переменных привести к линейному виду? Возможна тогда и только тогда, когда система является системой с постоянными C0k = -ak, l,k = 1,n.

У следующих трех механических систем соответствующие L-системы принадлежат одному и тому же классу эквивалентности (25), то есть постоянные C _i ^k _j в (3) у систем совпадают.

Пример 4. Одномерному линейному осциллятору x + x = 0

соответствует L-система (1) (x ² = x)

с постоянными C _i ^k _j в (18):

x ¹

de ²

x ³

1 x ³ - x ²

1 0 u

C ₁₂ = 1,

C 13 = ^—1.

Пример 5. Тело с неподвижной точкой, с осью динамической симметрии — первой главной осью инерции (B = C ), с управляющим моментом M , направленным по третьей главной оси. Динамические уравнения Эйлера имеют вид

Р = 0, q = BBA Рг, r = abb pq + B m.

Переход на поверхность p = const, выбор масштабов для времени t ^ at и управления М ^ и = вМ приводят к уравнениям q = r, r = —q + и, которым соответствуют такие же, как в примере 3: L-система (29) и постоянные Cikj (30).

Пример 6. Точка движется в плоскости ( x 2 , x 3 ) под действием силы F , перпендикулярной скорости V . Aнализ показывает, что при таком движении скорость V не меняется по величине. Введение переменной x 1 — угла между осью x 2 и направлением скорости V — и выбор масштабов для x 2 , x 3 , F приводит к уравнениям

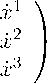
u cos x1

sin x 1

0 cos x 1

0 sin x 1

— sin x 1 cos x 1

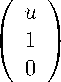
Проверка условий (17), (18) показывает, что система (31) есть L -система с такими же, как в примерах 3, 4, постоянными (30).

Вследствие теоремы 2 заменой переменных можно добиться совпадения матриц Ц^ (x) ^ в правых частях систем (29) и (31), но то, что у систем по-разному специализированы управления u ⁱ , приводит к существенным различиям их свойств с точки зрения возможностей управления. Дополнительное требование — одинаковое расположение в пространстве R ⁿ у двух систем множеств U допустимых управлений — приводит к понятию более сильной зквивалентности, чем было определено ранее. Этот аспект в данной работе не затрагивается.

• V.    Идентификация алгебраической структуры

Инвариантная модель { C _i ^k _j } есть результат завершения следующего процесса: имеется реальная система с входными переменными — управлениями u = (и ¹ , ..., u n ) и выходными переменными x = (x ¹ , ..., x n ), системе сопоставляется математическая модель (15), специальные свойства (17)--(19) которой приводят к взаимно однозначному соответствию (25). L-система (15) в приведенном процессе играет промежуточную вспомогательную роль «производителя» структурных постоянных C _i ^k _j , и естественно поставить вопрос о нахождении чисел C _i ^k _j , экспериментируя с исходной реальной системой. К ответу на вопрос приводит следующая последовательность воздействий на систему. Для нахождения постоянных C _α ^k _β с фиксированными нижними индексами а и в в а-й канал подается единичное воздействие: и¹ = 5¹ _а . За малое время т система из начального состояния x 0 переходит в состояние x 1 . Затем единичное воздействие подается только в в-й канал: и¹ = 8 в , за то же время т происходит переход x i ^ x 2 - В течение того же времени т подается вход и¹ = —5¹_а , и затем то же время т — вход и¹ = —8 в . Состояние системы возвращается в окрестность начального:

x0 → x1 → x2 → x3 → x4 ≈ x0, но с рассогласованием. На последнем шаге подбирается такой постоянный вход U, чтобы система за время т = т2 осуществила переход xo ^ x4 за один шаг. Структурные постоянные равны

C ie = U i .                                         (32)

Описанная процедура повторяется для всех пар индексов α, β. К результату (32) приводят прямые вычисления, основанные на системе (15). Представим начальный и конечный этапы:

x k = x k +^тy a ^(x o ) + 2 ^{т 2} P n =i <лы ^dsB x^ +^{о(т 2 )},

тк _ к ,  2 Pn   ( l д^в ml d^aa )       i 2\ _ x4 = xo + т 2=1=1 I r a dxl - г в dxl /      + 0(т ) = x=x0

=xk+т 2 Pn=i Cae yk (xo)+о(т 2), использовано свойство (18) L-системы. С другой стороны:

n xk = xk + т X yk(xo)ul + о(т), l=1

что с учетом формулы (33), условия (17) и т = т ² с точностью до о(т 2 ) определяет результат (32).

Замечание 1. Формула (32) асимптотически — при т ^ 0 — точна.

Замечание 2. Приведенная процедура носит инвариантный характер: в каких бы переменных x не измерялся выход, результат (32) один и тот же.

Замечание 3. Результат (32) не зависит от начального состояния x 0 , в окрестности которого проводится процедура.

Замечание 4. Пусть система имеет вид (15), выполняется условие (17): det || y k (x) ^ = 0, но не выполняется условие (18), то есть (15) не L-система. Определим постоянные C _α ⁱ _β так, чтобы в равенстве (33) совпали коэффициенты при τ ² , а именно:

Ci ав =

n iX k,l=1

^{ϕ l}α ^∂∂^ϕx ^kβl

-

_{ϕ l} ∂ϕ ^kα ^{ϕ β} ∂x ^l

ψ kⁱ

где || ^ ^k (x) П = ll ^ k (x) H 1 . Описанная процедура, примененная не к L-системе (15), приводит к постоянным, совпадающим с (34). Проверка показывает, что постоянные C _α ⁱ _β , определенные формулой (34), удовлетворяют условиям, которым должны удовлетворять структурные постоянные алгебры Ли [20]: антисимметрия по нижним индексам и тождество Якоби. Эта алгебра инвариантно аппроксимирует исходную систему в окрестности выбранного начального положения x 0 .

Работа выполнена при финансовой поддержке СО РАН (интеграционный проект СО РАН–УрО РАН № 85), РФФИ (гранты 11-01-00672-а, 10-01-00228) и АВЦП Развитие научного потенциала высшей школы 2009–2010 гг. (проект 2.1. 1/3604).

• VI.    Заключение

С целью расширения сферы применимости методов теории управления, связанных с решениями неравенств и уравнения Гамильтона–Якоби, введен новый класс функций типа Ляпунова, зависящих от канонических переменных дифференциальной системы условий экстремальности, и обладающих свойствами сильной и слабой монотонности относительно решений этой системы. Предлагаются способы использования этого класса функций для решения позиционных и оптимизационных задач управления. Обсуждена также возможность выявления структурных постоянных алгебры Ли, моделирующей управляемый процесс.