Упрощенный алгоритм построения вероятностной модели оценки степени рисков инновационных проектов

ВЕЛИКОИВАНЕНКО В.И.

ГУСАКОВ Н.В.

ПАНТЕНКОВ Д.Г.

СОКОЛОВ В.М.

В статье предлагается новый упрощенный метод построения вероятностной модели оценки степени риска инновационного проекта. Метод базируется на теории нечетких множеств, методах математического и имитационного моделирования [1-8].

Существующие научно-методические подходы [9-16] имеют ряд следующих недо-cтатков:

• •    отсутствует обобщенная модель оценки степени рисков, инвариантная ко входным параметрам;

• •    представленные результаты математического моделирования в части оценки степени рисков требуют более наглядной графической интерпретации;

• •    известные модели определения степени рисков ориентированы на их оценку лишь по одному параметру (частный случай), что приводит к невозможности сопоставления сравнительной оценки степени рисков по двум и более параметрам одновременно.

Постановка задачи

Требуется предложить алгоритм построения вероятностной модели оценки степени рисков инновационных проектов, позволяющий в первом (грубом) приближении дать экспресс-оценку рентабельности и реализуемости инновационного проекта по одному, двум и, в самом общем случае, N выбранным критериям. На основе предложенного математического аппарата провести компьютерное моделирование, проанализировать полученные результаты, сделать выводы.

Упрощенный алгоритм построения вероятностной модели оценки степени рисков инновационных проектов по одному критерию

Исходные данные. В качестве оценки

степени риска инновационного проекта целесообразно взять параметр рентабельности C _РЕНТ [12–15]. Входными параметрами в данном случае являются полученные методом статистического анализа (выборки) усредненная величина Z _ПОР (норма прибыли от внедрения инновационного проекта) и предполагаемое значение рентабельности проекта C _РЕНТ. Пусть для данного параметра, при условии выполнения неравенства C _РЕНТ<  Z _ПОР, внедрение инновационного проекта считается нецелесообразным.

Предположим, что множества возможных значений параметра C _РЕНТ и критерия оценки (порога) Z _ПОР зада ны в виде треугольн ых н ечетких множеств С _РЕНТ = [ С _min, C ₀, C _max], Z _ПОР = = [ Z _min, Z ₀, Z _max]. Требуется, исполь зуя з а дан ные параметры нечетких множеств С _РЕНТ, Z _ПОР, оценить риск внедрения инновационного проекта.

Решение задачи. Функции принадлежности треугольных чисел имеют вид соответственно [1-3]

C 0 — C min

x

C min

^C- - C 0

> C < x <  С 0 ;

min

Ц C ⁽ x ) = <

C 0 - C max

x +

C _____ max

C max — C 0

. C 0 <  x <  С , ,„;⁽¹⁾

⁰, ( X <  ^С min ) V ( X >  С max )-

Z 0 — Z min

¹--- x +

Z min

7   7

Z   Z ₀

, Z min <  x <  Z 0

min

Ц Z ⁽ x ) = <

^Z 0 — ^Z max

x +

Z max

^Z max — ^Z 0

, Z 0 <  x <  Z max ; ⁽²⁾

⁰, ( X <  Z min ) V ( X >  Z max )

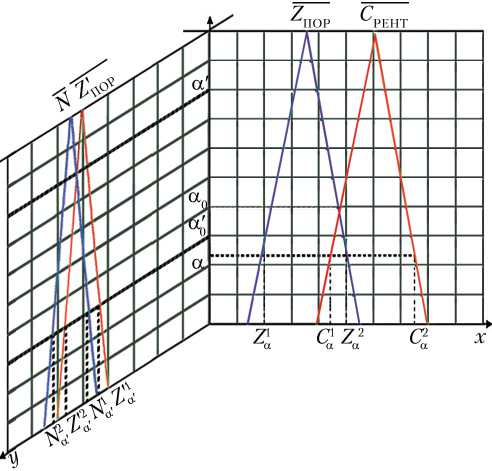
Если построить графики функций µ _C ( x ), µ _Z ( x ) в одной системе координат, то в зависимости от текущих значений [ Z a , Z ^ ] и [ С а , CO.] возможны различные варианты расположения графиков заданных функций относительно друг друга. Общая схема рассуждений, используемых в данном методе, не зави си т о т расположения треугольных чисел С _РЕНТ, Z _ПОР, следовательно, будем рассматривать более подробно один из вариантов, представленный на рис. 1.

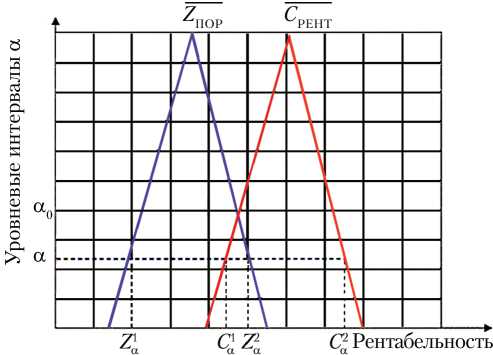
Рис. 1. Зависимость величин С _РЕНТ и Z от рентабельности в α –уровневых интервалах для одного выбранного критерия

Рассмотри м α - у ровн евые множества нечетких чисел С _РЕНТ, Z _ПОР. Будем полагать, что условие C _РЕНТ<  Z _ПОР в α -уровневых множествах порождает риск неэффективности внедрения инновационного проекта.

При α ≥ α ₀ (рис. 1) соответствующие α -уровневые интервалы не пересекаются и, следовательно, рисковая зона отсутствует, а при α <  α ₀ существует опасность того, что значения C _РЕНТ, входящие в пересечение интервалов [ Z a , Z ^ ] и [ С а , C^L могут быть меньше, чем значения Z ПОР , т. е. интервал [ C ^ , Z ^ 2 ] является зоной риска.

Перенеся для выбранного α соответствующие интервалы на ( C , Z )-плоскость, получим график, представленный на рис. 2.

На рис. 2 заштрихованная область показывает зону риска, а весь прямоугольник — область возможных реализаций значений выбранного параметра.

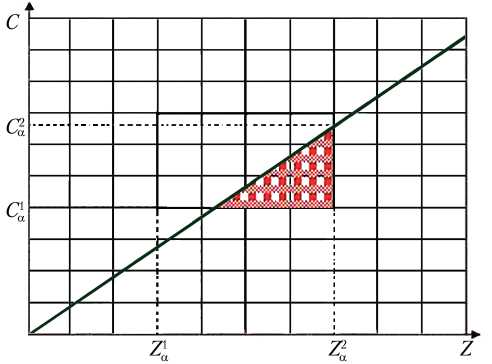
Рис. 2. Результат перехода от α –уровневых интервалов в (C, Z)-плоскость для одного выбранного критерия

Для выбранного α -уровня вероятность попадания точки с текущими координатами ( C , Z ) в заштрихованную область представляет собой вероятность недостаточного уровня рентабельности для данной пары значений параметров.

Обозначим эту вероятность через P ( α) . Тогда P ( α) определяется согласно выражению (график функции представлен на рис. 3) [3]

5 1 ( a )

P ^{( a )} 5 ₂( a ) ^, (3)

где S ₁( α) — площадь заштрихованной области;

S ₂( α) — площадь прямоугольной области.

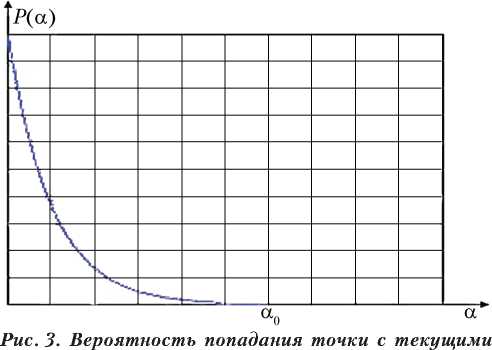
координатами (C, Z) в заштрихованную область для выбранного α -уровня

Отметим некоторые важные свойства функции P ( α) :

1. Если выразить площади S ₁( α) , S ₂( α) через α в явном виде, то после элементарных преобразований получим выражение вида:

P ( а ) =

. 2 ML

Aα + B а - 1

А 2

- , 0 <  а <  а ₀;

0, ( а < 0) v ( а >  а ₀),

где A = Z _ПОР M = Z – Z

– С _ОКУП – Z _max + C _min; B = Z _max – C _min;

min max

; L = C min – C max .

• 2.    0 ≤ P ( α) ≤ 1.

• 3.    P ( α) — убывающая на отрезке [0, α₀ ] функция.

• 4.    max P ( ^a ) = P (0) = ——-;

• 5.    0 ≤ P ( α ) d α ≤ 1.

B ²

0< a < a0             2 ML min P(a) = P(a0) = 0.

0< a <  a o

α ₀

После того, как определены вероятности для всех 0 ≤ α ≤ α ₀, целесообразно оценить риск недостаточного уровня рентабельности инновационного проекта.

В предложенном методе в качестве оценки риска берется значение вероятности P ( α) в интересующей точке. Таким образом, для каждого отдельного значения α имеется свой риск. Однако риск для отдельного значения α не может характеризовать величину недостатка рентабельности в целом, так как P ( α) имеет локальный характер. Поэтому здесь уместно ввести величину максимального риска рентабельности, т. е.

B ²

R = max P ( α ) =      .     (4)

^max 0< α <1         2 ML

Максимальный риск не зависит от значений α , а зависит исключительно от значений параметров C _min, C _max, Z _min, Z _max.

Добавим, что предложенный метод явля- ется весьма универсальным и инвариантным к значениям параметров Cmin, Cmax, Zmin, Zmax: вместо выбранного порогового значения недостаточного уровня рентабельности CРЕНТ можно выбрать другой подходящий критерий, при этом сам научно-методический аппарат останется прежним.

В общем случае с помощью предложенного метода ищется глобальный риск (по нескольким критериям одновременно), а затем используется операция свертки, позволяющая его оценить количественно. При этом важно отметить, что критерии независимы, т. е. с позиций теории вероятности, по сути, идет речь об объединении событий, при ко-

тором имеет место логическое произведение вероятностей.

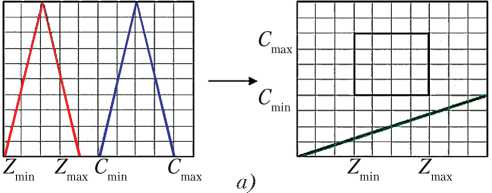
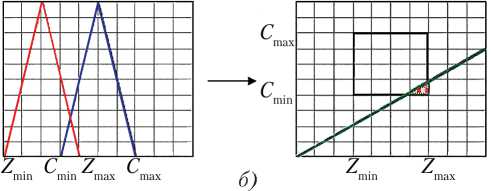
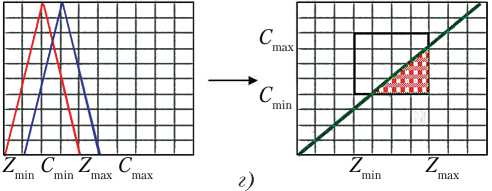
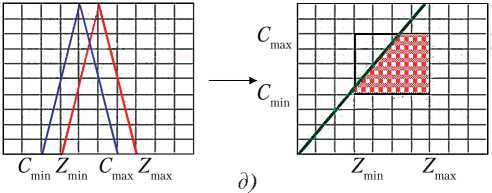
На рис. 4, а–ж представлены количественные оценки степени риска рентабельности ин-

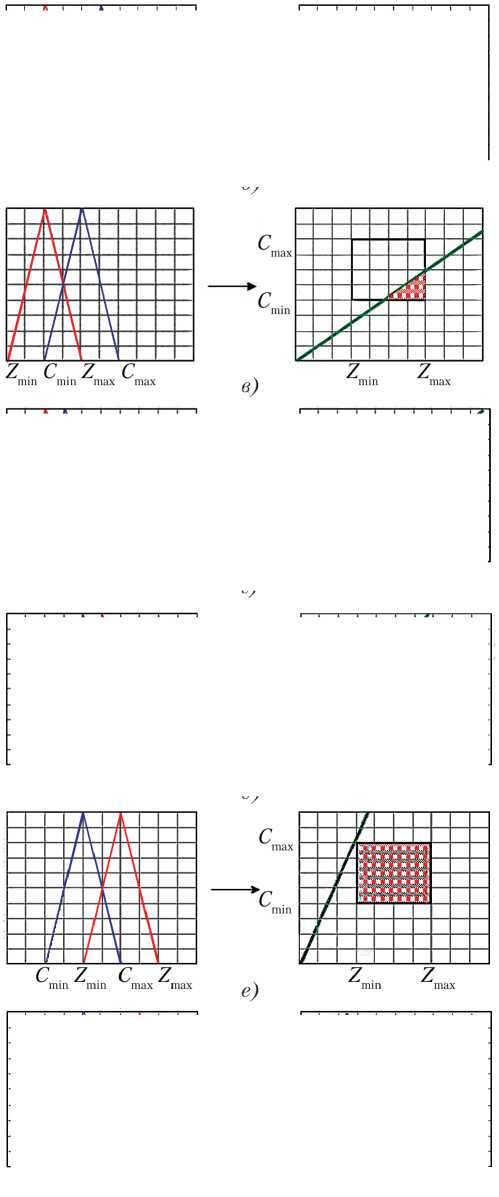
новационного проекта, полученные путем моделирования согласно предложенному методу для различных соотношений параметров C _min, max , min , max .

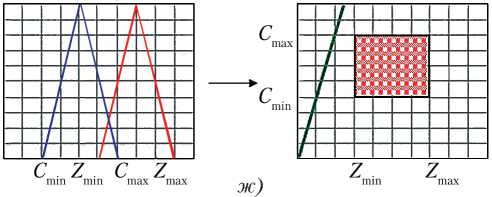
Рис. 4. Этапы перехода от α –уровневых интервалов в ( C, Z ) плоскость для одного выбранного критерия (вариант): а — первый; б — второй; в — третий; г — четвертый; д — пятый; е — шестой; ж — седьмой

В том случае, когда имеет место неравенство Z _max<  C _min (рис. 4, а ), риски являются минимальными. При этом кривая на графике в системе координат ( C , Z ) не пересекает прямоугольник. Далее, по мере движения вправо по оси абсцисс красного графика (увеличение значения Z ) угол наклона кривой в системе координат ( C , Z ) возрастает и отсекает от прямоугольника все большую площадь, что демонстрирует возрастание рисков (рис. 4, б–ж ).

Упрощенный алгоритм построения вероятностной модели оценки степени рисков инновационных проектов по двум критериям одновременно

Распространим предложенный метод оценки рисков разработки инновационного проек-

та для случая оценки степени рисков по двум параметрам (критериям) одновременно. В

этом случае в качестве критериев оценки сте-

пени риска инновационного проекта возьмем параметры рентабельности C _РЕНТ и уровня новизны N инновационного проекта, под которой понимается, например, степень улучшения существующих образцов техники, способствующих получению большего эффекта (большей производительности). Входными параметрами

в данном случае являются полученные методом

статистического анализа величины Z _ПОР (норма прибыли от внедрения инновационного проек-

та), Z _П ′ _ОР (экономический эффект от использования более производительной техники) и предполагаемые значения рентабельности C _РЕНТ и уровня новизны инновационного проекта N .

Исходные данные. Пусть для двух параметров C _РЕНТ, N при условии, что ( C _РЕНТ<  Z _ПОР) ∀ ( N <  Z _П ′ _ОР), внедрение инновационного проекта считается нецелесообразным.

Предположим, что множества возможных

значений параметров C _РЕНТ, N и критерии оцен ки (пороги) Z _ПОР, Z _П ′ _ОР за даны в виде треуголь

-

-

ных нечетких множеств С _РЕНТ = [ С _min, C ₀, C _max];

[ Z min , Z 0 , Z max ]; N = [ N min , N 0 , N max ]; Z _П ′ _ОР = [ _m ′ _in, ₀ ′ , _m ′ _ax]. Требуется, испол ьзуя за дан ны е пар аметры нечетких множеств С _РЕНТ, Z _ПОР,

ПОР

N , Z _П ′ _ОР, оценить риск внедрения инновацион-

ного проекта по двум параметрам одновременно.

Решение задачи. Функции принадлежности треугольных чисел имеют вид [3]

C 0 — C

x +

C min

C _ C ’ C min   x  ^С 0 ’

^Z 0 — ^Z min

Ц Z ⁽ x ) = <

Z 0 — Z max

Ц C ⁽ x ) = <

C 0 — C max

x +

C max

C max — C 0 ,

C 0 <  X <  ^С max ’ (⁵)

⁰, ( X <  ^С min ) ^V ( X >  ^С max )-

Z x +---Sin

7 -7

Z   Z ₀

x +

min

Z m.,

Z max — Z 0

>^Z min <  X <  ^Z 0 ;

. Z . <  x <  Z -;⁽⁶⁾

0, ( X <  Z mm ) V ( X >  Z m _ax).

^N 0 — N n

H N ⁽ У ) = '

min

y

+

^N 0 — ^N max

y

+

N min

^N min — ^N 0 ’

N max

^N max — ^N 0 ’

^N min <  У <  ^N 0

^N 0 <  У <  ^N max ; (7)

0, ( У <  ^N min ) V ( y >  ^N max ).

Z ‘ - Z ' 0 min

Ц Z ⁽ y ) = <

y

Z ′

। min

Z ‘ - Z ’  ^y

0 max

+

Z'. - Z‘ min 0

Z ′ max

, Z ‘. <  y <  Z ‘ ; , min               0’

Z'  - Z‘ , max 0

Z ‘ <  y < Z' ; ⁽⁸⁾ 0            max⁷

0, ( y < Z' . ) V ( y >  Z' ). min            max

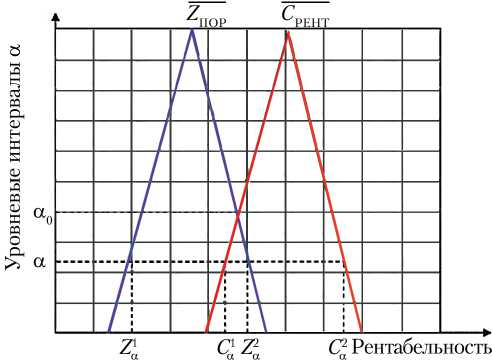
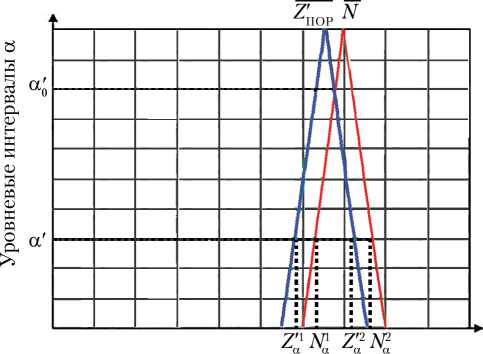
На рис. 5, а показан график функций µ _C ( x ), µ _Z ( x ), а на рис. 5, б — функций µ _N ( y ), µ _{Z ′} ( y ). На рис. 6 представлены на одном графике функции µ _C ( x ), µ _Z ( x ), µ _N ( y ), µ _{Z ′} ( y ) в трехмерной системе координат.

Рассмотрим α-уровневые множества нечетких чисел С , Z , N , Z′ . Будем полагать, РЕНТ ПОР      ПОР что условие (CРЕНТ < ZПОР) ∀ (N < ZП′ ОР) в α-уровневых множествах порождает риск неэффективности разработки и внедрения инновационного проекта.

При условиях α ≥ α ₀, α′ ≥ α′ ₀ соответствующие α -уровневые интервалы не пересекаются и, следовательно, зона риска отсутствует.

В случае, если α <  α ₀, α′ <  α′ ₀ , существует опасность того, что значения C _РЕНТ, N , входящие в пересечение интервалов [ Z a , Z 2 ] n [ С1, C ^ j, [ Z a , Z 0, 2 ] n [ N,, N _a 2 ], могут быть меньше, чем значения Z ПОР (интервал [ C a , Z ^ ] является зоной риска) и Z n _О Р (интервал [ № ‘ , Z ^] является также зоной риска).

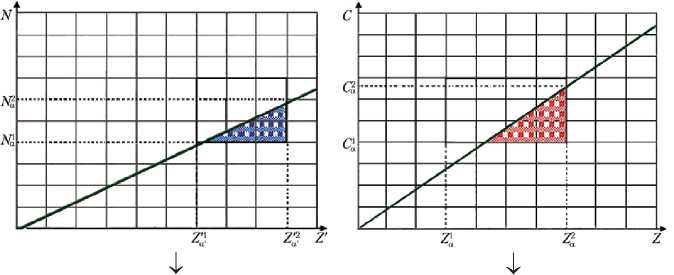
Перенеся для выбранных α , α′ соответствующие интервалы на ( C, Z )-плоскость и ( N, Z ′ )-плоскость, получим следующую графическую интерпретацию зоны риска (рис. 7).

На рис. 7 сверху заштрихованная область показывает зону риска рентабельности инновационного проекта; на рис. 7 снизу — зону риска уровня новизны (недостаточной или, наоборот, слишком высокой), а прямоугольники в целом ограничивают области возможных значений выбранных параметров.

а)

Окупаемость

б)

Рис. 5. Зависимость величин С _РЕНТ , Z _ПОР и N , Z П ′ ОР в α –уровневых интервалах для двух выбранных критериев в двумерной плоскости: а — от рентабельности; б — от окупаемости

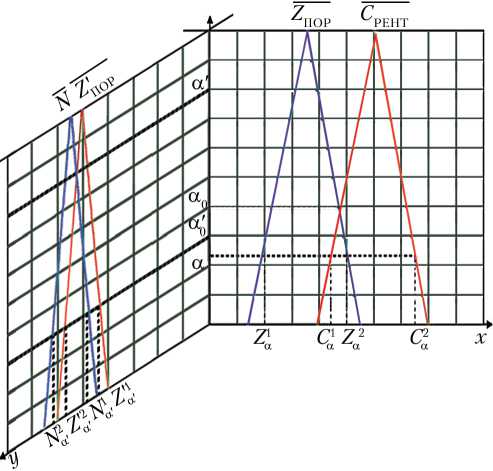
Рис. 6. З ав и сим ость величин С _РЕНТ , Z _ПОР от рентабельности и N , Z _П ′ _ОР от окупаемости в α -уровневых интервалах для двух выбранных критериев в трехмерной плоскости

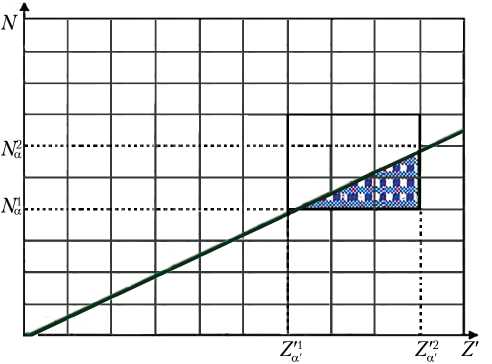
Рис. 7. Переход от α –уровневых интервалов в (C, Z)-плоскость, (N, Z ′ )-плоскость для двух выбранных критериев (вариант)

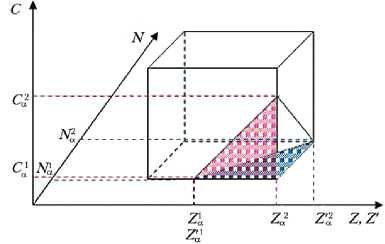
На рис. 8 представлена в трехмерном пространстве зависимость C ( Z, Z ′ ) и N ( Z, Z ′ ).

Для выбранных значений α , α′ -уровней вероятность попадания точек ( C, Z ) и ( N, Z ′ ) в заштрихованные области соответствующих прямоугольников представляет собой вероятность недостаточного уровня рентабельности и уровня новизны для данной пары значений параметров.

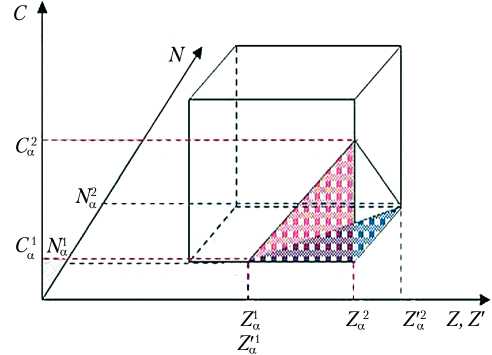
Рис. 8. Результат перехода от α –уровневых интервалов в (C, Z)-плоскость, (N, Z ′ )-плоскость для двух выбранных критериев (вариант)

Обозначим эту вероятность через P ( α , α′ ). Тогда P ( α , α′ ) определяется согласно следующему выражению [10]

⁵ 1 ( a) ⁵ 1 ( a‘)

P ( a , a’ ) = ——-^.    -

5 2 ( a) ⁵ 2 ^{( a})

V ( 0 1 , C 2 , n , N) 0,5 V 2

где S ₁( α ) — площадь заштрихованной области в ( C, Z ) координатах; S ₂( α ) — площадь прямоугольной области в ( C, Z ) координатах; S ₁( α′ ) — площадь заштрихованной области в ( N, Z ′ ) координатах; S ₂( α′ ) — площадь прямоугольной области в ( N, Z ′ ) координатах; V ₁( α , α′ ) — объем фигуры, которой принадлежат обе заштрихованные области; V ₂ — объем куба.

Следовательно, максимальный риск количественно оценивается аналитическим выражением вида [1, 3, 10]

B 2     ( B ' )²

R = max P ( a , a’ ) = __ , _T ^. „,., _T, , (10) ^max o< a <1     ,      2 ML 2 M'L' ’ ^{v 7}

0< a' <1

где B ′ = Z ′ – N ; M ′ = Z ′ – Z ′ max min         min max

; L ′ = N _min – N _max.

Максимальная степень риска не зависит от значениями параметров Cmin, Cmax, Zmin, Zmax, Nmin,

N , Z ′ , Z ′   .

max min max

Численное моделирование

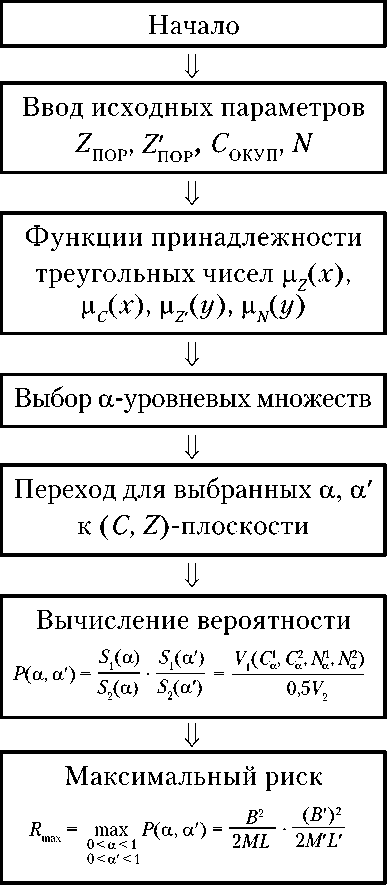
Результаты численного моделирования c использованием формул (1–8) представлены на рис. 9. Полный алгоритм определения оценки рисков инновационного проекта по двум параметрам представлен на рис. 10.

Полученные на рис. 9 зависимости являются результатом численного моделирования. Его характеристики отражают зависимость риска от отношений Z _max/ С _max, Z _m ′ _ax/ N _max при различных фиксированных отношениях Z / C , Z ′ / N . min min min min С увеличением отношений Z / C , Z ′ / N min min min min скорость нарастания функции увеличивается и, как следствие, риски также возрастают.

В настоящее время данный метод проходит программную реализацию, и в ближайшее время появится программное обеспечение, позволяющее в предельно сжатые сроки в наглядном виде количественно оценить риски от внедрения инновационного проекта по одному, двум, трем и более параметрам одновременно.

значений α , α′ , а определяется исключительно

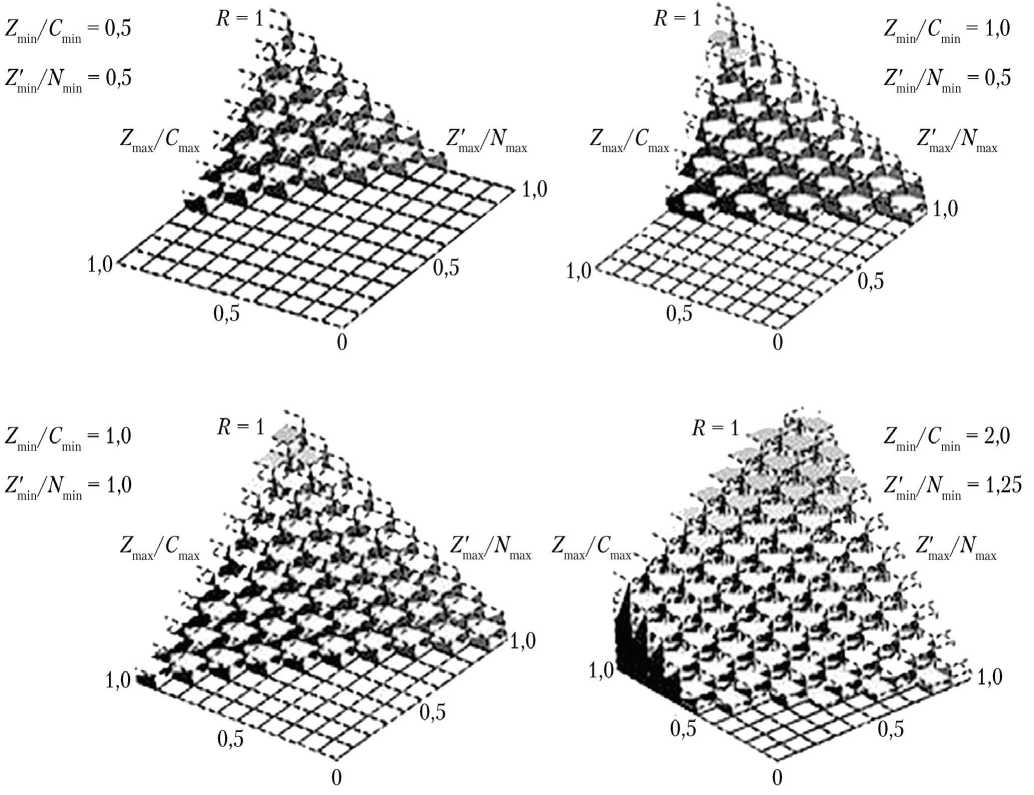
Рис. 9. Результаты численного моделирования оценки степени рисков окупаемости и рентабельности

P ( α′)                         P ( α)

Z _ПОР, Z _П ′ _ОР , С _ОКУП, N

У

α, α′

P ( α, α′)

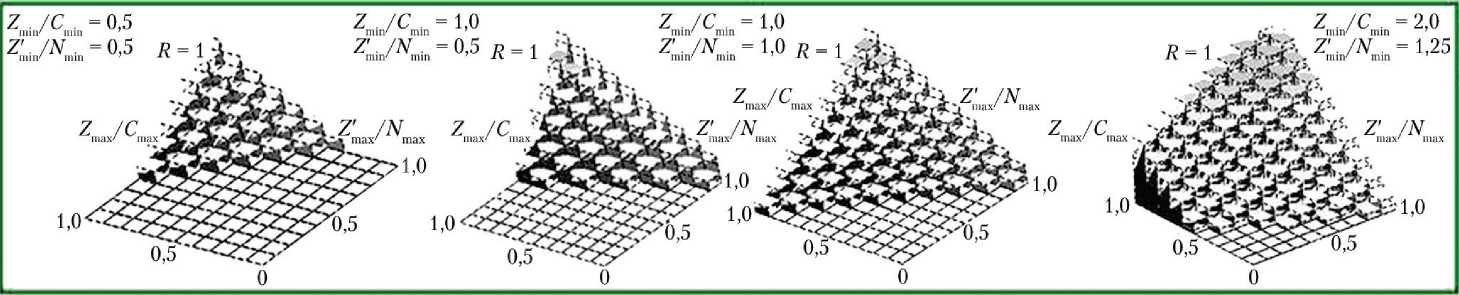
Рис. 10. Алгоритм оценки степени риска по двум параметрам

В самом общем случае аналитические зависимости (9) и (10) имеют вид

P( a , a^f , a" ,...

a n ) =

5 ( a)

⁵ 2 ( a)

⁵ 1 ⁽O _x

5 ( a')

5 i ( a") 5 i ( a n ) 5 ₂( a") ■- 5 ₂( a n ) ‘

Предположим, что порогово е мн ожество задано нечетким множеством вида Z _ПОР = [–1; 0; +1], а апр иорная рентабельность проекта имеет вид С _РЕНТ = [+0,1; +0,5; +1]. Функции принадлежности треугольных чисел в этом случае имеют вид соответственно

Ц Z ( x ) = <

х + 1; -1 <  х <  0;

-х + 1; 0 <  х <  1;

I 0; ( х <  -1)v (х >  1).

R = max P ( a , a’ , a’’ ,..., a n ) = ^max 0< a <1

0 <  a' < 1

0< a n <1

B 2      ( B ‘ )² ( B ‘‘ )²         ( B n )²

“ 2 ML ‘ 2 M'L' ' 2 M"L" " " 2 M"L"'

Приведем пример использования данной модели для случая экспресс-оценки проекта по одному критерию (параметру).

Ц C ⁽ x ) = <

2,5 х - 0,25; 0,1 <  х <  0,5;

- 2 х + 2; 0,5 <  х < 1;

I 0; ( х < 0,1)v (х > 1).

На рис. 11 представлены графики функций µ _C ( x ), µ _Z ( x ) в одной системе координат для α –уровневого интервала неопределенности 0,5.

Средний риск окупаемости и рентабельности проекта в данном случае представляется возможным определить путем усреднения значений P(α) для множества выборок α–уровне-вых интервалов в пределах 0…1.

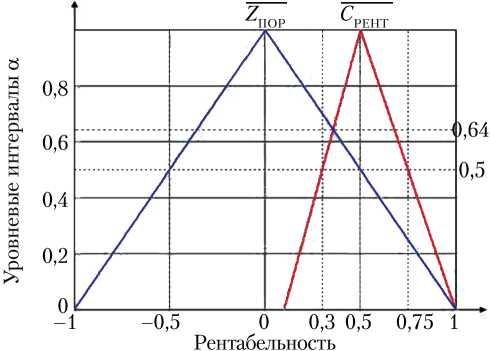
Рис. 11. Графики функций µ _C ( x ), µ _Z ( x ) в одной системе координат для α –уровневого интервала неопределенности 0,5

Методом математического моделирования получены значения максимального и среднего рисков инновационного проекта: R _max = 0,229, R _сред = 0,14.

Заключение

Приведенный научно-методический аппарат целесообразно рассматривать не как самостоятельный инструмент оценки степени рисков инновационных проектов, а в комплексе с другими инструментами управления рисками проектов, в частности, при создании (модернизации) перспективных космических систем и комплексов.

При применении представленного научнометодического аппарата в ракетно-космической промышленности необходимо учесть особенности проектирования ракетно-космической техники на ранних стадиях жизненного цикла космических систем (комплексов). Эти особенности заключаются в последовательном прохождении следующих этапов:

• •    подготовка технического предложения (аванпроекта);

• •    эскизное проектирование;

• •    разработка рабочей документации на опытные изделия комплекса и макеты.

Очевидно, что на данных этапах достаточно сложно давать прогнозные оценки степени различных видов рисков из-за ограничений объема априорной информации, в т. ч. по эффективности промышленной эксплуатации изделия в заданной временной перспективе, а следовательно, от реализации проекта в целом. В этой связи данный научно-методический аппарат (совместно с другими инструментами оценки рисков) позволит произвести начальное приближение в части отыскания возможных видов рисков внедрения инновационного проекта, их верификации и разработки эффективных мероприятий по их парированию.