Упругое проскальзывание в задачах печати под давлением

DOI:

Способы традиционной печати отличаются принципами создания печатающих и пробельных элементов на печатной форме и методами переноса краски на запечатываемый материал [1].

Сегодня возросла роль объективного оценивания качества печатной продукции, которое определяется взаимодействием компонентов триады: запечатываемый материал – краска – печатающее устройство. Поэтому оборудование, обеспечивающее точный перенос краски на поверхность материала, как и другие компоненты, отвечает за конечное качество оттиска [2].

В офсетной и флексографской печати для краскопереноса применяют упруго-эластичные материалы формного и офсетного цилиндров. Формный цилиндр покрыт гибкой формой, офсетный – композиционным офсетным резинотканевым полотном (ОРТП), имеющими высокую долю упругих деформаций [1–4].

В условиях оптимального давления между печатной формой и ОРТП в зоне соприкосновения при передаче краски возникают искажения в печатных элементах. Возникающие искажения статистически не определяются [1–4].

Устранение искажений осуществляется путем компенсации на стадии подготовки форм. Отсутствие статистических методов компенсации вынуждает определять искажения опытным путем [1–3].

Материалы и методы

Для определения параметров взаимодействия формного и офсетного цилиндров в офсетной печатной машине можно использовать контактную задачу Герца [5].

Натурные испытания проводились на печатной машине Heidelberg Speedmaster CD 74 (производство Германия) на инструментальном комплексе с использованием оптической системы измерения TECHKON RMS 910. Непосредственным измерением геометрии формы и площади меток регистра. Метка регистра записывается на калиброванной печатной форме и имеет абсолютно круглую форму диаметром ≈ 50 мкм. Оптической системой последовательно измеряются оттиски метки на резинотканевом полотне и бумаге.

На рисунке 1 представлена схема расположения цилиндров в печатной машине. Давление создается при сжатии упруго-эластичного ОРТП на фиксированную величину. Сжатие обеспечивается контактными кольцами цилиндров и толщиной жесткой подложки на цилиндре под ОРТП. Радиусы контактных колец и печатного цилиндра одинаковы [1–3].

Композиционное резинотканевое полотно устанавливается вровень с контактными кольцами путем подбора жесткой подложки (пленка, картон) с учетом остаточной деформации. Остаточная деформация учитывается при натяжении полотна и его приработке. Натиск в верхней печатной паре создает превышение жесткой металлической формы над контактными кольцами [2,3].

Давление в нижней печатной паре создается путем подведения нижнего печатного цилиндра к офсетному, где нулевая точка – это контакт печатного цилиндра с контактными кольцами офсетного цилиндра. Эта величина выбирается печатником в зависимости от состава, структуры и вида отделки запечатываемого материала. Определяющее условие – минимально необходимое давление, при котором происходит максимально возможная пропечатка всех элементов изображения [2, 3].

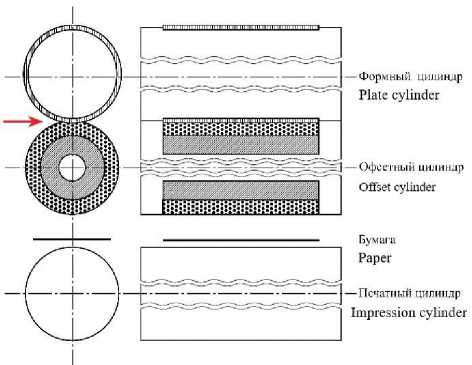
Рисунок 1. Схема печатной секции офсетной печатной машины

Figure 1. Scheme of the printing section of an offset printing machine

Соприкосновение контактных зон поверхностей печатного и офсетного цилиндров (на рисунке 1 обозначено красной стрелкой) примем как соприкосновение упругих параллельных полуплоскостей (рисунок 2). Полуплоскости могут изменять положение как жесткие тела. Постоянная внешняя сила сдавливает тела без изменения направления при изменении положения полуплоскостей. За границей зоны соприкосновения полуплоскости находятся на расстоянии друг от друга (отдалены) и не испытывают напряжений [2–5].

Различия радиусов печатного и офсетного цилиндров в зоне соприкосновения и одинаковая угловая скорость обеспечивают несовпадение линейных скоростей полуплоскостей. Скорости полуплоскостей формного и офсетного цилиндра – vt и vb соответственно. В зоне соприкосновения можно выделить области с длинами (11 и d3, где точки поверхностей проскальзывают друг относительно друга, и зона d2, где поверхности сцеплены и точки неподвижны относительно друг друга [4–5].

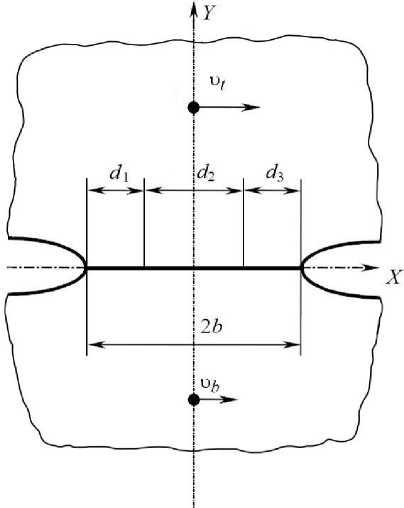
Рисунок 2. Соприкосновение упругих полуплоскостей формного и офсетного цилиндров

Figure 2. Contact of the elastic half-planes of the plate and offset cylinder

Дополнительные условия для решения задачи: ОРТП испытывает только упругие деформации, определяемые законом Гука; зона соприкосновения значительно меньше общих поверхностей цилиндров; поверхность ОРТП однородна по свойствам и натяжению на каждом участке. Определение трения в печатной паре офсетной печати с увлажнением пробельных элементов является спорным, но будет использоваться в дальнейшем, так как присутствует в классической контактной задаче Герца.

Для тела в состоянии равновесия сумма работ всех действующих на него сил равна нулю при всех возможных изменениях положения, принцип Лагранжа [6]:

N E = NA^ + N A ext (1)

где ∆ E – вариация энергии системы; ∆A int – вариация работы внутренних сил; ∆A ext – вариация работы внешних сил.

Вариация работы внутренних сил может быть представлена в виде

N A Lt = 3 [0.5Д£ ( G • Г 2 ++ 3 • e ² • k ) dV ] (2) где G – модуль сдвига, G = 0.5 E / (1 +μ ); Г – интенсивность деформации сдвига; 8 - средняя деформация, ε = ( ε x +ε y +ε z ) / 3; k – модуль объемной деформации, k = E /(1 – μ ); Е – модуль Юнга; μ – коэффициент Пуассона.

Участкам скольжения свойственно возникновение на поверхности касательных напряжений трения, помимо нормальных напряжений. Из-за неопределенности границ этих участков вариация работы внешних сил в уравнении (1) будет отлична от нуля и может быть определена как

^NA ext = X\\_Sj ^т ^ wjdSj = ³ [X , JI _Sj

т_:w_jdS_j   (3)

где τ j – касательные напряжения трения в зонах скольжения; j =  1.3 -соответственно зонам

(рисунок 2); w j – смещение точек поверхности в зонах скольжения; S j – площадь зон скольжения.

Касательные напряжения трения определяются через нормальные т = f -ст „ y=0

где f j – коэффициент трения в j -зоне; σ y= 0 – нормальные напряжения на контактной поверхности.

Таким образом, вариационное уравнение (1) примет вид

0.5 Jjj ( G • Г ² + 3 • e ² • k ) dV - v

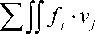
- 0 (4)

• 1.1    Область деформации

Определим систему координат с осями X и Y для участка соприкосновения. На участке соприкосновения полуплоскости упруго деформируются. Примем форму участка V соприкосновения как прямоугольную с длиной, равной длине участка соприкосновения, и высотой h – глубиной деформации, как показано на рисунке 3a. В качестве единицы длины используется половина длины участка соприкосновения.

• 1.2    Кинематически допустимое поле скоростей

Движение точек на участке соприкосновения будет происходить как по оси X, так и по оси Y. Причина – изменение скорости на разных областях участка соприкосновения. В области сцепления скорость точек равна нулю, а вне деформированного участка будет ∆v и - ∆v для полуплоскостей формного и офсетного цилиндров соответственно, где ∆v = ( v t – v b )/2 [8–10].

Таким образом, рассматриваемый участок можно разделить на области «замедления», «сцепления», «ускорения». Кинематически возможное поле скоростей рассматриваемого участка представлено на рисунке 3b [8–10].

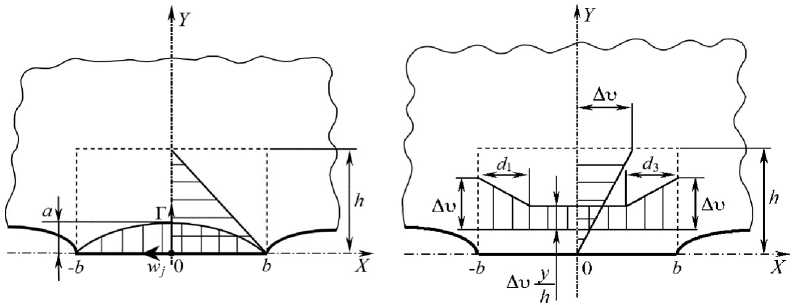
a)                                                              b)

Рисунок 3. Эпюра перемещений (a) и кинематически допустимое поле скоростей (b) в зоне соприкосновения

Figure 3. Epure of displaced (a) and kinematically permissible velocity field (b) in the contact zone

1.3 Расчет упругих деформаций

Учитывая постоянные изменения передвижения точек в зоне деформации линейные и угловые деформации могут быть определены:

^S x

- 2 ax l 1 -

^Y xy

- 2 ax 1 -

A v ,y .. x +1 .         .    ,

— • (y -1) • —,-1 <  x <-l + d ;

vh   d

■ — • (— -1),-1 + d < x <  1 - d ; v

Av zi У , x -1 1

— • ^{(1 -} 7) • T, ^{1 - d} < ^x < 1;

l v      h d

Sy =- a • (1 - x2) • 1; h s = 0;

y Y^ 'Yll, - 1 <  x <- 1 + d ;

hJ v   2 hd y i  Av 2 x + 2 - d

+--- , - 1 + d <  x <  1 - d :

h J v      2 h    ,

- 2 ax l 1 -

h J v

A v 4 d - 2 d ² - ( x - 1 )^:

2 hd

— ,1 - d <  x <  1;

Y yz = Y zx = 0.

Для упрощения расчетов примем длины областей «замедления» и «ускорения» равными: d 1 = d 3 = d .

Тогда энергия системы имеет следующий вид [11]:

Согласно энергетическому условию Губера-Мизеса, при значениях ∆v/v и a менее чем 10^–2 на участке соприкосновения отсутствуют пластические деформации, что ограничивает использование рассматриваемых уравнений [11].

1.4 Случаи скоростной асимметрии

Скорости полуплоскостей определяют появление следующих областей на участке соприкосновения: при ∆v = 0 (контактная задача Герца) на всем участке соприкосновения – только область «сцепления» поверхностей; при v t < v b присутствуют области «замедления» и «сцепления», зона «ускорения» отсутствует ( d = d 1 ≠ 0, d 3 = 0); при v t > v b присутствуют все области ( d 1 = d 2 = d 3 ).

При нормальной эксплуатации печатной машины реализуется только третий случай.

Когда области скольжения формируются в начале и в конце участка соприкосновения, минимизация функционала энергии (9) по неизвестным h и d приводит к следующей системе уравнений:

dE dh

E = 2 GB

1 - ^  [(Av^2 h(6 - 4d)16

1 - 2p j^ v J      915

4 p - 1 A v a ( d ³ - 4 d ² + 8)

+—-------------- +

1 - 2 p  v12

(A v Y 8 d ³ - 5 d ² - 60 d + 80

++

^ v J

4 .

+-• a2 • h - 2 f • f 1 - p  a (d4 - 3 d 3)    pA

'1 1 - 2 p     3 h      1 - 2 p ' ~ ' T

1 -p (Av7 6-4d   1 -p 16a2

1 - 2 ^ \~ ^J   ~ 1 - 2 p '-hid ⁺ ~

(A v Y 8 d ³ - 5 d ² - 60 d + 80

• - — \--5-------+=

I v J

• 1    - p  2 a ( d ⁴ -3 d ^J)

+f' 1^p —7—]

• 1    - p  4h  12d2 - 5d - 301]

1 - 2p ' 9+     20h2

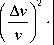
dE dd

4p-1 Av a(3d2 -8d) __

+1 - 2p ’ v '     12

Г 1 -p  2a(4d3 -9d2)   2p  AvJ

- f  d

[1 - 2p       3 h        1 - 2 p v JJI

В качестве примера на рисунке 4 пред-

ставлено изменение глубины проникновения

деформации и длины зоны скольжения от отно-

где B – полуширина участка соприкосновения

по оси Z .

сительной разности скоростей полуплоскостей для различных смещений их по направлению друг к другу (пропорциональных сдавливающему воздействию).

Аппроксимация результатов при различных значениях разности скоростей, сдавливающей нагрузки и коэффициента трения, получено выражение для определения длины зоны скольжения применимое в инженерных расчетах:

d = Wf —, (111)

v где: kμ = 2.024 – 4.094μ, ka = 1.1 – 26.5a, kf = 1.68 – 16.21f + 51.54f2, качество аппроксимации: 0,87 R2.

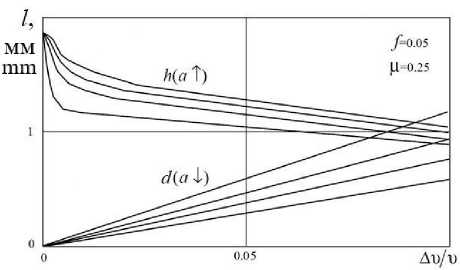
Рисунок 4. Влияние асимметрии скорости на глубину проникновения деформации h и протяженность скольжения d при a = 0.02; 0.05; 0.07; 0.1

Figure 4. The influence of speed asymmetry on the depth of penetration of deformation h and the length of sliding d at a = 0.02; 0.05; 0.07; 0.1

Различия радиусов печатного и офсетного цилиндров в зоне соприкосновения и одинаковая угловая скорость обеспечивают несовпадение линейных скоростей полуплоскостей. Скорости полуплоскостей формного и офсетного цилиндра – v t и v b соответственно. В зоне соприкосновения можно выделить области с длинами d 1 и d 3 , где точки поверхностей проскальзывают друг относительно друга, и зона d 2 , где поверхности сцеплены и точки неподвижны относительно друг друга.

Результаты

Полученные значения позволяют определять напряженно-деформированное состояние участка соприкосновения путем подстановки в уравнения деформации (5–8). Выявлено, что при увеличении разности скоростей, длины зон скольжения увеличиваются, а условная глубина проникновения деформации уменьшается до 30^50%. Это связанно с диссипацией энергии в зоне скольжения и перераспределением напряжений на деформированном участке (в частности – с увеличением нормальных напряжений по всей площадке соприкосновения).

Управляемое проскальзывание, при котором рассогласование скоростей участков поверхностей происходит исключительно в начале соприкосновения, может использоваться в расчетах для компенсации искажений в офсетной и флексографической печати. Оно будет создавать новые участки на соприкасающихся поверхностях цилиндров, но и может повлиять на появление сдвига элементов по всей площадке, когда протяженность области проскальзывания будет приближаться к величине 2Ь. Поэтому необходимо контролировать протяженность области проскальзывания, обеспечивая не превышение половины длины участка соприкосновения. Иначе, случится сдвиг элементов, что нарушит целостность печатной поверхности формы офсетной или флексографской в процессе печати. Увеличение нормальных напряжений на участке соприкосновения в области сцепления, как результат рассогласования скоростей, будет также способствовать более высокому качеству печати.

Обсуждение

Полученные значения позволяют определять напряженно-деформированное состояние участка соприкосновения путем подстановки в уравнения деформации (5–8). Выявлено, что при увеличении разности скоростей, длины зон скольжения увеличиваются, а условная глубина проникновения деформации уменьшается до 30^50%. Это связанно с диссипацией энергии в зоне скольжения и перераспределением напряжений на деформированном участке (в частности – с увеличением нормальных напряжений по всей площадке соприкосновения).

Управляемое проскальзывание, при котором рассогласование скоростей участков поверхностей происходит исключительно в начале соприкосновения, может использоваться в расчетах для компенсации искажений в офсетной и флексографической печати. Оно будет создавать новые участки на соприкасающихся поверхностях цилиндров, но и может повлиять на появление сдвига элементов по всей площадке, когда протяженность области проскальзывания будет приближаться к величине 2 b . Поэтому необходимо контролировать протяженность области проскальзывания, обеспечивая не превышение половины длины участка соприкосновения. Иначе, случится сдвиг элементов, что нарушит целостность печатной поверхности формы офсетной или флексографской в процессе печати. Увеличение нормальных напряжений на участке соприкосновения в области сцепления, как результат рассогласования скоростей, будет также способствовать более высокому качеству печати.

Заключение

Представленная методика расчета областей скольжения при соприкосновении поверхностей применима при исследовании других трибологических процессов непосредственного физического взаимодействия между взаимоперемещающимися поверхностями. В частности, управляемое проскальзывание упругих поверхностей на участке деформации при производстве высокоточных репродукций, в том числе денежных знаков, акцизных марок, при офсетной и флексографской печати.