Упругопластическое разрушение труб с поверхностной трещиной

В последние годы на магистральных газопроводах РФ отмечен рост аварийности связанный с стресс-коррозией. При обследовании участков газопровода Уренгой-Петровск протяженностью 1453 м было выявлено 744 стресс-коррозионных дефекта. Отдельные дефекты имели глубину до 7 мм и длину до 4,5 м. Ресурс работоспособности трубопровода определяется временем его эксплуатации до момента сквозного разрушения стенки. Еще более неопределенным является время зарождения порогового дефекта, способность к стабильному росту при эксплуатации магистралей, трубопроводов, теплотрасс, водоводов и сосудов давления. Разрушение магистральных трубопроводов, изготовленных из трубной стали класса прочности К-52, явилось следствием зарождения на наружной поверхности трубы продольных коррозионно-механических трещин, расположенных в нижней части трубы вблизи продольного сварного шва. Работоспособность трубопроводов во многих случаях обуславливается наличием в них концентраторов напряжений -трещин, рисок, царапин, каверн. В настоящее время недостаточно изучено распределение напряжений и деформаций в трубах с поверхностной трещиной. В этом случае задача становится трехмерной и, при учете пластических деформаций, развивающихся в вершине трещины, трудноразрешимой и актуальной.

Рассмотрено напряженно-деформированное состояние трубы с поверхностной осевой трещиной при плоско-напряженном состоянии. Применяя модель Панасюка-Дагдейла и деформационные критерии разрушения (критическое раскрытие трещины) получены аналитические формулы, дающие связь между характеристиками материала и разрушающим кольцевым напряжением трубы.

2.    Схематическое описание задачи

Труба считается бесконечной, с приложенным внутренним давлением перпендикулярным плоскости трещины. Трещина считается линейной, постоянной глубины. Из-за приложенного усилия трещина имеет тенденцию к раскрытию и деформации нетто-сечения, равно как и прилегающие зоны. Раскрытие трещины варьируется вдоль длины трещины и будет максимально в центре трещины. Предполагаем, что трещина вместе с некоторой окрестностью (пластической зоной) отсутствует, а силы, действующие в данной зоне, заменяются на граничные условия в соответствующей упруго-пластической задаче. Схема трещины дана на рис. 1. Разрез дан вдоль трещины, темно-серым показаны пластические зоны у концов трещины.

Математическую модель задачи можно описать в следующих терминах и предположениях.

• 1.    Труба имеет поверхностную осевую трещину.

• 2.    На трещину действуют растягивающие силы, которые при рассмотрении задачи заменяем напряжениями, действующие в нетто-сечении трещины.

• 3.    На обоих концах трещины растягивающие силы заменены напряжениями, действующими в кончиках трещины (пластической зоне).

  2a

  

  Рис. 1

  
  
3.    Критерий разрушения нетто-сечения поверхностной трещины

Если глубина трещины постоянна и материал идеально упругий, то силы, передающиеся через нетто-сечение трещины постоянны. С другой стороны если материал подвержен деформационному упрочнению, то эти силы есть функция от деформации и таким образом зависят от раскрытия трещины, достигая максимума в центре.

Для описания разрушения необходимо определить критерий разрушения нетто-сечения поверхностной трещины трубы. По аналогии с критерием разрушения, мы предположим, что,разрушение (распространение трещины) возникает когда:

• 1)    напряжение в центре трещины достигло критического значения для материала;

• 2)    раскрытие трещины в центре трещины достигло критического значения 8_С определенного для каждого материала.

4.    Аналитическое решение

На основании схематического описания задачи возможно теоретическое определение напряженно-деформированного состояния трубы с поверхностной трещиной (<7 - глубина, 21 - длина трещины, t - толщина стенки трубы).

Для эллиптических трещин при решении задачи используется конформное преобразование m             т)               о + ^    а + ^

плоскости [7] z = to\Q = n — где параметры п =----,т = ---- определяются через пара-

• V С)                   2 a-b

метры эллипса а (большая полуось) и b (малая полуось). В нашем случае для трещины считается, что малая полуось равна нулю. Это означает равенство т = 1, n = a 12.(0.

Мы предполагаем, что длина пластичной зоны равна действительной длине трещины 2Z тогда как длина трещины включая зоны пластичности у концов трещины равны 2a. Эти два параметра связаны соотношением / = acos(a) ,где a - есть вспомогательный параметр.

Граничные условия определяем так: напряжение на бесконечности равно кольцевому напряжению ав, функцию распределения напряжения в нетто-сечении поверхностной трещины, кото рая зависит от расстояния х от вершины до центра трещины, предела текучести <тг, предела прочности ав, напряжения пластического течения а = кхств предполагаем равной: к

Р^-^-1Х5-<а-к_га_ТХ^аХх11^^,                (1)

/=1

где к_х характеризует момент потери устойчивости (напряжение пластического течения ст) пластического деформирования участка около вершины трещины, учитывает коэффициент двухос-ности нагружения стенки трубы ти₀ и показатель деформационного упрочнения п степенной аппроксимации диаграммы деформирования; к₂ определяет границу локализованной пластической зоны и зависит от коэффициента поперечной деформации д . Исходя из условий аналитического решения задачи предполагаем симметричность функции напряжений (1), которая является полиномом четной степени (например, 2 и 4). На рис. 2 показаны распределения напряжения в нетто-сечении для случая полинома 2 степени (вариант 1) и четвертой степени (вариант 2). Предполагаем также, что эти силы распределены независимо от глубины листа. Соответствующее распре-

Физика

деление напряжения, которое будет использовано как граничные условия соответствующей плоской задачи упругости, равно ст(х) = P(x)l(d -t)> в добавлении предполагаем, что напряжение на

к концах трещины равно кгот, что означает равенство У а, = 1.

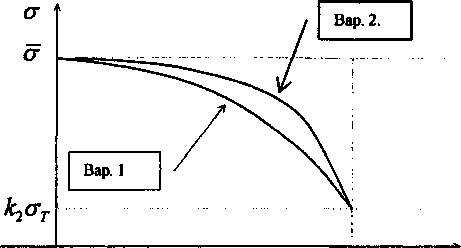
О Рис. 2                  I

Используя аппарат функций комплексного переменного Колосова-Мусхелишвили [1-2] и разбив задачу на три подзадачи - первая задача состоит в вычислении комплексных потенциалов Ф(О и Т(^) для напряженного состояния в окрестности трещины (напряжение на границе трещины равно нулю) и напряжение на бесконечности равно ов, вторая задача учитывает напряжение, передаваемое через нетто-сечение трещины, и последняя задача учитывает напряжение на кончиках трещины (в пластической зоне). В завершении для суммирования этих задач предполагаем, что результирующий комплексный потенциал может быть получен как сумма решений выше перечисленных задач с определенными весами, а именно мерой зоны действия соответствующих сил по принципу суперпозиции. Аналитические решения некоторых выше перечисленных задач можно взять из [1,2].

В качестве результата теоретического анализа получаются следующие два комплексных потенциала Ф«),Т(^) (громоздкие выкладки не приводятся):

a cos(a)

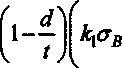
/=1 2

-— —+Г1-— )cos(a) + 2 U I t) ¹ J

аст_т d я¹ /

/ х(л dA к_х<т_в — k^cTj cij „_m +acos(a) 1-- .....15 ² ZdrZ^I x 1ы 2 _m=o

' ^-2/-2m+l     ^-2/-2m-l '

<2/-2m + l 2z-2m-l,

аФ*р d 2m t

z

a

^-е^Уа ^__e-²ⁱ“

_T 2< cos(a)

d_ t

-cos(a)ln

l-^2+2z

l-^2-2z^sin(a)

к _ pi к_хо_в-<к_хст_в

, \( Л ^A^A^R—kjC^T ^ч CL уД «тг#^. A x; +«cos(a) 1-- ^{1 B 2 r}Zd7E^C2”(2<-2m) x ‘ 2      ²_j=x 2 _m=0              ■

-— —+fl~—lcos(a) 2 U I t) '

2i-2m+l

d

t

aa_Td л t

•2i-2m-\ >

2/-2m+l 2z-2m-l

M^hf1-^^^]

2m ^[      (l-<²-2^sin(a)J

Аналогично подходу Дагдейла для исключения разрыва напряжений в концах трещины (^ = ±1), необходимо, чтобы коэффициент при (^2 -I)-1 в выражении (3) функции Т был равен нулю. Это приводит к следующему условию:

cos(a)L d

2 I1 /

к\ств-^ств

,=1 ² J ² V X t J У

aaT d л t

= 0. (4)

Остсемин А.А., Уткин П.Б.

Преобразовывая уравнение (4), получим:

cr_fl) . . 2a d ст_в d

—- cos(a)+--=-g—.

бГу              тг t ст у t

Из данного уравнения можно найти параметр а и далее размер пластических зон согласно модели Панасюка-Дагдейла о-1 = a(l-cos(a)).

Далее через комплексный потенциал Фф из уравнения (2) можно определить раскрытие трещины 5:

4       5

v = —-Ке(/Ф)=—,

Е      2

8 =

41ст_Т  (.  dV, ст_в  ,\^a_i^_nm(sin(f2i-2m + T)0')  sin((2/-2OT-l)0))

лЕ  V  t Д ^стт )ы^¹т4 I 2/—2m+l 2i-2m-l  )

d +— t

Уравнение на перемещение v легко получим из следующих соображений: учитывая, что рассматривается случай плоско-напряженного состояния и интересующая точка есть z = 0, можно, пользуясь уравнением для v, из [1] получить его в данном виде. Действительно, согласно [1, с. 149]:

*2.Ц№, у)+X*, у)) = к^ - гф\г^ -i//(z),                    (7)

Хо^-)+сг?Х<т')+(у(с) = /) + if₂,                              (8)

Л + Зи где к=——-

cos(0) ^ sin(<9 -«) cos(a) sin(<9+a)

sin 6-sin or sin 6* sin a

fi⁺ fl^{= z} ](^и ⁺^п)^⁸ • Если нам нужно раскрытие трещины в центре, то вы-о

числим значение функции v в точке 2 = 0. Складывая формулы (7) и (8) получим:

2Х« + zv) = (к + 1)Хо-) - (/] + iff).

Из формулы (9) сравнивая мнимые части, получаем:

v = (l/2//)((jr+l)Im(X<7»-/2).(Ю)

Далее заметим, что в случае линейной трещины и одноосного напряжения /2 = 0. Данное замечание можно обобщить на случай симметричной трещины и симметричного распределения напряжения. Итого (10) превращается:

у=^1т(Х<т)) = -^Ке(ф(о-))-(И)

2/z2/z

Осталось учесть, что в плоском случае надо провести замену Л->Я* = 22/z/(Z+2/z) после

-           г+1 . 2+//     4               ...., чего, преобразовывая----= 4-----—— = — из уравнения (11), получаем первую формулу (б).

2/z    /z(3/l+2/z) Е

Использование данной формулы возможно только на границе отверстия.

В уравнении (6) также учтено что £ = е’^е. Далее подставляя значение 6 = л^2 (что характеризует центр трещины) получаем:

^nE V V t )\ ®t )i=\       ¹             j

где

1 2/-2/И-1

Физика

Критическое раскрытие трещины 6_С есть характеристика материала [6]. Таким образом, формулы (4) и (12) устанавливают связь между геометрическими характеристиками трещины (длина и глубина), характеристиками материала (пределы текучести и прочности оу, <т_в) и разрушающим кольцевым напряжением ст₆.

Из формулы (12) можно определить параметр апо формуле:

a = 2tg 1

t 8слЕ л

exp — ^F d\ 81^

Т

d_ t

CF*p

Далее воспользовавшись выражением (5) определяем отношение а_в/сг_т :

2a d , л . d

---Hcos(a) 1 —

к sii

^CTT V ,=i   2

,2*

dA L dA

— + 1— cosa

t

t

Для проверки теоретического анализа были взяты экспериментальные данные, после чего проведено сравнение экспериментальных и аналитических результатов, вычисленных по формулам (13) и (14). В качестве примера приведены табл. 1,2. Экспериментальные данные табл. 1 взяты из работ Даффи А., проведенных в США [4], для стали Х-52 и из [5] - для российских труб большого диаметра, испытанных в ООО «ВНИИСТ» (Москва) (см. табл. 2). Критическое раскрытие трещины 8_С трубных сталей приведено в [6]. Средняя погрешность полученных результатов составила менее 6% (см. табл. 1) и 5,5% (см. табл. 2).

Данные для труб из табл. 1: R = 380 мм, / = 9,5 мм, 8_С = 0,27 мм.

Таблица 1

№ п/п	Марка стали	МПа	°"в» МПа	d!t	1, мм	Разрушающее давление (МПА) и погрешности вычисления (в %)
						ЭКС а9	_si ° 9	Я2 ° 9	погр. вар.1	погр. вар.2
1	Х-52	449,3	586,4	0,3895	180	372	363,03	370,56	2,41025	0,3867
2	-—....	449,3	593,5	0,3895	111	406	383,5	390,16	5,54095	3,9014
3	—	428,9	574,4	0,6	179	249	265,32	270,48	6,55605	8,6261
4	........	428,9	574,4	0,6	103,5	287	298,83	303,39	4,12269	5,7107
5	—-——	448,6	564,6	0,8105	36	390	350,97	351,83	10,007	9,7866
	Среднее								5,72748	5,6823

Данные для труб из табл. 2: 8_С = 0,27 мм; 08Г2ФБТ (R = 710 мм, t = 15,7 мм); Х-70 (R = 710 мм, t = 16,0 мм); 13Г1С (7? = 610 мм, / = 12,0 мм).

Таблица 2

№ п/п	Марка стали	°Т ’ МПа	°в> МПа	d!t	/, мм	Разрушающее давление (МПА) и погрешности вычисления (в %)
						^9	— 81 ° 9	—82 °9	погр. вар.1	погр. вар.2
1	2	3	4	5	6	7	8	9	10	И
1	AISI304	150,92	426,3	0,5	75	161,7	157,3	169,2	2,73754	4,6406
2	......	147	416,5	0,77	75	95,2	89,98	95,4	5,53663	0,1488
3	......	140,14	408,66	0,9	50	52,7	54,8	57,1	3,95382	8,2372
4	.....-	146,02	414,54	0,914	20	86	77,9	79,53	9,48442	7,5698
5	Среднее								5,4281	5,1491

Остсемин А.А., Уткин П.Б.

Окончание табл. 2

1	2	3	4	5	6	7	8	9	10	11
6	Х-70	435,4	622	0,6	225	317	286,95	293,37	9,48053	7,4556
7	13Г1С	402,2	519	0,5417	150	274	241,66	246,64	11,8046	9,9841
8	08Г2ФБТ	535,5	653	0,5172	260	328	333,07	338,41	1,54592	3,1734
9	08Г2ФБТ	546,9	667	0,5414	260	323	322,94	328,11	0,01797	1,5822
10	08Г2БТ	483	600	0,694	222,5	232	223,11	226,36	3,83149	2,4327
11	Среднее								5,33611	4,9256

В табл. 1, 2 приведены расчеты по двум различным вариантам для функции Р(х). В первом варианте функция взята равной Р(х) = х², во втором - равной Р(х) = х⁴. Используя такие таблицы для различных параметров трещины, можно решить обратную задачу, а именно найти критические параметры (глубину и длину) трещины для заданного кольцевого напряжения. Такая трактовка задачи даст возможность нормировать поверхностные трещины из соображений безопасной эксплуатации трубопроводов.

5.    Практическое применение полученных результатов

Для широко распространенной низколегированной марки стали 17Г1С-У <т_г = 360 МПа, <т_г = 520 МПа, a_e = cr_T(jJ_B)ln, где и = 2 - коэффициент запаса, с помощью предложенного теоретического аппарата при решении данной задачи построены ниже приведенные табл. 3, 4 с раскрытием трещины 8_С = 0,12 мм и 8_С = 0,09 мм по двум вышеописанным вариантам.

Если трубопровод подвергался внешним неблагоприятным воздействиям (старение, температура, длительный эксплуатация), то процесс разрушения характеризуется снижением раскрытия трещины с 8_С = 0,12 мм до 8_С = 0,09 мм. Поэтому получаются другие размеры поверхностного дефекта (длина трещины уменьшается).

Таблица 3

d/t	Длина трещины 2Z
	50	100	150	200	250	300	350	400	450	500
0,5	31,56	28,28	26,83	26,002	25,464	25,085	24,805	24,588	24,416	24,276
0,6	29,08	24,84	23,01	21,994	21,346	20,897	20,567	20,314	20,115	19,953
0,7	26,29	21,1	18,96	17,787	17,052	16,548	16,181	15,902	15,683	15,506

Таблица 4

d/t	Длина трещины 2/
	50	100	150	200	250	300	350	400	450	500
0,5	31,97	28,93	27,54	26,734	26,205	25,831	25,552	25,337	25,165	25,025
0,6	29,45	25,36	23,58	22,572	21,929	21,482	21,152	20,9	20,701	20,539
0,7	26,58	21,5	19,38	18,214	17,482	16,98	16,614	16,335	16,116	15,939

С точки зрения новой теоретической модели сугласно полученным табл. 3 и 4, задавшись внутренним статическим давлением и коэффициентом запаса 2, были вычислены предельная относительная глубина d/t и длина трещины 2/ (мм) при 8_С = 0,12 мм при различных кольцевых напряжениях ст_в (180 МПа и 260 МПа).

180 МПа

Таблица 5

	Вар. 1	Вар. 2
djt	0,7	0,7
21	250	275

260 МПа

Таблица 6

	Вар. 1	Вар. 2
ah	0,5	0,5
21	250	350

Физика

при 8_С = 0,09 мм

Таблица 7

	Вар. 1	Вар.2
djt	0,7	0,7
2/	180	220

Таблица 8

	Вар. 1	Вар.2
d/t	0,5	0,5
2/	200	250

Таким образом, с увеличением разрушающего кольцевого напряжения а_в труб большого диаметра с 180 МПа до 260 МПа относительная глубина d]t поверхностного дефекта снижается с 0,7 до 0,5 для обоих вариантов и значений раскрытия трещины 8_С. Когда 8_С снижается с 0,12 мм до 0,09 мм длина поверхностной трещины уменьшается с 250 до 200 мм по первому варианту и с 350 до 250 мм по второму варианту.

6.    Выводы

• 1.    Проведен теоретический анализ методом теории функций комплексного переменного Мусхелишвили по определению разрушающего кольцевого напряжения при вязком разрушении тонкостенных труб, сосудов давления с продольной поверхностной трещиной на основе раскрытия трещины. Показано хорошее соответствие новых теоретических формул и экспериментальных натурных гидравлических испытаний А. Даффи и российских ученых. Погрешность составила не более 6 %.

• 2.    Предложена новая математическая модель распределения напряжений в нетго-сечении поверхностной трещины трубы на основе напряжения пластического течения ст; коэффициента определяющего границу локализованной пластической зоны с учетом коэффициента поперечной деформации и деформационного упрочнения трубной стали.

• 3.    Получены нормы отбраковки поверхностных трещин трубопроводов, сосудов давления, теплотрасс, водоводов, которые полезны при их диагностике и капитальном ремонте. Максимальная относительная глубина трещины равна 70% от толщины стенки трубы, а максимальная длина трещины равна 180 мм при коэффициенте запаса равного 2.

• ■ - Работа поддержана грантом РФФИ 05-08-18179а.