Уравнение Левнера для отображений полос
Автор: Дубовиков Дмитрий Александрович
Журнал: Математическая физика и компьютерное моделирование @mpcm-jvolsu
Рубрика: Математика
Статья в выпуске: 11, 2007 года.
Бесплатный доступ
В работе получен полный аналог классического уравнения Левнера, описывающего стирание разреза, для конформных отображений полос с граничной нормировкой. Полученное уравнение позволяет дополнить известные радиальную и хордальную эволюции Левнера (SLE).
Короткий адрес: https://sciup.org/14968612
IDR: 14968612 | УДК: 517.95
Текст научной статьи Уравнение Левнера для отображений полос
В работе получен полный аналог классического уравнения Левнера, описывающего стирание разреза, для конформных отображений полос с граничной нормировкой. Полученное уравнение позволяет д шолнить известные радиальную и хордальную эволюции Левнера (SLE).
Уравнение Левнера возникло в знаменитой работе 1923 г. [2] в связи с попыткой решения проблемы коэффициентов. Геометрически оно описывало стирание разреза в терминах конформных отображений с нормировкой Римана. Впоследствии это уравнение обобщалось в связи с решением различных экстремальных задач. При переходе к граничным нормировкам возникли аналоги уравнения Левнера для полуплоскости (с гидродинамической нормировкой) и для полосы (при фиксации двух граничных точек, см. [5]). Поскольку такие обобщения ориентировались на создание вариационной техники в соответствующих классах конформных отображений, то конструкция, связанная со стиранием разреза, в них отсутствовала. С другой стороны, новые приложения уравнения Левнера, такие как SLE (см., напр., [3]), опираются на эту конструкцию.
В настоящей работе изучается вопрос получения полного аналога уравнения Левнера для полосы и конформных отображений с граничными нормировками. Здесь, в отличие от случая полуплоскости, мы не имеем возможности свести задачу к внутренней нормировке, поскольку изначально фиксируется соответствие двух граничных точек. Кроме того, продолжение отображений с использованием принципа симметрии приводит к бесконечносвязным областям.
Определение 1. Пусть П = {z 1 0 < Imz < >т}, f - конформное отображение полосы П в себя. Тогда (см., напр., [1, § 1-4]) для любого а е (0; 1/2) существуют конечные или бесконечные пределы
^(7)= lim (z-/(z)),
Re z^±oo
где z меняется в подполосе Па ={Z : Ct < Imz < (1 — 01^71 }, причем с ^j ) — с (7) (см. [5]). Эти пределы называют угловыми производными отображения f в бесконечно удаленных точках полосы П.
Определение 2. Совокупность всех конформных отображений j 1П —> П с конечными угловыми производными С" (У) обозначим через Т.
Определение 3. Через То обозначим подмножество функций f из Т, которые аналитически продолжаются через вещественную ось в полосу Q = {z : — к < Imz < Л"), оставляют инвариантной вещественную ось и удовлетворяют условию У (0) = 0. Конечность пределов С" (7) влечет условие Re f (z) —> ±со при Rez —> +оо .
Заметим, что класс Т замкнут относительно операции композиции. Более того, Т можно рассматривать как топологическую полугруппу относительно операции композиции и топологии локально равномерной сходимости. При этом То является подполугруппой.
Определение 4. Для каждой f из Т рассмотрим функционал у<Л = <ЛЛ-<ЛЛ-
Функционал у обладает свойством аддитивности: для ЛА gT выполняется r(Z ° АЛуШ + уШ-
Основным объектом исследований настоящей работы является семейство конформных отображений полосы П, образ которой получается из П вытиранием разреза. Более точно, пусть Г - простая жорданова кривая в полосе
п
с параметризацией ^ = ^/(/),
0 < / < /0,
где ^(/)еП при
O0. Обозначим через
Используя разложение gt в композиции отображений на области с «малыми» разрезами и мажорацию их «гиперболическими луночками», мы показываем конечность С (g,), а следовательно, и /(g,) . Таким образом, g( G То при всех Z G [O;Zoj. Кроме того, имеет место следующий результат.
Предложение 1. В принятых выше обозначениях у АЛ является непрерывной и строго монотонно убывающей на [0;Zo] функцией.
Сформулированное утверждение позволяет выбрать параметризацию разреза Г так, чтобы выполнялось соотношение /(g,) = Z0 — t, где t0 теперь будет равно /(g0). В определенном смысле эта параметризация аналогична левнеровской, где в качестве параметра выбирался конформный радиус расширяющейся области.
В принятых обозначениях основной результат работы можно сформулировать следующим образом.
Теорема 1. Семейство отображений gt 1 П —> D( с нормировкой из класса То и выбором параметра t согласно условию уЛ, ) ~ Zo— ^ ’ г^е ^ — ^ — кг дифференцируемо по t и является решением задачи Коши
д С — 1 1 ^^
где k^t) - непрерывная вещественнозначная функция и g, (g/ (Z)) = k^ — 1И .
Первый параграф данной работы посвяшен изучению свойств функционала У АР) . В частности, устанавливается, что близость уЛ') к 0 влечет близость J к тождественному преобразованию. Этот результат является основой для дифференцируемости g, . Кроме того, здесь приводятся альтернативные формулы для вычисления с" ^Л •
Во втором параграфе наряду с введением необходимых обозначений и определений устанавливается аналог интегральной формулы Шварца для специального класса функций и приводится ряд вспомогательных результатов, в том числе доказывается монотонность и непрерывность /(g,).
Третий параграф посвящен доказательству основного результата, теоремы 1.
-
§ 1. Свойства функционала Y^f^
Вначале теорема об эквивалентном определении Y^f) •
Теорема 2. Пусть f - конформное отображение полосы П в себя с конечными угловыми производными С^ ^JP тогда c+(/) = supln-^^-, zen Ime” '
Ime ^z) c-(/) = infln—-- 26П Imez
Доказательство: рассмотрим отображение ^*(^) = L° f ° И (z) , где н X е -l L^ = ~—: е + z
Г«) = 1п
in
где под логарифмом понимается непрерывная ветвь, принимающая значение 0 при ^ = 0.
Так как L конформно отображает полосу П на единичный круг А, то (р представляет собой конформное отображение единичного круга в себя. Кроме того, существуют угловые пределы
О) = lim^) = ±1, р'(±1) = lim^) •
В таком случае для угловых пределов справедливо
с" (/) = lim (z - /(z)) = limln Rez—>±«> ^->±1
<0-1
0 + 1
С учетом конечности С1 (У) получаем равенства с+(/) = 1п^(1),с-(/) = -1п^(-1).
Для аналитических в единичном круге функций, удовлетворяющих условию ^р(А) С А , определим функционал:
|1-ноГ M iw=sup
«»1-1<р«)1 i-й
2 "
Тогда по теореме Жюлиа-Каратеодори в случае конечного Р* (^) выполняется
равенство /?+(?) = $?’(1).
Замечая, что
Rel±£
|1-<К<)Г |1-Й _ R 1-^
^ИГН^Г Re' + ^-l-V^)
и подставляя в формулу (3) выражение для (р (1) , получаем после преобразований
с" (f) = In ^(1) = supin-——. zen Ime;
Аналогичными вычислениями, рассмотрев функционал
p" ^ = sup zgA
|1+ж£.МТ i -|^>|2' i - Й2
получаем необходимое выражение для С (/*).
Теорема доказана.
Отметим, что в случае f G То имеет место равенство
c*(/) = lim(x-/to). ГО
Л->±33
Поскольку f из То аналитична в Q и сохраняет вещественную ось, то условие конформности влечет f\x) > 0 при всех X G R. С другой стороны, используя принцип гиперболической метрики в полосе Q, получаем для всех Z 6 Q
|/'О)| , 1> cosIm(/(z)/2) cosIm(z/2)
Следовательно, 0 < f '(х) < 1, значит функция Й(х) = X — f (х) не убывает на вещественной оси, что с учетом равенств (4) для f G TQ дает
С-(/) S0 Решающим фактором в нашем исследовании, как и в оригинальной работе Левнера, является полугрупповая структура изучаемого класса функций. В частности, Левнером было установлено, что близость производной в нуле конформного отображения единичного круга в себя с нормировкой Римана к единице влечет «близость» отображения к тождественному. Следующая теорема устанавливает аналогичный результат для полугруппы То: близость уУУ) к 0 влечет «близость» отображения у к тождественному. Теорема 3. Пусть f G То, 0 < /(У) < 1пЗ, тогда для любого компакта К в полосе П существует константа МЦф такая, что для всех 2 G К \f(z)-z\ Доказательство. Пусть f еТ0, рассмотрим y(z) = У(г+С+(У)) - конформное отображение полосы П в себя. Легко видеть, что С+(У) = 0, С (У)<0, Y^H = Y^f) > 0. Конечность С1 (У) влечет Re f (z) —> +оо при Rez —>±°о . Как в (2), определим ф^') — L ° f ° LX (z) - конформное отображение единичного круга в себя. Существуют угловые пределы ^>(±1) = lim^9(^) = ±1, ^'(+1) = lim^z(^) и 5-»±\ ^->±1 ф'(У) • ф (~ 1) — 1, причем равенство достигается тогда и только тогда, когда ф - мебиусово преобразование единичного круга (см., напр., [4]). Тогда из условий С+ (У) = 0, С (У) < 0 и равенств (3) следует <У(1) = 1, ф\~ 1) > 1. Таким образом, граничная неподвижная точка ^9(1) = 1 является точкой Данжуа-Вольфа отображения ф. Тогда (см. [4], теорема 4) НгМ^И-п-!)-^. Учитывая, что ^ = £(z), ^Z> ° £(z) = £ о y(z) и ^>'(—1) = в1^, получаем а / - \ 24 (6) ^-ьЦ^М-^^ Отрезок Л, соединяющий точки 2 и f (z), целиком лежит в полосе П в силу ее выпуклости. Параметризуем отрезок X следующим образом: ^(/) = Z(z — y(z)) + /(z), О < Z < 1. Тогда легко получаем оценку V 2iew £(/(.))-£(;)=/ ole + Z l2 - /(z) • j Im 0 ew dt. Покажем, что значение Im у-------у- отделено от нуля, когда ^(Z) отделена от (е<(,) + Zj бесконечно удаленных точек полосы. Для этого рассмотрим отображение Легко видеть, что w(^) отображает двулистно полосу П на круг с центром в точке — Z / 4 радиуса 1 / 4. При этом точке W = 0 соответствуют две бесконечно удаленные точки полосы п. Если точки zJ^eK, где К - компактное подмножество полосы П , то точка ^(/) = ?(z — y(z)) + f(z} отделена от бесконечно удаленных точек полосы П при всех 0 < Z < 1. Значит, ее образ W^(/)) отделен от нуля, тогда Im ew 2 ’ где М х - некоторая константа, зависящая от выбора компакта К . С учетом последнего неравенства, получаем для любого ZEK £(/(z))-£(z)>z-/(z)-M.. С другой стороны, по принципу открытости SUp|£(z)| < 1, поэтому для любого Z Е К zeK 1 24 Тогда с учетом (6) и (7) получаем для любого Z Е К Мх Щ^-^<ке Теперь получим оценку для \f (z) — zj. Неравенство треугольника с учетом (5) дает |/(z) - z| < /(z - с+ (/)) - Так как при 2 Е К точка (z-сЧОеК1, где К' - компакт в полосе п , то из последнего соотношения с учетом (8) и равенства /(У*) = Ykf^ получаем для любого 2 Е К |/(Z)-Z|<(e",-1).M3 + Z(/), где М3 - некоторая константа, зависящая от выбора компакта К'. Так как при 0 < А < In 3 справедливо ех — 1 < (3/ In 3)х, то для любого 2 Е К I/O) - z| < Z(/) ~ • n, + z(/> = у<л • м. Теорема доказана. Таким образом, окрестность единицы в полугруппе То описывается в терминах функционала Y^f^ • Этот результат играет решающую роль в доказательстве дифференцируемости {g,} на [0; /0]. Для определения вида производной нам потребуется следующий аналог интегральной формулы Шварца. Лемма 1. Пусть f (2) = U^Z^ + iv(z) - аналитическая в П функция, непрерывно продолжающаяся в П , принимающая вещественные значения на вещественной оси, имеющая конечные пределы при Re 2 —> ±00 и удовлетворяющая условию Im f (2) > 0 при 2 Е П , тогда для всех 2 Е П 1 г ez -1 ег ^ № = - Н---7" 1---7 • VO + i7tW + /(°) • л; е + е 1 + е Доказательство. Не нарушая общности, можно считать f(0) = 0. По принципу симметрии Римана-Шварца f аналитически продолжается в Q = {2 : — ТС<1т2<тг}, где удовлетворяет условию (Im f (2))(1гП2) > 0. Рассмотрим /'’(<£') = f °1 ' (^), где <У = /(2) = (в* 2 — 1)/(е" 2 +1). Заметим, что /(2) конформно отображает полосу Q на единичный круг А, причем полосе П соответствует А+ = ^ ' 6, < 1, Im^' >0^. Тогда F^^) - аналитическая в А функция, непрерывная в А. Пусть F^^U^ViV^, тогда из интегральной формулы Шварца с учетом F(0) = / (0) = 0 получаем г(О = У-1£±^г(^)|^|. Условие (Im/(2))(lm2) > 0 влечет F^^ = F{^ для Q Е А, поэтому V(к-) = —V(zc) для К Е ЭА . Тогда с учетом аддитивности интеграла как функции множества получаем F(O = 4 ff^-^Vwi^l. 2^-ty^/c-< к-С) где 5A- = ;<:|<| = Umf>0}. Замечая, что к + £ к + £ _ - 2(к- - к^ к-(^ к-£ 1-(а + аК + <2’ получаем для любого е А Ж)=- f, Д^-ДД Ж) I * I • л91л-^к+к^+^ ^ = Z(z), пусть Z = X + 1у, тогда ie х/2 ге х1г к^к = W -1) 1 + еЛ 1 + ел dx. Подставляя эти выражения в формулу (10), получаем г эсле преобразований f^ = F ех'2 -1 ^,2+1 л j ez + ех --V^X + 1Л^Х. 1 + ех Лемма доказана. При изучении семейства {g,} перенос рассуждений в окрестность тождественного преобразования позволяет осуществить понятие эволюционного семейства (см. [5]). Определение 5. Двупараметрическое множество \w( s,0 < 5 < t < Zo } называется эволюционным семейством полугруппы То, если выполняются следующие условия: -•^ ^ То, 0 < 5 < Z < Zo; п. w, = w, ° w., ,0<$ <Т <1 iii. W, s (z) —>Z локально равномерно в П при / — S —> 0 . Пусть g, определены как ранее. Для 0 < 5 < ( < (0, положив W,$ (z) = g,' ° gs(z), получаем эволюционное семейство полугруппы То. Функция = g5(z) отображает П на Ds, в то время как W = g(' (Д) отображает Dt на П, причем Ds C_Dt. Поэтому при отображении gt"' область Ds соответствует полосе П , из которой удален образ части кривой Г, выделяемой параметризацией ^ = 1/^т), S^T^t. Обозначим этот образ через В( ( Таким образом, функция W = W, Дг) отображает П на П \ В, s. Пусть Als - множество граничных точек полосы П , соответствующих Bt s. Ясно, что At s целиком лежит на прямой Imz = Л. Обозначим Л(/) = g,"' ((/(О) ■ Заметим, что Z = A(s) е А, (, эта точка соответствует точке Q — iy(s) при отображении gs и концу разреза B(s, не лежащему на прямой Imz = ^, при отображении Wf (. Точка УР=Я(() - это конец разреза В1$, лежащий на прямой Im z = л. Лемма 2. Пусть Т g[s;(] и S Т Т, Z >L Г . Тогда множества Af s и B; s стягиваются в точку ^Т^) в соответствующих плоскостях. Кроме того, X - непрерывная на [0; Го] функция. Доказательство. Из теоремы Каратеодори о граничном соответствии при конформном отображении следует, что при фиксированном t и S Т / множество Bt $ стягивается в точку 2(/), а при фиксированном 5 и / 4 5 множество A, $стягивается в точку 2(5). Применение принципа длины и площади дает, что при Т е[5;/] и 5 Т Г, t V Т оба множества A, s и Bts стягиваются в точку А(т^ в соответствующих плоскостях. Покажем теперь непрерывность функции А^Г). По теореме Каратеодори о сходимости к ядру Wt $ (z) —>Z локально равномерно в П при / — 5 —> 0 . По принципу симметрии Римана-Шварца функция W 5 (z) продолжается до аналитической функции в П' = {z:О Так как при фиксированном 5 и t >L S множество Ам стягивается в точку 2(5), то для любого £■ > 0 найдется 6 > 0 такое, что при /€ [5^5 + 5] множество A,s сО£(20))сП', где Ое (2(5)) - Е-окрестность точки 2(5), достаточно малая, чтобы O.(2(s))clT. Обозначим С£ = ЗО^А^У Сс - компакте П', поэтому Wr;(z)—>Z равномерно на Се при t — S —> 0. Пусть z0 € С£ , тогда | ДО - 2(5)| < |2(5) - z0| + |z0 - w, s (z0 )] + |w, s (z0) - 2(0| < s + s + 4s = 6s. Таким образом, 2(/) непрерывна справа, аналогичным образом доказывается непрерывность слева. Лемма доказана. Обозначим Q' = {z = 2(0,0 ^ / < /0}. Заметим, что непрерывность 2(/) с учетом теоремы Кантора влечет следующее: множество Q - отрезок на прямой Imz — К. Пусть О = {z = 2(?) — 17Г,0< / < Zo} - проекция отрезка Q' на вещественную ось. Отметим монотонность /(w ) по / и 5 . Действительно, пусть Т G [у;?], тогда ^,.s СО = g? ° gs О) = g? ° gr ° gr ’ ° gs (Z) = W,.r ° ™r, CO • В силу аддитивности функционала у имеем y(w, $) = y(wiT) + y^W^v) / Значит, при фиксированном / и 5 Т / значение y(w,5) монотонно убывает до нуля. Действительно, в силу последнего равенства и того, что /(wr;) > О, получаем при 5 < Т < t Y^,^>y^,TY Аналогично при фиксированном 5 и t 4< У значение Y^ts^ монотонно убывает до нуля. Обозначим через С гиперболический (в полосе П) полукруг, вырезаемый из полосы п гиперболической прямой, проходящей через точки кх = А, + i.71, к3 = Х2 + ХК , Хх< Х2. За счет выбора точек хь х2 разрез В, s можно заключить в гиперболический полукруг С. Пусть Jc - конформное отображение П на П\С с нормировкой Rey(z)—>+оо при Rez —> ±оо,/(0) = 0. Обозначим h = W^ ° fc ■ В силу аддитивности функционала у выполняется /(w, $) + yQ^ = Y^fcVТ0ГДа y(wJ Элементарными вычислениями получаем, что /(/ ) = InА.с 4е,|"Х2 Так как при £ — £ —> 0 разрез Bt $можно заключить в гиперболический полукруг С, такой что Хг — Х1 —> 0, то имеет место y^W, $) — YVfc ) ~^ ^ ПРИt — S —>Q . Пусть теперь 0 < S < t < t0. Тогда /(gj = y^g, ° W, J = /(g$) + /(w, s), отсюда видно, что y^g,) - непрерывная и строго монотонно убывающая на [0; Го] функция. Поэтому можно считать, что параметризация кривой Г выбрана так, чтобы выполнялось равенство /(g,) = t.-t, тогда y(w, J = t-S. § 3. Доказательство теоремы 1 Покажем вначале дифференцируемость семейства {w, $} по t. Это будет следовать из локально равномерной липшицевости. Фиксируем 0 < 5 '"< /0 и точку z е К а П, где К - компакт. Тогда точка Wf s(z)gK’ сП, где К* — также компакт. Используя теорему 3 и условие параметризации /(w, 5) = / — 5 , получаем для любого Z € К к.* W - ^ьИ = Н^(и^(z)) - м^(z)| < М(К*) • ]г” - f|. Семейство {w, $} также дифференцируемо по 5. Действительно, фиксируем 0 ^ s' < s" < t < t0 и точку Z € К С П , где К - компакт. Тогда точка W, $. (z) G К* CZ П, где К - выпуклый компакт, следовательно k' (2) ■ w-x <»| = k' (z)- wm- lws-.s (^))| ^ maxk$- (z)| •M(K,y\s''- s'|. Найдем теперь вид производной. Рассмотрим семейство функций г ( X 2-W,+5 ,(z) Л (2) =-----------, о < 5 < 50. о Заметим, что у. аналитична в П, непрерывно продолжается в п, принимает вещественные значения на вещественной оси и имеет конечные пределы при Rez —> +со , В силу принципа максимума для гармонических функций Imy,(z)>0 при zgH. Таким образом, выполнены условия леммы 1 и имеет место представление (9), которое можно записать в виде г - 1 е1 f6 (2) = J—----7 ' -----7 • Дц8 (л), д е" + е 1 + е где Ц$ - мера, определяемая равенством с1ц6 (а) = - Im(y. (х + iTT^dx. л Из двух последних равенств и определения /(w, 5) с учетом (4) получаем 5=r(w.+s.t)=- /Мл о+^w • 71 R Таким образом, Ц5 - вероятностная мера. Заметим, что носитель меры (Л8 сосредоточен на проекции на вещественную ось множества Л1+8,. Но так как справедливо -А^61cQ\ то меры Ц8^ ^^8^8^ можно рассматривать как вероятностные меры на компакте Q. Известно, что пространство V(^) борелевских зарядов на Q изоморфно пространству, сопряженному к пространству С(0) непрерывных на Q функций (см., напр., [6], гл. ГУ, § 6): С(0* =V(g), причем для V eV(0 и / € С(0 v(/) = \f dv . По теореме Банаха-Алаоглу единичная сфера S G V(Q) .-слабо компактна (свойства слабой компактности см., напр., в [6], гл. V). Поэтому, если 8п 4 0, то Ц5 —> Д .-слабо и це8. Ц - вероятностная мера. Поскольку по определению .-слабой сходимости для любой f € С(5) имеет место Ц6 (f} —> Ц. Положив f = 1, получаем //(5) = 1, что с учетом ]Л Е S дает требуемое. Легко видеть также, что Slipp/Z = к(т), к(т) = Л(т) — 1л. Тогда из интегрального представления функций /^. и определения .-слабой сходимости следует, что при 8 4 О r ez -1 e ^-1 ekW ez ^ekw ‘\^еЦтГ Последнее соотношение позволяет определить вид производной по t: — w,, (z) = lim at ^° w,+<>.,(w, $(z))-w, $(z) ___^2^izL ._ЛЛ ew-(z)+ e^ j + ekW = У^,Лг\^ Далее, IV, 0 (z) = W,, ° W5 0(z), дифференцируя no S сложную функцию, получаем ^-iv,5(z) = -w;5(z)-r(z,s) OS Подставляя в последнюю формулу W^s (z) = g$ (z), приходим к уравнению (1). Теорема доказана.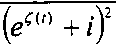
§ 2. Вспомогательные результаты
Список литературы Уравнение Левнера для отображений полос
- Alhfors L.V. Conformal Invariants. Topics in Geometric function theory. N. Y.: McGraw-Hill, 1973. 157 p.
- Lowner K. Untersuchungen uber schlichte konforme Abbildungen des Einheitskreises. I//Math. Ann. 1923. B. 89. S. 103-121.
- Rohde S., Schramm O. Basic properties of SLE//Ann. Math. 2005. Vol. 161. № 2. P. 879-920.
- Горяйнов В.В. Дробные итерации аналитических в единичном круге функций с заданными неподвижными точками//Мат. сб. 1991. Вып. 182. № 9. С. 1281-1299.
- Горяйнов В.В. Полугруппы конформных отображений//Мат. сб. 1986. Вып. 129 (171). №4. С. 451-472.
- Данфорд Н., Шварц Дж.Т. Линейные операторы. Общая теория. М.: Изд-во иностр. лит., 1962. 892 с.


