Уравнение состояния одномерной многочастичной системы с n-ступенчатым потенциалом взаимодействия

Н.Н. Гинчицкий, И.И. Клебанов

Методом Вертхейма получено точное аналитическое решение интегрального уравнения Перкуса-Йевика для одномерной системы частиц с п- ступенчатым потенциалом парного взаимодействия. На основании данного решения построено уравнение состояния одномерной системы частиц. Показано, что развитый метод позволяет строить аппроксимационные решения уравнения Перкуса-Йевика для любого непрерывного потенциала парного взаимодействия частиц.

В работе [1] было получено точное аналитическое решение уравнения Перкуса-Йевика для одномерной системы частиц с одноступенчатым потенциалом отталкивания («коллапсирующие» твердые сферы). В настоящей статье мы обобщаем полученные результаты на случай п- ступенчатого потенциала парного взаимодействия частиц, содержащего как области притяжения, так и области отталкивания. Потенциалы такого вида находят широкое применение при моделировании фазовых переходов типа «жидкость-жидкость» в коллоидных системах (в основном изучается двухступенчатый потенциал) (см., например, [2] и цитируемую там литературу). Ясно, что аналитическое решение уравнения Перкуса-Йевика для произвольного числа ступеней позволяет не только рассчитывать термодинамические характеристики конкретных систем, но и дает общий метод построения приближенных решений для непрерывных потенциалов взаимодействия.

Следуя обозначениям работы [3], рассмотрим одномерное уравнение Перкуса-Йевика:

г(х) = 1 - р j r(x')f (x')dx' + р J T(x')f (x’)t(x - х'^е^х - x'^dx'               (1)

Парная корреляционная функция g(x) и прямая корреляционная функция С(х) связаны с г(х) следующим образом

g(x) = т(х)е(х), С(х) = г(х)/(х),                             (2)

где е(х) = е^-^*\ /(х) = е(х)-1, р = \/кТ, р - плотность частиц, F(x) - потенциал парного взаимодействия.

Рассмотрим далее п -ступенчатый потенциал вида:
	оо,	х<1.
		I x.
	^2’	1 + ax< х < 1 + a2,
W = -	*3,	I + a2< х< 1 + a3,	(3)
	v„.	I + an_xn,
	0,	x>an.

После одностороннего преобразования Лапласа уравнения (1) получим аналогично [3]

F(s) + G(5) = 1^ -pVF(s) + F(-5)]G(5) - pY^ + pY<-s\            (4)

где

Гинчицкий Н.Н., Клебанов И.И.

Уравнение состояния одномерной многочастичной системы с п-ступенчатым потенциалом взаимодействия

I                 к-1

F{s) = yr(x)e^-sxdx + ^ ^p+i J T(x)e^-sxdx,

О             Р=оз к-1     SP+'”

G(s) = ^ £гр+1 j Ttx)e-sxdx + J r(x)e-sxdx, P=^     dpl*“k

°l                    a2

7(s) = ^y_xtx)e^-sxdx-i- ^y₂(x)e^-Bcdx + ...+ J y_k(x)e^-sxdx,

0                    ai l+a,

У_х(х) = е'£* j ^x’^x-x^dx', i = l,2,...,k.

l+x

I              k-l

К = 2 jt(x)dx + 2 ^ s"_{p +]} J T^dx,

O           P=O3p

8'p = e"PVp,fi"p =\-E'p,SQ ^1,8^1 + а^ = \,2,...,к.

Выражая G(s) из (4) и полагая g² = 1 + рК , получим:

Q2[S-F^-pYWpY^ kJ\S) =-------------------------------- \ + pF(s)+pF(.-s)

Следуя методу Вертхейма [3], введем функцию:

H(s) = s2G(s)

О2

¥_ + F(_s)_pY(s) + pY(-s)

-82[Y(s) + Y(-s)].

Из (6) и (7) получим

G(s) + F^ = ^— 2pY(s) - pG(s)F(s) - 4 H(,s) +    G(s) - p²G(s)Y(s) + p²G(s)Y(-s). (8)

8                            8           8

Асимптотическое разложение H(s) показывает, что Jits') = const согласно теореме Лиувилля. Тогда, раскладывая в ряд по s все функции (5) с учетом (7), получим

Произведя обратное преобразование Лапласа от (8), получим г(х) = С_о + С_хх, где коэффициенты С_о и С_х находятся из системы уравнений

(     к-1          )

С₀=(1 + рК) 1 + р^£'_р+х^^р) ”               V _Р=о J

[С^-рО + рЯ), где

^р+1

/оР)= j r(x)dx.

Используя общую форму уравнения состояния для жидкости или газа [4]

Р = pkT^drr

dVtr) dr

g(r).

(Н)

запишем уравнение состояния системы с п -ступенчатым потенциалом парного взаимодействия

Р = ркТ + £^

к-1

6"k5kTt3k) + £(4+1 -4)5рА5р) ,^ = о.

.                р=°                          _

Физика

Численный анализ уравнения состояния (12) показывает, что изотермы одномерной системы с и-ступенчатым короткодействующим потенциалом взаимодействия не содержит петли Ван-дер-Ваальса, что соответствует фундаментальной теореме статистической механики [4].

Полученное решение дает возможность строить приближенные решения уравнения Перкуса-Йевика для любого непрерывного потенциала взаимодействия частиц путем его аппроксимации п -ступенчатым потенциалом. Число ступеней выбирается исходя из требуемой степени точности. Приведем в качестве примера (см. рис. 1) изотермы одномерной системы частиц Леннарда-Джонса построенные на основании (12) путем аппроксимации потенциала

V(x) = 4e

х

12  / хб

। I X )

п -ступенчатым потенциалом.

На рис. 2 точками показана изотерма, соответствующая 5-ступенчатому потенциалу при температуре Т = 200 (в условных единицах). Для сравнения сплошной линией изображена та же изотерма, рассчитанная аналитически на основе вычисления статсуммы методом перевала [5]. Полученные результаты допускают обобщение на случай трехмерной системы.

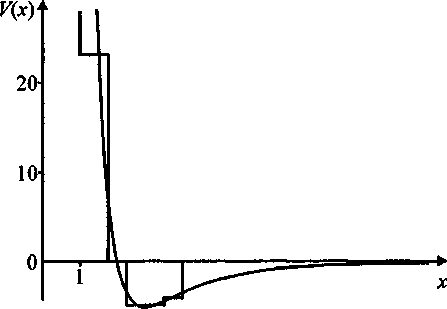
Рис. 1. Аппроксимация потенциала Леннарда-Джонса 5-ступенчатым потенциалом

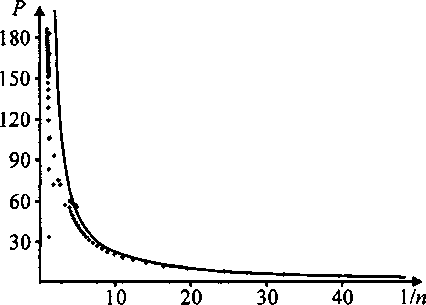
Рис. 2. Изотермы, соответствующие 5-ступенчатому потенциалу, Т = 200