Уравнение состояния полимерного композита, армированного S2 стекловолокном

Изучение поведения разнородных материалов в условиях динамической загрузки имеет жизненно-важное значение для многих областей применения композитов. Сложность построения уравнений состояния таких материалов заключается в том, что компоненты, входящие в состав композита, имеют разные механические и термодинамические свойства. Понимание реакции композитных материалов на ударно-волновые нагрузки имеет важное практическое значение в ситуациях, связанных со смягчением удара и взрыва, а также оптимизацией конструкций сооружений, имеющих дело с потенциальной опасностью динамического нагружения. В настоящее время множество различных материалов, начиная от металла, керамики и полимеров, как в монолитных, так и в композитных формах, используются для достижения поставленных целей. Наибольшее распространение получили стекловолоконные [1] и углерод-углеродные композиционные материалы [2].

В литературе имеется большой объем экспериментальных данных о распространении ударных волн в гетерогенных и композитных материалах [3-8]. Применение полимерных композитов, армированных S2 стекловолокном [9], в качестве важного компонента в системах, связанных со смягчением ударно-волновых нагрузок, требует углубленного и детального изучения поведения композиционного материала в широком диапазоне напряженных состояний. Для таких систем рассеяние, дисперсия и ослабление ударных волн играют решающую роль при определении тер- момеханической реакции среды. В частности, нелинейное поведение полимерного композиционного материала, армированного S2 стекловолокном (GRP), можно отнести к сложной структуре материала, развитию многочисленных повреждений в виде обширного расслоения, сдвига волокна, разрушения волокна при растяжении, большого отклонения волокна, микроразрушения волокна и локального напряжения волокна.

Несмотря на большой объем экспериментального материала, многие особенности ударноволнового нагружения композиционных материалов могут быть исследованы только с помощью математического моделирования. Для быстропротекающих процессов математическое моделирование очень часто оказывается единственным надежным источником получения достоверной информации. Для замыкания математических моделей актуальной остается проблема получения точных уравнений состояния [9].

Целью настоящей работы является разработка подхода к построению уравнения состояния S2 стеклопластиковых армированных полимерных композитов для описания экспериментов по ударно-волновому воздействию, представленных в работе [9], до уровней давления во фронте ударной волны 4,5 ГПа.

Уравнения состояния полимерного композита, армированного S2 стекловолокном

В зависимости от набора экспериментальных данных построение полуэмпирического уравнения состояния связующего [10-13] и минералов [13-18] начинается с выбора термодинамического потенциала. В данной работе таким термодинамическим потенциалом является свободная энергия Гельмгольца F(V , T ), которая наиболее простым и естественным образом связана с моделью строения вещества [10-13] и автоматически разбивается на тепловую и «холодную» составляющие:

F = U + Eov + kT £ ln(1 - exp( - h^. )), E ov = | £ h ^ . a             kT          ² a

Здесь U , T , h , к , <у _а, E_w - энергия межчастичного взаимодействия между атомами композитного материала, температура тела, постоянная Планка, постоянная Больцмана, частоты нормальных колебаний, энергия нулевых колебаний соответственно. В формуле (1) суммирование производится по всем частотам нормальных колебаний молекул, входящих в структуру композитного материала. Определив выражение для функции свободной энергии Гельмгольца F(V , T ), путем дифференцирования по объему и температуре данного термодинамического потенциала находятся все выражения для определения как измеряемых (давление), так и вычисляемых термодинамических характеристик (внутренняя энергия, энтропия) [19].

Не ограничивая общности, применим подход Дебая и перепишем колебательную часть свободной энергии Гельмгольца F(V , T ) свободной энергии в выражение (1) следующим образом:

F = U + E ov

(

+ 3 NRT — v ^D >

5 d

J ! ln(1 - exp( - ! )) d ! , o

здесь R , N , 6 D - универсальная газовая постоянная, поделенная на эффективную молекулярную массу композитного вещества ц , число атомов, характеристическая температура Дебая.

Интегрируя по частям третье слагаемое в выражении для свободной энергии F ( V , T ) , определенное равенством (2), а также вводя функцию Дебая D ( x ) [20]

x d!

exp ( ! ) - 1 ,

D ( x ) = A J ! ³

x 0

получим следующее выражение для свободной энергии Гельмгольца:

F = U + E_0V + 3 NRT ^ In ( 1 - exp( - x_D ) ) -

^{D ( x} D ) Л

3     ) ,

где x_D = 6 D / T .

Механика

Выражение для свободной энергии F(V,T) (3), позволяет определить давление P и энтропию S путем дифференцирования свободной энергии Гельмгольца по объему и температуре соответственно p=-dF 1

(д V ) T

-

д U

T V

-

dE OV. - 3 nrtd ( x_D ) d ^ ln ^ D j ^- dV          ^{v D)} d ( In V ) V

S = -

3 NR In ( 1 - exp( - x_D ) )

-

^{D (} x D )

- 3 NMRD ( x_D ) ^ .

При выводе формулы ( 5 ) было использовано свойство функции Дебая

D (x) =---- xD'(x), exp (x)-1  3

где штрих обозначает дифференцирование по характеристической температуре x .

Уравнения (3) и (5) позволяют определить выражения для энергии E и теплоемкости при постоянном объеме C :

E = F + TS = U + E₀ V + 3 NRTD ( x_D ) ,

C_V = 3 NR 4 D ( x_D ) -

3 xD exP(xD ) - 1

.

Вводя в рассмотрение коэффициент Грюнайзена по формуле y v = -d(In6d) ГD ( )     d (In V) ’ выражение (4) можно записать в виде

P =

—

д U д V

—

dE₀ V ₁ 3 NRT y d ( V ) D ( Xd )

dV

V

.

Исходя из определения энергии нулевых колебаний и учитывая разделение частот, получаем dE выражения для функций Eov и —0V-:

^o V     dV

1              9

eov = - E h®« = оnR^d ( v );

2 a       8

dE o v_ 9 NR Y d ( V W ( V )

dV    8

V

.

Дифференцируя выражение (3) по объему V c учетом равенства (9), получим выражение для давления P:

P = ³ NRT Y D ⁽ V ) ( d ( xd ) ) + Px , Px = -dU + 9 nrtyd ( v ) Xd j v , V                             д V 8

где второе выражение (10) определяет холодную составляющую давления композитного материала.

Объединяя давление нулевых колебаний с тепловой частью давления, преобразуем первое равенство (10) к следующему виду

P = 3 NRT y d (V ) p (D ( Xd ) + ³ Xd ) + P_c P c = -

.

8                д V

Подставляя выражение для энергии нулевых колебаний в равенство (6), получим следующее выражение для определения внутренней энергии

9   „

E = U + - NR 0 ( V ) + 3 NRTD ( x_D ).

Объединяя второй и третий члены правой части последнего уравнения, получим выражение для определения внутренней энергии

. 3 ,

E = U + 3 NRT ( D ( x_D ) + - x_D ).

Выражая второй член правой части уравнения (12) через внутреннюю энергию E и энергию меж частичного взаимодействия U и подставляя полученное равенство в уравнение (11), получим уравнение состояния в форме Ми–Грюнайзена

P - Pc = Y d (V ) p ( E — U )                               (13)

Для полимерного композиционного материала, армированного S2 стекловолокном, в работе [8] на основании экспериментальных данных была получена зависимость скорости ударной волны D от массовой скорости полимерного композиционного материала, армированного S2 стекловолокном, за ударной волной u :

D = a + bu = 3,228 + 0,996 u ,                                 (14)

где a и b – постоянные значения, определенные из экспериментов по ударно- волновому нагружению полимерного композиционного материала, армированного S2 стекловолокном. Выражение для скорости ударной волны (14) позволяет построить ударную адиабату полимерного композиционного материала, армированного S2 стекловолокном в виде:

P = p ₀ a ²(1 - x )/(1 - b (1 - x ))²,                                  (15)

где x = p ₀/ p . Для уравнения Ми-Грюнайзена (13) построим ударную адиабату (адиабату Рен-кина–Гюгонио). Соотношение, связывающее внутреннюю энергию и давление за фронтом сильной ударной волны, имеет следующий вид

Р,

E - Eо = 2 (Vo — V), где E,P,V – значения внутренней энергии, давления и удельного объема за фронтом ударной волны соответственно, Eo, Vo значения внутренней энергии и удельного объема до фронта ударной волны.

Выражая внутреннюю энергию E из уравнения (13) и подставляя в последнее уравнение, получим уравнение для адиабаты Ренкина–Гюгонио

P = ( Pc + Y d (V ) Р (E o — U ))/(1 — 0,5 y d (V ) p (V — V )) .                 (16)

Выражение для коэффициента Грюнайзена в дальнейшем было принято в виде, полученном в работе [21, 22]

Y d (V ) = Y o ( P / P o),                                      (17)

где Y _o — значение коэффициента Грюнайзена при начальной плотности р ₀ равной 1,959 г/см³ [8]. Для определения начального значения коэффициента Грюнайзена y ₀ рассмотрим предельный случай, когда давление P стремится к бесконечности, и определим предельные значения плотности p , или удельного объема V . Из уравнения (15) следует, что давление стремится к бесконечности, когда знаменатель равен нулю. Таким образом, из равенства

• 1    - b (1 - x ) = 0, следует, что

• x,= (b -1)/b.                                          (18)

Из уравнения Ренкина–Гюгонио (16) можно определить начальное значения коэффициента Грю-найзена при условии стремления давления к бесконечности в точке x , . Из равенства нулю знаменателя в уравнении (16)

1 - o,5 Y o(1 - x , ) = 0, получаем, что начальное значение коэффициента Грюнайзена связано с параметром b экспериментальной ударной адиабаты следующим образом:

Yo = 2 b.(19)

Таким образом, уравнение Ренкина–Гюгонио можно представить в следующем виде:

P = (Pc + 2bpo(Eo -U))/(1 -b(1 -x)).(20)

Сравнение выражений для описания холодной составляющей давления и внутренней энергии, полученных в работе [23], с уравнением Винета [24], показало [23], что эти составляющие могут быть представлены следующим образом:

Pc = 3poCo2 (x-(m+1) - x-n+1)),(21)

Механика

U = 3 C 2

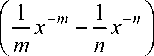
где C ₀ - объемная скорость звука, равная 2,6 км/с [8]. Из равенства нулю при x = 1 экспериментальных (15) и расчетных (20) значений давления на ударной адиабате следует, что

E о = U о = 3 C о² 1I .                                    (23)

V m n )

Для определения значений m и n, потребуем равенства первой и второй производных по x на экспериментальной (15) и расчетной (20) ударных адиабатах в точке x = 1. Получим систему из двух уравнений

cP ex	_ d P calc _	. d Pc
d x	d x	d x
6 2P ex	_ d 2 P calc	_ d Pc
d x 2	d x 2	d x 2

,

где P_ex и P_calc определяются из уравнений (15) и (20) соответственно.

Подставляя в уравнения (24) и (25) выражения для соответствующих производных давления на ударных адиабатах, определенных равенствами (15) и (20) по x , получим следующую систему уравнений для нахождения параметров m и n :

a ²/(3 C 2) = m - n ,                                     (26)

(4 a ² b ) /(3 C ₀²) = ( m + 1)( m + 2) - ( n + 1)( n + 2).                       (27)

В результате решения системы уравнений (26) и (27) были получены следующие значения: m = 0,7567, n = 0,2429. В таблице приведены значения давлений на экспериментальной [8] и расчетной ударной адиабате (20).

Сравнение экспериментальных и рассчитанных значений давления

£	x	Pex , ГПа	P calc , ГПа
0,01	0,99	0,2083	0,2083
0,02	0,98	0,4250	0,4252
0,03	0,97	0,6507	0,6512
0,04	0,96	0,8857	0,8869
0,05	0,95	1,1304	1,1377
0,06	0,94	1,3854	1,3895
0,07	0,93	1,6511	1,6576
0,08	0,92	1,9280	1,9380
0,09	0,91	2,2168	2,2312
0,10	0,90	2,5179	2,5387
0,11	0,89	2,8319	2,8580
0,15	0,85	4,2320	4,2588

Приведенные в таблице данные показывают, что расхождение экспериментальных и расчетных значений давления на ударных адиабатах менее 1 %.

Выводы

• 1.    Предложенный в данной работе подход позволил получить уравнение состояния, позволяющее с высокой точностью воспроизводить экспериментальные данные по ударно-волновому нагружению полимерного композиционного материала, армированного S2 стекловолокном.

• 2.    Преставление уравнения состояния в форме Ми–Грюнайзена позволяет применять данную методику и к другим композитным материалам, для которых известны экспериментальные ударные адиабаты и объемная скорость звука при нормальных условиях.