Уравнения Бельтрами, вырождающиеся на дуге

Пусть в односвязной области D С C задано уравнение Бельтрами (см., например, [2])

^f z ^{( z} ) = l ⁽ z)^f_z ^{( z}).

При | |(z) | < 1 п.в. в D уравнения Бельтрами наиболее изучены. Этот случай называется в дальнейшем классическим (см., например, [11]).

Хорошо известно [2, гл. 2], что справедливость условия

ess sup h(z)| < 1, D‘ для произвольной подобласти D b D, влечет существование гомеоморфного решения w = f (z) Е ^lOc (D) уравнения (1), при этом z = f-1(w) Е Ж^2(f (D)).

Уравнения Бельтрами в классическом случае являются одним из средств описания квазиконформных отображений и их обобщений [9]. В этой связи напомним, что коэффициент |(z) = fz(z)/fz(z) называется комплексной дилатацией отображения f (z) Е Ж \'© D). Его задание эквивалентно заданию п.в. в D поля распределения характеристик Лаврентьева (p(z), 0(z)), при этом связь между ними следующая (см. [1, c. 7]):

• ¹            —        = ¹ + | ^^{( z ) |}

• У(2)      ₂argHz)+₂ , ^{p ( z )}    1 -| ^( _г)| ,

^(z) = - pp .    .                                                     (3)

Отображение w = /(z), первая характеристика которого в D п.в. удовлетворяет условию

p(z ) < Q = const,                                 (4)

называется Q- квазиконформным . Если условие (4) выполняется в D локально, то отображение называется локально квазиконформным . Условие (2) эквивалентно условию локальной квазиконформности.

Непрерывную функцию / (z) Е ^ lO^ D), удовлетворяющую уравнению (1) п.в. в D, будем называть решением данного уравнения.

Пусть существует замкнутое относительно D множество Е С D меры mes ₂ Е = 0. Если непрерывная в D функция / (z) является решением уравнения (1) в D \ Е , то функцию / (z) будем называть решением с особенностью Е данного уравнения.

Замечание 1. При этом неизвестна принадлежность / Е ^ lO ’ _c ² (D).

В случае |^p (z) | < 1 п.в. в D гомеоморфные решения не меняют ориентацию, а в случае |^p (z) | > 1 п.в. в D меняют. Эти случаи уравнения Бельтрами различаются лишь формально. Интерес представляет ситуация, когда одновременно существуют подобласти D, в которых п.в. выполнено |^p (z) | < 1 и подобласти D, в которых п.в. |^p (z) | > 1. В этом случае говорится, что уравнение Бельтрами имеет переменный тип. Его решения описывают отображения со складками, сборками и т. п.

Задача исследования уравнений Бельтрами переменного типа ставилась Л.И. Вол-ковыским [3]. Некоторые продвижения в этом направлении имеются в работах [11–13].

В наших недавних работах [5; 6] была изучена связь между строением решений классических уравнений Бельтрами и уравнениями Бельтрами переменного типа. Именно изучение уравнения (1) в общем случае было связано с изучением классического уравнения Бельтрами

/ г ^{( z )}= ^p * ^{( z ) /} _z ^{( z )},                                         ⁽ 5)

с комплексной дилатацией

*^ I ^^{( z )} ^ ^    । ^1/^ ^{( z} )

при Hz) <  1, при |^p (z) | > 1.

Это уравнение называем в дальнейшем уравнением, ассоциированным с уравнением (1). Очевидно, |^p * (z) | < 1 п.в. в D, причем в классическом случае уравнения Бельтрами ассоциированное уравнение совпадает с самим уравнением, так как ^(z) = ^p * (z).

Замечание 2. Связь между уравнениями Бельтрами переменного типа и ассоциированными уравнениями Бельтрами впервые отмечена в [8], а сам термин был введен нами в [5]. В этих работах показано, что складчатые решения уравнения Бельтрами переменного типа получаются из решений ассоциированного с ним уравнения с помощью дополнительной суперпозиции с функцией Бора В (z) = х- 1 + г | ж ₂ | . В связи с этим представляют интерес результаты об ассоциированном уравнении в терминах первоначального.

Далее будут использоваться терминология и обозначения работы [5], напомним их.

Пусть имеется некоторая функция / (z) : D ^ R. Если существует функция К (z) Е Е W ^1,2 (D) такая, что /(z) <  К (z), то функция /(z) называется W ^1,2 -мажорируемой в D. Если /(z) является W ^1,2 -мажорируемой во всякой подобласти D b D, то говорят, что / (z) является локально W ^1,2 -мажорируемой в D. В дальнейшем для краткости вместо «локально W ^{1 , 2} -мажорируема» будем писать «W _l Oc ² -мажорируема».

Пусть D С C — односвязная область и v = Т(z) : D ^ Т(D) С C — некоторый гомеоморфизм, сохраняющий ориентацию. Определим функцию max|z‘-z|=r |Т(У) - Т(z)|

Qt(z)   г™ min|e,_|=, |Т(z‘) - Т(z)| и замкнутое относительно D множество

Е = {z : z Е D, sup    Q _t (z ‘ ) = + то для всякого круга B _r (z) } .

z ‘ e B _T ( z ) D D

Известно [1, гл. 1, §4], что если Q _t (z) <  + то всюду (то есть при Е = 0 ) в D и Q _T (z) < Q = const п. в. в D, то отображение Т (z) Q-квазиконформно в области D. Это означает, что при Е = 0 отображение Т (z) локально квазиконформно в D \Е .

Множество Е будем называть множеством вырождения отображения Т (z).

По Т (z) определим класс функций

Т * W 02 (D) = { / (z ) = ^(Т (z)), где ^ Е W^ (D)) } .

Заметим, что в случае Е = 0 отображение Т (z) локально квазиконформно в D и, следовательно, Т (z) Е W^^D). Поэтому, в силу инвариантности классов W^ C при квазиконформных отображениях (см., например, [4, гл. 5, §4, п. 4.1, теорема 4.2]), заключаем, что Т * W lO ^, _C 2 (D) = W l0c2 (D). Следовательно, при Е = 0 , если / (z) Е Т * W lO^,2 (D), то /(z) Е W l0c2 (D \ Е).

Пусть 5(t) — положительная непрерывная при t = 0 функция, имеющая интегрируемую особенность в нуле. Определим комплекснозначную функцию

F s (z) = / 5 (^ 1 ) + гх 2 ,

где

t

/ 5 (t) = j 5(т)dr.

Градиент произвольной вещественной функции /(z) в точке z Е D в дальнейшем отождествляем с комплексным числом V /(z) = / _{Ж 1} + г/ _ж 2 . В соответствии с этим также пишем V /(z) = / _Ж 1 - г/ _Х 2 .

1.    Уравнения с вырождением на линии

В работе [5] были получены результаты о существовании и единственности решений ассоциированного уравнения Бельтрами, вырождающегося на дуге. Дадим их формулировки.

Пусть существует жорданова дуга Е С D, делящая область D на две односвязные подобласти D 1 и D 2 , причем на Е уравнение (1) вырождается, а характер вырождения описывается следующими условиями (B1), (B2).

(B1) Справедливо представление

ЫХ = 1 + M (z)5(H (z)), где M(z) — измеримая, п.в. конечная в D функция; 5(f) — непрерывная функция, такая, что 5(f) > 0 при f = 0 и 5(0) = 0; H(z) G С(D) О WlO,2(D), причем VH(z) = 0 п.в. в D и H(z) < 0 в Di, H(z) > 0 в D2.

(B2) Существует непрерывная функция Z (z) G V lO^ D) такая, что отображение

J (z ) = H(z) + %Z(z) G С (D) П W^(D)

является локально квазиконформным гомеоморфизмом D на J (D), сохраняющим ориентацию.

Замечание 3. Сказанное не означает, что Е совпадает с множеством всех точек, в которых уравнение вырождается.

Из условия (B1) следует, что H(z) = 0 — уравнение кривой Е.

Пусть в дальнейшем 1 1 (z) = ^{J ( z} ).

8 ( H,Z ) д ( ж 1 ,Ж 2 )

= H _{X 1} Z _{X 3}

-

H _{X 2} Z _X 1

— якобиан отображения

Очевидно в условиях (B1), (B2) представление (8) не единственно. Следующие теоремы 1, 2, доказанные в [5], указывают на некоторые соотношения между функциями M, 5, H, Z, при которых существует гомеоморфное решение c особенностью Е, уравнения ассоциированного с уравнением (1) и дают описание структуры этих реше- ний.

Теорема 1. Предположим, что выполняются условия (B1), (B2) и для всякой подобласти D' b D можно указать функцию К (z) G Ж ^{1 , 2} (D ' ) такую, что

/I

D ’

|V K (z) | ² 5(H)

dx 1 dx ₂ <  + то ,

причем для п.в. z G D

| M (z) | 5 ² (H)

.        VZ ² ,      1

^{M ( z} )    V Z  ⁺ | M (z ) |

< К (z).

Положим T (z) = F (J(z)) . Тогда существует гомеоморфизм w = /(z) : D ^ ^ /(D) c C , для которого справедливы утверждения:

• ( i )    / (z) есть решение с особенностью Е уравнения, ассоциированного с (1) ;

( ii ) / (z) G T * V ic ² (D) , / ^-1 (w) G Ж ₁ 0с ² (/(D \ Е)) ив представлении

^{/ ( z} ) = f ^{( T ( z ))} = f ⁽ F 8 ^{( J ( z )))}

отображение ^ имеет W^c ² -мажорируемую первую характеристику.

Гомеоморфизм w = / (z) единственен с точностью до конформного отображения в w -плоскости.

Теорема 2. Предположим, что выполняются условия (B1), (B2) и функция 1/5(t) имеет интегрируемую особенность в нуле. Кроме того, предположим, что для всякой подобласти D' b D можно указать функцию К(z) Е W ^1,2 (D ' ) такую, что

/I

D ’

\v к (z) \ ² 5(Н )

dx 1 dx ₂ <  + то ,

причем для п.в. z Е D

___1___ ___ - VH \М(z)\52(H ) М ( ) VH

2           1                  . + \М (z) \<К ( z ) .                  (П)

Положим Т (z) = F i (J (z)) . Тогда существует гомеоморфизм w = /(z) : D ^ ^ /(D) с C , для которого справедливы утверждения:

( i ) / (z ) есть решение с особенностью Е уравнения, ассоциированного с (1) ;

( ii ) / (z ) Е Т * W lOc ² (D) , / ^-1 (w) Е W l ¹ _o c ² (/ (D \Е )) ив представлении

/ (z) = У(Т (z)) = HF 1(J(z))) о отображение у имеет WlOC-мажорируемую первую характеристику.

Гомеоморфизм w = / (z) единственен с точностью до конформного отображения в w -плоскости.

Главной целью нашей работы является выяснение геометрических условий существования и единственности решений ассоциированного уравнения.

2.    Геометрический смысл условий (9) и (11)

Пусть для ^(z), кривой Е и области D выполняются условия (B1), (B2) предыдущего раздела и, кроме того, кривая Е локально спрямляема, а функция ^(z) непрерывна в п.в. точках кривой Е .

Замечание 4. Если речь идет о Е , то «почти всюду» рассматривается относительно линейной меры.

Рассмотрим условия теоремы 1. Предположим градиент VZ (z) непрерывен в п.в. точках Е , а якобиан I 1 (z ) > 0 п.в. на Е .

Зафиксируем произвольную подобласть D ' b D так, что D ' Q Е = 0 . Тогда из неравенства (9) для п.в. z Е D ' , получаем

M^{z) —}

V Z (z)

VZ (z)

< К (z) \ M (z)\d(H (z)).

Известно (см.: [10, §6]), что множество {z : z Е D, lim К(z') = +то} имеет z’^z линейную меру 0. Отсюда следует, что для п.в. z0 Е Е найдется радиус г = r(z0) > 0 такой, что

ess sup К (z) < + то . В _Т ( z o ) n D ’

Пусть z ₀ Е Е — произвольная точка непрерывности p(z) и V Z (z), в которой выполнено (14), I 1 (z 0 ) >  0, а к Е существует касательная.

Непрерывность p(z) в точке z ₀ в силу представления (8) влечет | ^(z ₀ ) | = 1 и

lim М(z)5(H (z)) = 0. z > z o

Выберем последовательность точек z_Tl Е D', z _n ^ z ₀ так, чтобы на ней выполнялось неравенство (13) и последовательность К(z_n) была ограничена. Тогда, учитывая (15), непрерывность ^(z ) и V Z (z ) в точке z ₀ , из (13) получаем

M^{( z} o ) -

VZ (z o )

VZz)

1- fl!  VZ (z„)\

•^ ^^(z" > -Wf)

= 0 .

Тем самым п.в. на Е

^ ^{( z}) -

VZ (z )

VZ (z )

= 0 .

Имеем соотношение

VH(z)VZ (z) - VH(z)VZ (z) = — 2iI i (z).

Так как I 1 (z) = 0 п.в. на Е , то с учетом (16), из предыдущего равенства, п.в. на Е вытекает соотношение

VH(z)VZ(z) — VH (z) ^(z)VZ (z) = 0.

Деля его на — iVZ(z) = 0, для п.в. z Е Е получаем iVH (z) + iVH (z) ^(z) = 0.

Так как вектор iVH(z) направлен по касательной к Е в п.в. точках Е, то п.в. на Е выполняется условие dz + ^(z )dz = 0,                                (17)

если dz направлено по касательной к Е .

В случае теоремы 2, при аналогичных ограничениях на Е, p(z), VH и I1(z), мы придем к условию dz + ^(z )dz = 0,                                (18)

где dz направлено по касательной к Е , выполненному п.в. на Е .

Дадим геометрическую трактовку соотношениям (17) и (18).

Пусть (p(z),6(z)) — распределение характеристик Лаврентьева, отвечающее комплексной дилатации ^*(z). Так как

1 + l M * (z) | = 1 + | M(z) |

1 — |^*(z)|     |1— Mz)||, то представление (8) означает, что p(z) = то при z Е Е,

или, в силу (3), / = / * = — е^ы при г € Е .

Равенство (19) можно интерпретировать как вырождение на Е бесконечно малых эллипсов с характеристиками (р(г ),9(г)) в бесконечно малые отрезки с углом наклона 9 = 9(г ).

Для всякого г € Е обозначим через р = р(г) (0 <  р < ^) — угол между касательной к Е в точке г € Е и положительным направлением оси 0x 1 . Тогда 9г = | ^г | е^{г( р} (²^ — касательный вектор к Е в точке г. При этом из условия (17) следует, что р = 9, а из условия (18), что р = 9. Это означает, что в случае (17) упомянутые отрезки направлены трансверсально к Е, а в случае (18) — по касательной (см. рисунок).

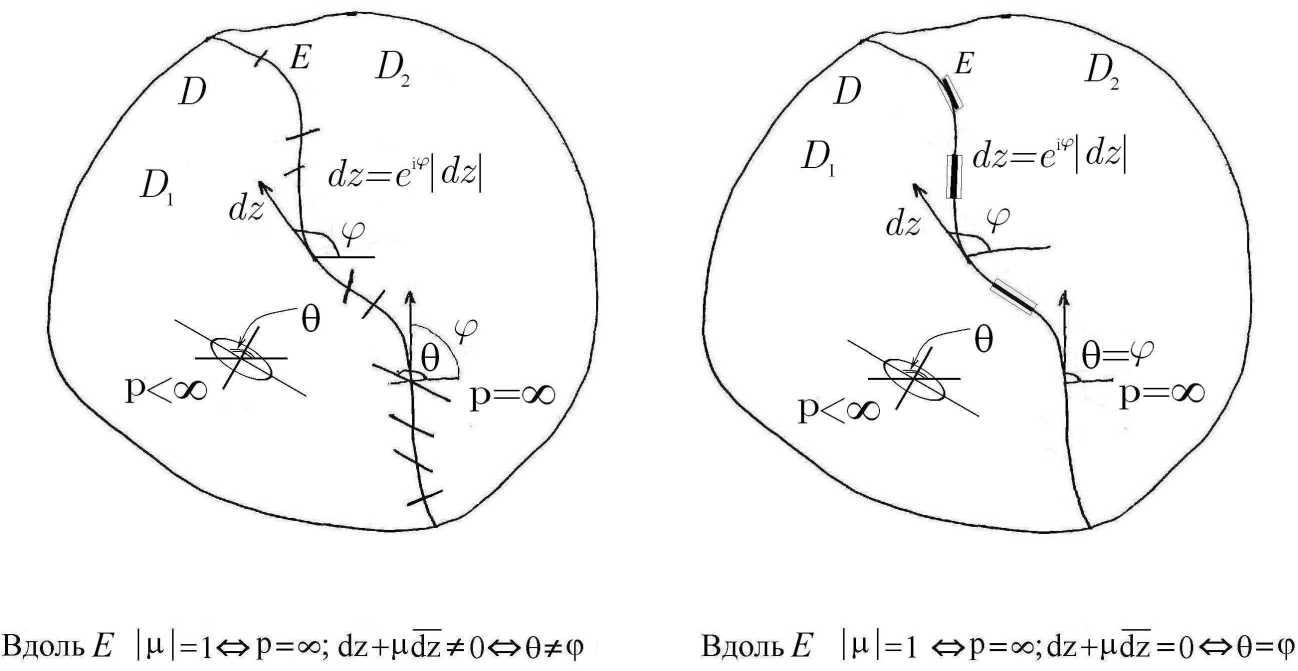
Случаи условий (17) и (18)

Приведем примеры /(г ), иллюстрирующие теоремы 1 и 2.

Случай теоремы 1. Пусть D — односвязная область в C и Н(г ) € C ⁽²⁾ (D) — произвольная функция, такая, что V H(г) = 0 всюду в D. Пусть линия уровня Е = = { г : Н(г ) = 0 } разбивает D на односвязные подобласти D 1 = { г : Н(г ) < 0 } и D 2 = { г : Н(г ) > 0 } .

Положим р(г ) = arg( V H(г)). Зададим произвольно измеримую функцию М(г ) такую, что 0 < m 1 < | М(г) | <  m ₂ (m 1 , m ₂ = const) и непрерывную функцию 5 (t) (5(t) > 0 при t = 0, 5(0) = 0).

Возьмем в качестве /(г) функцию

/(г) = (1 + М (г)5(Н)) е ²⁽^ ^{г )+} 4 > ⁸ = г(1 + М (г)5(Н)) =.

VH

Векторное поле ег^ VH трансверсально VH. В некоторой окрестности 0(Е) существуют функции А(г) > 0 и Z(г) € C(1) (0(Е)) такие, что VZ = А(г) ег^ VH. (Эта функция А(г) есть интегрирующий множитель 1-формы ш = (V2/2) ((Н.1 — Н^)dxi + (Н^ + Н.2)dx2).)

Тогда

v z ц — = v z

ХИ1         VH г = + гM (z)5(H) = vh        vh

-

. vh

г

vh

= | M (z) | ² 5 ² (H)

и левая часть (9) оценивается следующим образом:

IM (z)I5²(H )

vz

ц — ==

vz

+

IM (z ) |

<\M (z) | +

| M (z) |

< m 2 + —. m i

Очевидно, условия теоремы 1 выполняются c К (z) = m ₂ + M = const.

Случай теоремы 2. Пусть D — односвязная область в C. Зададим в ней пару функций Н(z) G C ⁽¹⁾ (D) так, чтобы VH(z ) = 0 всюду в D и линия уровня Е = = {z : Н(z) = 0 } разбивала D на односвязные подобласти D ₁ = {z : Н (z) < 0 } и D 2 = {z : Н (z) > 0 } .

Функцию Z (z) G C ⁽¹⁾ (O(E)) выберем так, чтобы градиент VZ (z) был всюду транс-версален градиенту VH (z), причем l^’^ >  0. (Которую, в частности, можно построить как и в предыдущем случае.)

Зададим произвольно измеримую функцию М (z) такую, что 0 < m ₁ < | М(z) | <  m ₂ (m ₁ , m ₂ — постоянные); непрерывную функцию 5(t) (5(t) >  0 при t = 0, 5(0) = 0), для которой может быть определена функция F 1 .

Положим

ц(z) = (1 + М(z)5(H))e^{M z ) i} .

Тогда имеем

ц

-

vh vh

v h + M _Шн ) v h v h        v h

-

vh vh

| M (z) | ² 5 ² (H),

и левая часть в (11) оценивается следующим образом:

| M (z) | 5 ² (H)

Ц — ^=^=   + । л —rr <  IM (z) | + .   ,—-г <  m₂ + — .

^M VH |M(z) | - ^{1 V Л} IM(z )| -    ² m 1

Тем самым условия теоремы 2 выполняются c К(z) = m ₂ + М = const.

Явно указанным примером пары функций Н (z), Z (z), подходящей как для описанной ситуации случая теоремы 1, так и случая теоремы 2, может служить пара функций

Н (z)=^^ — 1, Z (z)=^^ + |(^2 — ж2), с областью D = {(ж,^) : ж > 0, у > 0} и кривой Е = {(ж,^) : у = 1/ж}.

3.    Геометрические следствия теорем 1, 2

Далее расстояние dist(z,E) от точки z G D до множества Е С Е мы будем рассматривать как функцию z. Желая подчеркнуть это, а также для уменьшения размера формул, мы будем использовать обозначение d g (z), полагая d g (z) = dist(z,E).

При выполнении условия (17) и дополнительных условиях гладкости на кривую E в работах Сребро и Якубова [13, теорема 1.1] была установлена локальная теорема существования и единственности гомеоморфных решений вырождающихся уравнений Бельтрами, записанная в геометрических терминах. Следующая теорема 3 является специальной версией упомянутого результата. Наша цель состоит в том, чтобы показать возможность ее вывода из теоремы 1.

Теорема 3. Пусть D с C — односвязная область, Е с D — кривая класса C ⁽³⁾ , делящая область D на односвязные подобласти D 1 , D 2 , ив D задано уравнение Бельтрами (1). Предположим, что функция p(z) представима в виде

^ = (1 + M(z^p(dE (z))^2),(21)

где: 1) функция p(t) непрерывна на [0, +то), причем p(0) = 0 и p(t) > 0 при t = 0; 2) функция 6(z) G C(1)(D) такова, что всюду на Е dz + e2i6(z) dZ = 0,(22)

при dz , направленном по касательной к Е ; 3) комплекснозначная функция M (z) измерима и п.в. в D

• — < |ReM(z)| < R, |ImM(z)| < R (R = const).(23)

R

Тогда в некоторой окрестности О (Е ) существует решение с особенностью Е уравнения, ассоциированного с (1) .

Доказательство. Положим M 1 (z) = Re M (z), M ₂ (z) = Im M (z).

Пусть s (a < s < 6) — ориентированный натуральный параметр (отсчитываемый от фиксированной точки z0 G Е), заданный на Е, и пусть z = z(s) = £1(s) + z£2(s) — соответствующая натуральная параметризация кривой Е.

Через | • | , {• , •) — будем обозначать стандартные евклидову норму и скалярное произведение в C = R ² , а комплексные числа рассматривать как векторы.

Пусть и (s) = z ‘ (s) — единичное векторное поле, касательное к Е , k(s) = | z ‘‘ (s) | — кривизна кривой Е в точке z(s), n(s) = — £ 2 ( ^s ) + ^х ' 1 (s) — единичное нормальное поле.

Пусть точка z — фиксирована. Рассмотрим функцию

• ^(s) = | z — z(s) | = У(Х 1 — £ 1 (s)) ² + (^ 2 — ^(s)) ² .

С учетом формул Френе и ‘ (s) = k(s)n(s),   ^(s) = — k(s)u (s),

имеем

, ‘( х _ (U ( s ) ,z — z ( s ) ) h ( s )             | z — z(s) |      , ‘‘     _ ((k n( s ), z — z ( s ) ) — | и ( s ) | 2 ) |z — z ( s ) | 2 + (u ( s ), z — z ( s ) y2 h ( s )                                            | z — z(s) | 3                                    .

Отсюда видно, что если z — z(s ₀ ) ± u(s ₀ ), то есть точка z лежит на нормали к Е , проведенной через точку z(s ₀ ), то ^k ‘ (s ₀ ) = 0. При этом

‘‘         1 — (k(s0)n(s0), z — z(s0))     1 ± k(s0)|z — z(s0)| (s0)=            |z — z(so)|            =       |z — z(so)|      ’ где знак «+» или «—» берется в зависимости от того, одинаково или противоположно направлены коллинеарные векторы г — Z(s0) и n(s0), или, иначе говоря, в какой из подобластей D1 или D2 лежит г.

Тогда hn(s0) > 0, если \г — Z(s0)\ < ^^)| и г — Z(s0)±z/(so). Таким образом, указанное s0 является точкой локального минимума функции h(s) и, тем самым, dE (г) = \г — г(в0) |.

Рассмотрим отображение области Q = {(s, t) : \t\ < ]^(1^)]"} из плоскости переменных s,t в плоскость переменных x1,x2, определенное формулой г = г(з) + tn(s).                                      (24)

Данное отображение принадлежит классу C(2), при этом dE (г(s') + tn(s)) = |t \.

Снова, учитывая формулы Френе, имеем

д (x i ,X 2 ) = ^ 1 ^{( s )} - ^t £"^{( s ) —x} 2 ^{( s )} д (s,t)       X 2 (s) + tx”(s) X 1 (s)

x ‘ (s) — tk(s)x ‘ 1 (s) — x 2 (s)

X 2 (s) — tk(s)X ‘₂ (s) X ‘ (s)

= 1 — tk(s) >  0.

По построению данного отображения очевидно, что оно взаимно однозначно отображает некоторую окрестность прямой t = 0 на окрестность кривой Е, причем обратное к нему является отображением класса C ⁽¹⁾ . Пусть Н (x 1 ,x ₂ ) = t(x 1 ,x ₂ ) получается выражением t через x ₁ ,x ₂ из системы уравнений (24).

Положим 5(t) = p( \ t \ ). Тогда (21) примет вид

^(z) = (1 + М(г )5(Н (г))) e ^{2 i6 ( z )} .                            (25)

Отсюда, вычисляя, получаем

|^(г)|2 = 1 + М*(г)6(Н (г)), где М* (г) = 2М1(г) + \М(г)\25(Н(г)). Далее можно записать

\+(г)\ = 1 + ^/1 + М *(г)5(Н (г)) — 1 = 1 + М (г)5(Н (г)), где

М (г) =

_________ М * (г) _________

1 + 71+ М * (г)8(Н (г)) ^.

С учетом (23), равенства d _E (г) = | Н(г) | и непрерывности 5(t), ясно, что можно выбрать столь малое е > 0, чтобы при d _E (г) < е было выполнено

-^ <\М (г)|<С,  -^ <|М(г)|<С, где С = С(R, е) > 0 — некоторая константа.

Пусть Z(z) — функция класса C ⁽¹⁾ , определенная в окрестности Е уравнением

VZ (z) = X(z)e^,                            (27)

где X(z) >  0 — интегрирующий множитель формы w(z ) = cos 9(z)dx 1 + sin 9(z)dx ₂ .

Тогда имеем

d(H, Z ) = H _X i H _X 2 =

Э(Х 1 ,Х 2 )      ^Z x i ^Z X 2

= X(z)(-H _{X 2} cos 9 + H _{X 1} sin 9) = X ( i V H, e^.      (28)

Hx, ^X 1

H x 2

X cos 9 X sin 9

Далее, в (3) положим dz = iVH, откуда получим iVH + e2^ iVH = 0 ^ -2 e-i6(z) (iVH, ei6(z)) = 0.

Тем самым из (28) вытекает, что на Е

W =о

Э(Ж 1 ,Ж 2 )

а в силу непрерывности якобиана это же неравенство справедливо в некоторой окрестности Е. Можно считать, что ориентация Е и параметризация s согласованы так, что d(H,Z) Э(Х1,Х2^

> 0 .

Тогда отображение J (z) = H (z) + iZ (z) вместе с обратным принадлежит классу C ¹ в некоторой окрестности Е , и значит является локально квазиконформным.

С учетом (25), (26), (27), имеем

M (z )I5 ² (H )

VZ ²_t 1

VZ  ⁺ |m (z) |

1         .~„

|M(z> ² (H) I ^{M ( z}^^{5 ( H ( z ))}l ⁺

1    _ M(z)|2

+ iM(z)i = 1M

Тем самым установлено, что в некоторой окрестности Е выполняются условия теоремы 1, с K(z) = K₀, и, следовательно, уравнение, ассоциированное с уравнением (1), имеет решение с особенностью Е. Теорема доказана.

Случай, когда вдоль дуги Е выполняется условие dz + ^(z)dz = 0, дается следующей теоремой.

Теорема 4. Предположим, что 1) H(z) G C^T(D), VH(z) = 0 в D и Е задано уравнением H(z) = 0; 2) функция ^(z) может быть записана в виде:

^(z) = = + M *(z)p(TH (z)|), V H где функция p(t) непрерывна на [0, +то), причем р(0) = 0 и p(t) > 0 при t = 0 и ^ имеет интегрируемую особенность в нуле и комплекснозначная функция М*(z) измерима в D, причем

Re (^ 'М* (z)) > -^, |М*(z)| < С2 (С1, С₂= const).         (30)

v Vа (z)       /    ci

Тогда в некоторой окрестности О(Е) существует решение с особенностью Е уравнения, ассоциированного с (1).

Доказательство. Положим 0(z) = arg(VH(z)), тогда VH(z) = \VH(z) | e¹^ и _e^) = VH

VH

Тогда (29) перепишем более кратко

^(z) =e²<^z)+М *(z)p(|H (z)|).

Так как dz = iVH направлен по касательной к Е, из (29) видим, что при H(z) = 0

^(z) = e

2i6(z) = VH

VH

и, значит, dz + e²*^0(z)dz = 0 при z E Е и dz направлен по касательной к Е.

Как и выше зададим Z(z) E C⁽¹⁾(D) так, чтобы градиент VZ(z) был всюду транс-версален градиенту VH(z), причем da^D)) > 0.

Имеем

Hz) |²= 1 + 2Re (e^-2i6М*)p + |М* |²p².

Откуда

Ipl = 1 + ^1 + 2Re (e^-2i6М*)p + |М*|²p²-1 = 1

2Re(e^-2i6М*) + |М*|²p

—/                               ----p.

V1 + 2Re(e^-2i6М*)p + |М*|²p²+ 1

Замечая, что

Re (e-2i6 М*) = Re (VИм*), с учетом (30), заключаем, что в некоторой окрестности О(Е) |^(z )| = 1 + М (z)5(H(z)), где "1 < |М(z)| < Сз, 5(t) = p(|t|) и С3 — некоторая постоянная. Далее

|М (z)|5²(H)

VH n — =

VH

²        1

⁺|Мх2)Г

|М(z)|^²(H)^{|М (z)5(} )| ⁺|М(z)| <

|М *(z)|²

< |М (z)| ⁺

TW^T < С4 = const.

|М(z)| - ⁴

Тем самым, условия теоремы 2 выполняются c К(z) = С₄, и значит утверждение теоремы справедливо.

Следствие 1. Пусть D с C — односвязная область, Е с D — кривая класса С(3), делящая область D на односвязные подобласти D1, D2. Предположим, что n(z = =Д + м ‘(^e И)'              (31)

VdE (z)

где функция p(t) непрерывна на [0, +то), причем р(0) = 0 и p(t) > 0 при t = 0 и ^ имеет интегрируемую особенность в нуле и комплекснозначная функция М*(z) измерима в D, причем

Re (^^4М*(z)A >   , |М*(z)|< С2 (Ci,C₂ = const).

V V dE (z)       / Ci

Тогда в некоторой окрестности О(Е) существует решение с особенностью Е уравнения, ассоциированного с (1).

Замечание 5. Пример Е = {ж₂ = 0} показывает, что d_E(z) = |х₂| и Vd_E(z) в точках Е неопределен. Но в случае, когда Е есть кривая класса C⁽³⁾, как было видно из доказательства теоремы 3, функция Н(z) = ±d_E(z), где «+» выбирается в одной из областей Dj, г = 1, 2, а «—» — в другой и Н(z) = 0 на Е является функцией класса С⁽¹⁾(О(Е)). Поэтому функция

VdE (z) = VH (z)

VdE (z) = VH (z)

будет по непрерывности продолжаться на Е.

Доказательство. Вытекает из сделанного замечания при выборе указанной Н(z).