Уравнения для описания пространственно-временной эволюции предельно-коротких импульсов

В скалярном приближении компоненты напряженностей полей светового импульса удовлетворяют волновому уравнению, наиболее корректно описывающему распространение ПКИ в вакууме [5, 6, 7]

E (x, z, to ) = g (® )x

x

to                 Г              /-------

J g 2 ⁽ X ) exp i z x + iz^® 2/.

-to

где

c ²

X ² d z

1 to

g ( ® ) = V Ы t ) exp [ i ® t ] dt                  (4)

2п,

- частотный спектр входного импульса,

1 ^to

g 2 (z ) = — [ф(u )exp[- izu du              (5)

2п

-to

- угловой спектр входного импульса.

Функции частотного и углового спектров являются куполообразными, из-за конечности импульсов во времени и ограниченности в поперечном сечении. Основные энергонесущие частоты сосредоточены в диапазоне ® e [ ® ₀ - 1/ T ; ® ₀ + 1 T ] и X e [ - 1 a ₀ ; 1 a ₀ ] , где T - полудлительность импуль-

са, a ₀ - характерный поперечный размер первоначального импульса. Учитывая данные свойства, можно разложить корень

f =

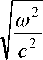
z

в ряд. Популярно и часто используется разложение по формуле Эйлера [5,6]:

®_Z f ~ f 1 = c  2®

(6.1)

Реже применяют разложение (6) в ряд Тейлора, как функцию двух переменных ® и z [7]:

2         2

г г - ® z ®z

J ~ J 2 =+

^С К 2 к₀c

(6.2)

д ² E д ² E 1 д ² E а Х^z С? 1?

Данные разложения справедливы для расстояний, на которых набег фазы от неучтенного члена разложения много меньше п . Для (6.1)

Зададим во входной плоскости поле в виде

E (x, z = 0, t ) = ф (x )y (t)                            (2)

⁰ ^ ^z Э

<<

8 п® ³ a 4 c ³

(7.1)

Для (6.2)

Решение будем искать с помощью метода Фурье. Частотный спектр искомого поля на расстоянии z определяется по формуле

0 <  z_T

8 n k ₀ ³ a 4 c ² T ^-c ² T ² + 4 a 0

(7.2)

Как можно заметить, для длинных импульсов, когда cT >> 2a0, формула (7.2) переходит в (7.1), которая хорошо известна как условие применимости метода параболического приближения [8]. Рассмотрим накладываемые ограничения для случая T = 5, a0 = 100: zЭ << 6.2-1011, zT << 108. Получаем, что разложение Эйлера работает в большем диапазоне расстояний, по сравнению с разложением Тейлора. Т.е. применение разложения Эйлера для дальней зо- ны, наиболее интересной для традиционной оптики [7], является более предпочтительным.

Сравним точность разложения (6) в ряд (6.1) и (6.2). В таблице приведены результаты сравнения (6.1) и (6.2) по критерию s i = max| ( f i - f )/ f в диапазоне энергонесущих значений to и х . Я ₀, T ₀ -длина волны и период несущей частоты.

Сравнение разложения (6) в ряд Эйлера и Тейлора

	a 0 = 100 A 0		a 0 = 500 A 0		a 0 = 1000 A 0
	S 1 , 10 - 11	s 2 , 10 - 11	S 1 , 10 - 1 4	s 2 , 10 - 14	S 1 , 10 - 15	s 2 , 10 - 15
T = 1 T 0	6	105	9.5	4.4 - 10 6	6	1.1 - 10 7
T = 5 T 0	1.6	2.3 - 103	2.7	9.4 - 104	1.6	2.34 - 105
T = 10 T 0	1.5	5.5 - 102	2.3	2.2 - 10 4	1.5	5.5 - 104
T = 20 T 0	1.4	1.3 - 102	2.2	5 - 103	1.4	1.3 - 104
T = 200 T 0	1.3	2.6	2.1	5.4 - 10	1.4	1.3 - 102

Из данных таблицы видно, что с увеличением длительности и ширины импульса точность обоих разложений растет (это обусловлено более узким частотным и угловым спектром). Формула (6.1) более точно аппроксимирует (6), чем (6.2) и это объясняет различие в допустимом диапазоне расстояний при разложении Эйлера (6.1) и Тейлора (6.2). Из представленных данных можно сделать вывод: оба подхода применимы для описания поля ПКИ в ближней зоне, что может быть использовано при исследовании ввода излучения ПКИ в волокно и в интегральной оптике.

После подстановки (5) и (6.1) в (3) и интегрирования по х , получаем:

Е(х, z, to) = J—ig(to)exp izto x \ zA         _ c _

to

x J ф(u)exp

-to

i to (x - u )2

c   2 z

(8.1)

A = 1-- to .

2 ck 0

Если g ( to ) отлична от нуля в малой окрестности to ₀, т.е. импульс достаточно длинный, то (8.2) переходит в (8.1). Интегральное уравнение (8.1) аналогично применению дифракционного интеграла в приближении Френеля для определенной спектральной компоненты. Это является следствием того факта, что функция частотного спектра удовлетворяет уравнению Гельмгольца, применяя к нему теорему Грина, проводя все рассуждения аналогично [9], получим дифракционный интеграл для частотного спектра g ( to ) в виде (8.1).

Подставляя (6.2) в (3) и интегрируя по d to , переходим к временному описанию эволюции импульса

du

E ^{( х} , z , t ) =    J g 2 ⁽ х )/ t

G ( x , z , t )          _

z

z 1 ₊ ^X

I 2k02)

x

c

Подставляя (5) и (6.2) в (3) и интегрируя по х , получаем:

„ „ I ■         ■ Z 2

x expl ixx -1 — X l К 0

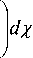
(8.3)

где

E ( x , z , to ) = J---—

^{4     7} \2 z A A

g ^{( to ) exp} iz ^to X

to

x J ф(u)exp

-to

i К 0 ( x - u )

z 4 A

(8.2)

du

Пределы интегрирования меняются в зависимости от x, z, t так, чтобы аргумент функции / (. .. ) принимал допустимые значения.

Для практического использования наиболее применимы интегралы (8.1) и (8.3). Выбор конкретного интеграла следует делать в зависимости от вида функций у ( t ) , ф ( x ) и их Фурье образов.

В частности, если ф ( x ) гауссова функция, а y ( t ) = exp ( at + b ) , взятие интеграла (8.3) не составит труда [7] (получим выражения через интеграл вероятности), в то время как работа с интегралом (8.1) представит определенную трудность. Использование интеграла (8.2) не представляется целесообразным ни для каких функций из-за сложной зависимости подынтегрального выражения от ® . Принимая во внимание ограничения накладываемые (7.1) и (7.2), следует сказать, что интегральное уравнение (8.1) описывает пространственно-временную структуру дифрагированного поля ПКИ на больших расстояниях, чем (8.2) и (8.3). Из уравнений (8.1)-(8.3) получаем, что дифракционное поле ПКИ зависит от временной структуры первоначального импульса, чего не наблюдается, или точнее, на что не обращается внимание, для длинных импульсов.

В заключение отметим, что представленные в данной работе уравнения позволяют проводить качественный анализ волновых полей любой природы и допускают обобщение на случай диспергирующих сред. Получение численных результатов планируется в последующих работах.