Уравнения дробного порядка для диффузии и релаксации в фрактальных средах
Автор: Кирчанов В.С.
Журнал: Вестник Пермского университета. Математика. Механика. Информатика @vestnik-psu-mmi
Рубрика: Математика
Статья в выпуске: 2 (33), 2016 года.
Бесплатный доступ
Получено решение дробного уравнения, описывающего аномальную релаксацию и диффузию в изотропном фрактальном пространстве, в виде произведения функции Фокса на функцию Миттаг-Леффлера, обобщающее результат, полученный в работе [7] и более простое, чем в работе [6]. Использовалась дробная производная Римана-Лиувилля с (0
Фрактальное пространство, дробные производные, аномальные диффузия и релаксация
Короткий адрес: https://sciup.org/14730042
IDR: 14730042 | УДК: 530.1, | DOI: 10.17072/1993-0550-2016-2-30-37
Текст научной статьи Уравнения дробного порядка для диффузии и релаксации в фрактальных средах
Целью работы являются два примера на применение дробного исчисления. Это простой модельный пример решения дробного уравнения, описывающего аномальную релаксацию и диффузию во фрактальных[1–5] пространствах и времени, который ранее рассматривался, например, в работах [6, 7].
Вторым примером является квантовый случай, где мы рассматриваем решение обобщенного квантовостатистического уравнения Неймана–Колмогорова для статистического оператора, ранее полученного методом случайных траекторий [8, 9], для фрактальных пространства и времени.
В обоих случаях для контраста сначала рассматриваем уравнение и его решение в целочисленном дифференциальном исчислении и затем его обобщение в дробном исчислении.
-
1. Диффузия и релаксация в классической системе
Рассмотрим классическую задачу Коши для функции
f
(
x,t
)
где переменными являются координаты
x =(x
1
,
x
2
,
x
3
) и время t (0
fxt) = GV 2 f (x.t)-1 f (x,t), (1.1) dt т где G - коэффициент диффузии, V2 = A -оператор Лапласа, τ – время релаксации.
Это уравнение описывает трехмерный нестационарный массообменный процесс при постоянном коэффициенте диффузии. Его фундаментальное решение в трехмерном случае хорошо известно [10]:
f ( x,t ) = 8 1 ( n Gt ) 2 exp <
—
x 2
4 Gt
—
t
- [ . (1.2) т
Обобщение уравнения (1.1), описывающее стохастический перенос во фрактальных пространстве и времени, имеет вид [6]
Da f (x,t ) = G V2е f (x,t) — -1 f (x,t), та
(0< α ≤1), (0< 2β ≤1) (1.3)
с начальным условием f ( x,t = 0 ) = f 0 ( x ) .
Здесь приводится регуляризованная дробная производная Римана–Лиувилля по времени t [7]
Решение уравнения (1.10) – это функция Миттаг-Леффлера (см. приложение, формулу (П1))
Df (x. t )= D0+f (x. t)-7771—г fax) = 1(1 - a) t
F ( k , t ) = F o ( k ) E , .,
ta ^
—
к
T a
,1 . - f f (x. 0) (t - e)-a de r(1 -a)dt Jo л ’
- 1 f > ( x )
r(1 -a) ta
(1.4)
F (k )f н<2£:]>
0 „=0 r(a n +1)
Применяя получаем
(1.12)
обратное Фурье преобразование,
где Γ(1-α) – гамма функция.
Будем искать фундаментальное решение уравнения (1.3). Применим к нему прямое комплексное преобразование Фурье по координате x :
f
—- f e iF ( k . td =
( 2 n ) -f
1 w
f
f
f dke ik F ( k ) £
2 ₽ -
(1.13) n
_-a a n
T t
-w
n = 0
r ( a n + 1 )
f f ( x . t ) e - ikxdx = F ( k . t ) .
-f k = ( ki. k 2. kз).(1.5)
F x [ D o “+ f ( x , t ) ] = D o “+ F ( k , t ) .
[V2е f (x,t )]=(- ik Г F (k,t) ].(1.6)
где (- ik)2e = |k|2₽ exp(— inP sign k).(1.7)
F [ f (t)] =
(2n)
Рассмотрим частные случаи формулы (1.13).
а) Если коэффициент диффузии G = 0, возникает чистая аномальная релаксация, описываемая уравнением
Dt f (x,t )=- -1 f (x,t) Ta
(1.14)
Радиальная часть дробного лапласиана может быть представлена виде [1]
c начальным условием f ( x,t = 0 ) = f 0 ( x ) .
Решением уравнения (1.14) является функция Миттаг-Леффлера, которая играет роль экспоненциальной функции в дробном
исчислении
V 2 е =
1 d e ( „ - 1 5 е ^
rn - 1 d r e [ r d r e ?
(1.8)
f ( x , t ) = f ) ( x ) E a .1
t
к
T
a
где радиальная производная является дробной производной Римана–Лиувиллля по радиальной переменной:
( F^n
f1 (x^FFFi -<
n=01 (an + 1) к T 7
(1.15)
£f ( rt ^fol r i f ( r't ) r - rrdr’ .
(0 ≤ r), (0< β ≤1), (1.9) что соответствует случаю диффузии в изотропной фрактальной среде.
Подставляя (6–9) в (3) получаем уравнение для Фурье трансформы:
DF ( k,‘ ) =-F kF 1 k,t ) .
с начальным условием F ( k, 0 ) = F o ( k ) . Здесь
Решение проверяется прямой подстановкой выражения (1.15) в уравнение (1.14) и использованием формулы дробного дифференцирования степной функции с произвольным показателем (см. П5).
Функцию Миттаг-Леффлера также можно выразить через функцию Фокса [11], представляемую в виде интеграла Меллина– Бернса (см. П7–8)
(1.10)
f ( x . t ) = f 0 ( x ) H 12
f a ( 0.1 )
t |
T “ ( 0.1 ) . ( 0. a )
-
' , = G(- ik)2e - —. T a(k) V ’ Ta
(1.11)
1 ТП s )Г(1 - s)z -s 2ni f Г(1 -as)
G- i f к /
(1.16)
где z = ( t t 1 ) .
Пример 1 t
Если a = 1 , то f ( x, t ) = f 0 ( x ) e T - экспоненциальная релаксация, 1 если a = — , то
2 ,
- - Г t У 1 / 2
f (x,t) = f о (x)(2n)-1/ 2e T ErfcI I ,
(см. П. 4).
б) Если
т~a
=
0
, то получаем из (1.3) уравнение для аномальной диффузии:
D“
f
(
x,t
)
=
G
V
2
е
f
(
x,t
)
. (1.17)
Используя формулу понижения порядка для функции Фокса (П. 11) приходим к окончательному результату:
1
2
,
0
n
H
1
,
2
П 2 |x|n
j
x
2L
2
2
е
t
a
G
I((
1,
a
)
1
(
2 Ф1
’
1
)
(1.22) Решение (1.22) может быть выражено через интеграл Меллина–Бернса в виде
f
(l
x
l,
t
)
=
(2n i)- n n2 |x|n
1
o+
i
да
J ст-i да Г(1 + 05 )
-z 5 ds
.
В работе [6] к этому уравнению после преобразования Фурье по координатам применяют преобразование Лапласа по времени. Мы будем следовать подходу, развитому в работе [7]. Перепишем трансформу Фурье (12) для модуля
k
.
(1.23)
При
P =
1
решение (1.22) уравнения
n (1.17) переходит в формулу, полученную в работе [7].
В случае
F
0
(
k
) =1, т.е. f
0
(
x
)= δ(
x
) можно предложить приближенное решение уравнения (1.3) в виде
“
t G k
F (Ik, t ) = Fo (I k|)ZU4 = r(an +1) (1.18)
F
0
(|
k
|)
H" ta Gk
l ’I
<0“> (
0,a
)
f
(I
x
|.
t
)
^
4-
H
.220
П2 |x|n 111 n
2
2
е
t
a
G
(
2,
₽
)
,
(
1,1
)
x
и применим
n
-мерное обратное Фурье преобразование для радиальной функции (формулу Бохнера) (cм. П. 6):
E
a
,1
Г t“У “ V T 7 n
2ттУ2
”
П
f (Ix , t )= n 2 Jp 2 Jn /P x|)X
(
2
n
)
n|
x|
2
-
1
(1.19)
(1.24)
Оценки при
n
=
1
,
a = в
,
приводят к форму-
ле [6].
f
(
x,t
)
H
M
Gt
a|
p|
2
е
|
<04
4 d
p
.
1,2 L 11
(
0,1
)
,
(
0,
a
)
J 1
Gt
12
exp
<
(1.25) После применения формулы интегрирования (П.9), выражение становится следующим: 2. Диффузия и релаксация в квантовой системе f (lxl, t) =
2
2
n
-
2
n
+
2
(
2
n
)
n
/2|
x
T
x
T
1,2 3,2
Gt
a
r 2 Г I lxl | (1.20) Ранее в теории магнитной релаксации методом случайных траекторий для спиновой подсистемы отделенной от решетки было по-
(
T,
₽
)
(
0,1
) (
0,1
)
(
0,1
)
,
(
0,
a)
,
Применяя формулу симметрии (П. 10) получаем выражение
f
(I
x
■
t
)
=
4-
H
2,3
π
2
xn
x
2
β
2
2
β
t
α
G
(
1,1
) (
1,
a
)
(
n,
в
),
(
1,1
)
,
(
1,1
)
(1.21)
лучено точное уравнение для неполного среднего матрицы плотности <ρ> [8]
^l^^
xt
)
=
(
-
iL
(
x
,
s
)
+
L
x
(
x
,
t
)
)
< p >
(
x
,
t
)
dt v '
(
2.1) где
L
(
x,s
).
..
=
h
-
1
[
h
(
x,s
)
,...
]
- оператор Лиувилля,
ˆs
– спиновая переменная,
х
– классическая переменная,
L
x
–
оператор уравнения Фоккера–Планка (Колмогорова)
i
= T-1
.
В простейшем одномерном случае это уравнение принимает вид [9]
p(
x,t
)
=
E
a
,
1
, a
-
iL
(
x,s
)
t
a
-
t
T
a
p
(
x,
0
)
. (2.7)
3 (
-----—------= —
iL
(
x
,
s
)
< p >
(
x
,
t
)
+
f — к 1 d2 2 .
- +
G
-
(
x,t
)
т
d
x
J
(2.2) Используя подстановку
< р >
(
x,t
)
=
exp
(
-
iL
(
x,s
)
t
)
p
-
(
t
)
(2.3) получаем решение уравнения (2.2) в следующем виде:
< p >
(
x
,
t
)
=
exp
< -
iL
(
x
,
s)
t
-
—
> х l т I
Решение проверяется путем прямого почленного дробного дифференцирования степенной функции с произвольным показателем (см. П.5). Для вычисления матричных элементов полезна формула
E
a
,1
[-
iL
(
x
,
s
)
t
“
]p
(
x
,0
)
=
E
a
1
[-
i
h
-
HI
(
x
,
s
)
t
a
]x
(2.8)
p
(
x
,0
)
E
a
1
[+
i
h
'HI
(
x
,
s)t
a
J
Приближенное решение уравнения (2.5) можно принять в следующем виде
exp
<
“,
. t2
a
L
(
x
,
s')
iG
2
dx2
> х . (2.4)
p(
x,t^ E
a
,
1
I
/“ 1
-
iL
(.
x,s
)
I
“
E
a
1
- T p
(
x,
0
)
.
к т J
exp
<
t
3
--G
f 1 I d
x
J
И0) (2.9) Первый сомножитель дает квантовые негар- Здесь первый сомножитель – затухающие резонансные осцилляции, второй сомножитель – шумовые осцилляции, третий сомножитель – диффузионное затухание, содержащее квадрат оператора Лиувилля. Подробности в работе [9]. Наличие осцилляционного члена в уравнении (2.1) отличает диффузию в квантовом случае от классического случая (1.1). Для квантовой спиновой частицы, совершающей случайные блуждания по фрактальному пространству и задерживающейся в ловушках, можно предложить уравнение, обобщающее (2.1).
монические осцилляции, которые мы назовем
миттаг-леффлеровские
осцилляции, второй – аномальную релаксацию.
б). Если положить
T
-a
=
0
, то получа-
ется следующее уравнение: D“p( x, t) f 1- iL(x, s)- —+ G к т
a
2
₽
Л a
x
^,
p
(
x
,
t
)
,
(0< α ≤1), (0< 2β ≤1). (2.5) Рассмотрим частные случаи уравнения (2.5).
а) Пусть
G
= 0, тогда уравнение (2.2) становится следующим:
a“ x 1 1 z л drp(x■ t1 l(l .,,Fp(x■ t)= (26) -iL(x, s)p( x, t )-^ x, t) Его решением согласно (1.15) является функция Миттаг-Леффлера
- а
а
2
₽
Dt“p( x, t) = - iL (x,s )p( x, t) + G —re p(x,t).
d
x
e
(2.10) Применим подстановку
p
(
x
,
t
)
=
E
„
,1
[-
iL
(
x
,
s
)
t
a
] p
*
(
t
)
, (2.11) тогда для вычисления дробной производной от статистического оператора будем использовать обобщенную формулу Лейбница для дробного дифференцирования произведения двух функций с остаточным членом (П.13) с
n
=2.
D
“
p
(
x, t
)
=
D
“
[
E
a
,
1
(
-
iL
(
x, f
)
t
“
)
p
*
(
t
)
]
-
D
“
(
u
•
v
)
,
(2.12) где
D
“
(
u
•
v
)
=
D“[E
a
1
(
-
iL
(
x
,
s
)
i
“
)
] -p
-
(
t
)
+
DD
1
'
[
E
.
,1
(
-
iL
(
x
.
s
)
I
“Я^
+
R
2
(2.13) Поскольку функция Миттаг-Леффлера является решением уравнения (1.14), то справедливо выражение
D
“
E
a
,
1
(-
iL
(
x, S
)
t
“
)
=
-
iL
(
x, s
)
E
a
,
1
(-
iL
(
x, S)1
“
)
.
(2.14) Остаточный член согласно формуле (П.13) принимает вид
R
2
=
R
1
_ Г( a)J E. ,1 (- iL (x,s■'''Sp'(e) (t -0)a
d
0
,
D 0+-1 E-д [- iL (X, s) t a] = d' D _j y[-iL (x,s) ta] k 51a 0+z Г (ak +1)
R
=-
(2.15)
+
0
]
0
■
1( a)
0
(
t
- 0)
w
z
k
=
0
[-iL (x, s)]k da Г 1 Г (ak +1) dt “^Г(1)
J
0
a
k
d
0 =
. (2.21)
t (2.16)
Oценки остаточных членов
R
1
и
R
2
требуют отдельного рассмотрения.
w
z
k
=
0
[—iL (x, s)]k d
। a
Г
t
a
k
+
1
Г (ak +1) 51a ^ ak +17 Для вычисления дробной второй производной по координате используем формулу почленного дробного дифференцирования (П.12):
p
(
x,t
)
=
1
[
-
iL
(
x,s
)
t
a
]
‘
.
a
x
e R
’ z
г
(
-
k
+
1
)
a
xL v 7 J
Z
[-
iL
(
x
,
S
)
t
a
]
k
t
^a
k
=
0
r
(
a
k
+
2
-a
)
Решение уравнения (2.21) относительно
p
*
(
t
)
=
(2.17)
G
f exp i_
a{
2₽ r t E J-iL(x,s)0a! G fax2L‘01L__J
DZ' E„
[-
iL
(
x
,
s
)
0
“
]
d 0
*
. (2.22)
ГР
о
Предположим степенную зависимость оператора Лиувилля от координаты Если обозначим
L
(
x,s
)
=
bx
n
•
L
(
s
)
, где
n
=1, 2,…,
b –
постоянная.
z = -iL(tyxn0a , b = ,r(1 + nk) ', k r(1 + nk - 2p) Тогда, используя повторно почленного дифференцирования и формулу формулу k r(a k + 2 -a) (2.23)
(П.5) для дробного дифференцирования координате
х,
получаем
по и подставим (2.19) и (2.21) в (2.22), то получим показатель экспоненты в виде отношения двух рядов
d
2
p Z . X
a[-
L
(
s
)
t
a
bx
n
]
k
^'
xE
,1
(-
iL
(
x
■
s
)
t
“)
= zr
(
a
k
+
1
)
X
(2.19)
Г
(
1
+
nk
)
1
Г
(
1
+
nk
-
2
p
)
x^
p*( t ) = exp < Gt ax” J w z bkZk
—k^----
d
0
w
E
k
n1-a
a
k
z
0
k
=
0
k.(2.24)
Подставляя выражения (2.13–15), (2.19) в (2.10) и опуская R
2
, получаем уравнение для
P
*
(
t
)
:
Применим формулу деления рядов получим выражение для
p
*
(
t
)
в виде
(П.15), aD„Г E„ [-iL (x, s) t-^^Pit) = L J d t G dxf E„ [- iL (x ■ s) t “}P*( t) (2.20) p*( t )=exp < Gr (2-a) ax2p w X
kt
na
k
zck-[- iL (s) bxn ] J тагd 0
^
k
=
0 0
0
*
ГР
0
Вычислим первый сомножитель (2.20), используя формулы (П.12) и (П.5) в (2.25) После интеграции по времени получаем выражение для решения уравнения (2.20) в виде
p
’
(
t
)
_
exp
<
Gt
a
r
(
2
-a
)
a
2
x
23
TO ZCk k=0
[-
iL
(
s
)
bx
n
t
“
]
k
к
+
1
*
ГР
О
. (2.26) Подставляя (2.26) в (2.11), и удерживая первые три члена в сумме, получаем окончательно следующее приближенное решение обобщенного уравнения (2.5):
p
(
x
,
t
)
=
E
a
1
1^-
it
a
L
(
s
)
bx
n
'x
(1.24) для аномальной диффузии и релаксации, обобщающая результат работы [7], и более простая, чем в работе [6]. В квантовом случае получен новый результат (2.27) при решении обобщенного квантовостатистического уравнения Неймана–Колмогорова для неполного релевантного статистического оператора, содержащий негармонические осцилляции, аномальную релаксацию и аномальное диффузионное затухание. Для удобства применения составлено математическое приложение, см. также приложение в обзоре [2].
E
a
,1
( - к t" '
dexp
1
t
a
G
Г
(
2
-a
)
a
2
Г
(
1
-
2
₽
)
Г x Приложение
exp
<
it
2 a
L
(
s
)
bx
n
G
Г
(
2
-a
)
2
a
x
e
c
1
Г x
exp
<
t
3a
L
2 (
s
)
b2 x2 nG
Г
(
2
-a
)
3
a
2
x
23
C2 Г -P*(0) . ( 0< α ≤1), ( 0< 2β ≤1) . (2.27)
Коэффициенты
с
0
,
с
1
,
с
2
принимают вид
_ 1C0 = r(1 - 2p), c _ r(1 + n) Г(2-a)
1
r
(
1
+
n
-
2
p
)
r
(
2
)
r
(
1
-
2
p
)
,
c
_
Г
(
1
+
2
n
)
Г
(
2
-a
)
c
r
(
2
-a
)
c
2
Г
(
1
+
2
n
-P
)
Г
(
2
)
1
г
(
2
+ a
)
°'
Если теперь сравнить решение (2.27) квантового дробного уравнения (2.5) с решением (2.4) квантового целочисленного уравнения (2.2), то видно, что первый сомножитель соответствует квантовым негармоническим (миттаг-леффлеровским) осцилляциям, второй сомножитель – аномальной релаксации, третий сомножитель – экспоненциально возрастает, четвертый – содержит шумовые осцилляции, пятый сомножитель – это диффузионное затухание, содержащее квадрат оператора Лиувилля. Остальные члены в решении (2.27) требуют отдельного рассмотрения.
1 .Функция Миттаг-Леффлера [11] c. 221:
to
к
2 .Функция типа Миттаг-Леффлера [11] с. 224, [13], с. 117:
E
a
(
z
)
=
E
a J
(
z
)
=
Z
TTz—TX
' (П-1)
к
_
°
r
(
a
к
+
1
)
Ea
e(
z
)_y ,
z
A • (П.2)
aM ’ £°
r
(
a
к
+ p) 1
В книге [13] и справочнике [12] другое обозначение индексов. 2 7 <7 где TO . z 5. Дробная производная Римана– Лиувилля степенной функции с произвольным показателем [4], c. 140, ф. 1: a D °+(t ’)'y (t 1
Г
(
1
+ ц
)
t
и-й
Г
(
1
+ ц - a
)
(П.5)
6. Формула Бохнера для радиальной функции (зависящей от |
x
| =
r
) [4] с. 358:
Заключение Следует сказать, что из-за недостатка места не изучено асимптотическое поведение полученных результатов. Тем не менее, полученные результаты достаточно интересны: в классическом случае получена формула TO
.f
(I
x
.
t
)= , .
.
J
e F
(I
к\
•
t
)* =
(2п) -то n (П.6) (2n)2 TO / An I ,
(
2
n
)
n xp
°
2
-
1
где H
m
,
n p
,
q
. (a
1,
A
)
,...
(
a
p,
A
p
)
z
|
(
b
,
,
B
1
)
,...
(
b
q
,
B
q
)
=---X 2n i rUnn - 1)! J ( t - T 11 u( T ) dT...
..
.
. Г1
Г
(
b
j
+
B
j
S
)l
i
r
(
1
-
a
j
-
A
j
S
)
J j----------,
°-
i
~
П
r(
a
i
+
A
j
s
)
П
r(
1
-
b
j
-
B
j
s
)
j=n+1 (П.7) 8. Выражение функции типа Миттаг-Леффлера через функцию Фокса [12] с. 728: / и Г (o,i)
Ea
»(
-
z
)
=
H
11
z
|( Л,7 . . (П.8)
aM 7 1
,
2
(
0,1
)
,
(
1
-в
,
a
)
...J (t-0' 1 ^(«d 5. T Ia I (1)n-1 ar(k-a) ( k J Г(1 -a)r(k +1) коэффициент. биномиальный
14. Для дробного дифференцирования сложной функции
f
(
g
(
x
))
можно предложить формулу
9. Формула для интегрирования функции Фокса и специальной функции [12] с. 355: .
J
X
a-
1
j
,
(
.
X
)
H
mq
a
x
r
|
r
a
p
,
A
p
]
Г
b
q
■
B
q
]]
^ a-
1
_ 2 mTm
,
n
+
1
= .
a
H
P
+
2,
q
f(g(x, (П.14) 5x 5g 5x где дробная производная функции f (x) по другой функции g(x) определяется формулой [4] с. 249.
Г
b
q
•
B
q
]
(П.9) 10. Формула симметрии функции Фокса [12] с. 628:
m,n
a
p
,
p n,m
1 -
q
,
q
H
r
z
’k^
.
]
]=
H
Г
z
1!-
a
p
,A
P
r 0)
£f
л.
1
dgp a+;gf () r(1 -p) g‘(x) — x---—---₽g'(У) dy dxJ Г g (x)-g (У )f[ )
Однако выражения, полученные по формулам (П.12) и (П.14) для функции
f
(
g
(
x
))
=
E
a
,
1
[
-
L
(
s
)
bxnt
a
]
, совпадают только при
n
= 1.
11. Формула понижения порядка функции Фокса [12] с. 628: 15. Формула для деления функциональ-
m
,
n
H
p
,
q
(
a
1
,
A
1
)
,...
(
a
p
,
A
p
)
z
|
Г
b
q
-
1
,
B
q
-
1
]
,
(
a„ A
1
)
ных рядов:
TTm
,
n
-
1
H
p
-
1,
q
-
1
(
a
2
A
)
,...
(
ap
,
Ap
)
z|
Г
bq
-
1
,
Bq
-
1
]
(П.11) где 12. Формула для почленного дробного дифференцирования ряда [4] с. 215: .
D
a
+
X
f
n
(
x
)
=
n
=
0
J
n .
X
D
,
“+
f,
(
x
)
. (П.12)
n
=
0
J
13. Обобщенное правило Лейбница для дробного дифференцирования двух функций с остаточным членом [4] § 17:
D
+a
(
u, v
)
=
X
n
-
1
к
a I
k=0 v k у
D
a-
k
(
u
)
•
v
(
k
)
+
R
n
, (П.13)
. . X bkZk k akZk k=0 Vk=0
1
.
=
1
X
C
k
Z
k
, (П.15)
a
0
k
=
0
1n cn = b —X cn-kak; c0 =b0; a 0 k=1 a aa c 1 = b1--c 0; c 2 = b 2--c 1--c 0.
a
0
a
0
a
0
16. Формула для вычисления экспоненциального оператора от квадрата оператора Лиувилля (двойного коммутатора) [8]: .
exp
{
-
a
2
L
2
}
=
J
dxexp
{
- n
x2
-. - i 2 Vn • xaL} .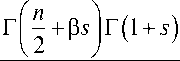
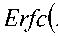
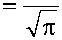
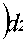
n
-
2
J
F
(
p
,
t
)
P
2
J
n
.(
p
x
|)
d
p
Список литературы Уравнения дробного порядка для диффузии и релаксации в фрактальных средах
- Зеленый Л.М., Милованов A.M. Фрактальная топология и странная кинетика//Успехи физических наук. 2004. Т. 174, № 8. С. 809-852.
- Учайкин В. В. Автомодельная аномальная диффузия и устойчивые законы//Успехи физических наук. 2003. Т. 173, № 8. С. 847-874.
- Нахушее A.M. Дробное исчисление и его применение. М.: Физматлит, 2003. 272 с.
- Самко С.Г., Килбас А.А., Маричее О.И. Интегралы и производные дробного порядка и некоторые их приложения. Минск.: Наука и техника, 1987. 688 с.
- Чукбар К.В. Стохастический перенос и дробные производные//Журнал экспериментальной и теоретической физики. 1995. Т. 108, вып. 5(11). С. 1875-1884.
- Кобелее В.Л., Романов Е.Н., Кобелее Я.Л. и др. Нелинейная релаксация и диффузия в фрактальном пространстве//ДАН. 1998. Т. 361, № 6. С. 755-758.
- Кочубей А.Н. Диффузия дробного порядка//Дифференциальные уравнения. 1990. Т. 26, № 4. С. 660-672.
- Кирчанов B.C. Диффузия в ЯКР//Известия вузов. Физика. 1985. № 6. С. 14-16;
- Кирчанов B.C. Диффузия и релаксация дробного порядка во фрактальных средах в классическом и квантовом случае//Известия вузов. Физика. 2009. Т.52, № 4. С. 15-23.
- Полянин А.Д. Справочник по линейным уравнениям математической физики. М.: Физматлит, 2001. 576 с.
- Бейтман Г. и Эрдейи А. Высшие трансцендентные функции//Эллиптические и автоморфные функции Ламе и Матье. М.: Наука, 1967. Т. 3. С. 221.
- Прудников А.П., Брычков Ю.А., Марычев О.И. Интегралы и ряды. Дополнительные главы. М.: Наука, 1986. 800 с.
- Джрбашян М.М Интегральные преобразования и представления в комплексной области. М.: Наука, 1966. 672 с.


