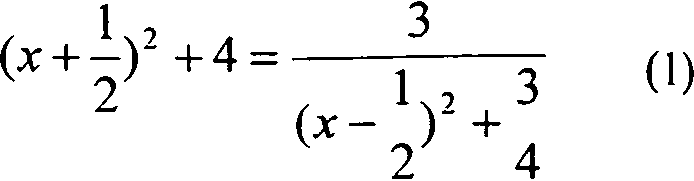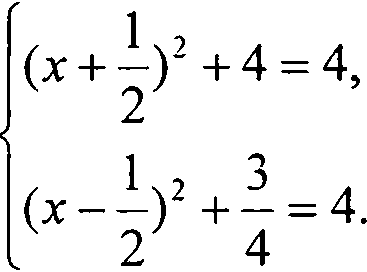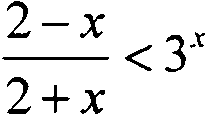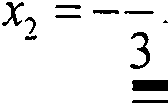Уравнения и неравенства на факультативных занятиях по математике

Для математического образования характерны две традиции. Первая связана с тем, что человек должен уметь пользоваться известными алгоритмами, вторая ориентирована на то, чтобы научить человека думать. Российская традиция всегда основывалась на развитии интеллекта. Одна из целей математического образования на современном этапе - не дать угаснуть этой замечательной традиции.

Респонденты профессора В.М. Тихомирова из США, Канады, некоторых европейских стран при выборе вариантов ответа на вопрос «В чем состоит цель математического образования: подготовка в вуз, подготовка к будущей профессии, интеллектуальное развитие, формирование мировоззрения, ориентация в окружающем мире, “физкультура” мозга?» предпочтение отдавали «подготовке к будущей профессии».

В России и странах бывшего Советского Союза первое место, причем с большим отрывом, всегда занимало интеллектуальное развитие (Тихомиров В. О некоторых проблемах математического образования // Вести, высш, образования. 2000. № 7. С. 21 - 26). Аналогичные результаты были получены нами и при проведении опроса среди студентов математического и строительного факультетов Мордовского государственного университета им. Н.П. Огарева: 70 % респондентов на первое место поставили интеллектуальное развитие и «физкультуру» мозга. Кроме того, к предложенным в анкете целям математического образования многие студенты-математики добавили «умение нестандартно мыслить и находить другие, лучшие варианты разрешения проблем».

Однако школьный курс математики нацелен преимущественно на решение большого количества стандартных задач, решаемых по определенным алгоритмам. Достичь сформулированных выше целей математического образования с помощью таких задач невозможно. По мнению известного американского методиста и математика Д. Пойа, если преподаватель математики заполнит отведенное ему учебное время натаскиванием учащихся в шаблонных упражнениях, он убьет их интерес, затормозит их умственное развитие и упустит свои возможности. Поэтому целесообразно включать как в школьный курс математики, так и, в особенности, на факультативные занятия нестандартные задачи. Мы в течение многих лет разрабатываем системы таких задач для 7-11-х классов. Ниже приведены некоторые материалы по решению нестандартных уравнений и неравенств, которые, как правило, не могут быть непосредственно решены по известному алгоритму. Возникает необходимость поиска решения, что способствует развитию творческого мышления, порождает радость открытия - этот важнейший эмоциональный фактор развивающего обучения, поддерживает интерес учащихся к поиску решения задач.

Нестандартные задачи требуют определенной сообразительности, свободного владения различными разделами математики, высокой логической культуры, а помимо этого - и психологической подготовленности. Нередко бывает, что задача, по существу совсем несложная, но сформулированная несколько необычно, вызывает

непреодолимые трудности. А ее решение требует всего несколько слов.

Приведем примерное распределение занятий факультативного курса «Нестандартные уравнения и неравенства» и фрагменты некоторых факультативов.

1-е занятие. Доклады учащихся по теме «Роль и место уравнений и неравенств».

На первом занятии важно проверить степень подготовленности учащихся к решению уравнений и неравенств, вспомнить базовые понятия по данной теме. Для этого мы используем устные упражнения.

Упражнение 1. Из приведенных ниже утверждений выберите неверные

• а)    Неравенства /(x)>g(x) и /(x)-g(x)> 0 равносильны.

• б)    Неравенства /(x)>g(x) и /’(х)+ а > &Ы+ ^а равносильны для любого числа а.

• в)    Неравенства /(x)>g(x) ^и

• <^М>ag^ равносильны для любого числа а.

  /U) gW г) Неравенства а >а и

• сированного числа из промежутка (1; + co).

JW g(x)

• д)    Неравенства а >а и Дх) > g(x) равносильны для любого фиксированного числа из промежутка (0; 1).

Предложите контрпримеры для неверных суждений.

Ответ: в), д).

Упражнение 2; Равносильны ли следующие неравенства.

• а)    х³< 1 и х< 1;

• б)    Vx-1 <х и х-1<х²;

• в)    л/х ~ 1 — X И X ^— 1 > X ;

х3 — х—1

г) э \ . . ;

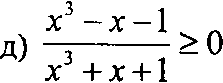
и х6-х2-2х-1>0.

Ответ: а) да, б), в), г), д) нет.

• 2 - 3-е занятия. Использование ОДЗ при решении уравнений и неравенств.

Иногда знание области допустимых значений уравнения или неравенства позволяет доказать, что уравнение или неравенство не имеет решений, а иногда это знание позволяет получить решение непосредственной подстановкой чисел из области допустимых значений.

Пример 1. Решите уравнение:

cos х| = ^- |cos х| + ctgx.

Решение: ОДЗ этого уравнения состоит из всех х, одновременно удовлетворяющих условиям

|cosx| > 0, -|cosx| > 0, х Ф 7т, х е Z , т.е. ОДЗ есть X — ~ + ^? к g Z . Подставляя эти значения х в исходное уравнение, получаем, что его левая и правая части равны 0, а это означает, что все х = — + лк, к е Z, являются его решения-2                          и ми.

Ответ: х = — + тгк, keZ 2

Пример 2. Решите неравенство: JxT7 + V49-x < V?

Решение: ОДЗ неравенства есть все х из промежутка — 7 < х < 49 ■ Разобьем это множество на два промежутка: - 7 < х < О и 0<х<49 Для х из промежутка -7<х<0 имеем

VT+7 > О, V49- х >№ = 41.

Следовательно, на этом промежутке Vx4-7 + 749-х > V? и исходное неравенство не имеет решений.

Пусть х принадлежит промежутку 0<х<49- Тогда  Vx + 7 > V? ^и

749-х > 0 • Следовательно,

77+7 + 749-х > 77

для таких х и на этом промежутке неравенство также не имеет решений.

Ответ: Решений нет.

4 - 5-е занятия. Использование ограниченности функций при решении уравнений и неравенств.

При решении уравнений и неравенств свойство ограниченности функции сверху или снизу на некотором множестве часто играет определяющую роль. Например, если для всех х из некоторого множества М справедливы неравенства

/(х)>Я, g(x)

Заметим, что если роль числа А играет нуль, то в этом случае говорят о сохранении знака функций /(х), g(x) на множестве М.

Если при решении уравнения /(х) = g(x) удается показать, что для всех х из некоторого множества М справедливы неравенства f(x) и g(x) > А , то на множестве М уравнение равносильно системе уравнений

/(х) = A, g(x) = А .

Пример 3. Решите уравнение:

4х2+4х + 17 = —-- х -х + 1

Решение: Перепишем уравнение в виде

Очевидно, что для любых действитель- ных х имеем

/м=гтг^54

Х 2 + 4

Следовательно, уравнение (1) равносильно системе уравнений:

Эта система уравнений решений не имеет, поэтому исходное уравнение также не имеет решений.

Ответ: Решений нет.

Пример 4. Решите неравенство:

Решение: ОДЗ неравенства (2) есть все действительные х, кроме х = - 2. Разобьем ОДЗ на три множества — оо<х<-2,

- 2 < х < 0, 0 < х < +оо и рассмотрим неравенство на каждом из этих промежутков.

Пусть - оо < х < -2 • Для каждого из этих х имеем g(*) = ~---<0. а 24-х

/(х) = У>0.

Следовательно, все эти х являются решениями уравнения.

Пусть — 2 < х < 0. Для каждого из этих х имеем

g(x) = 1 -

2х

24-Х

a f (^) = 3^х< 1. Следовательно, ни одно из этих х не является решением исходного неравенства.

Пусть 0 < х < +оо • Для каждого из этих х имеем

gOO = 1 -

2х

2 + х

/(х) = 3^х > 1. Следовательно, все эти х являются решениями неравенства.

Ответ: -оо<х<-2, 0<х<+оо.

6-е занятие. Семинарское занятие на тему «Прикладные аспекты уравнений и неравенств».

Рекомендуемая литература: Кипнис И.М. Сборник прикладных задач на неравенства. М., 1964.144с.; Шкарин А.Б., Федянов А.М., Сандлер Б.Г. Алгебраические задачи в технике. М., 1962. 116 с.

7-е занятие. Использование монотонности при решении уравнений и неравенств.

Метод обращения к монотонности функции чаще всего применяется в двух случаях. Во-первых, тогда, когда данное уравнение имеет в одной части функцию возрастающую (убывающую), а в другой постоянную. Такое уравнение не может иметь более одного корня. Во-вторых, тогда, когда одна часть уравнения представляет собой возрастающую функцию, а другая -убывающую. Графики таких функций не могут иметь более одной общей точки, а уравнение не может иметь более одного действительного корня.

Пример 5. Решите уравнение:

Vx--2 + V2x-5 = 2.

Решение: Запишем уравнение в виде V^2=2-V2x-5.

Подбором убеждаемся, что х = 3 - корень данного уравнения. Поскольку функция у = 2 - V2x-5 монотонно убываю-щая, а функция у = Vx-2 монотонно возрастающая, то других корней нет.

Ответ: х = 3..

Пример 6. Решите неравенство:

V2-X2 > х3 + х-1.

Решение: ОДЗ неравенства есть все х из промежутка - V2 < х < V2 . Все х из промежутка — V2 < х < О являются решениями исходного неравенства, так как для каждого такого х имеем, что функция /(х) = V^v неотрицательна, а функция g(x) = х3 + х -1 отрицательна.

Рассмотрим исходное неравенство на промежутке (0;V2J- Поскольку функция g(x) непрерывна и строго возрастает на этом промежутке, функция /(х) непрерывна и строго убывает на этом промежутке, то уравнение f(x) = g(x) имеет единственный корень на этом промежутке. Легко видеть, что таким корнем является х = 1.

Для каждого х из промежутка (0; 1) имеем, что /(х) = ^2-х2 >Ь а g(x) = х3 + х — 1 < 1 • Поэтому все х из этого промежутка являются решениями исходного неравенства. Для каждого х из про-межутка (1; V2] имеем, что /(х) = V2-x2 < L а g(x) = х3 + х -1 > 1 Поэтому такие х не удовлетворяют данному неравенству.

Итак, решениями исходного неравенства являются все х из промежутка [-V2; 1)

Ответ: — V2 < х < 1.

8 - 9-е занятия. Использование суперпозиции функций при решении уравнений и неравенств.

Пример 7. Решите уравнение:

(х2 + Зх - 6)2 + 3(х2 + Зх - 6) - 6 = х.

Решение: Обозначим

f(x) = х2 + Зх - 6 , тогда исходное уравнение можно переписать в виде fU\x^)-x- Теперь очевидно, что если х0 - корень уравнения /(х) = х, то х0- и корень уравнения /(/(х)) = х. Корнями уравнения х2+3х-6 = х являются х, = -1 - V?, х2 = -1 + J7 Следовательно, и исходное уравнение имеет эти корни. Переписав уравнение в виде х4 + 6х3 - 28х +12 = О и разделив многочлен х4 + бх3 - 28х +12 на многочлен (^-^Хх-хЦ. получим, что последнее уравнение можно записать в виде

(х2 +2х-б)(х2 + 4х-2) = 0 Следовательно, корнями уравнения наряду с хр х2 являются также корни уравнения х2+4х-2 = 0,т.е. числа х3 = -2 - Тб, х4 = -2 + Vd

Ответ: Х] = -1 - V?, х2 = -1 + V? , х3 = -2 - Vd, х4 = -2 + V6

При проведении этих занятий мы использовали материалы работ И.И. Чучае-ва, С.И. Мещеряковой, Е.Г. Смольяновой и М.Ю. Табачковой (см. например: Математика в школе. 1997. №6; Интеграция образования. 1999. № 2).

10-е занятие. Использование графиков при решении уравнений и неравенств.

Здесь мы особенно широко использовали графики при решении уравнений и неравенств с параметрами, которые, как правило, вызывают большие затруднения у учащихся.

11-е занятие. Итоговое повторение на тему «Функциональный подход к решению уравнений и неравенств».

Упражнение 3. Раскройте идею решения следующих уравнений и неравенств:

• 1)   2^Х+3^Х+4^Х<3,

• 2)    cosx = 1+х⁸,

• 3)    3^х+4" =7,

• 4)   х-2^х=8,

• 5)  р2 + Л J + ^2-ТзУ =2^Х,

• 6)    3^х + 4^х > 5^х,

• 7)    4cos2x-cos4x = 1бх + 3, 8)V 4х +1 — V6 — х — V5 — 2х + Vx + 2 = 2,

• 9)   V4x + 4 + V4x + 12 = 4,

• 10)    х²⁰⁰¹+ 2000 х = 2001,

И) (х4 -4х2 +2)4 -4(х4 -4х2 + 2^ = = х-2,

• 12)    6 + ^6 +... + ^6 + х³ У ...jf⁵ — х,

• 13)  ^9 + V9 + x = х,

• 14)    x³+l = 2V2x-l,

• 15)    (х³+2х-2)⁴ + 2х³+Зх-6 = 0.

72 - 14-е занятия. Классические неравенства и их применение к решению уравнений.

Рекомендуемая литература по теме «Доказательство классических неравенств»: Шлейфер В. Об одной схеме доказательства неравенств // Математика в школе. 1984. № 6. С. 58 - 60.

Учащимся предлагается самостоятельно составить уравнения по данной теме.

75 - 16-е занятия. Различные нетрадиционные методы решения уравнений и неравенств.

• 77-    18-е занятия. Нестандартные по формулировке задачи, связанные с уравнениями и неравенствами.

Пример 8. Выразите свободный член кубического уравнения х3 + ах2 + Ьх + с = 0

^^^^               3, через коэффициенты а и Ь, зная, что корни этого уравнения образуют арифметическую прогрессию.

Решение: Поскольку корни x_v х₂, х₃ уравнения образуют арифметическую прогрессию, то удобно их обозначить так: %, = к - d, х₂ = к, х₃ = к + d В силу этих обозначений находим х, + х₂ + х₃ = Зк , а на основании формулы

Виета имеем х, + х₂ 4- х₃ = -а

Из двух предыдущих равенств следу-

7 -  ° ет, что К — —~ 3

но так как х₂ = к , то

а

Подставив этот корень в данное уравнение, получим

(-|)3+^(-j)2+6(-j) + C = 0.

9аЬ-2а" откуда с = ---—---

9аЬ-2а"

Ответ: с =--------- 27

19-е занятие. Итоговое повторение. Зачет.

Подчеркнем, что экспериментальное апробирование всех разработанных материалов проводилось нами в трех типах школ (естественно-техническом лицее, малой школьной академии и в математических классах школы № 32 г. Саранска).

ПРИМЕНЕНИЕ СИСТЕМЫ MATLAB К РЕШЕНИЮ ЗАДАЧ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ

Сопротивление материалов как одна из важнейших дисциплин играет существенную роль в подготовке инженеров любых специальностей и входит в программу обучения студентов вузов большинства технических факультетов.

На основных принципах сопротивления материалов базируются такие дисциплины, как строительная механика, строительные конструкции, теория машин и механизмов, детали машин. В различных курсах по машиностроительным, механическим,строительным, приборостроительным и другим специальностям также широко используются важнейшие положения сопротивления материалов.

Главной задачей дисциплины является исследование напряженно-деформированного состояния элементов на различных стадиях нагружения внешней нагрузкой. Хорошее усвоение студентами курса сопротивления материалов предполагает не только глубокое изучение теории,но и приобре тение твердых навыков в решении задач и проведении исследований. При этом очень важна визуализация их результатов, что не всегда осуществимо вручную, и требуется развитие методов исследования напряженно-деформированного состояния материалов.

Исследование напряженно-деформированного состояния материалов с помощью методов теории упругости предусматривает решение необходимого количества уравнений механики, с помощью которых могут быть определены тензоры напряжений, перемещений и деформаций. Этими уравнениями являются:

• а)    дифференциальные уравнения равновесия (Новье), устанавливающие общие условия равновесия внутренних усилий в элементах;

• б)    статические условия на поверхности тела (граничные условия), используемые для определения постоянных интегрирования, появляющихся при интегрировании уравнений (а);